Analiza matematyczna 2/Wykład 3: Norma. Iloczyn skalarny: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| (Nie pokazano 26 wersji utworzonych przez 3 użytkowników) | |||
| Linia 21: | Linia 21: | ||
Funkcję tę nazwiemy normą. | Funkcję tę nazwiemy normą. | ||
Okaże się | Okaże się | ||
(zgodnie z intuicją, jak dla przypadku płaszczyzny <math> | (zgodnie z intuicją, jak dla przypadku płaszczyzny <math>\mathbb{R}^2</math>), | ||
że jeśli umiemy zmierzyć długość wektorów | że jeśli umiemy zmierzyć długość wektorów | ||
przestrzeni wektorowej <math> | przestrzeni wektorowej <math>X</math>, | ||
to możemy także mierzyć odległość między punktami | to możemy także mierzyć odległość między punktami | ||
zbioru <math> | zbioru <math>X</math>. | ||
Pojęcie normy jest szczególnie przydatne w przestrzeniach | Pojęcie normy jest szczególnie przydatne w przestrzeniach | ||
| Linia 34: | Linia 34: | ||
Wprowadźmy formalną definicję | Wprowadźmy formalną definicję | ||
(wektor zerowy przestrzeni wektorowej <math> | (wektor zerowy przestrzeni wektorowej <math>X</math> będziemy oznaczać przez <math>\Theta</math>). | ||
{{definicja|3.1.|| | {{definicja|3.1.|| | ||
Niech <math> | Niech <math>X</math> będzie przestrzenią wektorową nad ciałem <math>K</math> | ||
(<math> | (<math>K=\mathbb{R}</math> lub <math>K=\mathbb{C}</math>).<br> | ||
Odwzorowanie | Odwzorowanie | ||
<math> | <math>\|\cdot\|\colon X\longrightarrow\mathbb{R}_+</math> nazywamy normą w <math>X</math>, jeśli:<br> | ||
'''(1)''' | '''(1)''' | ||
<math> | <math>\forall x\in X: | ||
\|x\|=0\ \Longleftrightarrow\ x=\Theta</math>;<br> | \|x\|=0\ \Longleftrightarrow\ x=\Theta</math>;<br> | ||
'''(2)''' | '''(2)''' | ||
<math> | <math>\forall x\in X,\ \ \lambda\in K: | ||
\|\lambda x\|=|\lambda|\cdot\|x\|</math> | \|\lambda x\|=|\lambda|\cdot\|x\|</math> | ||
(jednorodność);<br> | (jednorodność);<br> | ||
'''(3)''' | '''(3)''' | ||
<math> | <math>\forall x,y\in X: | ||
\|x+y\|\le\|x\|+\|y\|</math> | \|x+y\|\le\|x\|+\|y\|</math> | ||
(subaddytywność).<br> | (subaddytywność).<br> | ||
Parę <math> | Parę <math>(X,\|\cdot\|)</math> nazywamy | ||
'''''przestrzenią unormowaną'''''. | '''''przestrzenią unormowaną'''''. | ||
}} | }} | ||
| Linia 71: | Linia 71: | ||
W przestrzeni wektorowej | W przestrzeni wektorowej | ||
<math> | <math>\mathbb{R}^N</math> nad <math>\mathbb{R}</math> możemy wprowadzić następujące | ||
normy:<br> | normy:<br> | ||
<math> | <math>\|x\|_{2} | ||
\stackrel{df}{=} | \stackrel{df}{=} | ||
\sqrt{\sum_{i=1}^N x_i^2}, | \sqrt{\sum_{i=1}^N x_i^2}, | ||
\qquad x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | \qquad x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | ||
(norma euklidesowa),<br> | (norma euklidesowa),<br> | ||
<math> | <math> | ||
\|x\|_{1} | \|x\|_{1} | ||
\stackrel{df}{=} | \stackrel{df}{=} | ||
| Linia 84: | Linia 84: | ||
\qquad x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | \qquad x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | ||
(norma taksówkowa),<br> | (norma taksówkowa),<br> | ||
<math> | <math> | ||
\|x\|_{\infty} | \|x\|_{\infty} | ||
\stackrel{df}{=} | \stackrel{df}{=} | ||
| Linia 103: | Linia 103: | ||
Jeśli | Jeśli | ||
<math> | <math>(X,\|\cdot\|)</math> jest przestrzenią unormowaną, | ||
<math> | <math>d\colon X\times X\longrightarrow\mathbb{R}_+</math> | ||
jest funkcją zadaną przez | jest funkcją zadaną przez | ||
<math> | <math>d(x,y)\stackrel{df}{=}\|x-y\|</math>, | ||
to | to | ||
<math> | <math>(X,d)</math> jest przestrzenią metryczną.<br> | ||
Mówimy, że <math> | Mówimy, że <math>d</math> jest | ||
'''''metryką zadaną przez normę''''' <math> | '''''metryką zadaną przez normę''''' <math>\|\cdot\|</math>. | ||
}} | }} | ||
{{dowod|3.3.|| | {{dowod|3.3.|| | ||
Załóżmy, że <math> | Załóżmy, że <math>\|\cdot\|</math> jest normą w <math>X</math>. | ||
Pokażemy, że odwzorowanie | Pokażemy, że odwzorowanie | ||
<math> | <math>d\colon X\times X\longrightarrow\mathbb{R}_+</math> | ||
zadane przez <math> | zadane przez <math>d(x,y)\stackrel{df}{=}\|x-y\|</math> | ||
jest metryką w <math> | jest metryką w <math>X</math>.<br> | ||
'''(1)''' | '''(1)''' | ||
Zauważmy, że dla dowolnych <math> | Zauważmy, że dla dowolnych <math>x,y\in X</math>: | ||
<center><math> | <center><math>d(x,y) | ||
= | |||
\|x-y\| | \|x-y\| | ||
\ge | |||
0 | 0 | ||
</math></center> | </math></center> | ||
| Linia 132: | Linia 132: | ||
oraz | oraz | ||
<center><math> | <center><math>d(x,y)=0 | ||
\quad\Longleftrightarrow\quad | \quad\Longleftrightarrow\quad | ||
\|x-y\|=0 | \|x-y\|=0 | ||
\quad\Longleftrightarrow\quad | \quad\Longleftrightarrow\quad | ||
x=y | x=y</math></center> | ||
</math></center> | |||
'''(2)''' | '''(2)''' | ||
Dla dowolnych <math> | Dla dowolnych <math>x,y\in X</math> mamy | ||
<center><math> | <center><math>d(x,y) | ||
= | |||
\|x-y\| | \|x-y\| | ||
= | |||
|-1|\|x-y\| | |-1|\|x-y\| | ||
= | |||
\|(-1)(x-y)\| | \|(-1)(x-y)\| | ||
= | |||
\|-x+y\| | \|-x+y\| | ||
= | |||
\|y-x\| | \|y-x\| | ||
= | |||
d(y,x) | d(y,x)</math></center> | ||
</math></center> | |||
'''(3)''' | '''(3)''' | ||
Dla dowolnych <math> | Dla dowolnych <math>x,y,z\in X</math> mamy | ||
<center><math> | <center><math>d(x,y) | ||
= | |||
\|x-y\| | \|x-y\| | ||
= | |||
\|x-z+z-y\| | \|x-z+z-y\| | ||
\le | |||
\|x-z\|+\|z-y\| | \|x-z\|+\|z-y\| | ||
= | |||
d(x,z)+d(z,y) | d(x,z)+d(z,y)</math>,</center> | ||
</math></center> | |||
a więc zachodzi warunek trójkąta dla <math> | a więc zachodzi warunek trójkąta dla <math>d</math>. | ||
Pokazaliśmy zatem, że <math> | Pokazaliśmy zatem, że <math>d</math> jest metryką. | ||
}} | }} | ||
| Linia 188: | Linia 185: | ||
'''''zbieżnością silną''''' lub | '''''zbieżnością silną''''' lub | ||
'''''zbieżnością w normie''''', to znaczy | '''''zbieżnością w normie''''', to znaczy | ||
jeśli <math> | jeśli <math>\{x_n\}\subseteq X</math> jest ciągiem, to | ||
<center><math> | <center><math> | ||
x_n | x_n | ||
\ \stackrel{\|\cdot\|}{\longrightarrow} | \ \stackrel{\|\cdot\|}{\longrightarrow} | ||
x | x | ||
\ \ \ \stackrel{df}{\Longleftrightarrow} | \ \ \ \stackrel{df}{\Longleftrightarrow}\ \ | ||
\|x_n-x\| | \|x_n-x\| | ||
\ \longrightarrow | \ \longrightarrow | ||
0 | 0</math></center> | ||
</math></center> | |||
'''(4)''' | '''(4)''' | ||
| Linia 210: | Linia 206: | ||
{{definicja|3.5.|| | {{definicja|3.5.|| | ||
Dwie normy <math> | Dwie normy <math>\|\cdot\|_{a}</math> i <math>\|\cdot\|_{b}</math> w | ||
przestrzeni unormowanej <math> | przestrzeni unormowanej <math>X</math> nazywamy | ||
'''''równoważnymi''''', jeśli | '''''równoważnymi''''', jeśli | ||
<center><math> | <center><math>\exists m,M>0\ | ||
\forall x\in X: | \forall x\in X: | ||
m\|x\|_{a} | m\|x\|_{a} | ||
\le | |||
\|x\|_{b} | \|x\|_{b} | ||
\le | |||
M\|x\|_{a} | M\|x\|_{a}</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 234: | Linia 229: | ||
przestrzeni unormowanej.<br> | przestrzeni unormowanej.<br> | ||
'''(2)''' | '''(2)''' | ||
Normy: euklidesowa <math> | Normy: euklidesowa <math>\|\cdot\|_2</math>; maksimowa <math>\|\cdot\|_{\infty}</math> taksówkowa <math>\|\cdot\|_1</math> są równoważne | ||
(będzie to pokazane na ćwiczeniach; patrz [[Analiza matematyczna 2/Ćwiczenia 3: Norma. Iloczyn skalarny#cw_3_3|ćwiczenie 3.3.]]). | (będzie to pokazane na ćwiczeniach; patrz [[Analiza matematyczna 2/Ćwiczenia 3: Norma. Iloczyn skalarny#cw_3_3|ćwiczenie 3.3.]]). | ||
Okazuje się, że w przestrzeniach wektorowych skończenie wymiarowych wszystkie normy są równoważne. | Okazuje się, że w przestrzeniach wektorowych skończenie wymiarowych wszystkie normy są równoważne. | ||
| Linia 241: | Linia 236: | ||
{{Twierdzenie|3.7.|| | {{Twierdzenie|3.7.|| | ||
Twierdzenie to podajemy tu bez dowodu. Wszystkie normy w <math> | Twierdzenie to podajemy tu bez dowodu. Wszystkie normy w <math>\mathbb{R}^N</math> są równoważne. | ||
Kolejne twierdzenie mówi, że | Kolejne twierdzenie mówi, że | ||
odwzorowanie normy <math> | odwzorowanie normy <math>\|\cdot\|\colon X\longrightarrow\mathbb{R}_+</math> jest ciągłe | ||
(oczywiście w przestrzeni <math> | (oczywiście w przestrzeni <math>X</math> rozważamy metrykę zadaną przez normę, | ||
a w <math> | a w <math>\mathbb{R}</math> metrykę euklidesową). | ||
}} | }} | ||
<span id="tw_3_8">{{twierdzenie|3.8.|| | <span id="tw_3_8">{{twierdzenie|3.8.|| | ||
Wszystkie normy w <math> | Wszystkie normy w <math>\mathbb{R}^{N}</math> są równoważne. | ||
}}</span> | }}</span> | ||
| Linia 256: | Linia 251: | ||
Norma jest funkcją ciągłą, to znaczy | Norma jest funkcją ciągłą, to znaczy | ||
<center><math> | <center><math>\lim\limits_{n\rightarrow +\infty} x_n = x | ||
\ \ \ \Longrightarrow | \ \ \ \Longrightarrow \ | ||
\lim\limits_{n\rightarrow +\infty}\|x_n\|=\|x\| | \lim\limits_{n\rightarrow +\infty}\|x_n\|=\|x\|</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 269: | Linia 263: | ||
Jeśli | Jeśli | ||
<math> | <math>X</math> jest przestrzenią unormowaną, | ||
to | to | ||
<center><math> | <center><math>\forall x,y\in X: | ||
\big|\|x\|-\|y\|\big| | \big|\|x\|-\|y\|\big| | ||
\le | |||
\|x-y\| | \|x-y\|</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 283: | Linia 276: | ||
Korzystając z subaddytywności normy, dla dowolnych | Korzystając z subaddytywności normy, dla dowolnych | ||
<math> | <math>x,y\in X</math> mamy | ||
<center><math> | <center><math>\|x\| | ||
= | |||
\|x+(-y)+y\| | \|x+(-y)+y\| | ||
\le | |||
\|x-y\|+\|y\| | \|x-y\|+\|y\|</math>,</center> | ||
</math></center> | |||
czyli | czyli | ||
<center><math> | <center><math>\|x\|-\|y\| | ||
\le | |||
\|x-y\| | \|x-y\|</math></center> | ||
</math></center> | |||
Analogicznie pokazujemy, że | Analogicznie pokazujemy, że | ||
<center><math> | <center><math>\|y\|-\|x\| | ||
\le | |||
\|x-y\| | \|x-y\|</math></center> | ||
</math></center> | |||
Obie powyższe nierówności implikują nierówność w tezie lematu. | Obie powyższe nierówności implikują nierówność w tezie lematu. | ||
| Linia 310: | Linia 300: | ||
{{dowod|3.8.|| | {{dowod|3.8.|| | ||
Warunek <math> | Warunek <math>\lim\limits_{n\rightarrow +\infty} x_n = x</math> oznacza, że | ||
<center><math> | <center><math>\lim\limits_{n\rightarrow +\infty} \|x_n-x\| | ||
= | |||
0 | 0</math></center> | ||
</math></center> | |||
Ustalmy dowolne <math> | Ustalmy dowolne <math>\varepsilon>0</math>. | ||
Z powyższej równości wynika, że | Z powyższej równości wynika, że | ||
<center><math> | <center><math>\exists N\forall n\ge N: | ||
\|x_n-x\| | \|x_n-x\| | ||
\le | |||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Zatem dla | Zatem dla | ||
<math> | <math>n\ge N</math> mamy | ||
<center><math> | <center><math>\big|\|x_n\|-\|x\|\big| | ||
\le | |||
\|x_n-x\| | \|x_n-x\| | ||
\le | |||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Zatem pokazaliśmy, że <math> | Zatem pokazaliśmy, że <math>\|x_n\|\stackrel{\mathbb{R}}{\longrightarrow}\|x\|</math>. | ||
}} | }} | ||
| Linia 343: | Linia 330: | ||
'''(1)''' | '''(1)''' | ||
Implikacja odwrotna do implikacji w [[#tw_3_7|twierdzenieu 3.7.]] nie jest prawdziwa.<br> | Implikacja odwrotna do implikacji w [[#tw_3_7|twierdzenieu 3.7.]] nie jest prawdziwa.<br> | ||
Aby to zobaczyć, rozważmy ciąg <math> | Aby to zobaczyć, rozważmy ciąg <math>\{x_n\}\subseteq \mathbb{R}</math> | ||
zadany przez | zadany przez | ||
<math> | <math>x_n=(-1)^n</math>. | ||
Wówczas | Wówczas | ||
<center><math> | <center><math>\|x_n\|_2 | ||
= | |||
1 | 1 | ||
\ \longrightarrow | \ \longrightarrow | ||
1 | 1</math>,</center> | ||
</math></center> | |||
ale sam ciąg <math> | ale sam ciąg <math>\{x_n\}</math> nie jest silnie zbieżny | ||
(dlaczego?)<br> | (dlaczego?)<br> | ||
'''(2)''' | '''(2)''' | ||
Jeżeli granicą ciągu <math> | Jeżeli granicą ciągu <math>\{x_n\}</math> jest <math>\Theta</math> | ||
(wektor "zerowy" przestrzeni wektorowej), | (wektor "zerowy" przestrzeni wektorowej), | ||
to implikację w [[#tw_3_7|twierdzenieu 3.7.]] można odwrócić, to znaczy zachodzi równoważność: | to implikację w [[#tw_3_7|twierdzenieu 3.7.]] można odwrócić, to znaczy zachodzi równoważność: | ||
<center><math> | <center><math>\lim\limits_{n\rightarrow +\infty} x_n = \Theta | ||
\ \ \ \Longleftrightarrow | \ \ \ \Longleftrightarrow\ \ | ||
\lim\limits_{n\rightarrow +\infty}\|x_n\|=0 | \lim\limits_{n\rightarrow +\infty}\|x_n\|=0 | ||
</math></center> | </math></center> | ||
| Linia 374: | Linia 360: | ||
{{definicja|3.11.|| | {{definicja|3.11.|| | ||
Niech <math> | Niech <math>X</math> będzie przestrzenią unormowaną oraz | ||
<math> | <math>A\subseteq X</math>.<br> | ||
'''(1)''' | '''(1)''' | ||
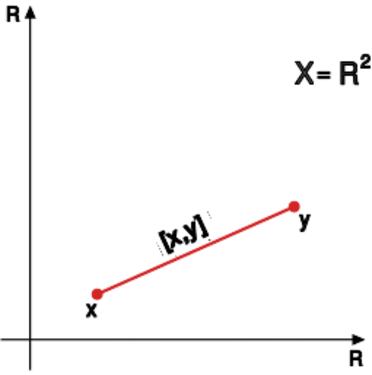
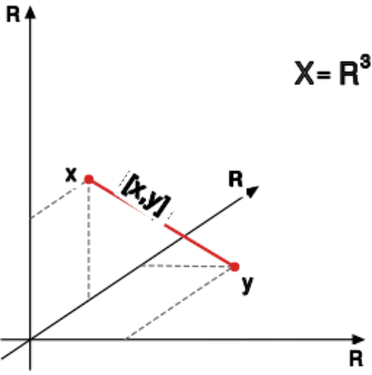
Jeśli <math> | Jeśli <math>x,y\in X</math>, | ||
to '''''odcinkiem''''' w <math> | to '''''odcinkiem''''' w <math>X</math> łączącym punkty <math>x</math> i <math>y</math> | ||
nazywamy zbiór | nazywamy zbiór | ||
<center><math> | <center><math>[x,y] | ||
\ \stackrel{df}{=}\ | \ \stackrel{df}{=}\ | ||
\bigg\{z\in X: | \bigg\{z\in X: | ||
z=\lambda x+(1-\lambda)y: | z=\lambda x+(1-\lambda)y:\ | ||
\lambda\in[0,1]\bigg\} | \lambda\in[0,1]\bigg\}</math></center> | ||
</math></center> | |||
'''(2)''' | '''(2)''' | ||
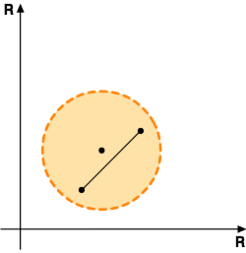
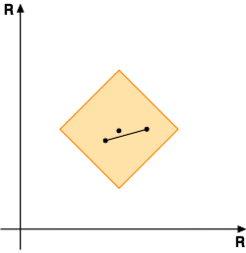
Mówimy, że zbiór <math> | Mówimy, że zbiór <math>A</math> jest '''''wypukły''''', jeśli | ||
<center><math> | <center><math>\forall x,y\in A:\ | ||
[x,y]\subseteq A | [x,y]\subseteq A</math></center>}} | ||
</math></center>}} | |||
{| border="0" align="center" cellspacing="10" | {| border="0" align="center" cellspacing="10" | ||
| | |[[File:AM2.M03.W.R01.svg|375x375px|thumb|center|Odcinek w <math>\mathbb{R}^2</math>]] | ||
|[[File:AM2.M03.W.R02.svg|375x375px|thumb|center|Odcinek w <math>\mathbb{R}^3</math>]] | |||
| | |||
|} | |} | ||
{| border="0" align="center" cellspacing="10" | {| border="0" align="center" cellspacing="10" | ||
| | |[[File:AM2.M03.W.R03.svg|253x253px|thumb|center|Zbiór wypukły]] | ||
|[[File:AM2.M03.W.R04.svg|253x253px|thumb|center|Zbiór, który nie jest wypukły]] | |||
| | |||
|} | |} | ||
| Linia 426: | Linia 398: | ||
}} | }} | ||
{| border="0" align="center" cellspacing="10" | {| border="0" align="center" cellspacing="10" | ||
| | |[[File:AM2.M03.W.R05.svg|253x253px|thumb|center|Wypukłość kuli w metryce eukildesowej]] | ||
|[[File:AM2.M03.W.R06.svg|253x253px|thumb|center|Wypukłość kuli w metryce taksówkowej]] | |||
|[[File:AM2.M03.W.R07.svg|253x253px|thumb|center|Wypukłość kuli w metryce maksimowej]] | |||
| | |||
|} | |} | ||
{{dowod|3.12.|| | {{dowod|3.12.|| | ||
Niech <math> | Niech <math>a\in X</math> oraz <math>r>0</math>. | ||
Pokażemy, że kula <math> | Pokażemy, że kula <math>K(a,r)</math> jest zbiorem wypukłym. | ||
W tym celu wybierzmy dowolne | W tym celu wybierzmy dowolne | ||
<math> | <math>x_1,x_2\in K(a,r)</math>. | ||
Z definicji kuli wynika, że | Z definicji kuli wynika, że | ||
<center><math> | <center><math>\|x_1-a\| <r,\quad | ||
\|x_2-a\|<r | \|x_2-a\|<r</math></center> | ||
</math></center> | |||
Niech <math> | Niech <math>x\in[x_1,x_2]</math>. | ||
Należy pokazać, że <math> | Należy pokazać, że <math>x\in K(a,r)</math>. | ||
Z definicji odcinka w <math> | Z definicji odcinka w <math>X</math> wiemy, że | ||
<center><math> | <center><math>\exists \lambda\in[0,1]: | ||
x=\lambda x_1+(1-\lambda)x_2 | x=\lambda x_1+(1-\lambda)x_2</math></center> | ||
</math></center> | |||
Zatem | Zatem | ||
<center><math> | <center><math>\|x-a\| | ||
= | |||
\|\lambda x_1+(1-\lambda)x_2-a\| | \|\lambda x_1+(1-\lambda)x_2-a\| | ||
= | |||
\|\lambda(x_1-a)+(1-\lambda)(x_2-a)\| | \|\lambda(x_1-a)+(1-\lambda)(x_2-a)\| | ||
\le | |||
\lambda\|x_1-a\|+(1-\lambda)\|x_2-a\| | \lambda\|x_1-a\|+(1-\lambda)\|x_2-a\| | ||
< | |||
\lambda r+(1-\lambda)r | \lambda r+(1-\lambda)r | ||
= | |||
r | r</math></center> | ||
</math></center> | |||
Zatem pokazaliśmy, że <math> | Zatem pokazaliśmy, że <math>x\in K(a,r)</math>. Dowód, że <math>\overline{K}(a,r)</math> jest zbiorem wypukłym, jest analogiczny. | ||
}} | }} | ||
| Linia 479: | Linia 443: | ||
<span id="wn_3_13">{{wniosek|3.13.|| | <span id="wn_3_13">{{wniosek|3.13.|| | ||
Metryka kolejowa i metryka rzeka w <math> | Metryka kolejowa i metryka rzeka w <math>\mathbb{R}^2</math> nie są | ||
zadane przez żadną normę, ponieważ kule w tych metrykach | zadane przez żadną normę, ponieważ kule w tych metrykach | ||
nie są zbiorami wypukłymi | nie są zbiorami wypukłymi | ||
| Linia 487: | Linia 451: | ||
{| border="0" align="center" cellspacing="10" | {| border="0" align="center" cellspacing="10" | ||
| | |[[File:AM2.M03.W.R08.svg|253x253px|thumb|center|Kula w metryce rzece nie jest wypukła]] | ||
|[[File:AM2.M03.W.R09.svg|253x253px|thumb|center|Kula w metryce kolejowej nie jest wypukła]] | |||
| | |||
|} | |} | ||
| Linia 514: | Linia 472: | ||
'''(1)''' | '''(1)''' | ||
<math> | <math>\big(\mathbb{R}^N,\|\cdot\|_{2}\big)</math> jest przestrzenią Banacha | ||
(patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#wn_2_21|wniosek 2.21.]]).<br> | (patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#wn_2_21|wniosek 2.21.]]).<br> | ||
'''(2)''' | '''(2)''' | ||
Przestrzeń | Przestrzeń | ||
<math> | <math>C\big([a,b];\mathbb{R}\big)</math> z normą | ||
<math> | <math>\|f\|_{\infty}=\sup\limits_{x\in[a,b]}\big|f(x)\big|</math> | ||
jest przestrzenią Banacha | jest przestrzenią Banacha | ||
(patrz [[Analiza matematyczna 2/Ćwiczenia 3: Norma. Iloczyn skalarny#cw_3_5|ćwiczenie 3.5.]]). | (patrz [[Analiza matematyczna 2/Ćwiczenia 3: Norma. Iloczyn skalarny#cw_3_5|ćwiczenie 3.5.]]). | ||
| Linia 534: | Linia 492: | ||
{{definicja|3.15.|def_3_15| | {{definicja|3.15.|def_3_15| | ||
Niech <math> | Niech <math>X</math> będzie rzeczywistą przestrzenią wektorową. | ||
Odwzorowanie | Odwzorowanie | ||
<math> | <math>(\cdot|\cdot)\colon X\times X\longrightarrow \mathbb{R}</math> | ||
nazywamy '''''iloczynem skalarnym''''' w <math> | nazywamy '''''iloczynem skalarnym''''' w <math>X</math>, jeśli:<br> | ||
'''(1)''' | '''(1)''' | ||
<math> | <math>\forall x\in X: | ||
\big[(x|x)\ge 0\big] | \big[(x|x)\ge 0\big] | ||
\ | \ </math> i <math> | ||
\big[ | \big[ | ||
(x|x)=0 | (x|x)=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
x=\Theta | x=\Theta | ||
\big] | \big]</math>,<br> | ||
'''(2)''' | '''(2)''' | ||
<math> | <math>\forall x,y\in X,\ \lambda\in\mathbb{R}: | ||
(\lambda x|y)=\lambda(x|y) | (\lambda x|y)=\lambda(x|y)</math>,<br> | ||
'''(3)''' | '''(3)''' | ||
<math> | <math>\forall x,y,z\in X: | ||
(x+y|z)=(x|z)+(y|z) | (x+y|z)=(x|z)+(y|z)</math>,<br> | ||
'''(4)''' | '''(4)''' | ||
<math> | <math>\forall x,y\in X: | ||
(x|y)=(y|x)</math> | (x|y)=(y|x)</math> | ||
(symetria).<br> | (symetria).<br> | ||
Parę <math> | Parę <math>(X,(\cdot|\cdot))</math> nazywamy | ||
'''''przestrzenią unitarną'''''. | '''''przestrzenią unitarną'''''. | ||
}} | }} | ||
| Linia 575: | Linia 533: | ||
Odwzorowanie zdefiniowane przez | Odwzorowanie zdefiniowane przez | ||
<center><math> | <center><math>(x|y) | ||
\ \stackrel{df}{=}\ | \ \stackrel{df}{=}\ | ||
\sum_{i=1}^N x_iy_i | |||
\quad </math> dla <math> | \quad</math> dla <math>\ x=(x_1,\ldots,x_N),\ y=(y_1,\ldots,y_N)\in\mathbb{R}^N | ||
</math></center> | </math></center> | ||
jest iloczynem skalarnym w <math> | jest iloczynem skalarnym w <math>\mathbb{R}^N</math>. | ||
Nazywamy go | Nazywamy go | ||
'''''standardowym iloczynem skalarnym''''' w <math> | '''''standardowym iloczynem skalarnym''''' w <math>\mathbb{R}^N</math>. | ||
Iloczyn ten znamy ze szkoły dla przestrzeni | Iloczyn ten znamy ze szkoły dla przestrzeni | ||
<math> | <math>\mathbb{R}^2</math> i <math>\mathbb{R}^3</math>. | ||
Sprawdzimy kolejno punkty definicji iloczynu skalarnego.<br> | Sprawdzimy kolejno punkty definicji iloczynu skalarnego.<br> | ||
'''(1)''' | '''(1)''' | ||
Dla dowolnego <math> | Dla dowolnego <math>x\in\mathbb{R}^N</math> mamy | ||
<center><math> | <center><math>(x|x) | ||
= | |||
\sum_{n=1}^N x_i^2 | \sum_{n=1}^N x_i^2 | ||
\ge | |||
0 | 0 | ||
</math></center> | </math></center> | ||
| Linia 600: | Linia 558: | ||
oraz | oraz | ||
<center><math> | <center><math>(x|x)=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
\sum_{n=1}^N x_i^2=0 | \sum_{n=1}^N x_i^2=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
x_1=\ldots=x_N | x_1=\ldots=x_N | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
x=\Theta | x=\Theta</math></center> | ||
</math></center> | |||
'''(2)''' | '''(2)''' | ||
Dla dowolnych <math> | Dla dowolnych <math>x,y\in\mathbb{R}^N</math> | ||
oraz <math> | oraz <math>\lambda\in\mathbb{R}</math> mamy | ||
<center><math> | <center><math>(\lambda x,y) | ||
= | |||
\sum_{n=1}^N \lambda x_iy_i | \sum_{n=1}^N \lambda x_iy_i | ||
= | |||
\lambda \sum_{n=1}^N x_iy_i | \lambda \sum_{n=1}^N x_iy_i | ||
= | |||
\lambda (x|y) | \lambda (x|y) | ||
</math></center> | </math></center> | ||
'''(3)''' | '''(3)''' | ||
Dla dowolnych <math> | Dla dowolnych <math>x,y,z\in\mathbb{R}^N</math> mamy | ||
<center><math> | <center><math>(x+y|z) | ||
= | |||
\sum_{n=1}^N (x_i+y_i)z_i | \sum_{n=1}^N (x_i+y_i)z_i | ||
= | |||
\sum_{n=1}^N(x_iz_i+y_iz_i) | \sum_{n=1}^N(x_iz_i+y_iz_i) | ||
= | |||
\sum_{n=1}^N x_iz_i | \sum_{n=1}^N x_iz_i | ||
+\sum_{n=1}^Ny_iz_i | +\sum_{n=1}^Ny_iz_i | ||
= | |||
(x|z)+(y|z) | (x|z)+(y|z)</math></center> | ||
</math></center> | |||
'''(4)''' | '''(4)''' | ||
Dla dowolnych <math> | Dla dowolnych <math>x,y\in\mathbb{R}^N</math> mamy | ||
<center><math> | <center><math>(x|y) | ||
= | |||
\sum_{n=1}^N x_iy_i | \sum_{n=1}^N x_iy_i | ||
= | |||
\sum_{n=1}^N y_ix_i | \sum_{n=1}^N y_ix_i | ||
= | |||
(y|x) | (y|x)</math></center> | ||
</math></center> | |||
Zatem pokazaliśmy, że odwzorowanie | Zatem pokazaliśmy, że odwzorowanie | ||
<math> | <math>(x|y)=\sum_{i=1}^N x_iy_i</math> | ||
jest iloczynem skalarnym w <math> | jest iloczynem skalarnym w <math>\mathbb{R}^N</math>. | ||
}}</span> | }}</span> | ||
| Linia 660: | Linia 615: | ||
Jeśli | Jeśli | ||
<math> | <math>(X,(\cdot|\cdot))</math> jest przestrzenią unitarną oraz | ||
<math> | <math>\forall x\in X: \|x\|_{}\ \stackrel{df}{=}\ \sqrt{(x|x)}</math>, | ||
to | to | ||
<math> | <math>\|\cdot\|_{}</math> jest normą w <math>X</math>.<br> | ||
Mówimy, że <math> | Mówimy, że <math>\|\cdot\|_{}</math> jest | ||
'''''normą zadaną przez iloczyn skalarny''''' | '''''normą zadaną przez iloczyn skalarny''''' | ||
<math> | <math>(\cdot|\cdot)</math>. | ||
}} | }} | ||
| Linia 673: | Linia 628: | ||
{{lemat|3.19. [nierówność Schwarza]|| | {{lemat|3.19. [nierówność Schwarza]|| | ||
Jeśli <math> | Jeśli <math>(X,(\cdot|\cdot))</math> jest przestrzenią unitarną, to | ||
<center><math> | <center><math>\forall x,y\in X: | ||
\left|(x|y)\right|\le\|x\|\|y\| | \left|(x|y)\right|\le\|x\|\|y\|</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 683: | Linia 637: | ||
{{dowod|3.20.|| | {{dowod|3.20.|| | ||
Ustalmy dowolne <math> | Ustalmy dowolne <math>x,y\in X</math>. | ||
Jeśli <math> | Jeśli <math>y=\Theta</math> to powyższa nierówność jest oczywistą równością. | ||
Załóżmy, że <math> | Załóżmy, że <math>y\ne \Theta</math>. | ||
Niech | Niech | ||
<math> | <math>\lambda=\frac{(x|y)}{(y|y)}</math> | ||
Korzystając z dwuliniowości iloczynu skalarnego, mamy: | Korzystając z dwuliniowości iloczynu skalarnego, mamy: | ||
<center><math> | <center><math>0 | ||
\le | |||
(x-\lambda y|x-\lambda y) | (x-\lambda y|x-\lambda y) | ||
= | |||
(x|x)-2\lambda(x|y)+\lambda^2(y|y) | (x|x)-2\lambda(x|y)+\lambda^2(y|y) | ||
= | |||
(x|x)-2\frac{(x|y)^2}{(y|y)} | (x|x)-2\frac{(x|y)^2}{(y|y)} | ||
+\frac{(x|y)^2}{(y|y)} | +\frac{(x|y)^2}{(y|y)} | ||
</math></center> | </math></center> | ||
<center><math> | <center><math>= | ||
(x|x) | (x|x) | ||
-\frac{(x|y)^2}{(y|y)} | -\frac{(x|y)^2}{(y|y)} | ||
= | |||
\|x\|-\frac{(x|y)^2}{\|y\|} | \|x\|-\frac{(x|y)^2}{\|y\|}</math></center> | ||
</math></center> | |||
Zatem mamy | Zatem mamy | ||
<center><math> | <center><math>\frac{(x|y)^2}{\|y\|^2} | ||
\le | |||
\|x\|^2 | \|x\|^2</math>,</center> | ||
</math></center> | |||
skąd | skąd | ||
<center><math> | <center><math>(x|y)^2 | ||
\le | |||
\|x\|^2\cdot \|y\|^2 | \|x\|^2\cdot \|y\|^2</math>,</center> | ||
</math></center> | |||
a zatem | a zatem | ||
<center><math> | <center><math>|(x|y)| | ||
\le | |||
\|x\|\cdot\|y\| | \|x\|\cdot\|y\|</math>,</center> | ||
</math></center> | |||
co należało dowieść. | co należało dowieść. | ||
| Linia 735: | Linia 685: | ||
Zauważmy, że nierówność Cauchy'ego | Zauważmy, że nierówność Cauchy'ego | ||
(patrz [[Analiza matematyczna 1/Wykład 3: Odległość i ciągi#lemat_3_8|lemat 3.8.]]) jest szczególnym przypadkiem nierówności | (patrz [[Analiza matematyczna 1/Wykład 3: Odległość i ciągi#lemat_3_8|lemat 3.8.]]) jest szczególnym przypadkiem nierówności | ||
Schwarza, gdy w przestrzeni <math> | Schwarza, gdy w przestrzeni <math>\mathbb{R}^N</math> mamy standardowy iloczyn skalarny. | ||
}} | }} | ||
| Linia 741: | Linia 691: | ||
'''(1)''' | '''(1)''' | ||
<center><math> | <center><math>\|x\|=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
(x|x)=0 | (x|x)=0 | ||
\ \Longleftrightarrow x=\Theta | \ \Longleftrightarrow x=\Theta</math>,</center> | ||
</math></center> | |||
a więc pierwszy warunek w definicji normy jest spełniony.<br> | a więc pierwszy warunek w definicji normy jest spełniony.<br> | ||
'''(2)''' | '''(2)''' | ||
<center><math> | <center><math>\|\lambda x\| | ||
= | |||
\sqrt{(\lambda x|\lambda x)} | \sqrt{(\lambda x|\lambda x)} | ||
= | |||
\sqrt{\lambda^2}\sqrt{(x|x)} | \sqrt{\lambda^2}\sqrt{(x|x)} | ||
= | |||
|\lambda|\|x\| | |\lambda|\|x\|</math>,</center> | ||
</math></center> | |||
zatem drugi warunek (jednorodność) w definicji normy jest spełniony.<br> | zatem drugi warunek (jednorodność) w definicji normy jest spełniony.<br> | ||
| Linia 763: | Linia 711: | ||
Korzystając z nierówności Schwarza, mamy | Korzystając z nierówności Schwarza, mamy | ||
<center><math> | <center><math>\|x+y\|^2 | ||
= | |||
(x+y|x+y) | (x+y|x+y) | ||
= | |||
(x|x)+2(x|y)+(y|y) | (x|x)+2(x|y)+(y|y) | ||
\le | |||
\|x\|^2+2\|x\|\cdot\|y\| | \|x\|^2+2\|x\|\cdot\|y\| | ||
+\|y^2\| | +\|y^2\| | ||
= | |||
(\|x\|+\|y\|)^2 | (\|x\|+\|y\|)^2</math>,</center> | ||
</math></center> | |||
a więc | a więc | ||
<center><math> | <center><math>\|x+y\| | ||
\le | |||
\|x\|+\|y\| | \|x\|+\|y\|</math></center> | ||
</math></center> | |||
zatem trzeci warunek (subaddytywność) w definicji normy jest spełniony. | zatem trzeci warunek (subaddytywność) w definicji normy jest spełniony. | ||
| Linia 787: | Linia 733: | ||
{{przyklad|3.22.|| | {{przyklad|3.22.|| | ||
Iloczyn skalarny w <math> | Iloczyn skalarny w <math>\mathbb{R}^N</math> dany wzorem | ||
(patrz [[#prz_3_17|przykład 3.17.]]) | (patrz [[#prz_3_17|przykład 3.17.]]) | ||
<center><math> | <center><math>(x|y) | ||
\ \stackrel{df}{=}\ | \ \stackrel{df}{=}\ | ||
\sum_{i=1}^N x_iy_i | |||
\quad </math> dla <math> | \quad</math> dla <math>\ x=(x_1,\ldots,x_N),\ y=(y_1,\ldots,y_N)\in\mathbb{R}^N | ||
</math></center> | </math></center> | ||
zadaje normę euklidesową, bo | zadaje normę euklidesową, bo | ||
<center><math> | <center><math>\sqrt{(x|x)} | ||
= | |||
\sqrt{ | \sqrt{\sum_{i=1}^N x_i^2} | ||
= | |||
\|x\|_{2} | \|x\|_{2}</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 822: | Linia 767: | ||
<center> | <center> | ||
<math> | <math> | ||
\bigg[ | \bigg[ | ||
x_n\stackrel{X}{\longrightarrow} x, | x_n\stackrel{X}{\longrightarrow} x, | ||
y_n\stackrel{X}{\longrightarrow} y | y_n\stackrel{X}{\longrightarrow} y | ||
\bigg] | \bigg] | ||
\ \ \Longrightarrow | \ \ \Longrightarrow | ||
\bigg[ | \bigg[ | ||
(x_n|y_n) | (x_n|y_n) | ||
\ \stackrel{\mathbb{R}}{\longrightarrow} | \ \stackrel{\mathbb{R}}{\longrightarrow} | ||
(x|y) | (x|y) | ||
\bigg] | \bigg] | ||
| Linia 836: | Linia 781: | ||
</center> | </center> | ||
(oczywiście zbieżność <math> | (oczywiście zbieżność <math>x_n\stackrel{X}{\longrightarrow} x</math> oznacza zbieżność | ||
w normie zadanej | w normie zadanej | ||
przez iloczyn skalarny <math> | przez iloczyn skalarny <math>(\cdot|\cdot)</math>). | ||
}} | }} | ||
{{dowod|3.24. [dowód nadobowiązkowy]|| | {{dowod|3.24. [dowód nadobowiązkowy]|| | ||
Niech <math> | Niech <math>\{(x_n,y_n)\}</math> będzie ciągiem takim, że | ||
<math> | <math>x_n\stackrel{X}{\longrightarrow} x</math> i | ||
<math> | <math>y_n\stackrel{X}{\longrightarrow} y</math>. | ||
Oznacza to, że | Oznacza to, że | ||
<center> | <center> | ||
<math> | <math>\|x_n-x\| | ||
\ \longrightarrow | \ \longrightarrow | ||
0,\quad | 0,\quad | ||
\|y_n-y\| | \|y_n-y\| | ||
\ \longrightarrow | \ \longrightarrow | ||
0 | 0 | ||
</math> | </math> | ||
| Linia 860: | Linia 805: | ||
<center> | <center> | ||
<math> | <math>\|x_n\|\longrightarrow \|x\|</math> | ||
</math> | |||
</center> | </center> | ||
Korzystając z nierówności Schwarza, mamy | Korzystając z nierówności Schwarza, mamy | ||
<center><math> | <center><math>\big|(x_n|y_n)-(x|y)\big| | ||
= | |||
\big|(x_n|y_n)-(x_n|y)+(x_n|y)-(x|y)\big| | \big|(x_n|y_n)-(x_n|y)+(x_n|y)-(x|y)\big| | ||
\le | |||
\big|(x_n|y_n-y)+(x_n-x|y)\big| | \big|(x_n|y_n-y)+(x_n-x|y)\big| | ||
</math></center> | </math></center> | ||
<center><math> | <center><math>\le | ||
\|x_n\|\cdot\|y_n-y\| | \|x_n\|\cdot\|y_n-y\| | ||
+\|x_n-x\|\cdot\|y\| | +\|x_n-x\|\cdot\|y\|</math></center> | ||
</math></center> | |||
Z wyżej wskazanych zbieżności w <math> | Z wyżej wskazanych zbieżności w <math>\mathbb{R}</math> wynika, że | ||
prawa strona nierówności, | prawa strona nierówności, | ||
a zatem także lewa, zmierza do zera, gdy <math> | a zatem także lewa, zmierza do zera, gdy <math>n\rightarrow+\infty</math>. | ||
Oznacza to, że <math> | Oznacza to, że <math>(x_n|y_n)\stackrel{\mathbb{R}}{\longrightarrow}(x|y)</math>, | ||
co należało dowieść. | co należało dowieść. | ||
}} | }} | ||
| Linia 888: | Linia 831: | ||
wektorów. | wektorów. | ||
{| border="0" align="center" cellspacing="10" | {| border="0" align="center" cellspacing="10" | ||
| | |[[File:AM2.M03.W.R10.svg|375x375px|thumb|center|Wektory prostopadłe w <math>\mathbb{R}^2</math>]] | ||
|[[File:AM2.M03.W.R11.svg|375x375px|thumb|center|Wektory prostopadłe w <math>\mathbb{R}^3</math>]] | |||
< | |||
| | |||
< | |||
|} | |} | ||
[[File:AM2.M03.W.R12.mp4|253x253px|thumb|right|Wektor prostopadły do podprzestrzeni]] | |||
{{definicja|3.25.|def_3_25| | {{definicja|3.25.|def_3_25| | ||
Niech <math> | Niech <math>\big(X,(\cdot|\cdot)\big)</math> będzie przestrzenią | ||
unitarną.<br> | unitarną.<br> | ||
'''(1)''' | '''(1)''' | ||
Jeśli <math> | Jeśli <math>(x|y)=0</math>, to mówimy, że wektory | ||
<math> | <math>x</math> i <math>y</math> są '''''ortogonalne''''' (lub '''''prostopadłe''''') | ||
i piszemy <math> | i piszemy <math>x\perp y</math>.<br> | ||
}} | }} | ||
'''(2)''' | '''(2)''' | ||
Niech <math> | Niech <math>Y</math> będzie podprzestrzenią wektorową <math>X</math>. | ||
Mówimy, że wektor <math> | Mówimy, że wektor <math>x</math> jest '''''ortogonalny''''' | ||
('''''prostopadły''''', '''''normalny''''') do | ('''''prostopadły''''', '''''normalny''''') do | ||
podprzestrzeni <math> | podprzestrzeni <math>Y</math>, | ||
jeśli | jeśli | ||
<br><center> | <br><center> | ||
<math> | <math>\forall y\in Y: | ||
x\perp y | x\perp y</math> | ||
</math> | |||
<br></center> | <br></center> | ||
Piszemy <math> | Piszemy <math>x\perp Y</math>.<br> | ||
'''(3)''' | '''(3)''' | ||
Mówimy, że wektory <math> | Mówimy, że wektory <math>a_1,\ldots,a_k\in X</math> tworzą układ | ||
'''''ortogonalny''''', | '''''ortogonalny''''', | ||
jeśli | jeśli | ||
<br><center> | <br><center> | ||
<math> | <math>(a_i|a_j)=0 | ||
\qquad\forall\ i\ne j | \qquad\forall\ i\ne j</math> | ||
</math> | |||
<br></center> | <br></center> | ||
'''(4)''' | '''(4)''' | ||
Mówimy, że wektory <math> | Mówimy, że wektory <math>a_1,\ldots,a_k\in X</math> tworzą układ | ||
'''''ortonormalny''''', | '''''ortonormalny''''', | ||
jeśli | jeśli | ||
<br><center> | <br><center> | ||
<math> | <math> | ||
\forall i,j: | \forall i,j:\ | ||
(a_i|a_j)=\delta_{ij} | (a_i|a_j)=\delta_{ij} | ||
\ \stackrel{df}{=}\ | \ \stackrel{df}{=}\ | ||
| Linia 953: | Linia 885: | ||
0 & \quad i\ne j | 0 & \quad i\ne j | ||
\end{array} | \end{array} | ||
\right. | \right.</math> | ||
</math> | |||
<br></center> | <br></center> | ||
(to znaczy wektory <math> | (to znaczy wektory <math>a_1,\ldots,a_k</math> | ||
są parami ortogonalne oraz mają | są parami ortogonalne oraz mają | ||
normę <math> | normę <math>1</math>). | ||
Poniższe twierdzenie podamy tu bez dowodu. | Poniższe twierdzenie podamy tu bez dowodu. | ||
[[File:AM2.M03.W.R13.svg|375x375px|thumb|right|Suma i różnica wektorów w <math>\mathbb{R}^2</math> (ilustracja do warunku równoległoboku)]] | |||
[[File:AM2.M03.W.R14.svg|375x375px|thumb|right|Suma wektorów prostopadłych (ilustacja twierdzenia Pitagorasa)]] | |||
{{twierdzenie|3.26.|| | {{twierdzenie|3.26.|| | ||
| Linia 970: | Linia 904: | ||
}} | }} | ||
{{przyklad|3.27.|| | {{przyklad|3.27.|| | ||
Baza kanoniczna w <math> | Baza kanoniczna w <math>\mathbb{R}^N</math> jest bazą ortonormalną. | ||
}} | }} | ||
{{twierdzenie|3.28. [warunek równoległoboku]|| | {{twierdzenie|3.28. [warunek równoległoboku]|| | ||
Jeśli | Jeśli | ||
<math> | <math>\big(X,(\cdot|\cdot)\big)</math> jest przestrzenią unitarną oraz | ||
<math> | <math>\|\cdot\|</math> jest normą zadaną przez iloczyn skalarny, | ||
to | to | ||
<br><center> | <br><center> | ||
<math> | <math>\forall x,y\in X: | ||
\|x+y\|^{2} | \|x+y\|^{2} | ||
+\|x-y\|^{2} | +\|x-y\|^{2} | ||
= | |||
2\big(\|x\|^{2}+\|y\|^{2}\big) | 2\big(\|x\|^{2}+\|y\|^{2}\big)</math> | ||
</math> | |||
<br></center> | <br></center> | ||
| Linia 998: | Linia 927: | ||
{{dowod|3.28.|| | {{dowod|3.28.|| | ||
Dla dowolnych ustalonych <math> | Dla dowolnych ustalonych <math>x,y\in X</math> liczymy | ||
<br><center> | <br><center> | ||
<math> | <math>\|x+y\|^2 | ||
= | |||
\|x\|^2+2(x|y)+\|y\|^2 | \|x\|^2+2(x|y)+\|y\|^2</math>, | ||
</math> | |||
<br></center> | <br></center> | ||
| Linia 1010: | Linia 938: | ||
<br><center> | <br><center> | ||
<math> | <math>\|x-y\|^2 | ||
= | |||
\|x\|^2-2(x|y)+\|y\|^2 | \|x\|^2-2(x|y)+\|y\|^2</math> | ||
</math> | |||
<br></center> | <br></center> | ||
Dodając stronami powyższe równości, dostajemy tezę twierdzenia. | Dodając stronami powyższe równości, dostajemy tezę twierdzenia. | ||
}} | }} | ||
[[grafika:Pitagoras.jpg|thumb|left||Pitagoras (VI w. p.n.e.)<br>[[Biografia Pitagoras|Zobacz biografię]]]] | [[grafika:Pitagoras.jpg|thumb|left||Pitagoras (VI w. p.n.e.)<br>[[Biografia Pitagoras|Zobacz biografię]]]] | ||
{{twierdzenie|3.29. [Twierdzenie Pitagorasa]|| | {{twierdzenie|3.29. [Twierdzenie Pitagorasa]|| | ||
Jeśli | Jeśli | ||
<math> | <math>\big(X,(\cdot|\cdot)\big)</math> | ||
jest przestrzenią unitarną oraz | jest przestrzenią unitarną oraz | ||
<math> | <math>\|\cdot\|</math> jest normą zadaną przez iloczyn skalarny, | ||
to | to | ||
<br><center> | <br><center> | ||
<math> | <math>\forall x,y\in X: | ||
\bigg[ | \bigg[ | ||
x\perp y | x\perp y | ||
\ \ \Longleftrightarrow | \ \ \Longleftrightarrow\ | ||
\|x+y\|^{2} | \|x+y\|^{2} | ||
= | = | ||
\|x\|^{2}+\|y\|^{2} | \|x\|^{2}+\|y\|^{2} | ||
\bigg] | \bigg]</math> | ||
</math> | |||
<br></center> | <br></center> | ||
| Linia 1048: | Linia 969: | ||
{{dowod|3.29.|| | {{dowod|3.29.|| | ||
Dla dowolnych ustalonych <math> | Dla dowolnych ustalonych <math>x,y\in X</math> liczymy | ||
<br><center> | <br><center> | ||
<math> | <math>\|x+y\|^2 | ||
= | |||
\|x\|^2+2\underbrace{(x|y)}\limits_{=0}+\|y\|^2 | \|x\|^2+2\underbrace{(x|y)}\limits_{=0}+\|y\|^2 | ||
= | |||
\|x\|^2+\|y\|^2 | \|x\|^2+\|y\|^2</math>, | ||
</math> | |||
<br></center> | <br></center> | ||
co należało dowieść.<br> | co należało dowieść.<br> | ||
Zauważmy, że gdy <math> | Zauważmy, że gdy <math>X=\mathbb{R}^2</math>, to implikacja w prawą stronę w powyższym twierdzeniu <math>(\Rightarrow)</math>, to znane ze szkoły twierdzenie Pitagorasa. Implikację <math>(\Leftarrow)</math>, znamy ze szkoły, jako twierdzenie odwrotne do twierdzenia Pitagorasa. | ||
}} | }} | ||
Aktualna wersja na dzień 18:36, 12 wrz 2023
Norma. Iloczyn skalarny
W wykładzie tym wprowadzamy pojęcie normy i przestrzeni unormowanej. Pokazujemy, że kule w przestrzeniach unormowanych są zbiorami wypukłymi. Wprowadzamy pojęcia iloczynu skalarnego i przestrzeni unitarnej. Dowodzimy nierówność Schwarza, warunek równoległoboku i twierdzenie Pitagorasa.
Przestrzenie unormowane
Przypomnijmy, że na pierwszym wykładzie z Analizy Matematycznej 2 wprowadziliśmy pojęcie metryki, czyli funkcji, która każdym dwóm punktom danego zbioru przyporządkowuje ich odległość. W przypadku, gdy dany zbiór jest przestrzenią wektorową, możemy wprowadzić funkcję mierzącą "długość" wektora. Funkcję tę nazwiemy normą. Okaże się (zgodnie z intuicją, jak dla przypadku płaszczyzny ), że jeśli umiemy zmierzyć długość wektorów przestrzeni wektorowej , to możemy także mierzyć odległość między punktami zbioru .
Pojęcie normy jest szczególnie przydatne w przestrzeniach funkcji (np. przestrzeniach funkcji liniowych lub przestrzeniach funkcji ciągłych). Norma będzie nam również przydatna w przyszłości do zdefiniowania pochodnych wyższych rzędów dla funkcji wielu zmiennych.
Wprowadźmy formalną definicję (wektor zerowy przestrzeni wektorowej będziemy oznaczać przez ).
Definicja 3.1.
Niech będzie przestrzenią wektorową nad ciałem
( lub ).
Odwzorowanie
nazywamy normą w , jeśli:
(1)
;
(2)
(jednorodność);
(3)
(subaddytywność).
Parę nazywamy
przestrzenią unormowaną.
Zauważmy, że definicja powyższa precyzuje nasze naturalne
wymagania w stosunku do długości wektora, a mianowicie:
(1)
długość wektora wynosi zero wtedy i tylko wtedy, gdy wektor
jest zerowy;
(2)
długość iloczynu wektora przez liczbę, to iloczyn długości
tego wektora i wartości bezwzględnej tej liczby;
(3)
długość sumy wektorów jest nie większa od sumy ich długości.

Zobacz biografię
Przykład 3.2.
W przestrzeni wektorowej
nad możemy wprowadzić następujące
normy:
(norma euklidesowa),
(norma taksówkowa),
(normamaksimowa).
Dowód faktu, że powyższe odwzorowania są normami, pozostawiamy
na ćwiczenia (patrz ćwiczenie 3.1.).
Nazwy powyższych norm nie są przypadkowe
(patrz uwaga 3.4.).
Okazuje się, że każda przestrzeń unormowana jest w naturalny sposób przestrzenią metryczną. Mówi o tym następujące twierdzenie.
Twierdzenie 3.3.
Jeśli
jest przestrzenią unormowaną,
jest funkcją zadaną przez
,
to
jest przestrzenią metryczną.
Mówimy, że jest
metryką zadaną przez normę .
Dowód 3.3.
Załóżmy, że jest normą w .
Pokażemy, że odwzorowanie
zadane przez
jest metryką w .
(1)
Zauważmy, że dla dowolnych :
oraz
(2) Dla dowolnych mamy
(3) Dla dowolnych mamy
a więc zachodzi warunek trójkąta dla .
Pokazaliśmy zatem, że jest metryką.
(1)
Z powyższego twierdzenia wynika, że każda norma zadaje
metrykę.
(2)
Nie każda metryka jest zadana przez normę
(patrz wniosek 3.13.).
(3)
Zbieżność w sensie metryki zadanej przez normę nazywamy
zbieżnością silną lub
zbieżnością w normie, to znaczy
jeśli jest ciągiem, to
(4) Normy: euklidesowa, taksówkowa, maksimowa, zdefiniowane w przykładzie 3.2., zadają odpowiednio metryki: euklidesową, taksówkową, maksimową (patrz ćwiczenie 3.2.).
W przypadku norm można rozważać ich równoważność.
Definicja 3.5.
Dwie normy i w przestrzeni unormowanej nazywamy równoważnymi, jeśli
Równoważność norm ma następujące własności.
(1)
Relacja równoważności norm jest relacją
równoważnościową w zbiorze wszystkich norm na danej
przestrzeni unormowanej.
(2)
Normy: euklidesowa ; maksimowa taksówkowa są równoważne
(będzie to pokazane na ćwiczeniach; patrz ćwiczenie 3.3.).
Okazuje się, że w przestrzeniach wektorowych skończenie wymiarowych wszystkie normy są równoważne.
Twierdzenie 3.7.
Twierdzenie to podajemy tu bez dowodu. Wszystkie normy w są równoważne.
Kolejne twierdzenie mówi, że odwzorowanie normy jest ciągłe (oczywiście w przestrzeni rozważamy metrykę zadaną przez normę, a w metrykę euklidesową).
Twierdzenie 3.8.
Wszystkie normy w są równoważne.
Twierdzenie 3.9. [ciągłość normy]
Norma jest funkcją ciągłą, to znaczy
W dowodzie powyższego twierdzenia wykorzystamy następujący lemat, będący wariantem nierówności trójkąta.
Lemat 3.9.
Jeśli jest przestrzenią unormowaną, to
Dowód 3.9.
Korzystając z subaddytywności normy, dla dowolnych mamy
czyli
Analogicznie pokazujemy, że
Obie powyższe nierówności implikują nierówność w tezie lematu.
Dowód 3.8.
Warunek oznacza, że
Ustalmy dowolne . Z powyższej równości wynika, że
Zatem dla mamy
Zatem pokazaliśmy, że .
(1)
Implikacja odwrotna do implikacji w twierdzenieu 3.7. nie jest prawdziwa.
Aby to zobaczyć, rozważmy ciąg
zadany przez
.
Wówczas
ale sam ciąg nie jest silnie zbieżny
(dlaczego?)
(2)
Jeżeli granicą ciągu jest
(wektor "zerowy" przestrzeni wektorowej),
to implikację w twierdzenieu 3.7. można odwrócić, to znaczy zachodzi równoważność:
(dowód pozostawiamy jako proste ćwiczenie).
W przestrzeniach wektorowych możemy mówić o wypukłości zbiorów.
Definicja 3.11.
Niech będzie przestrzenią unormowaną oraz
.
(1)
Jeśli ,
to odcinkiem w łączącym punkty i
nazywamy zbiór
(2) Mówimy, że zbiór jest wypukły, jeśli
 |
 |
 |
W szczególnych przestrzeniach metrycznych, jakimi są przestrzenie unormowane, kule mają tę przydatną własność, że są wypukłe.
Twierdzenie 3.12.
Kule i kule domknięte w przestrzeniach unormowanych są
wypukłe.
 |
 |
 |
Dowód 3.12.
Niech oraz . Pokażemy, że kula jest zbiorem wypukłym. W tym celu wybierzmy dowolne . Z definicji kuli wynika, że
Niech . Należy pokazać, że . Z definicji odcinka w wiemy, że
Zatem
Zatem pokazaliśmy, że . Dowód, że jest zbiorem wypukłym, jest analogiczny.
Powyższe twierdzenie dostarcza nam pewnego warunku koniecznego na to, aby dana przestrzeń metryczna była zadana przez normę.
Wniosek 3.13.
Metryka kolejowa i metryka rzeka w nie są
zadane przez żadną normę, ponieważ kule w tych metrykach
nie są zbiorami wypukłymi
(patrz przykład 1.5. oraz przykład 1.6.).
Przypomnijmy, że przestrzeń metryczną nazywamy zupełną, gdy każdy ciąg Cauchy'ego tej przestrzeni ma granicę (patrz definicja 2.10.). Wśród przestrzeni unormowanych szczególną rolę odgrywają przestrzenie unormowane zupełne.

Zobacz biografię
Definicja 3.13. [przestrzeń Banacha]
Przestrzenią Banacha nazywamy przestrzeń unormowaną zupełną.
Przykład 3.14.
(1)
jest przestrzenią Banacha
(patrz wniosek 2.21.).
(2)
Przestrzeń
z normą
jest przestrzenią Banacha
(patrz ćwiczenie 3.5.).
Przestrzenie unitarne
W przestrzeniach wektorowych możemy wprowadzić pojęcie iloczynu skalarnego. Dzięki niemu będziemy mogli mówić o prostopadłości wektorów. Okaże się, że przestrzenie z iloczynem skalarnym są także przestrzeniami unormowanymi z naturalnie wprowadzoną normą.
Definicja 3.15.
Niech będzie rzeczywistą przestrzenią wektorową.
Odwzorowanie
nazywamy iloczynem skalarnym w , jeśli:
(1)
i ,
(2)
,
(3)
,
(4)
(symetria).
Parę nazywamy
przestrzenią unitarną.
(a) Warunki (2) i (3)
mówią, że iloczyn skalarny jest liniowy
ze względu na pierwszą zmienną.
(b) Ze względu na symetrię (4),
iloczyn skalarny jest także liniowy ze względu na drugą
zmienną, zatem jest on dwuliniowy.
Przykład 3.17
Odwzorowanie zdefiniowane przez
jest iloczynem skalarnym w . Nazywamy go standardowym iloczynem skalarnym w . Iloczyn ten znamy ze szkoły dla przestrzeni i .
Sprawdzimy kolejno punkty definicji iloczynu skalarnego.
(1)
Dla dowolnego mamy
oraz
(2) Dla dowolnych oraz mamy
(3) Dla dowolnych mamy
(4) Dla dowolnych mamy
Zatem pokazaliśmy, że odwzorowanie jest iloczynem skalarnym w .
Okazuje się, że przestrzeń z iloczynem skalarnym jest przestrzenią unormowaną.
Twierdzenie 3.18.
Jeśli
jest przestrzenią unitarną oraz
,
to
jest normą w .
Mówimy, że jest
normą zadaną przez iloczyn skalarny
.
W dowodzie wykorzystamy następującą nierówność Schwarza, zachodzącą w przestrzeniach unitarnych.
Lemat 3.19. [nierówność Schwarza]
Jeśli jest przestrzenią unitarną, to
Dowód 3.20.
Ustalmy dowolne . Jeśli to powyższa nierówność jest oczywistą równością. Załóżmy, że . Niech Korzystając z dwuliniowości iloczynu skalarnego, mamy:
Zatem mamy
skąd
a zatem
co należało dowieść.
Zauważmy, że nierówność Cauchy'ego (patrz lemat 3.8.) jest szczególnym przypadkiem nierówności Schwarza, gdy w przestrzeni mamy standardowy iloczyn skalarny.
Dowód 3.21.
(1)
a więc pierwszy warunek w definicji normy jest spełniony.
(2)
zatem drugi warunek (jednorodność) w definicji normy jest spełniony.
(3)
Korzystając z nierówności Schwarza, mamy
a więc
zatem trzeci warunek (subaddytywność) w definicji normy jest spełniony.
Przykład 3.22.
Podobnie jak dla przestrzeni unormowanych, tak i dla przestrzeni unitarnych szczególną rolę odgrywają przestrzenie unitarne zupełne.

Zobacz biografię
Definicja 3.23.
Przestrzenią Hilberta nazywamy przestrzeń unitarną zupełną.
Twierdzenie 3.24. [ciągłość iloczynu skalarnego]
Iloczyn skalarny w przestrzeni unitarnej jest funkcją ciągłą, to znaczy
(oczywiście zbieżność oznacza zbieżność w normie zadanej przez iloczyn skalarny ).
Dowód 3.24. [dowód nadobowiązkowy]
Niech będzie ciągiem takim, że i . Oznacza to, że
oraz z ciągłości normy (patrz twierdzenie 3.7.), mamy
Korzystając z nierówności Schwarza, mamy
Z wyżej wskazanych zbieżności w wynika, że prawa strona nierówności, a zatem także lewa, zmierza do zera, gdy . Oznacza to, że , co należało dowieść.
W przestrzeni unitarnej możemy wprowadzić pojęcie prostopadłości wektorów.
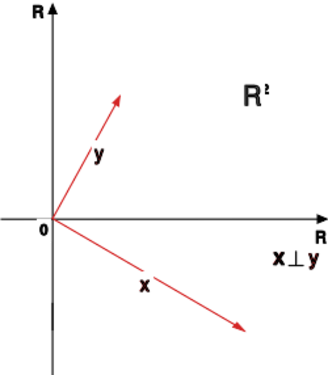 |
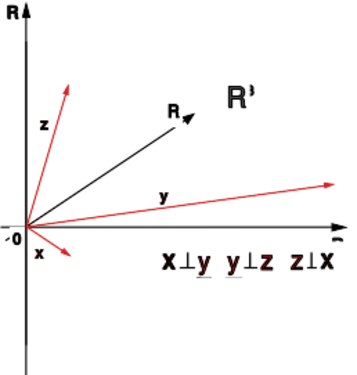 |
Definicja 3.25.
Niech będzie przestrzenią
unitarną.
(1)
Jeśli , to mówimy, że wektory
i są ortogonalne (lub prostopadłe)
i piszemy .
(2) Niech będzie podprzestrzenią wektorową . Mówimy, że wektor jest ortogonalny (prostopadły, normalny) do podprzestrzeni , jeśli
Piszemy .
(3) Mówimy, że wektory tworzą układ ortogonalny, jeśli
(4) Mówimy, że wektory tworzą układ ortonormalny, jeśli
(to znaczy wektory są parami ortogonalne oraz mają normę ).
Poniższe twierdzenie podamy tu bez dowodu.
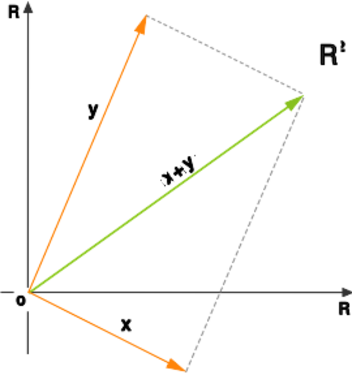
Twierdzenie 3.26.
Każda przestrzeń unitarna skończenie wymiarowa posiada bazę ortonormalną (to znaczy bazę tworzącą układ ortonormalny).
Przykład 3.27.
Baza kanoniczna w jest bazą ortonormalną.
Twierdzenie 3.28. [warunek równoległoboku]
Jeśli jest przestrzenią unitarną oraz jest normą zadaną przez iloczyn skalarny, to
Dowód 3.28.
Dla dowolnych ustalonych liczymy
,
oraz
Dodając stronami powyższe równości, dostajemy tezę twierdzenia.

Zobacz biografię
Twierdzenie 3.29. [Twierdzenie Pitagorasa]
Jeśli jest przestrzenią unitarną oraz jest normą zadaną przez iloczyn skalarny, to
Dowód 3.29.