Teoria kategorii dla informatyków/Wykład 9: Sprzężenia I

Pojęcie sprzężenia jest jednym z najważniejszych w kursie teorii kategorii. Sprzężenie jest pewną prostą zależnością pomiędzy dwoma przeciwnie zwróconymi funktorami, która, jak się okazuje, występuje niezwykle często w matematyce.

Definicja 9.1 [sprzężenie I]

Dwa funktory $F:\mathbf{𝐗}\to \mathbf{𝐀}$ i $G:\mathbf{𝐀}\to \mathbf{𝐗}$

tworzą sprzężenie, jeśli dla dowolnej pary obiektów $X\in {\mathbf{𝐗}}_0,A\in {\mathbf{𝐀}}_0$ istnieje naturalna bijekcja:

${\varphi }_{X,A}:\mathbf{𝐗}(FX,A)\cong \mathbf{𝐀}(X,GA)$

W takim wypadku $F$ nazywamy lewym sprzężeniem, $G$ nazywamy prawym sprzężeniem i całą sytuację opisujemy krótko jako:

$F⊣G$

Taka definicja wyjaśnia dobrze ideę sprzężenia, ale szczegóły trzeba rozszyfrować: naturalność bijekcji ${\varphi }_{X,A}$ oznacza, że $\varphi$ jest naturalnym izomorfizmem pomiędzy pewnymi funktorami (dociekliwym należy się wyjaśnienie, że oba te funktory są typu ${\mathbf{𝐗}}^{op}\times \mathbf{𝐀}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$), a naturalność $\varphi$, pomijając nieciekawe przekształcenia techniczne, sprowadza się ni mniej, ni więcej do faktu, że poniższe dwa diagramy komutują dla dowolnych morfizmów $k:A\to A^{\prime }\in {\mathbf{𝐀}}_1$ i $h:X\to X^{\prime }\in {\mathbf{𝐗}}_1$:

Równoważnie do Definicji 9.1 powiemy więc, że:

Definicja 9.2

Dwa funktory $F:\mathbf{𝐗}\to \mathbf{𝐀}$ i $G:\mathbf{𝐀}\to \mathbf{𝐗}$ tworzą sprzężenie, jeśli dla dowolnej pary obiektów $X\in {\mathbf{𝐗}}_0,A\in {\mathbf{𝐀}}_0$ istnieje naturalna bijekcja (piszmy niepoprawnie $\varphi$ zamiast uciążliwego ${\varphi }_{X,A}$), która dowolnej strzałce $f:FX\to A$ przypisuje strzałkę $\varphi (f):X\to GA$ tak, że $\varphi (k\circ f)=G(k)\circ \varphi (f)$ oraz $\varphi (f\circ F(h))=\varphi (f)\circ h$ dla dowolnych strzałek $k:A\to A^{\prime }$ i $h:X\to X^{\prime }$.

Wkrótce wykażemy, że jeśli funktor $G$ ma lewe sprzężenie $F$ (tzn. istnieje funktor $F$ taki, że $F⊣G$), to $F$ jest jedyny z dokładnością do izomorfizmu (tzn. $(F⊣G\wedge H⊣G)\Rightarrow F\cong H$). Istnienie lewego lub prawego sprzężenia jest często ciekawym problemem matematycznym i jeśli da się udowodnić, sam dowód jest pożyteczną konstrukcją. Nie ma potrzeby dłużej strzępić języka, zobaczmy przykłady.

• Wolne funktory są lewymi sprzężeniami do funktorów zapominania. Np. jeśli $G$ jest grupą, zaś $X$ jest zbiorem, to funkcje $X\to G$ są w bijekcji z homomorfizmami typu $F(X)\to G$, gdzie $F(X)$ jest wolną grupą nad $X$. A zatem $F⊣U$, gdzie $U:\mathbf{𝐆}\mathbf{𝐫}\mathbf{𝐩}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ jest funktorem zapominania, zaś $F:\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}\to \mathbf{𝐆}\mathbf{𝐫}\mathbf{𝐩}$ jest funktorem tworzącym wolną grupę nad $X$. Inny przykład tego typu znajduje się w Zadaniu 9.1.

Uwaga

Problem istnienia lewego sprzężenia do funktora zapominania $U:\mathbf{𝐂}\to \mathbf{𝐃}$ jest w zasadzie pytaniem o to, jak w sposób jednorodny zadać strukturę wymaganą przez $\mathbf{𝐂}$ na obiektach i strzałkach $\mathbf{𝐃}$. Pytania o lewe sprzężenie są więc pytaniami typu: w jaki sposób na dowolnym zbiorze zadać topologię? Czy dla dowolnego zbioru da się znaleźć działanie grupowe tak, by elementy tego zbioru były elementami powstałej grupy? Czy każda przestrzeń metryczna da się rozszerzyć do przestrzeni zupełnej? I tak dalej. Niezwykle interesującą klasą kategorii, które posiadają lewe sprzężenie do funktora zapominania z kodziedziną w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ są tzw. kategorie algebraiczne. Mówimy o nich więcej w Wykładzie 15.

• Przypuśćmy, że $\mathbf{𝐂}$ jest kategorią kartezjańsko zamkniętą. Niech $X\in {\mathbf{𝐂}}_0$. Wówczas funktor:

$[X,-]:\mathbf{𝐂}\to \mathbf{𝐂}$

jest lewym sprzężeniem funktora $-\times X:\mathbf{𝐂}\to \mathbf{𝐂}$ (przypomnijmy sobie definicje pierwszego z tych funktorów podaną w Zadaniu 4.1 - definicja drugiego jest oczywista po przeczytaniu Zadania 3.6), co oznacza, że istnieje naturalna bijekcja pomiędzy morfizmami typu $Z\times X\to Y$ i morfizmami typu $Z\to [X,Y]$ (dla $Y,Z\in {\mathbf{𝐂}}_0$).

• Jeśli $\mathbf{𝐉},\mathbf{𝐂}$ są dowolnymi kategoriami, to funktor diagonalny $\mathrm{\Delta }:\mathbf{𝐂}\to [\mathbf{𝐉},\mathbf{𝐂}]$ jest lewym sprzężeniem do funktora $\underset{\leftarrow \mathbf{𝐉}}{\lim }:[\mathbf{𝐉},\mathbf{𝐂}]\to \mathbf{𝐂}$. Rzeczywiście, wprost z Zadania 8.1, obiekt $X\in {\mathbf{𝐂}}_0$ jest granicą diagramu $D:J\to \mathbf{𝐂}$ wtedy i tylko wtedy, gdy istnieje naturalny izomorfizm:

$[J,\mathbf{𝐂}](\mathrm{\Delta }X,D)\cong {\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}}_{\mathbf{𝐂}}(X,D)\cong \mathbf{𝐂}(X,\underset{\leftarrow \mathbf{𝐉}}{\lim }D)$

A zatem $\mathrm{\Delta }⊣\underset{\leftarrow \mathbf{𝐉}}{\lim }$. Szczególne przypadki tego sprzężenia omówimy w Zadaniach 9.2, 9.3.

• Dla posetów $P,Q$ para funkcji monotonicznych $r:P\to Q$, $s:Q\to P$ jest sprzężeniem wtedy i tylko wtedy, gdy

$\mathrm{\forall }x\in P\mathrm{\forall }y\in Q(x\le s(y)⟺r(x)\le y)$

Na przykład, inkluzja $U:(\mathbb{\mathbb{Z}},\le )\to (\mathbb{ℝ},\le )$ posiada lewe sprzężenie, które powszechnie nazywa się funkcją sufit $\lceil \cdot \rceil :\mathbb{ℝ}\to \mathbb{\mathbb{Z}}$}:

Parser nie mógł rozpoznać (błąd składni): {\displaystyle \lceil x\rceil := \mathrm{najmniejsza\ liczba\ całkowita} \geq x}

Rzeczywiście, równoważność definiująca sprzężenie:

$x\le U(y)⟺\lceil x\rceil \le y$

zachodzi wtedy i tylko wtedy, gdy $\lceil x\rceil$ jest najmniejszą liczbą całkowitą większą bądź równą $x$.

• Dualność Stone'a (patrz Ćwiczenia do Wykładu 6.). Twierdzenie Stone'a jest jednym z najważniejszych wyników matematyki XX wieku. W ograniczonym brzmieniu (tj. dualność między algebrami Boole'a a przestrzeniami Stone'a) udowodnione przez Marshalla Stone'a w 1939 roku, twierdzenie to po raz pierwszy jednoznacznie potwierdziło użyteczność metod topologii ogólnej w algebrze i dało początek topologii algebraicznej. Wspaniałe omówienie roli dualności Stone'a znajduje się w książce Stone Spaces P.T.Johnstone'a (Cambridge University Press, 1982).

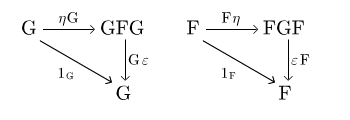
Wracając do głównego wątku wykładu, zanalizujmy głębiej strukturę sprzężenia. Przy ustalonych oznaczeniach z Definicji 9.2 (pominiemy też wszelkie zbędne nawiasy) zauważmy, że jeśli przyjmiemy $A=F(X)$, to $1_X\in \mathbf{𝐀}(FX,FX)$. Możemy więc położyć dla każdego $X\in \mathbf{𝐗}$ morfizm typu $X\to GFX$:

${\eta }_X:=\varphi (1_{FX})$

Sama operacja $\eta$, która obiektowi $X$ przypisuje strzałkę ${\eta }_X$ jest transformacją naturalną typu $1_{\mathbf{𝐗}}\to GF$, ponieważ każdy diagram:

komutuje. Rzeczywiście,

$GFh\circ {\eta }_X=GFh\circ \varphi (1_{FX})=\varphi (Fh\circ 1_{FX})=\varphi (1_{F{X}^{\prime }}\circ Fh)=\varphi (1_{F{X}^{\prime }})\circ h={\eta }_{X^{\prime }}\circ h$

gdzie dwukrotnie wykorzystaliśmy naturalność $\varphi$. Transformację $\eta$ nazywamy jednością sprzężenia $F⊣G$.

Pokażemy teraz, że bijekcja

$\varphi$

może być całkowicie odtworzona za pomocą

$\eta$

, to znaczy, że kolekcja komponentów

$\{{\eta }_X{\}}_{X\in \mathbf{𝐗}}$

wystarcza do zrekonstruowania bijekcji

$\varphi$

. Niech

$f:FX\to A$

. Wówczas

${\varphi }_{X,A}(f)=\varphi (f\circ 1_{FX})=Gf\circ \varphi (1_{FX})=Gf\circ {\eta }_X$

. Warto zapamiętać:

${\varphi }_{X,A}(f)=Gf\circ {\eta }_X$      (9.1)

Dualnie, jeśli przyjmiemy w Definicji 9.2, że $X=GA$, to możemy zdefiniować dla każdego $A\in \mathbf{𝐀}$ strzałkę ${\epsilon }_A:FGA\to A$:

${\epsilon }_A:={\varphi }^{-1}(1_{GA})$

Transformację naturalną

$\epsilon$

nazywamy kojednością sprzężenia

$F⊣G$

. Mając na uwadze, że

${\varphi }^{-1}(g\circ h)={\varphi }^{-1}(g)\circ Fh$

oraz

${\varphi }^{-1}(Gk\circ g)=k\circ {\varphi }^{-1}(g)$

dla dowolnej

$g\circ X\to GA$

mamy:

${\varphi }^{-1}(g):={\epsilon }_A\circ Fg$      (9.2)

co oznacza, że kojedność wystarcza do odtworzenia

${\varphi }^{-1}$

, a co za tym idzie,

$\varphi$

.

W końcu, zauważmy, że:

$G({\epsilon }_A)\circ {\eta }_{GA}=\varphi ({\epsilon }_A\circ {\eta }_{FGA})=\varphi ({\epsilon }_A)=\varphi ({\varphi }^{-1}(1_{GA}))=1_{GA}$

i podobnie:

${\epsilon }_{FX}\circ F({\eta }_X)={\varphi }^{-1}({\eta }_X)={\varphi }^{-1}(\varphi (1_{FX}))=1_{FX}$

Pokazaliśmy najważniejsze kroki następującego twierdzenia:

Twierdzenie 9.3

Następujące warunki są równoważne:

• $F⊣G$,
• Istnieją dwie transformacje naturalne $\eta :1_{\mathbf{𝐗}}\to GF$ i $\epsilon :FG\to 1_{\mathbf{𝐀}}$ takie, że następujące diagramy trójkątne komutują:

Uwaga

aby w pełni zrozumieć treść powyższego twierdzenia, należy zauważyć, że transformacje naturalne można złożyć z funktorami (i to na dwa sposoby). Na przykład, $\eta G$ jest transformacją naturalną będącą złożeniem transformacji $\eta$ i funktora $G$. To złożenie definiujemy przez komponenty jako $(\eta G{)}_A:={\eta }_{GA}$; podobnie $G\eta$ jest transformacją naturalną daną przez komponenty $(G\eta {)}_A:=G({\eta }_A)$. I tak dalej. Uważny czytelnik powinien udowodnić, że złożenia, które tu opisujemy są rzeczywiście transformacjami naturalnymi.

Przejdźmy do ostatniej charakteryzacji sprzężenia, które uwypukla uniwersalny charakter jedności sprzężenia. Przypomnijmy sobie definicję elementu uniwersalnego dla funktora reprezentowalnego $F:{\mathbf{𝐂}}^{op}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ (Definicja 7.4): element $e\in F$ jest uniwersalny jeśli dla każdego obiektu $Y\in {\mathbf{𝐂}}_0$ i elementu $y\in FY$ istnieje dokładnie jedna funkcja $f:Y\to X$ taka, że $F(f)(e)=y$. Ale $e$ może być traktowany jako strzałka $\mathbf{𝟏}\to FX$ w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ ($\mathbf{𝟏}$ jest dowolnym singletonem - obiektem końcowym $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$), Definicja elementu uniwersalnego może być więc uogólniona i postawiona dla funktorów dowolnego typu:

Definicja 9.4

Niech $F:\mathbf{𝐃}\to \mathbf{𝐂}$ będzie funktorem i niech $C\in {\mathbf{𝐂}}_0$. Strzałką uniwersalną z $C$ do $F$ jest para $(X,e)$ składająca się z obiektu $X\in {\mathbf{𝐂}}_0$ i strzałki $e:C\to FX\in {\mathbf{𝐂}}_1$ taka, że dla dowolnego obiektu $Y\in {\mathbf{𝐂}}_0$ i strzałki $y:C\to FX$ istnieje dokładnie jedna strzałka $f:X\to Y$ spełniająca $Ff\circ e=y$.

Innymi słowy: każda strzałka $y$ faktoryzuje się przez $e$.

Jak się okazuje, sprzężenie jest w pełni scharakteryzowane przez fakt, że jedność ${\eta }_X$ jest strzałką uniwersalną z $X$ do $G$ (przy oznaczeniach Definicji 9.2).

Twierdzenie 9.5

Następujące warunki są równoważne:

• $F⊣G$
• $\eta :1_{\mathbf{𝐗}}\to GF$ jest transformacją naturalną taką, że dla każdego $X\in {\mathbf{𝐂}}_0$, ${\eta }_X$ jest strzałką uniwersalną z $X$ do $G$.

Dowód

Strzałka ${\eta }_X$ jest uniwersalna wtedy i tylko wtedy, gdy dla dowolnego morfizmu $f:X\to GA$ istnieje dokładnie jeden morfizm $g:FX\to A$ tak, że następujący diagram komutuje: Ale to oznacza, że $\theta (g):=Gg\circ {\eta }_X$ jest bijekcją pomiędzy $\mathbf{𝐀}(FX,A)$ i $\mathbf{𝐗}(X,GA)$. Ta bijekcja jest naturalna względem $X$, bo $\eta$ jest naturalna; jest naturalna względem $A$, bo $G$ jest funktorem. To dowodzi $F⊣G$.

Uwaga: Powyższe twierdzenie jest jednym z najpopularniejszych sposobów prezentowania sprzężenia. Śmiało możemy więc ująć je jako definicję:

Definicja 9.6 [Sprzężenie II]

Dla $F:\mathbf{𝐗}\to \mathbf{𝐀}$ i $G:\mathbf{𝐀}\to \mathbf{𝐗}$ mamy $F⊣G$ wtedy tylko wtedy, gdy dla każdego $X\in {\mathbf{𝐗}}_0$ istnieje strzałka ${\eta }_X:X\to GFX$ taka, że: dla dowolnego morfizmu $f:X\to GA$ istnieje dokładnie jeden morfizm $g:FX\to A$ tak, że następujący diagram komutuje:

Oto dalsze przykłady sprzężeń:

• Funktor $\mathrm{L}\mathrm{i}\mathrm{s}\mathrm{t}:\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}\to \mathbf{𝐌}\mathbf{𝐨}\mathbf{𝐧}$ (patrz Przykład 5.3) jest lewym sprzężeniem do funktora zapominania $U:\mathbf{𝐌}\mathbf{𝐨}\mathbf{𝐧}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ (bo $\mathrm{L}\mathrm{i}\mathrm{s}\mathrm{t}$ jest funktorem wolnym). Dla zbioru $X$ jedność sprzężenia ${\eta }_X:X\to \mathrm{L}\mathrm{i}\mathrm{s}\mathrm{t}(X)$ jest funkcją $x\mapsto [x]$, czyli przekształca elementy $X$ na listy jednoelementowe. W tym przykładzie, dla funkcji $f:X\to \mathbb{\mathbb{N}}$, $f(x):=1$ jedyną funkcją (oznaczoną $l$), która sprawia, że diagram:

komutuje, jest funkcja przypisująca liście jej długość.

• Niech $\mathbf{𝐌}\mathbf{𝐞}\mathbf{𝐭}$ oznacza kategorię przestrzeni metrycznych i funkcji niepowiększających odległości, zaś $\mathbf{𝐂}\mathbf{𝐌}\mathbf{𝐞}\mathbf{𝐭}$ - kategorię przestrzeni metrycznych zupełnych, z takimi samymi morfizmami. Wówczas dla funktora zapominania $U:\mathbf{𝐂}\mathbf{𝐌}\mathbf{𝐞}\mathbf{𝐭}\to \mathbf{𝐌}\mathbf{𝐞}\mathbf{𝐭}$ istnieje lewe sprzężenie, które każdej przestrzeni metrycznej przypisuje jej uzupełnienie. Jednością tego sprzężenia jest rodzina odwzorowań, które elementowi $x$ przestrzeni metrycznej $X$ przypisują stały ciąg Cauchy'ego $(x,x,x,...)$.

W Ćwiczeniach do tego wykładu omówimy szczegółowo zarówno przykłady, które już się pojawiły, jak i całkiem nowe, często być może zaskakujące Czytelnika sytuacje, których ukrytym mechanizmem jest sprzężenie.