Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne
Przestrzenie metryczne
Ten wykład poświęcony jest pojęciu przestrzeni metrycznej. Prezentujemy definicję metryki i przykłady przestrzeni metrycznych. Definiujemy zbiory otwarte, domknięte, punkty skupienia i średnicę zbioru. Następnie wprowadzamy pojęcia zwartości i spójności w przestrzeniach metrycznych. Dowodzimy, że przedział domknięty i ograniczony jest zbiorem zwartym w oraz charakteryzujemy zbiory spójne w .
Jedną z najistotniejszych idei matematyki jest idea aproksymacji. Z aproksymacją mamy do czynienia wtedy, gdy pewien obiekt (liczbę, funkcję, zbiór) przedstawiamy jako granicę (w odpowiednim sensie) ciągu obiektów . Możemy wtedy wnioskować o własnościach "mniej znanego" obiektu z własności "bardziej znanych" obiektów . Każdy z nas zetknął się z aproksymacją, chociażby w stwierdzeniu " wynosi mniej więcej " (tu przybliżamy liczbę niewymierną ciągiem liczb wymiernych). Na wykładzie poświęconym ciągom funkcyjnym dowiemy się, że jeśli funkcja jest granicą (w specjalnym sensie) ciągu funkcji ciągłych to jest funkcją ciągłą. Ponieważ mamy wiele różnych rodzajów zbieżności (czyli przejść granicznych) potrzebna jest w matematyce w miarę ogólna, a zarazem prosta teoria przechodzenia do granicy. O podstawach tej teorii opowiemy na dwóch pierwszych wykładach poświęconych przestrzeniom metrycznym i ciągom w przestrzeniach metrycznych. Na trzecim wykładzie zajmiemy się działem teorii przestrzeni metrycznych - przestrzeniami unormowanymi. Teoria ta pozwala dodatkowo "przenieść" do teorii granic ważne idee geometryczne związane z działaniami na wektorach.
Metryka
Przypomnijmy, że różne sposoby mierzenia odległości w poznaliśmy na wykładzie z Analizy matematycznej 1. Tam też zapoznaliśmy się z pojęciem metryki. Okazuje się, że funkcję zwaną metryką można zdefiniować dla dowolnego (niepustego) zbioru (a nie tylko dla ). W ten sposób będziemy mogli mierzyć odległości między elementami dowolnego zbioru .
Definicja 1.1. [metryka, odległość]
Niech
będzie zbiorem niepustym.
Metryką w zbiorze nazywamy dowolną
funkcję
spełniającą następujące warunki:
(i)
;
(ii)
(warunek symetrii);
(iii)
(warunek trójkąta).
Parę nazywamy
przestrzenią metryczną.
Dla dowolnych ,
liczbę nazywamy
odległością
punktów i
oraz mówimy, że punkty i są
oddalone od siebie o .
Definicja kuli w dowolnej przestrzeni metrycznej jest analogiczna do poznanej na wykładzie z Analizy Matematycznej 1 definicji kuli w .
Definicja 1.2. [kula, kula domknięta]
Niech będzie przestrzenią metryczną. Kulą o środku w punkcie i promieniu nazywamy zbiór:
Kulą domkniętą o środku w punkcie i promieniu nazywamy zbiór:
Podamy teraz kilka przykładów przestrzeni metrycznych oraz opiszemy, jak wyglądają kule w tych przestrzeniach.
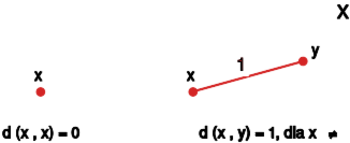
Przykład 1.3. [Metryka dyskretna]
Niech będzie dowolnym zbiorem oraz niech
Zauważmy, iż wartość funkcji dla dwóch dowolnych punktów
wynosi , gdy są one różne oraz wynosi , gdy jest to ten sam
punkt.
Łatwo sprawdzić, że tak zdefiniowana funkcja jest metryką, zatem para jest przestrzenią metryczną. Metrykę tę będziemy nazywali metryczną dyskretną. Faktycznie, z definicji wynika, że dla dowolnych mamy
oraz
Dla sprawdzenia warunku trójkąta weźmy . Rozważymy następujące przypadki.
1) Jeśli , to zatem zawsze zachodzi .
2) Jeśli , to lub . Wtedy również .
Łatwo także zauważyć, jak będą wyglądały kule w tej przestrzeni metrycznej. Jeśli , to kula o promieniu składa się z samego środka, ale jeśli , to kulą jest cała przestrzeń . Mamy zatem
Zatem w przestrzeni metrycznej dyskretnej kulami i kulami domkniętymi są jedynie:
, zbiory jednopunktowe oraz cała przestrzeń.
Przypomnijmy teraz standardowe metryki w .
Były one wprowadzone na wykładzie z Analizy Matematycznej 1.

Zobacz biografię
Przykład 1.4. [Metryka maksimowa, taksówkowa i euklidesowa]
Niech oraz niech
,
gdzie oraz .
Para jest przestrzenią metryczną.
Funkcję nazywamy
metryką maksimową w .
Para jest przestrzenią metryczną.
Funkcję nazywamy
metryką taksówkową w .
Para jest przestrzenią metryczną.
Funkcję nazywamy
metryką euklidesową w ,
zaś parę nazywamy
przestrzenią metryczną euklidesową.
Dwa kolejne przykłady podają mniej typowe metryki na płaszczyźnie .
Przykład 1.5. [Metryka rzeka]
Wyobraźmy sobie, że płaszczyzna jest gęstym lasem oraz pewna prosta jest rzeką. Aby zmierzyć odległość dwóch punktów , musimy wyciąć ścieżkę od do , przy czym możemy to robić tylko prostopadle do rzeki.
Mamy dwa przypadki:
(1)
Jeśli punkty i są końcami odcinka prostopadłego do
rzeki , to ich odległość jest równa zwykłej odległości
euklidesowej na płaszczyźnie.
(2)
Jeśli zaś punkty i nie leżą na prostej prostopadłej do
rzeki , to musimy utworzyć dwie ścieżki jedną od punktu
do rzeki,
a drugą od rzeki do punktu ,
zawsze prostopadle do rzeki.
Teraz odległość od do będzie równa długości
(euklidesowej) obu ścieżek oraz odległości tych ścieżek na
rzece.
Nietrudno sprawdzić, że tak utworzona funkcja jest metryką w
.
Przykład 1.6. [Metryka kolejowa]
Wyobraźmy sobie, że na płaszczyźnie wyróżniony jest jeden punkt
, węzeł kolejowy, od którego odchodzą półproste,
szyny, we wszystkich kierunkach.
Aby zmierzyć odległość miedzy dwoma punktami i ,
musimy przebyć drogę między nimi, poruszając się po
szynach. Rozważmy dwa przypadki:
(1) Jeśli punkty i znajdują się na wspólnej
półprostej wychodzącej z punktu , to ich odległość jest
zwykłą odległością euklidesową.
(2) Jeśli zaś punkty i nie leżą na wspólnej półprostej
wychodzącej z punktu to ich odległość jest równa sumie
odległości euklidesowych od do
oraz od do .
Tak wprowadzona funkcja odległości jest metryką,
Zdefiniujemy teraz pewne pojęcia związane z przestrzeniami metrycznymi. Część z nich była zdefiniowana na Analizie Matematycznej 1.
Definicja 1.7.
Niech będzie przestrzenią metryczną, niech
oraz .
(1)
Zbiór nazywamy otwartym, jeśli
każdy punkt zbioru zawiera się w
wraz z pewną kulą, czyli
(2)
Punkt nazywamy
punktem wewnętrznym zbioru , jeśli istnieje
kula o środku w punkcie (i dodatnim promieniu)
taka, że zawiera się w .
Wnętrzem zbioru nazywamy zbiór jego punktów wewnętrznych
i oznaczamy go .
(3)
Domknięciem zbioru nazywamy zbiór
wszystkich punktów oraz wszystkich punktów skupienia zbioru
i oznaczamy go .
(4) Brzegiem zbioru nazywamy zbiór
.
Przykład 1.8.
W przestrzeni metrycznej dyskretnej każdy zbiór jest otwarty, bo wraz z każdym punktem zawiera kulę .
Przykład 1.9.
W przestrzeni z metryką euklidesową rozważmy zbiór . Wówczas
Podobnie jak w tak i w dowolnej przestrzeni metrycznej zachodzą następujące własności.
Twierdzenie 1.10. [Zbiory w przestrzeniach metrycznych]
Jeśli
jest przestrzenią metryczną,
to
(1)
Każda kula jest zbiorem otwartym w .
(2)
Zbiór jest otwarty, wtedy i tylko wtedy, gdy
(dopełnienie zbioru ) jest zbiorem domkniętym.
(3)
Kula domknięta jest zbiorem domkniętym.
(4)
Jeśli jest punktem skupienia zbioru ,
to dowolna kula o środku w punkcie
(i dodatnim promieniu) zawiera nieskończenie wiele
punktów zbioru .
(5) Suma dowolnej rodziny zbiorów otwartych jest
zbiorem otwartym.
(6) Przecięcie (część wspólna) skończonej rodziny
zbiorów otwartych jest zbiorem otwartym.
(7) Przecięcie (część wspólna) dowolnej rodziny
zbiorów domkniętych jest zbiorem domkniętym.
(8) Suma skończonej rodziny
zbiorów domkniętych jest zbiorem domkniętym.
(9) Dla dowolnego zbioru
, zbiór (domknięcie zbioru ) jest zbiorem
domkniętym.
Omówienie i przykłady powyższych własności mieliśmy na wykładzie z Analizy Matematycznej 1 (patrz Analiza matematyczna 1 przykład 3.15.).
Kolejne pojęcia związane z przestrzeniami metrycznymi podane są w poniższej definicji.
Definicja 1.11.
(1) Srednicą zbioru nazywamy liczbę:
(2) Odległością punktu od zbioru nazywamy liczbę:
(3)
Mówimy, że zbiór jest
ograniczony, jeśli jest zawarty w pewnej kuli,
to znaczy
| [[File:AM1.M03.W.R17.svg|253x |
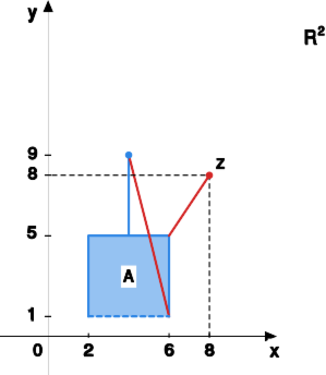
Przykład 1.12.
Na płaszczyźnie z metryką euklidesową rozważmy zbiór
oraz punkt . Wyznaczyć średnicę zbioru oraz odległość punktu od zbioru .
Z poniższego rysunku widzimy, że
oraz .Przykład 1.13.
Niech będzie przestrzenią metryczną dyskretną. Jeśli , to , a jeśli , to . Zatem każdy zbiór w metryce dyskretnej jest ograniczony.
Następujące oczywiste twierdzenie podaje związek między ograniczonością zbioru oraz jego średnicą.
Twierdzenie 1.14.
Jeśli jest przestrzenią metryczną, , to zbiór jest ograniczony wtedy i tylko wtedy, gdy .
W iloczynie kartezjańskim przestrzeni metrycznych można także
zadać metrykę
(tak zwaną metrykę produktową) na kilka naturalnych
sposobów.
Poniższe twierdzenie podaje jeden z takich sposobów.
[[grafika:Kartezjusz.jpg|thumb|right||Kartezjusz (1596-1650)
Zobacz biografię]]
Twierdzenie 1.15. [Iloczyn kartezjański przestrzeni metrycznych]
Jeśli są przestrzeniami metrycznymi dla jest funkcją zdefiniowaną przez
,
to
jest przestrzenią metryczną.
Wówczas nazywamy
metryką produktową lub
metryką standardową w iloczynie kartezjańskim
.
Dowód 1.15.
Dowód oparty na nierówności Cauchy'ego (patrz Analiza matematyczna 1 lemat 3.8.) jest analogiczny do dowodu, że jest metryką w (porównaj Analiza matematyczna 1 przykład 3.7. i lemat 3.9.).
Metryka euklidesowa w jest metryką standardową w . Wynika to wprost z definicji obu metryk.
Jeśli jest przestrzenią metryczną oraz , to zbiór jest także przestrzenią metryczną z metryką . Kule w przestrzeni są równe przecięciom kul z przestrzeni ze zbiorem . Metrykę na nazywamy metryką indukowaną. W przyszłości o podzbiorach przestrzeni metrycznej będziemy także mówili "przestrzeń metryczna".
Zwartość
Wprowadzimy teraz ogólniejsze pojęcie zwartości niż to, z którym spotkaliśmy się na wykładzie z Analizy Matematycznej 1 (patrz Analiza matematyczna 1 definicja 8.21.).
Definicja 1.18.
Niech będzie przestrzenią metryczną oraz
(1)
Pokryciem otwartym
zbioru nazywamy dowolną rodzinę
zbiorów otwartych taką, że
.
Pokrycie to nazywamy skończonym,
jeśli
.
(2)
Mówimy, że jest
podpokryciem
pokrycia zbioru , jeśli
jest pokryciem zbioru oraz
.
(3)
Mówimy, że zbiór jest zwarty, jeśli z każdego
pokrycia otwartego zbioru można wybrać pokrycie
skończone.
Kolejne twierdzenie zbiera pewne informacje dotyczące zbiorów zwartych w przestrzeniach metrycznych.
Twierdzenie 1.19.
W dowolnej przestrzeni metrycznej mamy
(1)
Zbiór skończony jest zwarty.
(2)
Podzbiór zwarty przestrzeni metrycznej jest domknięty.
(3)
Podzbiór zwarty przestrzeni metrycznej jest ograniczony.
(4)
Podzbiór domknięty zbioru zwartego jest zwarty.
(5)
Część wspólna zbioru zwartego i domkniętego jest zbiorem
zwartym.
Dowód 1.19. [nadobowiązkowy]
(Ad (1)) Niech będzie zbiorem skończonym w i niech będzie pokryciem otwartym zbioru . Z definicji pokrycia mamy w szczególności
Zatem
.
Pokazaliśmy zatem, że
jest podpokryciem (skończonym)
pokrycia zbioru .
(Ad (2))
Niech będzie zwartym podzbiorem w .
Wystarczy pokazać, że jest zbiorem otwartym
(patrz twierdzenie 1.10. (6)).
W tym celu niech .
Dla dowolnego niech
.
Wówczas oraz
.
Rodzina jest pokryciem otwartym zbioru
.
Ponieważ jest zbiorem zwartym, więc możemy z tego pokrycia
wybrać podpokrycie skończone,
powiedzmy
,
zatem
Niech .
Wówczas jest kulą o środku w punkcie taką,
że ,
czyli jest punktem wewnętrznym zbioru .
Pokazaliśmy więc, że zbiór jest otwarty,
a zatem zbiór jest domknięty.
(Ad (3))
Niech będzie zwartym podzbiorem w .
Należy pokazać, że zbiór jest ograniczony.
Niech będzie dowolnym punktem.
Zauważmy, że
to znaczy rodzina kul jest pokryciem otwartym zbioru . Z zwartości zbioru wynika, iż z tego pokrycia można wybrać podpokrycie skończone, to znaczy
Ale ciąg kul jest wstępujący, a więc
zatem zbiór jest ograniczony.
(Ad (4)) Niech będzie domkniętym podzbiorem zbioru
zwartego .
Niech będzie dowolnym pokryciem zbioru .
Ponieważ jest domknięty, więc
jest zbiorem otwartym
(patrz twierdzenie 1.10. (6)).
Niech , będzie nowym indeksem
oraz zdefiniujmy .
Niech .
Wówczas
zatem jest pokryciem zbioru .
Ponieważ zbiór jest zwarty, więc można z niego wybrać
podpokrycie skończone, powiedzmy
.
Oczywiście jest to także pokrycie zbioru .
Jeśli wśród zbiorów
znajduje się zbiór to można go
usunąć (gdyż ) i nadal będzie to skończone
pokrycie zbioru będące podpokryciem pokrycia
.
Pokazaliśmy zatem, że zbiór jest zwarty.
(5) Niech będzie zbiorem zwartym oraz
zbiorem domkniętym.
Z (1) wiemy, że jest także domknięty,
zatem jest zbiorem domkniętym
(patrz twierdzenie 1.10. (9)).
Ponieważ jest domkniętym podzbiorem zbioru zwartego
, więc z (3) wiemy, że jest on zbiorem zwartym,
co należało dowieść.
(1) Z twierdzenia 1.19. wynika w szczególności, że dowolny zbiór zwarty w przestrzeni metrycznej jest domknięty i ograniczony.
Implikacja odwrotna nie
jest prawdziwa.
Jako przykład weźmy zbiór nieskończony z metryką dyskretną.
Cały zbiór jest domknięty
(jako uzupełnienie zbioru otwartego ) oraz
ograniczony (ponieważ patrz przykład 1.13.).
Ale nie jest to zbiór zwarty, ponieważ z pokrycia otwartego
nie można wybrać pokrycia skończonego
(zauważmy, że
i usunięcie jakiegokolwiek zbioru z rodziny zbiorów otwartych
powoduje, że rodzina ta przestaje być pokryciem
).
(2)
Okazuje się jednak, że w
przestrzeni euklidesowej twierdzenie odwrotne jest
prawdziwe. Twierdzenie to bez dowodu poznaliśmy i
wykorzystywaliśmy na wykładzie z Analizy Matematycznej 1,
udowodnimy go na następnym wykładzie
(patrz wniosek 2.26.).
Poniższe twierdzenie daje pełną odpowiedź na pytanie, jakie przedziały w są zwarte.
Twierdzenie 1.21.
Przedział domknięty i ograniczony () jest zbiorem zwartym.
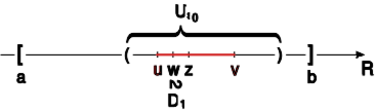
Dowód 1.21. [nadobowiązkowy]
Dowód oparty jest na tak zwanych przekrojach Dedekinda.
Niech będzie dowolnym pokryciem
przedziału (gdzie ).
Skonstruujemy dwa zbiory
(tak zwane przekroje Dedekinda)
w następujący sposób:
", wtedy i tylko wtedy, gdy
(1)
lub
(2) oraz przedział jest pokryty skończoną
liczbą zbiorów otwartych z rodziny ."
Natomiast:
", wtedy i tylko wtedy, gdy ."
Oczywiście
(bo przedział jest pokryty przez
jeden ze zbiorów pokrycia ).
Zdefiniujmy
. Oczywiście .
Pokażemy, że
.
Dla dowodu niewprost przypuśćmy, że
.
Z definicji pokrycia wiemy, że
Z definicji zbioru otwartego w metryce euklidesowej w wiemy, że
i
Z kolei z definicji liczby wynika, że
,
to znaczy przedział jest pokryty skończoną ilością zbiorów z pokrycia , powiedzmy
Wówczas
czyli , ale to jest sprzeczne z definicją . Zatem wykazaliśmy, że .
Teraz w analogiczny sposób jak wyżej pokazujemy, że , skąd wynika teza naszego twierdzenia.
Twierdzenie 1.22.
Przedziały otwarte i otwarto-domknięte nie są zwarte w .
Dowód 1.22.
Aby pokazać, że przedziały otwarte i otwarto-domknięte nie są zwarte, wskażemy pokrycia otwarte tych przedziałów, z których nie można wybrać podpokryć skończonych. Niech .
Uzasadnienie, iż z powyższych pokryć nie można wybrać pokryć skończonych, pozostawiamy jako proste ćwiczenie.
Spójność
Ostatnim pojęciem, jakie wprowadzimy na tym wykładzie, jest spójność zbioru w przestrzeni metrycznej. Intuicyjnie spójność zbioru oznacza, że składa się on z "jednego kawałka". Jednak, aby formalnie zdefiniować to pojęcie potrzebujemy nieco bardziej skomplikowanej definicji.
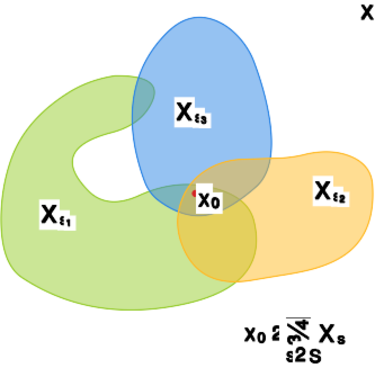
Definicja 1.23. [zbiór spójny]
Niech będzie przestrzenią metryczną
.
Zbiór nazywamy spójnym,
jeśli nie jest zawarty w sumie dwóch zbiorów otwartych,
rozłącznych, z którymi ma niepuste przecięcie,
to znaczy nie istnieją dwa zbiory i takie, że
Przykład 1.24.
Pierwszy z poniższych rysunków przedstawia zbiór spójny .
Jeśli dwa zbiory i są otwarte, rozłączne i mają niepuste
przecięcie z , to nie mogą w sumie zawierać całego
(to znaczy ).
Zbiór na kolejnym rysunku nie jest spójny,
gdyż istnieją dwa zbiory i spełniające wszystkie cztery
warunki z definicji spójności zbioru.
Twierdzenie 1.25.
Jeśli , to jest zbiorem spójnym wtedy i tylko wtedy, gdy jest przedziałem.
Dowód 1.25. [nadobowiązkowy]
[Szkic]
""
Niech będzie zbiorem spójnym.
Dla dowodu niewprost przypuśćmy, że nie jest przedziałem,
to znaczy
Zdefiniujmy
Wówczas i są zbiorami otwartymi (dlaczego?),
i
(bo i ),
oraz .
Jest to sprzeczne ze spójnością zbioru .
"" (Będziemy korzystali z faktu, że supremum zbioru otwartego
w nie jest elementem tego zbioru).
Niech będzie przedziałem.
Dla dowodu niewprost przypuśćmy, że nie jest zbiorem
spójnym.
Zatem istnieją dwa niepuste zbiory otwarte i
takie, że
oraz
Bez straty ogólności możemy założyć, że
.
Zdefiniujmy .
Ponieważ i jest otwarty, więc .
Gdyby , to z faktu, że jest zbiorem otwartym
wynikałoby, że nie jest kresem górnym zbioru .
Zatem .
Ponieważ i jest otwarty, więc .
Gdyby , to z faktu, że jest otwarty wynikałoby, że
nie jest kresem górnym zbioru .
Zatem .
Pokazaliśmy, że . Ale ,
więc doszliśmy do sprzeczności z faktem, że
.
Pokazaliśmy zatem, że
jest zbiorem spójnym.
Kolejne twierdzenie (które podajemy bez dowodu) mówi, że suma dowolnej rodziny zbiorów spójnych jest zbiorem spójnym, pod warunkiem, że mają one niepuste przecięcie.
Twierdzenie 1.26.
Jeśli jest przestrzenią metryczną, jest rodziną podzbiorów spójnych w takich, że , to zbiór jest spójny.