Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne

Przestrzenie metryczne

Ten wykład poświęcony jest pojęciu przestrzeni metrycznej. Prezentujemy definicję metryki i przykłady przestrzeni metrycznych. Definiujemy zbiory otwarte, domknięte, punkty skupienia i średnicę zbioru. Następnie wprowadzamy pojęcia zwartości i spójności w przestrzeniach metrycznych. Dowodzimy, że przedział domknięty i ograniczony jest zbiorem zwartym w $\mathbb{ℝ}$ oraz charakteryzujemy zbiory spójne w $\mathbb{ℝ}$.

Jedną z najistotniejszych idei matematyki jest idea aproksymacji. Z aproksymacją mamy do czynienia wtedy, gdy pewien obiekt $T$ (liczbę, funkcję, zbiór) przedstawiamy jako granicę (w odpowiednim sensie) ciągu obiektów $T_n$. Możemy wtedy wnioskować o własnościach "mniej znanego" obiektu $T$ z własności "bardziej znanych" obiektów $T_n$. Każdy z nas zetknął się z aproksymacją, chociażby w stwierdzeniu "$\pi$ wynosi mniej więcej $3.14$" (tu przybliżamy liczbę niewymierną ciągiem liczb wymiernych). Na wykładzie poświęconym ciągom funkcyjnym dowiemy się, że jeśli funkcja jest granicą (w specjalnym sensie) ciągu funkcji ciągłych to jest funkcją ciągłą. Ponieważ mamy wiele różnych rodzajów zbieżności (czyli przejść granicznych) potrzebna jest w matematyce w miarę ogólna, a zarazem prosta teoria przechodzenia do granicy. O podstawach tej teorii opowiemy na dwóch pierwszych wykładach poświęconych przestrzeniom metrycznym i ciągom w przestrzeniach metrycznych. Na trzecim wykładzie zajmiemy się działem teorii przestrzeni metrycznych - przestrzeniami unormowanymi. Teoria ta pozwala dodatkowo "przenieść" do teorii granic ważne idee geometryczne związane z działaniami na wektorach.

Metryka

Przypomnijmy, że różne sposoby mierzenia odległości w ${\mathbb{ℝ}}^N$ poznaliśmy na wykładzie z Analizy matematycznej 1. Tam też zapoznaliśmy się z pojęciem metryki. Okazuje się, że funkcję zwaną metryką można zdefiniować dla dowolnego (niepustego) zbioru $X$ (a nie tylko dla ${\mathbb{ℝ}}^N$). W ten sposób będziemy mogli mierzyć odległości między elementami dowolnego zbioru $X$.

Definicja 1.1. [metryka, odległość]

Niech $X$ będzie zbiorem niepustym. Metryką w zbiorze $X$ nazywamy dowolną funkcję $d:X\times X⟶{\mathbb{ℝ}}_{+}=[0,+\mathrm{\infty })$ spełniającą następujące warunki:
(i) $\mathrm{\forall }x\in X:d(x,y)=0⟺x=y$;
(ii) $\mathrm{\forall }x,y\in X:d(x,y)=d(y,x)$ (warunek symetrii);
(iii) $\mathrm{\forall }x,y,z\in X:d(x,y)+d(y,z)\ge d(x,z)$ (warunek trójkąta).
Parę $(X,d)$ nazywamy przestrzenią metryczną.
Dla dowolnych $x,y\in X,$ liczbę $d(x,y)$ nazywamy odległością punktów $x$ i $y$ oraz mówimy, że punkty $x$ i $y$ są oddalone od siebie o $d(x,y)$.

Definicja kuli w dowolnej przestrzeni metrycznej jest analogiczna do poznanej na wykładzie z Analizy Matematycznej 1 definicji kuli w ${\mathbb{ℝ}}^N$.

Definicja 1.2. [kula, kula domknięta]

Niech $(X,d)$ będzie przestrzenią metryczną. Kulą o środku w punkcie $x_0\in X$ i promieniu $r\ge 0$ nazywamy zbiór:

$K(x_0,r)\stackrel{df}{=}\{x\in X:d(x_0,x)<r\}.$

Kulą domkniętą o środku w punkcie $x_0\in X$ i promieniu $r\ge 0$ nazywamy zbiór:

$\bar{K}(x_0,r)\stackrel{df}{=}\{x\in X:d(x_0,x)\le r\}.$

Podamy teraz kilka przykładów przestrzeni metrycznych oraz opiszemy, jak wyglądają kule w tych przestrzeniach.

Metryka dyskretna

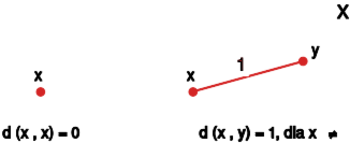
Przykład 1.3. [Metryka dyskretna]

Niech $X\ne \mathrm{\varnothing }$ będzie dowolnym zbiorem oraz niech

$d_d(x,y)\stackrel{df}{=}\{\begin{array}{lll}1& \text{gdy}& x\ne y,\\ 0& \text{gdy}& x=y.\end{array}\mathrm{\forall }x,y\in X.$

Zauważmy, iż wartość funkcji $d$ dla dwóch dowolnych punktów wynosi $1,$ gdy są one różne oraz wynosi $0,$ gdy jest to ten sam punkt.

Łatwo sprawdzić, że tak zdefiniowana funkcja $d$ jest metryką, zatem para $(X,d_d)$ jest przestrzenią metryczną. Metrykę tę będziemy nazywali metryczną dyskretną. Faktycznie, z definicji wynika, że dla dowolnych $x,y\in X$ mamy

$d_d(x,y)=0⟺x=y$

oraz

$d_d(x,y)=d_d(y,x).$

Dla sprawdzenia warunku trójkąta weźmy $x,y,z\in X$. Rozważymy następujące przypadki.

1) Jeśli $x=z,$ to $d(x,z)=0$ zatem zawsze zachodzi $d_d(x,z)=0\le d_d(x,y)+d_d(y,z)$.

2) Jeśli $x\ne z,$ to $x\ne y$ lub $y\ne z$. Wtedy również $d_d(x,z)=1\le d_d(x,y)+d_d(y,z)$.

Łatwo także zauważyć, jak będą wyglądały kule w tej przestrzeni metrycznej. Jeśli $r\in (0,1],$ to kula o promieniu $r$ składa się z samego środka, ale jeśli $r>1,$ to kulą jest cała przestrzeń $X$. Mamy zatem

$K(x_0,r)=\{\begin{array}{lll}\mathrm{\varnothing }& \text{gdy}& r=0,\\ \{x_0\}& \text{gdy}& r\in (0,1],\\ X& \text{gdy}& r>1,\end{array}$

$\bar{K}(x_0,r)=\{\begin{array}{lll}\{x_0\}& \text{gdy}& r\in [0,1),\\ X& \text{gdy}& r\ge 1.\end{array}$

Zatem w przestrzeni metrycznej dyskretnej kulami i kulami domkniętymi są jedynie:

$\mathrm{\varnothing },$ zbiory jednopunktowe oraz cała przestrzeń.

Przypomnijmy teraz standardowe metryki w ${\mathbb{ℝ}}^N$. Były one wprowadzone na wykładzie z Analizy Matematycznej 1.

Euklides (365-300 p.n.e.)
Zobacz biografię

Przykład 1.4. [Metryka maksimowa, taksówkowa i euklidesowa]

Niech $X={\mathbb{ℝ}}^N$ oraz niech

$\mathrm{\forall }x,y\in {\mathbb{ℝ}}^N:quad{d}_{\mathrm{\infty }}(x,y)\stackrel{df}{=}\underset{i=1,\dots ,N}{\max }|x_i-y_i|,$
$d_1(x,y)\stackrel{df}{=}\sum _{i=1}^N|x_i-y_i|,$

$d_2(x,y)\stackrel{df}{=}\sqrt{\sum _{i=1}^N{(x_i-y_i)}^2},$

gdzie $x=(x_1,\dots ,x_N)$ oraz $y=(y_1,\dots ,y_N)$.
Para $({\mathbb{ℝ}}^N,d_{\mathrm{\infty }})$ jest przestrzenią metryczną. Funkcję $d_{\mathrm{\infty }}$ nazywamy metryką maksimową w ${\mathbb{ℝ}}^N$.
Para $({\mathbb{ℝ}}^N,d_1)$ jest przestrzenią metryczną. Funkcję $d_1$ nazywamy metryką taksówkową w ${\mathbb{ℝ}}^N$.
Para $({\mathbb{ℝ}}^N,d_2)$ jest przestrzenią metryczną. Funkcję $d_2$ nazywamy metryką euklidesową w ${\mathbb{ℝ}}^N,$ zaś parę $({\mathbb{ℝ}}^N,d_2)$ nazywamy przestrzenią metryczną euklidesową.

Przypomnijmy, jak wyglądają kule w tych metrykach.

Plik:AM1.M03.W.R05.svg Kula w metryce maksimowej w ${\mathbb{ℝ}}^2$

Plik:AM1.M03.W.R06.svg Kula w metryce maksimowej w ${\mathbb{ℝ}}^3$

Plik:AM1.M03.W.R09.svg Kula w metryce taksówkowej w ${\mathbb{ℝ}}^2$

Plik:AM1.M03.W.R10.svg Kula w metryce taksówkowej w ${\mathbb{ℝ}}^3$

Plik:AM1.M03.W.R14.svg Kula w metryce euklidesowej w ${\mathbb{ℝ}}^2$

Plik:AM1.M03.W.R15.svg Kula w metryce euklidesowej w ${\mathbb{ℝ}}^3$

Dwa kolejne przykłady podają mniej typowe metryki na płaszczyźnie ${\mathbb{ℝ}}^2$.

Plik:AM2.M01.W.R02.svg Metryka rzeka

Plik:AM2.M01.W.R03.svg Metryka rzeka

Plik:AM2.M01.W.R05.svg

Metryka kolejowa

Przykład 1.5. [Metryka rzeka]

Wyobraźmy sobie, że płaszczyzna ${\mathbb{ℝ}}^2$ jest gęstym lasem oraz pewna prosta $l$ jest rzeką. Aby zmierzyć odległość dwóch punktów $x,y\in {\mathbb{ℝ}}^2$, musimy wyciąć ścieżkę od $x$ do $y,$ przy czym możemy to robić tylko prostopadle do rzeki.

Mamy dwa przypadki:

(1) Jeśli punkty $x$ i $y$ są końcami odcinka prostopadłego do rzeki $l,$ to ich odległość jest równa zwykłej odległości euklidesowej na płaszczyźnie.

(2) Jeśli zaś punkty $x$ i $y$ nie leżą na prostej prostopadłej do rzeki $l,$ to musimy utworzyć dwie ścieżki jedną od punktu $x$ do rzeki, a drugą od rzeki do punktu $y,$ zawsze prostopadle do rzeki. Teraz odległość od $x$ do $y$ będzie równa długości (euklidesowej) obu ścieżek oraz odległości tych ścieżek na rzece.
Nietrudno sprawdzić, że tak utworzona funkcja $d$ jest metryką w ${\mathbb{ℝ}}^2$.

Nazywamy ją metryką rzeką.

Przykład 1.6. [Metryka kolejowa]

Wyobraźmy sobie, że na płaszczyźnie wyróżniony jest jeden punkt $O,$ węzeł kolejowy, od którego odchodzą półproste, szyny, we wszystkich kierunkach. Aby zmierzyć odległość miedzy dwoma punktami $x$ i $y$, musimy przebyć drogę między nimi, poruszając się po szynach. Rozważmy dwa przypadki:
(1) Jeśli punkty $x$ i $y$ znajdują się na wspólnej półprostej wychodzącej z punktu $O,$ to ich odległość jest zwykłą odległością euklidesową.
(2) Jeśli zaś punkty $x$ i $y$ nie leżą na wspólnej półprostej wychodzącej z punktu $O$ to ich odległość jest równa sumie odległości euklidesowych od $x$ do $O$ oraz od $O$ do $y$.
Tak wprowadzona funkcja odległości jest metryką,

zwaną metryką kolejową.

Plik:AM2.M01.W.R04.mp4 | Plik:.mp4 AM2.M01.W.R04

Plik:AM2.M01.W.R06.mp4 | Plik:.mp4 Kule w metryce kolejowej

Zdefiniujemy teraz pewne pojęcia związane z przestrzeniami metrycznymi. Część z nich była zdefiniowana na Analizie Matematycznej 1.

Plik:AM1.M03.W.R16.svg

Zbiór otwarty

Definicja 1.7.

Niech $(X,d)$ będzie przestrzenią metryczną, niech $x_0\in X$ oraz $A\subseteq X$.
(1) Zbiór $U\subseteq X$ nazywamy otwartym, jeśli każdy punkt zbioru $U$ zawiera się w $U$ wraz z pewną kulą, czyli

$\mathrm{\forall }x\in U\mathrm{\exists }r>0:K(x,r)\subseteq U.$

(2) Punkt $x_0$ nazywamy punktem wewnętrznym zbioru $A\subseteq X,$ jeśli istnieje kula o środku w punkcie $x_0$ (i dodatnim promieniu) taka, że zawiera się w $A$. Wnętrzem zbioru $A$ nazywamy zbiór jego punktów wewnętrznych i oznaczamy go $\mathrm{i}\mathrm{n}\mathrm{t}A$.
(3) Domknięciem zbioru $A\subseteq X$ nazywamy zbiór wszystkich punktów $A$ oraz wszystkich punktów skupienia zbioru $A$ i oznaczamy go $\bar{A}$.
(4) Brzegiem zbioru $A$ nazywamy zbiór $\partial A:=\bar{A}\setminus \mathrm{i}\mathrm{n}\mathrm{t}A$.

Przykład 1.8.

W przestrzeni metrycznej dyskretnej każdy zbiór jest otwarty, bo wraz z każdym punktem $x$ zawiera kulę $K(x,1)=\{x\}$.

Przykład 1.9.

W przestrzeni ${\mathbb{ℝ}}^2$ z metryką euklidesową rozważmy zbiór $A=\{(x_1,x_2):2<x_1^2+x_2^2\le 4\}$. Wówczas

$\begin{array}{rl}\mathrm{i}\mathrm{n}\mathrm{t}A& =\{(x_1,x_2):2<x_1^2+x_2^2<4\},\\ \bar{A}& =\{(x_1,x_2):2\le x_1^2+x_2^2\le 4\},\\ \partial A& =\{(x_1,x_2):x_1^2+x_2^2=2\}\cup \{(x_1,x_2):x_1^2+x_2^2=4\}.\end{array}$

Podobnie jak w ${\mathbb{ℝ}}^N$ tak i w dowolnej przestrzeni metrycznej zachodzą następujące własności.

Twierdzenie 1.10. [Zbiory w przestrzeniach metrycznych]

Jeśli $(X,d)$ jest przestrzenią metryczną, to
(1) Każda kula jest zbiorem otwartym w $X$.
(2) Zbiór $U\subseteq X$ jest otwarty, wtedy i tylko wtedy, gdy $U^c$ (dopełnienie zbioru $U$) jest zbiorem domkniętym.
(3) Kula domknięta jest zbiorem domkniętym.
(4) Jeśli $x_0$ jest punktem skupienia zbioru $A\subseteq X,$ to dowolna kula o środku w punkcie $x_0$ (i dodatnim promieniu) zawiera nieskończenie wiele punktów zbioru $A$.
(5) Suma dowolnej rodziny zbiorów otwartych jest zbiorem otwartym.
(6) Przecięcie (część wspólna) skończonej rodziny zbiorów otwartych jest zbiorem otwartym.
(7) Przecięcie (część wspólna) dowolnej rodziny zbiorów domkniętych jest zbiorem domkniętym.
(8) Suma skończonej rodziny zbiorów domkniętych jest zbiorem domkniętym.
(9) Dla dowolnego zbioru $A\subseteq X,$ zbiór $\bar{A}$ (domknięcie zbioru $A$) jest zbiorem domkniętym.

Omówienie i przykłady powyższych własności mieliśmy na wykładzie z Analizy Matematycznej 1 (patrz Analiza matematyczna 1 przykład 3.15.).

Kolejne pojęcia związane z przestrzeniami metrycznymi podane są w poniższej definicji.

Definicja 1.11.

(1) Srednicą zbioru $A$ nazywamy liczbę:

$\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}A\stackrel{df}{=}\underset{x,y\in A}{\sup }d(x,y);$

(2) Odległością punktu $x_0$ od zbioru $A$ nazywamy liczbę:

$\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}(x_0,A)\stackrel{df}{=}\underset{x\in A}{\inf }d(x_0,x).$

(3) Mówimy, że zbiór $A\subseteq X$ jest ograniczony, jeśli jest zawarty w pewnej kuli, to znaczy

$\mathrm{\exists }r>0\mathrm{\exists }{x}_0\in X:A\subseteq K(x_0,r).$

Plik:AM1.M03.C.R01.mp4 | Plik:.mp4 Odległość punktu od zbioru

Plik:AM2.M01.W.R07.mp4 | Plik:.mp4 Średnica zbioru

[[File:AM1.M03.W.R17.svg|253x Plik:.mp4 Zbiór ograniczony

Średnica zbioru i odległość punktu od zbioru

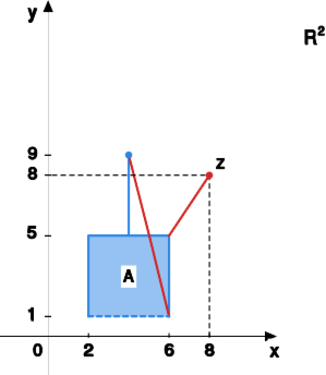
Przykład 1.12.

Na płaszczyźnie ${\mathbb{ℝ}}^2$ z metryką euklidesową rozważmy zbiór

$A=\{(x,y):2\le x\le 6,1<y\le 5\}\cup (\{4\}\times [5,9])$

oraz punkt $z=(8,8)$. Wyznaczyć średnicę zbioru $A$ oraz odległość punktu $z$ od zbioru $A$.

Z poniższego rysunku widzimy, że $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}A=\sqrt{2^2+8^2}=\sqrt{68}=2\sqrt{17}$

oraz $\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}(z,A)=\sqrt{2^2+3^2}=\sqrt{13}$.

Przykład 1.13.

Niech $(X,d_d)$ będzie przestrzenią metryczną dyskretną. Jeśli $\mathrm{\#}X\le 1,$ to $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}X=0,$ a jeśli $\mathrm{\#}X\ge 2,$ to $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}X=1$. Zatem każdy zbiór w metryce dyskretnej jest ograniczony.

Następujące oczywiste twierdzenie podaje związek między ograniczonością zbioru oraz jego średnicą.

Twierdzenie 1.14.

Jeśli $(X,d)$ jest przestrzenią metryczną, $A\subseteq X,$ to zbiór $A$ jest ograniczony wtedy i tylko wtedy, gdy $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}A<+\mathrm{\infty }$.

W iloczynie kartezjańskim przestrzeni metrycznych można także zadać metrykę (tak zwaną metrykę produktową) na kilka naturalnych sposobów. Poniższe twierdzenie podaje jeden z takich sposobów. [[grafika:Kartezjusz.jpg|thumb|right||Kartezjusz (1596-1650)
Zobacz biografię]]

Twierdzenie 1.15. [Iloczyn kartezjański przestrzeni metrycznych]

Jeśli $(X_i,d_i)$ są przestrzeniami metrycznymi dla $i=1,\dots ,k,X\stackrel{df}{=}{X}_1\times \dots \times X_k,d:X\times X⟶{\mathbb{ℝ}}_{+}$ jest funkcją zdefiniowaną przez

$d(x,y)\stackrel{df}{=}\sqrt{\sum _{i=1}^k{d}_i(x_i,y_i{)}^2}\mathrm{\forall }x,y\in X,$

to $(X,d)$ jest przestrzenią metryczną.
Wówczas $d$ nazywamy metryką produktową lub metryką standardową w iloczynie kartezjańskim $X_1\times \dots \times X_k$.

Dowód 1.15.

Dowód oparty na nierówności Cauchy'ego (patrz Analiza matematyczna 1 lemat 3.8.) jest analogiczny do dowodu, że $d_2$ jest metryką w ${\mathbb{ℝ}}^N$ (porównaj Analiza matematyczna 1 przykład 3.7. i lemat 3.9.).

Uwaga 1.16.

Metryka euklidesowa w ${\mathbb{ℝ}}^N$ jest metryką standardową w ${\mathbb{ℝ}}^N=\underset{N}{\underbrace{\mathbb{ℝ}\times \dots \times \mathbb{ℝ}}}$. Wynika to wprost z definicji obu metryk.

Uwaga 1.17.

Jeśli $(X,d)$ jest przestrzenią metryczną oraz $A\subseteq X,$ to zbiór $A$ jest także przestrzenią metryczną z metryką $d{|}_{A\times A}$. Kule w przestrzeni $A$ są równe przecięciom kul z przestrzeni $X$ ze zbiorem $A$. Metrykę na $A$ nazywamy metryką indukowaną. W przyszłości o podzbiorach przestrzeni metrycznej będziemy także mówili "przestrzeń metryczna".

Zwartość

Wprowadzimy teraz ogólniejsze pojęcie zwartości niż to, z którym spotkaliśmy się na wykładzie z Analizy Matematycznej 1 (patrz Analiza matematyczna 1 definicja 8.21.).

Load video

Local File

Local File might collect personal data.

Continue Dismiss

Pokrycie zbioru

Definicja 1.18.

Niech $(X,d)$ będzie przestrzenią metryczną oraz $A\subseteq X:$
(1) Pokryciem otwartym zbioru $A$ nazywamy dowolną rodzinę $\{U_s{\}}_{s\in S}\subseteq 2^X$ zbiorów otwartych taką, że $\bigcup _{s\in S}{U}_s\supseteq A$.
Pokrycie to nazywamy skończonym, jeśli $\mathrm{\#}S<+\mathrm{\infty }$.
(2) Mówimy, że $\{U_s{\}}_{s\in T}$ jest podpokryciem pokrycia $\{U_s{\}}_{s\in S}$ zbioru $A,$ jeśli $\{U_s{\}}_{s\in T}$ jest pokryciem zbioru $A$ oraz $T\subset S$.
(3) Mówimy, że zbiór $A$ jest zwarty, jeśli z każdego pokrycia otwartego zbioru $A$ można wybrać pokrycie skończone.

Kolejne twierdzenie zbiera pewne informacje dotyczące zbiorów zwartych w przestrzeniach metrycznych.

Twierdzenie 1.19.

W dowolnej przestrzeni metrycznej $X$ mamy
(1) Zbiór skończony jest zwarty.
(2) Podzbiór zwarty przestrzeni metrycznej jest domknięty.
(3) Podzbiór zwarty przestrzeni metrycznej jest ograniczony.
(4) Podzbiór domknięty zbioru zwartego jest zwarty.
(5) Część wspólna zbioru zwartego i domkniętego jest zbiorem zwartym.

Dowód 1.19. [nadobowiązkowy]

(Ad (1)) Niech $A=\{a_1,\dots ,a_k\}$ będzie zbiorem skończonym w $X$ i niech $\{U_s{\}}_{s\in S}$ będzie pokryciem otwartym zbioru $A$. Z definicji pokrycia mamy w szczególności

$\mathrm{\forall }i\in \{1,\dots ,k\}\mathrm{\exists }{s}_i\in S:a_i\in U_{s_i}.$

Zatem $A\subseteq \bigcup _{i=1}^k{U}_{s_i}$. Pokazaliśmy zatem, że $\{U_{s_i}{\}}_{i=1}^k$ jest podpokryciem (skończonym) pokrycia $\{U_s{\}}_{s\in S}$ zbioru $A$.
(Ad (2)) Niech $A$ będzie zwartym podzbiorem w $X$. Wystarczy pokazać, że $A^c$ jest zbiorem otwartym (patrz twierdzenie 1.10. (6)). W tym celu niech $x\in A^c$. Dla dowolnego $y\in A$ niech $0<r_y<\frac{1}{2}d(x,y)$. Wówczas $x\in ̸K(y,r_y)$ oraz $K(y,r_y)\cap K(x,r_y)=\mathrm{\varnothing }$.
Rodzina $\{K(y,r_y){\}}_{y\in A}$ jest pokryciem otwartym zbioru $A$. Ponieważ $A$ jest zbiorem zwartym, więc możemy z tego pokrycia wybrać podpokrycie skończone, powiedzmy $\{K(y_i,r_{y_i}){\}}_{i=1}^k,$ zatem

$W\stackrel{df}{=}K(y_1,r_{y_1})\cup \dots \cup K(y_k,r_{y_k})\supseteq A.$

Niech $V\stackrel{df}{=}\bigcap _{i=1}^{k}K(x,r_{y_k})$. Wówczas $V$ jest kulą o środku w punkcie $x$ taką, że $V\subseteq A^c,$ czyli $x$ jest punktem wewnętrznym zbioru $A^c$. Pokazaliśmy więc, że zbiór $A^c$ jest otwarty, a zatem zbiór $A$ jest domknięty.
(Ad (3)) Niech $A$ będzie zwartym podzbiorem w $X$. Należy pokazać, że zbiór $A$ jest ograniczony. Niech $x_0\in X$ będzie dowolnym punktem. Zauważmy, że

$A\subseteq X=\bigcup _{n=1}^{\mathrm{\infty }}K(x_0,n),$

to znaczy rodzina kul $\{K(x_n,n){\}}_{n\in \mathbb{\mathbb{N}}}$ jest pokryciem otwartym zbioru $A$. Z zwartości zbioru $A$ wynika, iż z tego pokrycia można wybrać podpokrycie skończone, to znaczy

$\mathrm{\exists }k\in \mathbb{\mathbb{N}}:A\subseteq \bigcup _{n=1}^{k}K(x_0,n).$

Ale ciąg kul $\{K(x_0,n){\}}_{n\in \mathbb{\mathbb{N}}}$ jest wstępujący, a więc

$A\subseteq \bigcup _{n=1}^{k}K(x_0,n)=K(x_0,k),$

zatem zbiór $A$ jest ograniczony.
(Ad (4)) Niech $A$ będzie domkniętym podzbiorem zbioru zwartego $B$. Niech $\{U_s{\}}_{s\in S}$ będzie dowolnym pokryciem zbioru $A$. Ponieważ $A$ jest domknięty, więc $A^c=X\setminus A$ jest zbiorem otwartym (patrz twierdzenie 1.10. (6)). Niech $t\in ̸S,$ będzie nowym indeksem oraz zdefiniujmy $U_t=A^c$. Niech $T=S\cup \{t\}$. Wówczas

$U_t\cup \bigcup _{s\in S}{U}_s=\bigcup _{s\in T}{U}_s=X\supseteq B,$

zatem $\{U_s{\}}_{s\in T}$ jest pokryciem zbioru $B$. Ponieważ zbiór $B$ jest zwarty, więc można z niego wybrać podpokrycie skończone, powiedzmy $U_{s_1},\dots ,U_{s_k}$. Oczywiście jest to także pokrycie zbioru $A$. Jeśli wśród zbiorów $U_{s_1},\dots ,U_{s_k}$ znajduje się zbiór $U_t$ to można go usunąć (gdyż $U_t\cap A=\mathrm{\varnothing }$) i nadal będzie to skończone pokrycie zbioru $A$ będące podpokryciem pokrycia $\{U_s{\}}_{s\in S}$. Pokazaliśmy zatem, że zbiór $A$ jest zwarty.
(5) Niech $A$ będzie zbiorem zwartym oraz $B$ zbiorem domkniętym. Z (1) wiemy, że $A$ jest także domknięty, zatem $A\cap B$ jest zbiorem domkniętym (patrz twierdzenie 1.10. (9)). Ponieważ $A\cap B$ jest domkniętym podzbiorem zbioru zwartego $A,$ więc z (3) wiemy, że jest on zbiorem zwartym, co należało dowieść.

Load video Local File Local File might collect personal data. Continue Dismiss | Plik:.mp4 Rysunek do dowodu twierdzenia 1.19

Load video Local File Local File might collect personal data. Continue Dismiss | Plik:.mp4 Rysunek do dowodu twierdzenia 1.19

Uwaga 1.20.

(1) Z twierdzenia 1.19. wynika w szczególności, że dowolny zbiór zwarty w przestrzeni metrycznej jest domknięty i ograniczony.

Implikacja odwrotna nie jest prawdziwa. Jako przykład weźmy zbiór nieskończony $X$ z metryką dyskretną. Cały zbiór $X$ jest domknięty (jako uzupełnienie zbioru otwartego $\mathrm{\varnothing }$) oraz ograniczony (ponieważ $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}X=1;$ patrz przykład 1.13.). Ale nie jest to zbiór zwarty, ponieważ z pokrycia otwartego $\bigcup _{x\in X}K(x,\frac{1}{2})\supseteq X$ nie można wybrać pokrycia skończonego (zauważmy, że $K(x,\frac{1}{2})=\{x\}$ i usunięcie jakiegokolwiek zbioru z rodziny zbiorów otwartych $\left\{K\right(x,\frac{1}{2}){\}}_{x\in X}$ powoduje, że rodzina ta przestaje być pokryciem $X$).
(2) Okazuje się jednak, że w przestrzeni euklidesowej ${\mathbb{ℝ}}^N$ twierdzenie odwrotne jest prawdziwe. Twierdzenie to bez dowodu poznaliśmy i wykorzystywaliśmy na wykładzie z Analizy Matematycznej 1, udowodnimy go na następnym wykładzie (patrz wniosek 2.26.).

Poniższe twierdzenie daje pełną odpowiedź na pytanie, jakie przedziały w $\mathbb{ℝ}$ są zwarte.

Twierdzenie 1.21.

Przedział domknięty i ograniczony $[a,b]\subseteq \mathbb{ℝ}$ ($-\mathrm{\infty }<a<b<\mathrm{\infty }$) jest zbiorem zwartym.

Rysunek do dowodu twierdzenia 1.21

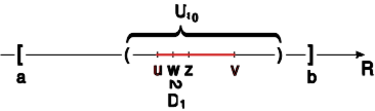
Dowód 1.21. [nadobowiązkowy]

Dowód oparty jest na tak zwanych przekrojach Dedekinda.
Niech $\{U_s{\}}_{s\in S}$ będzie dowolnym pokryciem przedziału $P=[a,b]$ (gdzie $a<b$). Skonstruujemy dwa zbiory $D_1,D_2\subseteq \mathbb{ℝ}$ (tak zwane przekroje Dedekinda) w następujący sposób:
"$x\in D_1$, wtedy i tylko wtedy, gdy
(1) $x<a$ lub
(2) $a\le x<b$ oraz przedział $[a,x]$ jest pokryty skończoną liczbą zbiorów otwartych z rodziny $\{U_s{\}}_{s\in S}$."
Natomiast:
"$x\in D_2$, wtedy i tylko wtedy, gdy $x\in ̸D_1$."
Oczywiście $a\in D_1$ (bo przedział $[a,a]=\{a\}$ jest pokryty przez jeden ze zbiorów pokrycia $\{U_s{\}}_{s\in S}$).
Zdefiniujmy $z\stackrel{df}{=}\sup D_1$. Oczywiście $z\in [a,b]$.
Pokażemy, że $z=b$. Dla dowodu niewprost przypuśćmy, że $z<b$. Z definicji pokrycia wiemy, że

$\mathrm{\exists }{s}_0\in S:z\in U_{s_0}.$

Z definicji zbioru otwartego w metryce euklidesowej w $\mathbb{ℝ}$ wiemy, że

$\mathrm{\exists }u,v:u<z<v$ i $[u,v]\subseteq U_{s_0}.$

Z kolei z definicji liczby $z$ wynika, że

$\mathrm{\exists }w\in (u,z):w\in D_1,$

to znaczy przedział $[a,w]$ jest pokryty skończoną ilością zbiorów z pokrycia $\{U_s{\}}_{s\in S},$ powiedzmy

$[a,w]\subseteq U_{s_1}\cup U_{s_2}\cup \dots \cup U_{s_k}.$

Wówczas

$[a,v]\subseteq U_{s_1}\cup U_{s_2}\cup \dots \cup U_{s_k}\cup U_{s_0},$

czyli $v\in D_1,$ ale to jest sprzeczne z definicją $z$. Zatem wykazaliśmy, że $z=b$.

Teraz w analogiczny sposób jak wyżej pokazujemy, że $z\in D_1,$ skąd wynika teza naszego twierdzenia.

Twierdzenie 1.22.

Przedziały otwarte i otwarto-domknięte nie są zwarte w $\mathbb{ℝ}$.

Dowód 1.22.

Aby pokazać, że przedziały otwarte i otwarto-domknięte nie są zwarte, wskażemy pokrycia otwarte tych przedziałów, z których nie można wybrać podpokryć skończonych. Niech $a<b$.

$\begin{array}{rll}(a,b)& \subseteq & \bigcup _{n=1}^{\mathrm{\infty }}(a+\frac{1}{n},b+1),\\ (a,b]& \subseteq & \bigcup _{n=1}^{\mathrm{\infty }}(a+\frac{1}{n},b+1),\\ [a,b)& \subseteq & \bigcup _{n=1}^{\mathrm{\infty }}(a-1,b-\frac{1}{n})\\ (-\mathrm{\infty },b)& \subseteq & \bigcup _{n=1}^{\mathrm{\infty }}(-n,b),\\ (-\mathrm{\infty },b]& \subseteq & \bigcup _{n=1}^{\mathrm{\infty }}(-n,b+1),\\ (a,+\mathrm{\infty })& \subseteq & \bigcup _{n=1}^{\mathrm{\infty }}(a,n),\\ [a,+\mathrm{\infty })& \subseteq & \bigcup _{n=1}^{\mathrm{\infty }}(a-1,n)\\ (-\mathrm{\infty },+\mathrm{\infty })& \subseteq & \bigcup _{n=1}^{\mathrm{\infty }}(-n,n).\end{array}$

Uzasadnienie, iż z powyższych pokryć nie można wybrać pokryć skończonych, pozostawiamy jako proste ćwiczenie.

Spójność

Ostatnim pojęciem, jakie wprowadzimy na tym wykładzie, jest spójność zbioru w przestrzeni metrycznej. Intuicyjnie spójność zbioru $A$ oznacza, że składa się on z "jednego kawałka". Jednak, aby formalnie zdefiniować to pojęcie potrzebujemy nieco bardziej skomplikowanej definicji.

Definicja 1.23. [zbiór spójny]

Niech $(X,d)$ będzie przestrzenią metryczną $A\subseteq X$.
Zbiór $A$ nazywamy spójnym, jeśli nie jest zawarty w sumie dwóch zbiorów otwartych, rozłącznych, z którymi ma niepuste przecięcie, to znaczy nie istnieją dwa zbiory $U$ i $V$ takie, że

$\{\begin{array}{l}A\subseteq U\cup V\\ A\cap U\ne \mathrm{\varnothing },A\cap V\ne \mathrm{\varnothing }\\ U\cap V=\mathrm{\varnothing }\\ U,V\text{ - są otwarte. }\end{array}$

Przykład 1.24.

Pierwszy z poniższych rysunków przedstawia zbiór spójny $A$. Jeśli dwa zbiory $U$ i $V$ są otwarte, rozłączne i mają niepuste przecięcie z $A,$ to nie mogą w sumie zawierać całego $A$ (to znaczy $\mathrm{\exists }x\in A:x\in ̸U\cup V$).
Zbiór $B$ na kolejnym rysunku nie jest spójny, gdyż istnieją dwa zbiory $U$ i $V$ spełniające wszystkie cztery warunki z definicji spójności zbioru.

Plik:AM2.M01.W.R13.mp4 |253x Plik:.mp4 Zbiór spójny

Load video Local File Local File might collect personal data. Continue Dismiss |253x Plik:.mp4 Zbiór który nie jest spójny

Twierdzenie 1.25.

Jeśli $A\subseteq \mathbb{ℝ}$, to $A$ jest zbiorem spójnym wtedy i tylko wtedy, gdy $A$ jest przedziałem.

Suma zbiorów spójnych o niepustym przecięciu

Dowód 1.25. [nadobowiązkowy]

[Szkic]

"$⟹$"
Niech $A$ będzie zbiorem spójnym. Dla dowodu niewprost przypuśćmy, że $A$ nie jest przedziałem, to znaczy

$\mathrm{\exists }d\in A^c,\mathrm{\exists }a,b\in A:a<d<b.$

Zdefiniujmy

$U\stackrel{df}{=}(-\mathrm{\infty },d),V\stackrel{df}{=}(d,+\mathrm{\infty }).$

Wówczas $U$ i $V$ są zbiorami otwartymi (dlaczego?), $U\cap A\ne \mathrm{\varnothing }$ i $V\cap A\ne \mathrm{\varnothing }$ (bo $a\in U\cap A$ i $b\in V\cap A$), $A\subseteq U\cup V$ oraz $U\cap V=\mathrm{\varnothing }$. Jest to sprzeczne ze spójnością zbioru $A$.

"$⟸$" (Będziemy korzystali z faktu, że supremum zbioru otwartego w $\mathbb{ℝ}$ nie jest elementem tego zbioru).
Niech $A$ będzie przedziałem. Dla dowodu niewprost przypuśćmy, że $A$ nie jest zbiorem spójnym. Zatem istnieją dwa niepuste zbiory otwarte $U$ i $V$ takie, że

$U\cap V=\mathrm{\varnothing },A\subseteq U\cup V.$

oraz

$\mathrm{\exists }a,b\in A:a\in U,b\in V.$

Bez straty ogólności możemy założyć, że $a<b$.
Zdefiniujmy $z=\sup (U\cap [a,b])$. Ponieważ $b\in V$ i $V$ jest otwarty, więc $z<b$. Gdyby $z\in U,$ to z faktu, że $U$ jest zbiorem otwartym wynikałoby, że $z$ nie jest kresem górnym zbioru $U\cap [a,b]$. Zatem $z\in ̸U$.
Ponieważ $a\in U$ i $U$ jest otwarty, więc $a<z$. Gdyby $z\in V,$ to z faktu, że $V$ jest otwarty wynikałoby, że $z$ nie jest kresem górnym zbioru $U\cap [a,b]$. Zatem $z\in ̸V$.
Pokazaliśmy, że $z\in ̸U\cap V$. Ale $z\in A,$ więc doszliśmy do sprzeczności z faktem, że $A\subseteq U\cap V$.
Pokazaliśmy zatem, że $A$ jest zbiorem spójnym.

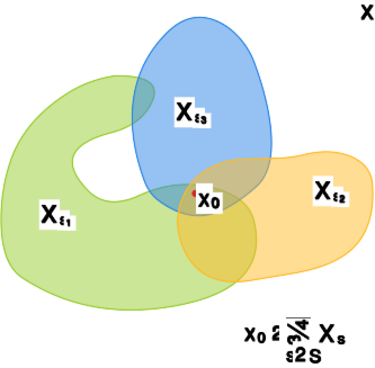
Kolejne twierdzenie (które podajemy bez dowodu) mówi, że suma dowolnej rodziny zbiorów spójnych jest zbiorem spójnym, pod warunkiem, że mają one niepuste przecięcie.

Twierdzenie 1.26.

Jeśli $(X,d)$ jest przestrzenią metryczną, $\{X_s{\}}_{s\in S}$ jest rodziną podzbiorów spójnych w $X$ takich, że $\bigcap _{s\in S}{X}_s\ne \mathrm{\varnothing },$ to zbiór $\bigcup _{s\in S}{X}_s$ jest spójny.