Analiza matematyczna 2/Ćwiczenia 3: Norma. Iloczyn skalarny: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „\displaystyle ” na „” |
m Zastępowanie tekstu – „\displaystyle” na „” |
||
| Linia 20: | Linia 20: | ||
Pokazać, że | Pokazać, że | ||
<math> | <math>\|\cdot\|_2,\|\cdot\|_1</math> oraz | ||
<math> | <math>\|\cdot\|_{\infty}</math> | ||
są normami | są normami | ||
(nazywamy je odpowiednio normą euklidesową, | (nazywamy je odpowiednio normą euklidesową, | ||
| Linia 29: | Linia 29: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' | '''(1)''' | ||
Pokazać, że <math> | Pokazać, że <math>\|\cdot\|_2</math> jest normą | ||
wprost z definicji normy. | wprost z definicji normy. | ||
Przy dowodzie subaddytywności wykorzystać nierówność | Przy dowodzie subaddytywności wykorzystać nierówność | ||
| Linia 36: | Linia 36: | ||
'''(2)-(3)''' | '''(2)-(3)''' | ||
Pokazać, że | Pokazać, że | ||
<math> | <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> | ||
są normami, korzystając z definicji normy. | są normami, korzystając z definicji normy. | ||
</div></div> | </div></div> | ||
| Linia 42: | Linia 42: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' | '''(1)''' | ||
Pokażemy, że <math> | Pokażemy, że <math>\|\cdot\|_2</math> jest normą.<br> | ||
Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | ||
| Linia 56: | Linia 56: | ||
</math></center> | </math></center> | ||
Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math>\lambda\in\mathbb{R}</math> | ||
mamy | mamy | ||
| Linia 124: | Linia 124: | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
Pokażemy, że <math> | Pokażemy, że <math>\|\cdot\|_1</math> jest normą.<br> | ||
Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | ||
| Linia 136: | Linia 136: | ||
</math></center> | </math></center> | ||
Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math>\lambda\in\mathbb{R}</math> | ||
mamy | mamy | ||
| Linia 169: | Linia 169: | ||
<br> | <br> | ||
'''(3)''' | '''(3)''' | ||
Pokażemy, że <math> | Pokażemy, że <math>\|\cdot\|_{\infty}</math> jest normą.<br> | ||
Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | ||
| Linia 181: | Linia 181: | ||
</math></center> | </math></center> | ||
Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math>\lambda\in\mathbb{R}</math> | ||
mamy | mamy | ||
| Linia 237: | Linia 237: | ||
</math></center> | </math></center> | ||
więc norma euklidesowa <math> | więc norma euklidesowa <math>\|\cdot\|_2</math> zadaje metrykę euklidesową | ||
<math>d_2.</math> | <math>d_2.</math> | ||
| Linia 249: | Linia 249: | ||
</math></center> | </math></center> | ||
więc norma taksówkowa <math> | więc norma taksówkowa <math>\|\cdot\|_1</math> zadaje metrykę taksówkową | ||
<math>d_2.</math> | <math>d_2.</math> | ||
Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | ||
| Linia 260: | Linia 260: | ||
</math></center> | </math></center> | ||
więc norma maksimowa <math> | więc norma maksimowa <math>\|\cdot\|_{\infty}</math> zadaje metrykę maksimową | ||
<math>d_{\infty}.</math> | <math>d_{\infty}.</math> | ||
</div></div> | </div></div> | ||
| Linia 267: | Linia 267: | ||
Wykazać bezpośrednio równoważność norm: | Wykazać bezpośrednio równoważność norm: | ||
<math> | <math>\|\cdot\|_1</math> (taksówkowej), | ||
<math> | <math>\|\cdot\|_2</math> (euklidesowej) | ||
i <math> | i <math>\|\cdot\|_{\infty}</math> (maksimowej) | ||
w <math> | w <math>\mathbb{R}^N,</math> znajdując optymalne | ||
stałe <math>m_i,M_i>0</math> (<math>i=1,2,3</math>) | stałe <math>m_i,M_i>0</math> (<math>i=1,2,3</math>) | ||
w następujących nierównościach: | w następujących nierównościach: | ||
| Linia 302: | Linia 302: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' Skorzystać jedynie z definicji norm | '''(1)''' Skorzystać jedynie z definicji norm | ||
<math> | <math>\|\cdot\|_2</math> i <math>\|\cdot\|_{\infty},</math> | ||
dla pokazania nierówności i wyznaczenia stałych. | dla pokazania nierówności i wyznaczenia stałych. | ||
Aby pokazać "optymalność" stałych, | Aby pokazać "optymalność" stałych, | ||
| Linia 587: | Linia 587: | ||
Aby pokazać, że zbiór <math>A\cap B</math> jest wypukły, | Aby pokazać, że zbiór <math>A\cap B</math> jest wypukły, | ||
wybierzmy dwa dowolne punkty | wybierzmy dwa dowolne punkty | ||
<math>x,y\in A\cap B</math> oraz <math> | <math>x,y\in A\cap B</math> oraz <math>\lambda\in(0,1).</math> | ||
Ponieważ | Ponieważ | ||
<math>x,y\in A</math> i zbiór <math>A</math> jest wypukły, | <math>x,y\in A</math> i zbiór <math>A</math> jest wypukły, | ||
więc także | więc także | ||
<math> | <math>\lambda x+(1-\lambda)y\in A.</math> | ||
Analogicznie ponieważ | Analogicznie ponieważ | ||
<math>x,y\in B</math> i zbiór <math>B</math> jest wypukły, | <math>x,y\in B</math> i zbiór <math>B</math> jest wypukły, | ||
więc także | więc także | ||
<math> | <math>\lambda x+(1-\lambda)y\in B.</math> | ||
Zatem | Zatem | ||
<math> | <math>\lambda x+(1-\lambda)y\in A\cap B.</math> | ||
Dowodzi to wypukłości zbioru <math>A\cap B.</math><br> | Dowodzi to wypukłości zbioru <math>A\cap B.</math><br> | ||
<br> | <br> | ||
| Linia 606: | Linia 606: | ||
Zbiory <math>A</math> i <math>B</math> są wypukłe, ale | Zbiory <math>A</math> i <math>B</math> są wypukłe, ale | ||
zbiór <math>A\cup B=[0,2]\cup [4,6]</math> nie jest wypukły, | zbiór <math>A\cup B=[0,2]\cup [4,6]</math> nie jest wypukły, | ||
gdyż na przykład dla <math>x=1,y=5</math> i <math> | gdyż na przykład dla <math>x=1,y=5</math> i <math>\lambda=\frac{1}{2}</math> | ||
mamy <math>x,y\in A\cup B, | mamy <math>x,y\in A\cup B,\lambda\in(0,1),</math> | ||
ale <math> | ale <math>\lambda x+(1-\lambda)y=3\not\in A\cup B.</math><br> | ||
<br> | <br> | ||
'''(3)''' | '''(3)''' | ||
| Linia 625: | Linia 625: | ||
Aby pokazać, że zbiór <math>A\times B</math> jest wypukły, | Aby pokazać, że zbiór <math>A\times B</math> jest wypukły, | ||
wybierzmy dwa dowolne punkty | wybierzmy dwa dowolne punkty | ||
<math>(a_1,b_1),(a_2,b_2)\in A\times B</math> oraz <math> | <math>(a_1,b_1),(a_2,b_2)\in A\times B</math> oraz <math>\lambda\in(0,1).</math> | ||
Wówczas | Wówczas | ||
| Linia 672: | Linia 672: | ||
'''(1)''' | '''(1)''' | ||
Pokazać, że <math> | Pokazać, że <math>\|\cdot\|_{\infty}</math> jest normą | ||
w <math>C\big([0,1];\mathbb{R}\big).</math> | w <math>C\big([0,1];\mathbb{R}\big).</math> | ||
Nazywamy ją '''''normą supremową'''''.<br> | Nazywamy ją '''''normą supremową'''''.<br> | ||
| Linia 716: | Linia 716: | ||
</math></center> | </math></center> | ||
Implikacja "<math> | Implikacja "<math>\Longrightarrow</math>" jest oczywista. | ||
W celu udowodnienia implikacji | W celu udowodnienia implikacji | ||
"<math> | "<math>\Longleftarrow</math>" załóżmy, że | ||
<math> | <math>\|f\|_{\infty}=0.</math> | ||
Wówczas | Wówczas | ||
<math> | <math>\sup_{x\in [0,1]}|f(x)|=0.</math> | ||
To oznacza, że | To oznacza, że | ||
<math>|f(x)|=0</math> dla każdego <math>x\in [0,1],</math> czyli | <math>|f(x)|=0</math> dla każdego <math>x\in [0,1],</math> czyli | ||
| Linia 730: | Linia 730: | ||
W celu pokazania jednorodności, niech | W celu pokazania jednorodności, niech | ||
<math>f\in C\big([0,1];\mathbb{R}\big)</math> | <math>f\in C\big([0,1];\mathbb{R}\big)</math> | ||
oraz <math> | oraz <math>\lambda\in \mathbb{R}.</math> | ||
Wówczas | Wówczas | ||
| Linia 768: | Linia 768: | ||
\end{array}</math></center> | \end{array}</math></center> | ||
Aby uzasadnić powyższą nierówność <math> | Aby uzasadnić powyższą nierówność <math>\star,</math> | ||
zauważmy, że | zauważmy, że | ||
| Linia 780: | Linia 780: | ||
zatem biorąc supremum po lewej, stronie nierówność nadal jest | zatem biorąc supremum po lewej, stronie nierówność nadal jest | ||
zachowana i dostajemy <math> | zachowana i dostajemy <math>\star.</math><br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
| Linia 787: | Linia 787: | ||
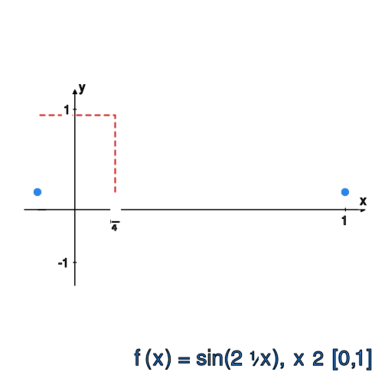
oraz <math>|f_1(x)|=|\sin(2\pi x)|\le 1</math> dla dowolnego | oraz <math>|f_1(x)|=|\sin(2\pi x)|\le 1</math> dla dowolnego | ||
<math>x\in [0,1],</math> zatem | <math>x\in [0,1],</math> zatem | ||
<math> | <math>\|f_1\|_{\infty}=1.</math><br> | ||
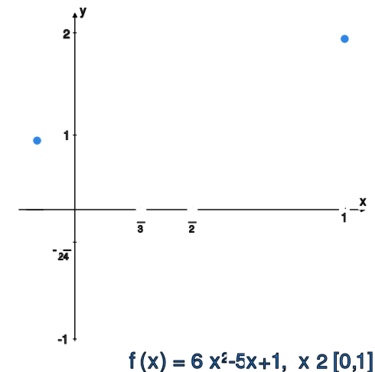
Funkcja kwadratowa na odcinku domkniętym może przyjmować wartość | Funkcja kwadratowa na odcinku domkniętym może przyjmować wartość | ||
| Linia 843: | Linia 843: | ||
<math>C\big([0,1];\mathbb{R}\big)</math> jest zupełna. | <math>C\big([0,1];\mathbb{R}\big)</math> jest zupełna. | ||
W tym celu weźmy dowolny ciąg Cauchy'ego | W tym celu weźmy dowolny ciąg Cauchy'ego | ||
<math> | <math>\{f_n\}\subseteq C\big([0,1];\mathbb{R}\big).</math> | ||
Należy pokazać, że ma on granicę w normie supremowej | Należy pokazać, że ma on granicę w normie supremowej | ||
(a zatem z punktu (3), że jest jednostajnie zbieżny). | (a zatem z punktu (3), że jest jednostajnie zbieżny). | ||
Zauważmy, że dla dowolnego <math>x\in [0,1],</math> | Zauważmy, że dla dowolnego <math>x\in [0,1],</math> | ||
ciąg liczbowy <math> | ciąg liczbowy <math>\{f_n(x)\}</math> jest ciągiem Cauchy'ego | ||
(w <math> | (w <math>\mathbb{R}</math>), | ||
a zatem jest zbieżny, powiedzmy do <math>f(x)</math> | a zatem jest zbieżny, powiedzmy do <math>f(x)</math> | ||
(korzystamy z zupełności <math> | (korzystamy z zupełności <math>\mathbb{R}</math>). | ||
Zatem <math>f</math> jest granicą punktową ciągu funkcyjnego | Zatem <math>f</math> jest granicą punktową ciągu funkcyjnego | ||
<math> | <math>\{f_n\}.</math> | ||
Ustalmy <math> | Ustalmy <math>\varepsilon>0.</math> | ||
Z warunku Cauchy'ego wynika, że | Z warunku Cauchy'ego wynika, że | ||
| Linia 880: | Linia 880: | ||
Zatem pokazaliśmy, że <math>f\rightrightarrows f,</math> | Zatem pokazaliśmy, że <math>f\rightrightarrows f,</math> | ||
czyli ciąg <math> | czyli ciąg <math>\{f_n\}</math> jest zbieżny w normie supremowej. | ||
W końcu korzystając | W końcu korzystając | ||
z twierdzenia o ciągłości granicy jednostajnie zbieżnego ciągu funkcji | z twierdzenia o ciągłości granicy jednostajnie zbieżnego ciągu funkcji | ||
| Linia 890: | Linia 890: | ||
<span id="cw_3_6">{{cwiczenie|3.6.|| | <span id="cw_3_6">{{cwiczenie|3.6.|| | ||
Niech <math> | Niech <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> oznaczają odpowiednio | ||
normę taksówkową i maksimową w <math> | normę taksówkową i maksimową w <math>\mathbb{R}^N.</math> | ||
Pokazać, że | Pokazać, że | ||
| Linia 899: | Linia 899: | ||
</math></center> | </math></center> | ||
jest normą w <math> | jest normą w <math>\mathbb{R}^N.</math> | ||
Dla <math>N=2</math> narysować kulę | Dla <math>N=2</math> narysować kulę | ||
<math>K\big((0,0),1\big)\subseteq\mathbb{R}^2</math> w tej normie. | <math>K\big((0,0),1\big)\subseteq\mathbb{R}^2</math> w tej normie. | ||
| Linia 906: | Linia 906: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Korzystając z definicji norm | Korzystając z definicji norm | ||
<math> | <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math>, | ||
pokazać, że <math> | pokazać, że <math>\|\cdot\|_{\square}</math> | ||
jest normą. | jest normą. | ||
</div></div> | </div></div> | ||
| Linia 915: | Linia 915: | ||
Niech <math>x\in\mathbb{R}^N.</math> | Niech <math>x\in\mathbb{R}^N.</math> | ||
Pokażemy, że | Pokażemy, że | ||
<math> | <math>\|x\|_{\square}=0\Longleftrightarrow x=\Theta.</math> | ||
Implikacja "<math> | Implikacja "<math>\Longleftarrow</math>" jest oczywista. | ||
W celu udowodnienia implikacji | W celu udowodnienia implikacji | ||
"<math> | "<math>\Longrightarrow</math>" załóżmy, że | ||
<math> | <math>\|x\|_{\square}=0.</math> | ||
Wówczas | Wówczas | ||
<math>2\|x\|_1+\|x\|_{\infty}=0,</math> czyli | <math>2\|x\|_1+\|x\|_{\infty}=0,</math> czyli | ||
<math> | <math>\|x\|_1=0</math> i <math>\|x\|_{\infty}=0.</math> | ||
Ponieważ <math> | Ponieważ <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> | ||
są normami, więc <math>x=\Theta.</math> | są normami, więc <math>x=\Theta.</math> | ||
W celu pokazania jednorodności niech | W celu pokazania jednorodności niech | ||
<math>x\in \mathbb{R}^N</math> oraz <math> | <math>x\in \mathbb{R}^N</math> oraz <math>\lambda\in\mathbb{R}.</math> | ||
Wówczas | Wówczas | ||
| Linia 974: | Linia 974: | ||
</center> | </center> | ||
Co kończy dowód, że <math> | Co kończy dowód, że <math>\|\cdot\|_{\square}</math> jest norma w | ||
<math> | <math>\mathbb{R}^N.</math><br> | ||
Aby narysować kulę | Aby narysować kulę | ||
| Linia 996: | Linia 996: | ||
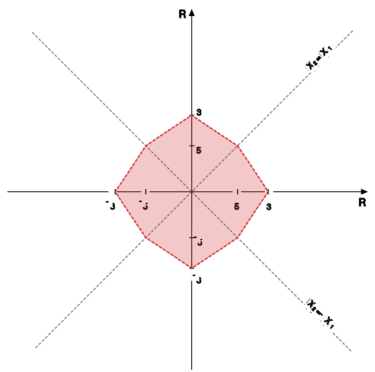
Zbiór punktów <math>(x_1,x_2)\in\mathbb{R}^2</math> spełniających | Zbiór punktów <math>(x_1,x_2)\in\mathbb{R}^2</math> spełniających | ||
nierówność <math> | nierówność <math>\|(x_1,x_2)\|_{\square}<1</math> dostajemy, rozpisując | ||
nierówności w poszczególnych ćwiartkach układu współrzędnych, | nierówności w poszczególnych ćwiartkach układu współrzędnych, | ||
dostajemy ośmiokąt jak na rysunku obok.<br> | dostajemy ośmiokąt jak na rysunku obok.<br> | ||
| Linia 1003: | Linia 1003: | ||
<span id="cw_3_7">{{cwiczenie|3.7.|| | <span id="cw_3_7">{{cwiczenie|3.7.|| | ||
Niech <math> | Niech <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> oznaczają odpowiednio | ||
normę taksówkową i maksimową w <math> | normę taksówkową i maksimową w <math>\mathbb{R}^N.</math> | ||
Sprawdzić, czy | Sprawdzić, czy | ||
| Linia 1012: | Linia 1012: | ||
</math></center> | </math></center> | ||
jest normą w <math> | jest normą w <math>\mathbb{R}^2.</math> | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Pokazać brak subaddytywności dla <math> | Pokazać brak subaddytywności dla <math>\|\cdot\|_{\circ}.</math> | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Pokażemy, że <math> | Pokażemy, że <math>\|\cdot\|_{\circ}</math> nie spełnia warunku | ||
subaddytywności. | subaddytywności. | ||
Dla wektorów | Dla wektorów | ||
<math>x=(1,0)</math> i <math>y(0,1)</math> w <math> | <math>x=(1,0)</math> i <math>y(0,1)</math> w <math>\mathbb{R}^2</math> mamy | ||
<center><math>\|x+y\|_{\circ} | <center><math>\|x+y\|_{\circ} | ||
| Linia 1046: | Linia 1046: | ||
Zatem | Zatem | ||
<math> | <math>\|x+y\|_{\circ}\not\le\|x\|_{\circ}+\|y\|_{\circ}.</math> | ||
Jako ciekawostkę proponujemy sprawdzenie, że dwa pierwsze | Jako ciekawostkę proponujemy sprawdzenie, że dwa pierwsze | ||
warunki w definicji normy zachodzą dla | warunki w definicji normy zachodzą dla | ||
<math> | <math>\|\cdot\|_{\circ}.</math> | ||
</div></div> | </div></div> | ||
<span id="cw_3_8">{{cwiczenie|3.8.|| | <span id="cw_3_8">{{cwiczenie|3.8.|| | ||
W <math> | W <math>\mathbb{R}^2</math> wprowadzamy | ||
<center><math>\big((x_1,x_2)|(y_1,y_2)\big)_{\triangle} | <center><math>\big((x_1,x_2)|(y_1,y_2)\big)_{\triangle} | ||
| Linia 1064: | Linia 1064: | ||
'''(1)''' | '''(1)''' | ||
Pokazać, że <math> | Pokazać, że <math>\big(\cdot |\cdot \big)_{\triangle}</math> jest | ||
iloczynem skalarnym w <math> | iloczynem skalarnym w <math>\mathbb{R}^2.</math><br> | ||
'''(2)''' | '''(2)''' | ||
Jak wygląda <math> | Jak wygląda <math>\|\cdot\|_{\triangle}</math> | ||
norma zadana przez ten iloczyn skalarny? | norma zadana przez ten iloczyn skalarny? | ||
Obliczyć <math> | Obliczyć <math>\|(4,5)\|_{\triangle}.</math><br> | ||
'''(3)''' | '''(3)''' | ||
Dane są dwa wektory | Dane są dwa wektory | ||
| Linia 1122: | Linia 1122: | ||
pokazaliśmy więc punkt (1) definicji iloczynu skalarnego. | pokazaliśmy więc punkt (1) definicji iloczynu skalarnego. | ||
Niech <math>x=(x_1,x_2),y=(y_1,y_2)\in X</math> oraz <math> | Niech <math>x=(x_1,x_2),y=(y_1,y_2)\in X</math> oraz <math>\lambda\in \mathbb{R}.</math> | ||
Wówczas | Wówczas | ||
| Linia 1128: | Linia 1128: | ||
\begin{array}{lll} | \begin{array}{lll} | ||
\big(\lambda(x_1,x_2)|(y_1,y_2)\big)_{\triangle} | \big(\lambda(x_1,x_2)|(y_1,y_2)\big)_{\triangle} | ||
&=& | &=& | ||
\big((\lambda x_1,\lambda x_2)|(y_1,y_2)\big)_{\triangle} | \big((\lambda x_1,\lambda x_2)|(y_1,y_2)\big)_{\triangle} | ||
= | = | ||
3\lambda x_1y_1+5\lambda x_2y_2\\ | 3\lambda x_1y_1+5\lambda x_2y_2\\ | ||
&=& | &=& | ||
\lambda\big(3x_1y_1+5x_2y_2\big) | \lambda\big(3x_1y_1+5x_2y_2\big) | ||
= | = | ||
| Linia 1178: | Linia 1178: | ||
Kończy to dowód faktu, że | Kończy to dowód faktu, że | ||
<math>(\cdot|\cdot)_{\triangle}</math> jest | <math>(\cdot|\cdot)_{\triangle}</math> jest | ||
iloczynem skalarnym w <math> | iloczynem skalarnym w <math>\mathbb{R}^2.</math><br> | ||
<br> | <br> | ||
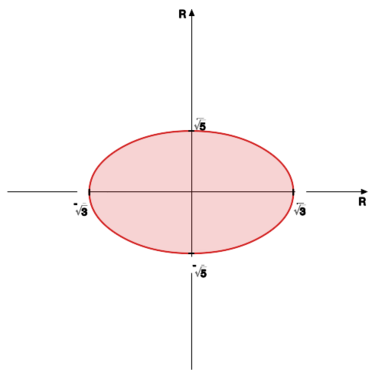
[[File:AM2.M03.C_R06.svg|375x375px|thumb|right|Kula w metryce zadanej przez iloczyn skalarny z ćwiczenia 3.8.]] | [[File:AM2.M03.C_R06.svg|375x375px|thumb|right|Kula w metryce zadanej przez iloczyn skalarny z ćwiczenia 3.8.]] | ||
'''(2)''' | '''(2)''' | ||
Ponieważ <math>(\cdot|\cdot)_{\triangle},</math> | Ponieważ <math>(\cdot|\cdot)_{\triangle},</math> | ||
więc norma <math> | więc norma <math>\|\cdot\|_{\triangle}</math> | ||
zadana przez ten iloczyn skalarny | zadana przez ten iloczyn skalarny | ||
dla dowolnego <math>x=(x_1,x_2)\in\mathbb{R}^2</math> | dla dowolnego <math>x=(x_1,x_2)\in\mathbb{R}^2</math> | ||
| Linia 1253: | Linia 1253: | ||
<math>(x_1,x_2)\in\mathbb{R}^2</math> | <math>(x_1,x_2)\in\mathbb{R}^2</math> | ||
spełniających równanie | spełniających równanie | ||
<math> | <math>\frac{x_1^2}{a^2}+\frac{x_2^2}{b^2}=1</math> jest elipsą o półosiach | ||
wielkich <math>a</math> i <math>b.</math> | wielkich <math>a</math> i <math>b.</math> | ||
Zatem w naszym przypadku | Zatem w naszym przypadku | ||
| Linia 1259: | Linia 1259: | ||
<math>\frac{x_1^2}{\frac{1}{3}}+\frac{x_2^2}{\frac{1}{5}}<1</math> | <math>\frac{x_1^2}{\frac{1}{3}}+\frac{x_2^2}{\frac{1}{5}}<1</math> | ||
jest wnętrzem elipsy o półosiach wielkich | jest wnętrzem elipsy o półosiach wielkich | ||
<math> | <math>\frac{1}{\sqrt{3}}</math> | ||
oraz <math> | oraz <math>\frac{1}{\sqrt{5}}.</math><br> | ||
</div></div> | </div></div> | ||
| Linia 1272: | Linia 1272: | ||
<math>f</math> jest ciągła;<br> | <math>f</math> jest ciągła;<br> | ||
'''(ii)''' | '''(ii)''' | ||
<math> | <math>\exists x_0\in X</math>: <math>f</math> jest ciągła w <math>x_0</math>;<br> | ||
'''(iii)''' | '''(iii)''' | ||
<math>f</math> jest ciągła w <math> | <math>f</math> jest ciągła w <math>\Theta\in X</math> | ||
(<math>\Theta</math> oznacza wektor zerowy przestrzeni wektorowej <math>X</math>);<br> | (<math>\Theta</math> oznacza wektor zerowy przestrzeni wektorowej <math>X</math>);<br> | ||
'''(iv)''' | '''(iv)''' | ||
<math> | <math>\exists M\ge 0\ \ \forall x\in X: | ||
\|x\|_X\le 1\ \Longrightarrow \big\|f(x)\big\|_Y\le M</math> | \|x\|_X\le 1\ \Longrightarrow \big\|f(x)\big\|_Y\le M</math> | ||
(to znaczy odwzorowanie <math>f</math> jest ograniczone na domkniętej kuli o promieniu <math>1</math>);<br> | (to znaczy odwzorowanie <math>f</math> jest ograniczone na domkniętej kuli o promieniu <math>1</math>);<br> | ||
'''(v)''' | '''(v)''' | ||
<math> | <math>\exists c\ge 0\ \ \forall x\in X: | ||
\big\|f(x)\big\|_Y\le c\|x\|_X</math> | \big\|f(x)\big\|_Y\le c\|x\|_X</math> | ||
(warunek ten nazywa się '''''ograniczonością dla odwzorowania liniowego''''');<br> | (warunek ten nazywa się '''''ograniczonością dla odwzorowania liniowego''''');<br> | ||
| Linia 1301: | Linia 1301: | ||
Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | ||
jest ciągła w pewnym punkcie <math>x_0\in X.</math> | jest ciągła w pewnym punkcie <math>x_0\in X.</math> | ||
Pokażemy, że jest ciągła w <math> | Pokażemy, że jest ciągła w <math>\Theta\in X.</math> | ||
Ustalmy dowolne <math> | Ustalmy dowolne <math>\varepsilon>0.</math> | ||
Z definicji Cauchy'ego ciągłości funkcji w punkcie wiemy, że | Z definicji Cauchy'ego ciągłości funkcji w punkcie wiemy, że | ||
| Linia 1313: | Linia 1313: | ||
Dla dowolnego <math>z\in X</math> takiego, że | Dla dowolnego <math>z\in X</math> takiego, że | ||
<math> | <math>\|z\|_X\le\delta</math> niech | ||
<math>x=z+x_0.</math> | <math>x=z+x_0.</math> | ||
Wówczas <math> | Wówczas <math>\|x-x_0\|_X=\|z\|_X\le\delta,</math> a zatem korzystając z | ||
powyższej implikacji, dostajemy, że | powyższej implikacji, dostajemy, że | ||
<math> | <math>\|f(z)\|_Y=\|f(x-x_0)\|_Y=\|f(x)-f(x_0)\|_Y\le\varepsilon.</math> | ||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
| Linia 1326: | Linia 1326: | ||
</math></center> | </math></center> | ||
a to oznacza ciągłość funkcji <math>f</math> w punkcie <math> | a to oznacza ciągłość funkcji <math>f</math> w punkcie <math>\Theta.</math><br> | ||
<br> | <br> | ||
"<math>(iii)\Longrightarrow(iv)</math>"<br> | "<math>(iii)\Longrightarrow(iv)</math>"<br> | ||
Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | ||
jest ciągła w punkcie <math> | jest ciągła w punkcie <math>\Theta.</math> | ||
Ustalmy <math> | Ustalmy <math>\varepsilon=1.</math> | ||
Wówczas | Wówczas | ||
| Linia 1341: | Linia 1341: | ||
Niech <math>M:=\frac{1}{\delta}.</math> | Niech <math>M:=\frac{1}{\delta}.</math> | ||
Wówczas dla <math>x\in X\setminus\{\Theta\}</math> takich, że <math> | Wówczas dla <math>x\in X\setminus\{\Theta\}</math> takich, że <math>\|x\|_X\le 1</math> | ||
mamy | mamy | ||
| Linia 1352: | Linia 1352: | ||
Korzystając z faktów, że | Korzystając z faktów, że | ||
<math> | <math>\|x\|_X\le 1</math> oraz | ||
<math> | <math>\|\delta x\|_X=\delta\|x\|_X\le\delta</math> | ||
i z powyższej implikacji, | i z powyższej implikacji, | ||
dostajemy, że | dostajemy, że | ||
| Linia 1395: | Linia 1395: | ||
</math></center> | </math></center> | ||
Ponieważ <math> | Ponieważ <math>\bigg\|\frac{x}{\|x\|_X}\bigg\|_X=1,</math> | ||
więc możemy skorzystać z założenia, otrzymując | więc możemy skorzystać z założenia, otrzymując | ||
| Linia 1424: | Linia 1424: | ||
W celu pokazania jednostajnej ciągłości funkcji <math>f</math> | W celu pokazania jednostajnej ciągłości funkcji <math>f</math> | ||
ustalmy dowolne <math> | ustalmy dowolne <math>\varepsilon>0.</math> | ||
Niech | Niech | ||
<math> | <math>\delta:=\frac{\varepsilon}{c}.</math> | ||
Wówczas dla dowolnych <math>x,z\in X</math> | Wówczas dla dowolnych <math>x,z\in X</math> | ||
takich, że <math> | takich, że <math>\|x-z\|_X\le\delta,</math> | ||
korzystając z założenia, mamy | korzystając z założenia, mamy | ||
Wersja z 10:16, 28 sie 2023
Norma. Iloczyn skalarny
Ćwiczenie 3.1.
W przestrzeni wektorowej definiujemy:
Pokazać, że oraz są normami (nazywamy je odpowiednio normą euklidesową, normą taksówkową oraz normą maksimową).
Ćwiczenie 3.2.
Pokazać, że norma euklidesowa zadaje metrykę euklidesową, norma taksówkowa zadaje metrykę taksówkową, a norma maksimowa zadaje metrykę maksimową.
Ćwiczenie 3.3.
Wykazać bezpośrednio równoważność norm: (taksówkowej), (euklidesowej) i (maksimowej) w znajdując optymalne stałe () w następujących nierównościach:
Ćwiczenie 3.4.
Niech i będą dwiema przestrzeniami wektorowymi.
Które z poniższych stwierdzeń są prawdziwe?
(Dla każdego podać dowód lub kontrprzykład).
(1)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(2)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(3)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(4)
Jeśli zbiory i
są wypukłe, to zbiór jest wypukły w
Ćwiczenie 3.5.
W przestrzeni wektorowej funkcji ciągłych na przedziale definiujemy:
(1)
Pokazać, że jest normą
w
Nazywamy ją normą supremową.
(2)
Obliczyć normę supremową dla funkcji:
oraz
(3)
Udowodnić, że zbieżność w normie supremowej pokrywa się ze
zbieżnością jednostajną dla funkcji ciągłych na
przedziale
(4) Pokazać, że z normą supremową jest przestrzenią Banacha.
(Punkty (3) i (4) są nadobowiązkowe. Potrzebne są tu pewne pojęcia z następnego wykładu. Do zadania można wrócić po następnym wykładzie).
Ćwiczenie 3.6.
Niech i oznaczają odpowiednio normę taksówkową i maksimową w Pokazać, że
jest normą w Dla narysować kulę w tej normie.
Ćwiczenie 3.7.
Niech i oznaczają odpowiednio normę taksówkową i maksimową w Sprawdzić, czy
jest normą w
Ćwiczenie 3.8.
W wprowadzamy
(1)
Pokazać, że jest
iloczynem skalarnym w
(2)
Jak wygląda
norma zadana przez ten iloczyn skalarny?
Obliczyć
(3)
Dane są dwa wektory
i
Dobrać parametr tak, aby
(oczywiście w rozważanym iloczynie skalarnym).
(4)
Narysować kulę
w metryce zadanej przez ten
iloczyn skalarny.
Ćwiczenie 3.9.
(Zadanie nadobowiązkowe.)
Niech będą dwiema przestrzeniami unormowanymi oraz
odwzorowaniem liniowym.
Udowodnić, że następujące warunki są
równoważne:
(i)
jest ciągła;
(ii)
: jest ciągła w ;
(iii)
jest ciągła w
( oznacza wektor zerowy przestrzeni wektorowej );
(iv)
(to znaczy odwzorowanie jest ograniczone na domkniętej kuli o promieniu );
(v)
(warunek ten nazywa się ograniczonością dla odwzorowania liniowego);
(vi)
jest jednostajnie ciągła.