Analiza matematyczna 2/Ćwiczenia 3: Norma. Iloczyn skalarny: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „.</math>” na „</math>.” |
|||
| Linia 238: | Linia 238: | ||
więc norma euklidesowa <math>\|\cdot\|_2</math> zadaje metrykę euklidesową | więc norma euklidesowa <math>\|\cdot\|_2</math> zadaje metrykę euklidesową | ||
<math>d_2 | <math>d_2</math>. | ||
Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | ||
| Linia 250: | Linia 250: | ||
więc norma taksówkowa <math>\|\cdot\|_1</math> zadaje metrykę taksówkową | więc norma taksówkowa <math>\|\cdot\|_1</math> zadaje metrykę taksówkową | ||
<math>d_2 | <math>d_2</math>. | ||
Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | ||
| Linia 335: | Linia 335: | ||
czyli | czyli | ||
<math>m_1=\frac{1}{\sqrt{N}} | <math>m_1=\frac{1}{\sqrt{N}}</math>. | ||
Aby pokazać, że stała <math>m_1</math> jest "optymalna" | Aby pokazać, że stała <math>m_1</math> jest "optymalna" | ||
(to znaczy największa z możliwych), zauważmy, że dla wektora | (to znaczy największa z możliwych), zauważmy, że dla wektora | ||
| Linia 371: | Linia 371: | ||
</math></center> | </math></center> | ||
czyli <math>M_1=1 | czyli <math>M_1=1</math>. Aby pokazać, że stała <math>M_1</math> jest "optymalna" | ||
(to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | (to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | ||
<math>x_0=(1,0,\ldots,0)</math> mamy | <math>x_0=(1,0,\ldots,0)</math> mamy | ||
| Linia 406: | Linia 406: | ||
czyli | czyli | ||
<math>m_2=\frac{1}{N} | <math>m_2=\frac{1}{N}</math>. | ||
Aby pokazać, że stała <math>m_2</math> jest "optymalna" | Aby pokazać, że stała <math>m_2</math> jest "optymalna" | ||
(to znaczy największa z możliwych), zauważmy, że dla wektora | (to znaczy największa z możliwych), zauważmy, że dla wektora | ||
| Linia 440: | Linia 440: | ||
</math></center> | </math></center> | ||
czyli <math>M_1=1 | czyli <math>M_1=1</math>. Aby pokazać, że stała <math>M_1</math> jest "optymalna" | ||
(to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | (to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | ||
<math>x_0=(1,0,\ldots,0)</math> mamy | <math>x_0=(1,0,\ldots,0)</math> mamy | ||
| Linia 502: | Linia 502: | ||
czyli | czyli | ||
<math>m_3=\frac{1}{\sqrt{N}} | <math>m_3=\frac{1}{\sqrt{N}}</math>. | ||
Aby pokazać, że stała <math>m_3</math> jest "optymalna" | Aby pokazać, że stała <math>m_3</math> jest "optymalna" | ||
(to znaczy największa z możliwych), zauważmy, że dla wektora | (to znaczy największa z możliwych), zauważmy, że dla wektora | ||
| Linia 536: | Linia 536: | ||
</math></center> | </math></center> | ||
czyli <math>M_3=1 | czyli <math>M_3=1</math>. Aby pokazać, że stała <math>M_3</math> jest "optymalna" | ||
(to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | (to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | ||
<math>x_0=(1,0,\ldots,0)</math> mamy | <math>x_0=(1,0,\ldots,0)</math> mamy | ||
| Linia 562: | Linia 562: | ||
'''(4)''' | '''(4)''' | ||
Jeśli zbiory <math>A\subseteq X</math> i <math>B\subseteq Y</math> | Jeśli zbiory <math>A\subseteq X</math> i <math>B\subseteq Y</math> | ||
są wypukłe, to zbiór <math>A\times B</math> jest wypukły w <math>X\times Y | są wypukłe, to zbiór <math>A\times B</math> jest wypukły w <math>X\times Y</math>.<br> | ||
}}</span> | }}</span> | ||
| Linia 587: | Linia 587: | ||
Aby pokazać, że zbiór <math>A\cap B</math> jest wypukły, | Aby pokazać, że zbiór <math>A\cap B</math> jest wypukły, | ||
wybierzmy dwa dowolne punkty | wybierzmy dwa dowolne punkty | ||
<math>x,y\in A\cap B</math> oraz <math>\lambda\in(0,1) | <math>x,y\in A\cap B</math> oraz <math>\lambda\in(0,1)</math>. | ||
Ponieważ | Ponieważ | ||
<math>x,y\in A</math> i zbiór <math>A</math> jest wypukły, | <math>x,y\in A</math> i zbiór <math>A</math> jest wypukły, | ||
więc także | więc także | ||
<math>\lambda x+(1-\lambda)y\in A | <math>\lambda x+(1-\lambda)y\in A</math>. | ||
Analogicznie ponieważ | Analogicznie ponieważ | ||
<math>x,y\in B</math> i zbiór <math>B</math> jest wypukły, | <math>x,y\in B</math> i zbiór <math>B</math> jest wypukły, | ||
więc także | więc także | ||
<math>\lambda x+(1-\lambda)y\in B | <math>\lambda x+(1-\lambda)y\in B</math>. | ||
Zatem | Zatem | ||
<math>\lambda x+(1-\lambda)y\in A\cap B | <math>\lambda x+(1-\lambda)y\in A\cap B</math>. | ||
Dowodzi to wypukłości zbioru <math>A\cap B | Dowodzi to wypukłości zbioru <math>A\cap B</math>.<br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
Stwierdzenie to nie jest prawdziwe. | Stwierdzenie to nie jest prawdziwe. | ||
Dla przykładu niech | Dla przykładu niech | ||
<math>X=\mathbb{R},A=[0,2]</math> oraz <math>B=[4,6] | <math>X=\mathbb{R},A=[0,2]</math> oraz <math>B=[4,6]</math>. | ||
Zbiory <math>A</math> i <math>B</math> są wypukłe, ale | Zbiory <math>A</math> i <math>B</math> są wypukłe, ale | ||
zbiór <math>A\cup B=[0,2]\cup [4,6]</math> nie jest wypukły, | zbiór <math>A\cup B=[0,2]\cup [4,6]</math> nie jest wypukły, | ||
gdyż na przykład dla <math>x=1,y=5</math> i <math>\lambda=\frac{1}{2}</math> | gdyż na przykład dla <math>x=1,y=5</math> i <math>\lambda=\frac{1}{2}</math> | ||
mamy <math>x,y\in A\cup B,\lambda\in(0,1),</math> | mamy <math>x,y\in A\cup B,\lambda\in(0,1),</math> | ||
ale <math>\lambda x+(1-\lambda)y=3\not\in A\cup B | ale <math>\lambda x+(1-\lambda)y=3\not\in A\cup B</math>.<br> | ||
<br> | <br> | ||
'''(3)''' | '''(3)''' | ||
Stwierdzenie to nie jest prawdziwe. | Stwierdzenie to nie jest prawdziwe. | ||
Dla przykładu niech | Dla przykładu niech | ||
<math>X=\mathbb{R},A=[0,6]</math> oraz <math>B=(2,4) | <math>X=\mathbb{R},A=[0,6]</math> oraz <math>B=(2,4)</math>. | ||
Zbiory <math>A</math> i <math>B</math> są wypukłe, ale | Zbiory <math>A</math> i <math>B</math> są wypukłe, ale | ||
zbiór <math>A\cup B=[0,2]\cup [4,6]</math> nie jest wypukły | zbiór <math>A\cup B=[0,2]\cup [4,6]</math> nie jest wypukły | ||
| Linia 625: | Linia 625: | ||
Aby pokazać, że zbiór <math>A\times B</math> jest wypukły, | Aby pokazać, że zbiór <math>A\times B</math> jest wypukły, | ||
wybierzmy dwa dowolne punkty | wybierzmy dwa dowolne punkty | ||
<math>(a_1,b_1),(a_2,b_2)\in A\times B</math> oraz <math>\lambda\in(0,1) | <math>(a_1,b_1),(a_2,b_2)\in A\times B</math> oraz <math>\lambda\in(0,1)</math>. | ||
Wówczas | Wówczas | ||
| Linia 673: | Linia 673: | ||
'''(1)''' | '''(1)''' | ||
Pokazać, że <math>\|\cdot\|_{\infty}</math> jest normą | Pokazać, że <math>\|\cdot\|_{\infty}</math> jest normą | ||
w <math>C\big([0,1];\mathbb{R}\big) | w <math>C\big([0,1];\mathbb{R}\big)</math>. | ||
Nazywamy ją '''''normą supremową'''''.<br> | Nazywamy ją '''''normą supremową'''''.<br> | ||
'''(2)''' | '''(2)''' | ||
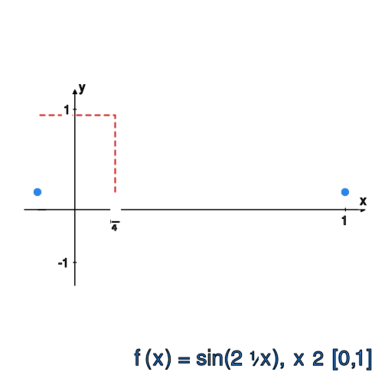
Obliczyć normę supremową dla funkcji: | Obliczyć normę supremową dla funkcji: | ||
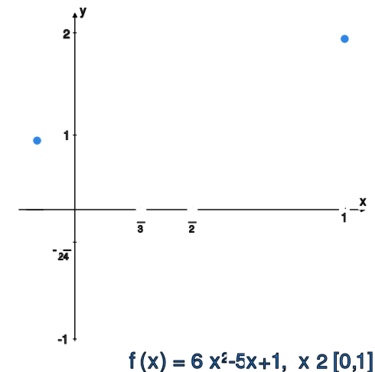
<math>f_1(x)=\sin(2\pi x)</math> oraz | <math>f_1(x)=\sin(2\pi x)</math> oraz | ||
<math>f_2(x)=6x^2-5x+1 | <math>f_2(x)=6x^2-5x+1</math>.<br> | ||
'''(3)''' | '''(3)''' | ||
Udowodnić, że zbieżność w normie supremowej pokrywa się ze | Udowodnić, że zbieżność w normie supremowej pokrywa się ze | ||
zbieżnością jednostajną dla funkcji ciągłych na | zbieżnością jednostajną dla funkcji ciągłych na | ||
przedziale <math>[0,1] | przedziale <math>[0,1]</math>.<br> | ||
'''(4)''' | '''(4)''' | ||
| Linia 699: | Linia 699: | ||
definicji normy.<br> | definicji normy.<br> | ||
'''(2)''' Wyznaczyć największą wartość funkcji | '''(2)''' Wyznaczyć największą wartość funkcji | ||
<math>|f_1|</math> i <math>|f_2|</math> na przedziale <math>[0,1] | <math>|f_1|</math> i <math>|f_2|</math> na przedziale <math>[0,1]</math>.<br> | ||
'''(3)''' Wynika wprost z obu rozważanych definicji.<br> | '''(3)''' Wynika wprost z obu rozważanych definicji.<br> | ||
'''(4)''' Wykorzystać punkt (3) i twierdzenie | '''(4)''' Wykorzystać punkt (3) i twierdzenie | ||
| Linia 719: | Linia 719: | ||
W celu udowodnienia implikacji | W celu udowodnienia implikacji | ||
"<math>\Longleftarrow</math>" załóżmy, że | "<math>\Longleftarrow</math>" załóżmy, że | ||
<math>\|f\|_{\infty}=0 | <math>\|f\|_{\infty}=0</math>. | ||
Wówczas | Wówczas | ||
<math>\sup_{x\in [0,1]}|f(x)|=0 | <math>\sup_{x\in [0,1]}|f(x)|=0</math>. | ||
To oznacza, że | To oznacza, że | ||
<math>|f(x)|=0</math> dla każdego <math>x\in [0,1],</math> czyli | <math>|f(x)|=0</math> dla każdego <math>x\in [0,1],</math> czyli | ||
| Linia 730: | Linia 730: | ||
W celu pokazania jednorodności, niech | W celu pokazania jednorodności, niech | ||
<math>f\in C\big([0,1];\mathbb{R}\big)</math> | <math>f\in C\big([0,1];\mathbb{R}\big)</math> | ||
oraz <math>\lambda\in \mathbb{R} | oraz <math>\lambda\in \mathbb{R}</math>. | ||
Wówczas | Wówczas | ||
| Linia 750: | Linia 750: | ||
Aby pokazać subaddytywność, niech | Aby pokazać subaddytywność, niech | ||
<math>f,g\in C\big([0,1];\mathbb{R}\big) | <math>f,g\in C\big([0,1];\mathbb{R}\big)</math>. | ||
Wówczas | Wówczas | ||
| Linia 780: | Linia 780: | ||
zatem biorąc supremum po lewej, stronie nierówność nadal jest | zatem biorąc supremum po lewej, stronie nierówność nadal jest | ||
zachowana i dostajemy <math>\star | zachowana i dostajemy <math>\star</math>.<br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
| Linia 787: | Linia 787: | ||
oraz <math>|f_1(x)|=|\sin(2\pi x)|\le 1</math> dla dowolnego | oraz <math>|f_1(x)|=|\sin(2\pi x)|\le 1</math> dla dowolnego | ||
<math>x\in [0,1],</math> zatem | <math>x\in [0,1],</math> zatem | ||
<math>\|f_1\|_{\infty}=1 | <math>\|f_1\|_{\infty}=1</math>.<br> | ||
Funkcja kwadratowa na odcinku domkniętym może przyjmować wartość | Funkcja kwadratowa na odcinku domkniętym może przyjmować wartość | ||
| Linia 794: | Linia 794: | ||
Wierzchołek paraboli ma współrzędne | Wierzchołek paraboli ma współrzędne | ||
<math>(p,q)=\bigg(\frac{-b}{2a},\frac{-\Delta}{4a}\bigg) | <math>(p,q)=\bigg(\frac{-b}{2a},\frac{-\Delta}{4a}\bigg) | ||
=\bigg(\frac{5}{12},-\frac{1}{24}\bigg) | =\bigg(\frac{5}{12},-\frac{1}{24}\bigg)</math>. | ||
Na końcach przedziału mamy wartości | Na końcach przedziału mamy wartości | ||
<math>f_2(0)=1,f_2(1)=2,</math> zatem | <math>f_2(0)=1,f_2(1)=2,</math> zatem | ||
| Linia 843: | Linia 843: | ||
<math>C\big([0,1];\mathbb{R}\big)</math> jest zupełna. | <math>C\big([0,1];\mathbb{R}\big)</math> jest zupełna. | ||
W tym celu weźmy dowolny ciąg Cauchy'ego | W tym celu weźmy dowolny ciąg Cauchy'ego | ||
<math>\{f_n\}\subseteq C\big([0,1];\mathbb{R}\big) | <math>\{f_n\}\subseteq C\big([0,1];\mathbb{R}\big)</math>. | ||
Należy pokazać, że ma on granicę w normie supremowej | Należy pokazać, że ma on granicę w normie supremowej | ||
(a zatem z punktu (3), że jest jednostajnie zbieżny). | (a zatem z punktu (3), że jest jednostajnie zbieżny). | ||
| Linia 852: | Linia 852: | ||
(korzystamy z zupełności <math>\mathbb{R}</math>). | (korzystamy z zupełności <math>\mathbb{R}</math>). | ||
Zatem <math>f</math> jest granicą punktową ciągu funkcyjnego | Zatem <math>f</math> jest granicą punktową ciągu funkcyjnego | ||
<math>\{f_n\} | <math>\{f_n\}</math>. | ||
Ustalmy <math>\varepsilon>0 | Ustalmy <math>\varepsilon>0</math>. | ||
Z warunku Cauchy'ego wynika, że | Z warunku Cauchy'ego wynika, że | ||
| Linia 885: | Linia 885: | ||
ciągłych | ciągłych | ||
(patrz [[Analiza matematyczna 2/Wykład 4: Ciągi i szeregi funkcyjne. Szereg Taylora#tw_4_6|twierdzenie 4.6.]]), | (patrz [[Analiza matematyczna 2/Wykład 4: Ciągi i szeregi funkcyjne. Szereg Taylora#tw_4_6|twierdzenie 4.6.]]), | ||
mamy, że <math>f\in C\big([0,1];\mathbb{R}\big) | mamy, że <math>f\in C\big([0,1];\mathbb{R}\big)</math>. | ||
</div></div> | </div></div> | ||
| Linia 891: | Linia 891: | ||
Niech <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> oznaczają odpowiednio | Niech <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> oznaczają odpowiednio | ||
normę taksówkową i maksimową w <math>\mathbb{R}^N | normę taksówkową i maksimową w <math>\mathbb{R}^N</math>. | ||
Pokazać, że | Pokazać, że | ||
| Linia 899: | Linia 899: | ||
</math></center> | </math></center> | ||
jest normą w <math>\mathbb{R}^N | jest normą w <math>\mathbb{R}^N</math>. | ||
Dla <math>N=2</math> narysować kulę | Dla <math>N=2</math> narysować kulę | ||
<math>K\big((0,0),1\big)\subseteq\mathbb{R}^2</math> w tej normie. | <math>K\big((0,0),1\big)\subseteq\mathbb{R}^2</math> w tej normie. | ||
| Linia 913: | Linia 913: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
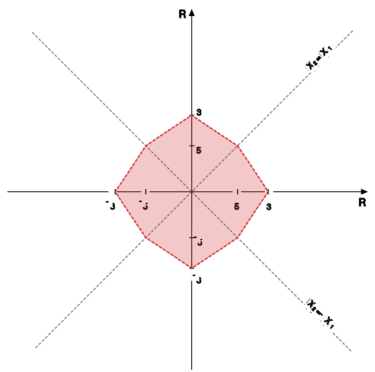
[[File:AM2.M03.C_R05.svg|375x375px|thumb|right|Kula w metryce z ćwiczenia 3.6.]] | [[File:AM2.M03.C_R05.svg|375x375px|thumb|right|Kula w metryce z ćwiczenia 3.6.]] | ||
Niech <math>x\in\mathbb{R}^N | Niech <math>x\in\mathbb{R}^N</math>. | ||
Pokażemy, że | Pokażemy, że | ||
<math>\|x\|_{\square}=0\Longleftrightarrow x=\Theta | <math>\|x\|_{\square}=0\Longleftrightarrow x=\Theta</math>. | ||
Implikacja "<math>\Longleftarrow</math>" jest oczywista. | Implikacja "<math>\Longleftarrow</math>" jest oczywista. | ||
W celu udowodnienia implikacji | W celu udowodnienia implikacji | ||
"<math>\Longrightarrow</math>" załóżmy, że | "<math>\Longrightarrow</math>" załóżmy, że | ||
<math>\|x\|_{\square}=0 | <math>\|x\|_{\square}=0</math>. | ||
Wówczas | Wówczas | ||
<math>2\|x\|_1+\|x\|_{\infty}=0,</math> czyli | <math>2\|x\|_1+\|x\|_{\infty}=0,</math> czyli | ||
<math>\|x\|_1=0</math> i <math>\|x\|_{\infty}=0 | <math>\|x\|_1=0</math> i <math>\|x\|_{\infty}=0</math>. | ||
Ponieważ <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> | Ponieważ <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> | ||
są normami, więc <math>x=\Theta | są normami, więc <math>x=\Theta</math>. | ||
W celu pokazania jednorodności niech | W celu pokazania jednorodności niech | ||
<math>x\in \mathbb{R}^N</math> oraz <math>\lambda\in\mathbb{R} | <math>x\in \mathbb{R}^N</math> oraz <math>\lambda\in\mathbb{R}</math>. | ||
Wówczas | Wówczas | ||
| Linia 952: | Linia 952: | ||
W celu pokazania subaddytywności, | W celu pokazania subaddytywności, | ||
niech <math>x,y\in\mathbb{R}^N | niech <math>x,y\in\mathbb{R}^N</math>. | ||
Wówczas | Wówczas | ||
| Linia 975: | Linia 975: | ||
Co kończy dowód, że <math>\|\cdot\|_{\square}</math> jest norma w | Co kończy dowód, że <math>\|\cdot\|_{\square}</math> jest norma w | ||
<math>\mathbb{R}^N | <math>\mathbb{R}^N</math>.<br> | ||
Aby narysować kulę | Aby narysować kulę | ||
| Linia 1004: | Linia 1004: | ||
Niech <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> oznaczają odpowiednio | Niech <math>\|\cdot\|_1</math> i <math>\|\cdot\|_{\infty}</math> oznaczają odpowiednio | ||
normę taksówkową i maksimową w <math>\mathbb{R}^N | normę taksówkową i maksimową w <math>\mathbb{R}^N</math>. | ||
Sprawdzić, czy | Sprawdzić, czy | ||
| Linia 1012: | Linia 1012: | ||
</math></center> | </math></center> | ||
jest normą w <math>\mathbb{R}^2 | jest normą w <math>\mathbb{R}^2</math>. | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Pokazać brak subaddytywności dla <math>\|\cdot\|_{\circ} | Pokazać brak subaddytywności dla <math>\|\cdot\|_{\circ}</math>. | ||
</div></div> | </div></div> | ||
| Linia 1046: | Linia 1046: | ||
Zatem | Zatem | ||
<math>\|x+y\|_{\circ}\not\le\|x\|_{\circ}+\|y\|_{\circ} | <math>\|x+y\|_{\circ}\not\le\|x\|_{\circ}+\|y\|_{\circ}</math>. | ||
Jako ciekawostkę proponujemy sprawdzenie, że dwa pierwsze | Jako ciekawostkę proponujemy sprawdzenie, że dwa pierwsze | ||
warunki w definicji normy zachodzą dla | warunki w definicji normy zachodzą dla | ||
<math>\|\cdot\|_{\circ} | <math>\|\cdot\|_{\circ}</math>. | ||
</div></div> | </div></div> | ||
| Linia 1065: | Linia 1065: | ||
'''(1)''' | '''(1)''' | ||
Pokazać, że <math>\big(\cdot |\cdot \big)_{\triangle}</math> jest | Pokazać, że <math>\big(\cdot |\cdot \big)_{\triangle}</math> jest | ||
iloczynem skalarnym w <math>\mathbb{R}^2 | iloczynem skalarnym w <math>\mathbb{R}^2</math>.<br> | ||
'''(2)''' | '''(2)''' | ||
Jak wygląda <math>\|\cdot\|_{\triangle}</math> | Jak wygląda <math>\|\cdot\|_{\triangle}</math> | ||
norma zadana przez ten iloczyn skalarny? | norma zadana przez ten iloczyn skalarny? | ||
Obliczyć <math>\|(4,5)\|_{\triangle} | Obliczyć <math>\|(4,5)\|_{\triangle}</math>.<br> | ||
'''(3)''' | '''(3)''' | ||
Dane są dwa wektory | Dane są dwa wektory | ||
<math>x=(1,7)</math> i <math>y=(3,a) | <math>x=(1,7)</math> i <math>y=(3,a)</math>. | ||
Dobrać parametr <math>a\in\mathbb{R}</math> tak, aby | Dobrać parametr <math>a\in\mathbb{R}</math> tak, aby | ||
<math>x\perp y</math> (oczywiście w rozważanym iloczynie skalarnym).<br> | <math>x\perp y</math> (oczywiście w rozważanym iloczynie skalarnym).<br> | ||
| Linia 1122: | Linia 1122: | ||
pokazaliśmy więc punkt (1) definicji iloczynu skalarnego. | pokazaliśmy więc punkt (1) definicji iloczynu skalarnego. | ||
Niech <math>x=(x_1,x_2),y=(y_1,y_2)\in X</math> oraz <math>\lambda\in \mathbb{R} | Niech <math>x=(x_1,x_2),y=(y_1,y_2)\in X</math> oraz <math>\lambda\in \mathbb{R}</math>. | ||
Wówczas | Wówczas | ||
| Linia 1142: | Linia 1142: | ||
Niech teraz | Niech teraz | ||
<math>x=(x_1,x_2),y=(y_1,y_2),z=(z_1,z_2)\in X | <math>x=(x_1,x_2),y=(y_1,y_2),z=(z_1,z_2)\in X</math>. | ||
Wówczas | Wówczas | ||
| Linia 1163: | Linia 1163: | ||
pokazaliśmy więc punkt (3) definicji iloczynu skalarnego. | pokazaliśmy więc punkt (3) definicji iloczynu skalarnego. | ||
W końcu niech <math>x=(x_1,x_2),y=(y_1,y_2)\in X | W końcu niech <math>x=(x_1,x_2),y=(y_1,y_2)\in X</math>. | ||
Wówczas | Wówczas | ||
| Linia 1178: | Linia 1178: | ||
Kończy to dowód faktu, że | Kończy to dowód faktu, że | ||
<math>(\cdot|\cdot)_{\triangle}</math> jest | <math>(\cdot|\cdot)_{\triangle}</math> jest | ||
iloczynem skalarnym w <math>\mathbb{R}^2 | iloczynem skalarnym w <math>\mathbb{R}^2</math>.<br> | ||
<br> | <br> | ||
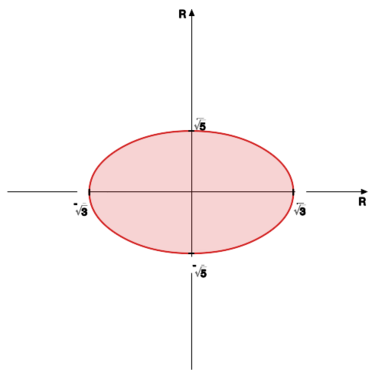
[[File:AM2.M03.C_R06.svg|375x375px|thumb|right|Kula w metryce zadanej przez iloczyn skalarny z ćwiczenia 3.8.]] | [[File:AM2.M03.C_R06.svg|375x375px|thumb|right|Kula w metryce zadanej przez iloczyn skalarny z ćwiczenia 3.8.]] | ||
| Linia 1210: | Linia 1210: | ||
'''(3)''' | '''(3)''' | ||
Wektory <math>x</math> i <math>y</math> są ortogonalne wtedy i tylko wtedy, gdy | Wektory <math>x</math> i <math>y</math> są ortogonalne wtedy i tylko wtedy, gdy | ||
<math>(x|y)_{\triangle}=0 | <math>(x|y)_{\triangle}=0</math>. Zatem musimy rozwiązać równanie | ||
<center> | <center> | ||
| Linia 1229: | Linia 1229: | ||
skąd | skąd | ||
<math>a=-\frac{9}{35} | <math>a=-\frac{9}{35}</math>.<br> | ||
<br> | <br> | ||
'''(4)''' | '''(4)''' | ||
| Linia 1254: | Linia 1254: | ||
spełniających równanie | spełniających równanie | ||
<math>\frac{x_1^2}{a^2}+\frac{x_2^2}{b^2}=1</math> jest elipsą o półosiach | <math>\frac{x_1^2}{a^2}+\frac{x_2^2}{b^2}=1</math> jest elipsą o półosiach | ||
wielkich <math>a</math> i <math>b | wielkich <math>a</math> i <math>b</math>. | ||
Zatem w naszym przypadku | Zatem w naszym przypadku | ||
zbiór punktów <math>(x_1,x_2)\in\mathbb{R}^2</math> spełniających nierówność | zbiór punktów <math>(x_1,x_2)\in\mathbb{R}^2</math> spełniających nierówność | ||
| Linia 1260: | Linia 1260: | ||
jest wnętrzem elipsy o półosiach wielkich | jest wnętrzem elipsy o półosiach wielkich | ||
<math>\frac{1}{\sqrt{3}}</math> | <math>\frac{1}{\sqrt{3}}</math> | ||
oraz <math>\frac{1}{\sqrt{5}} | oraz <math>\frac{1}{\sqrt{5}}</math>.<br> | ||
</div></div> | </div></div> | ||
| Linia 1290: | Linia 1290: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Udowodnić kolejno implikacje | Udowodnić kolejno implikacje | ||
<math>(i)\Longrightarrow(ii)\Longrightarrow(iii)\Longrightarrow(iv)\Longrightarrow(v)\Longrightarrow(vi)\Longrightarrow(i) | <math>(i)\Longrightarrow(ii)\Longrightarrow(iii)\Longrightarrow(iv)\Longrightarrow(v)\Longrightarrow(vi)\Longrightarrow(i)</math>. | ||
</div></div> | </div></div> | ||
| Linia 1300: | Linia 1300: | ||
"<math>(ii)\Longrightarrow(iii)</math>"<br> | "<math>(ii)\Longrightarrow(iii)</math>"<br> | ||
Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | ||
jest ciągła w pewnym punkcie <math>x_0\in X | jest ciągła w pewnym punkcie <math>x_0\in X</math>. | ||
Pokażemy, że jest ciągła w <math>\Theta\in X | Pokażemy, że jest ciągła w <math>\Theta\in X</math>. | ||
Ustalmy dowolne <math>\varepsilon>0 | Ustalmy dowolne <math>\varepsilon>0</math>. | ||
Z definicji Cauchy'ego ciągłości funkcji w punkcie wiemy, że | Z definicji Cauchy'ego ciągłości funkcji w punkcie wiemy, że | ||
| Linia 1314: | Linia 1314: | ||
Dla dowolnego <math>z\in X</math> takiego, że | Dla dowolnego <math>z\in X</math> takiego, że | ||
<math>\|z\|_X\le\delta</math> niech | <math>\|z\|_X\le\delta</math> niech | ||
<math>x=z+x_0 | <math>x=z+x_0</math>. | ||
Wówczas <math>\|x-x_0\|_X=\|z\|_X\le\delta,</math> a zatem korzystając z | Wówczas <math>\|x-x_0\|_X=\|z\|_X\le\delta,</math> a zatem korzystając z | ||
powyższej implikacji, dostajemy, że | powyższej implikacji, dostajemy, że | ||
<math>\|f(z)\|_Y=\|f(x-x_0)\|_Y=\|f(x)-f(x_0)\|_Y\le\varepsilon | <math>\|f(z)\|_Y=\|f(x-x_0)\|_Y=\|f(x)-f(x_0)\|_Y\le\varepsilon</math>. | ||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
| Linia 1326: | Linia 1326: | ||
</math></center> | </math></center> | ||
a to oznacza ciągłość funkcji <math>f</math> w punkcie <math>\Theta | a to oznacza ciągłość funkcji <math>f</math> w punkcie <math>\Theta</math>.<br> | ||
<br> | <br> | ||
"<math>(iii)\Longrightarrow(iv)</math>"<br> | "<math>(iii)\Longrightarrow(iv)</math>"<br> | ||
Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | ||
jest ciągła w punkcie <math>\Theta | jest ciągła w punkcie <math>\Theta</math>. | ||
Ustalmy <math>\varepsilon=1 | Ustalmy <math>\varepsilon=1</math>. | ||
Wówczas | Wówczas | ||
| Linia 1340: | Linia 1340: | ||
</math></center> | </math></center> | ||
Niech <math>M:=\frac{1}{\delta} | Niech <math>M:=\frac{1}{\delta}</math>. | ||
Wówczas dla <math>x\in X\setminus\{\Theta\}</math> takich, że <math>\|x\|_X\le 1</math> | Wówczas dla <math>x\in X\setminus\{\Theta\}</math> takich, że <math>\|x\|_X\le 1</math> | ||
mamy | mamy | ||
| Linia 1385: | Linia 1385: | ||
</math></center> | </math></center> | ||
Niech <math>c:=M | Niech <math>c:=M</math>. | ||
Wówczas dla dowolnego <math>x\in X\setminus\{\Theta\}</math> mamy | Wówczas dla dowolnego <math>x\in X\setminus\{\Theta\}</math> mamy | ||
| Linia 1424: | Linia 1424: | ||
W celu pokazania jednostajnej ciągłości funkcji <math>f</math> | W celu pokazania jednostajnej ciągłości funkcji <math>f</math> | ||
ustalmy dowolne <math>\varepsilon>0 | ustalmy dowolne <math>\varepsilon>0</math>. | ||
Niech | Niech | ||
<math>\delta:=\frac{\varepsilon}{c} | <math>\delta:=\frac{\varepsilon}{c}</math>. | ||
Wówczas dla dowolnych <math>x,z\in X</math> | Wówczas dla dowolnych <math>x,z\in X</math> | ||
takich, że <math>\|x-z\|_X\le\delta,</math> | takich, że <math>\|x-z\|_X\le\delta,</math> | ||
| Linia 1452: | Linia 1452: | ||
</math></center> | </math></center> | ||
co oznacza jednostajną ciągłość funkcji <math>f | co oznacza jednostajną ciągłość funkcji <math>f</math>.<br> | ||
<br> | <br> | ||
"<math>(vi)\Longrightarrow(i)</math>"<br> | "<math>(vi)\Longrightarrow(i)</math>"<br> | ||
Wersja z 09:18, 5 wrz 2023
Norma. Iloczyn skalarny
Ćwiczenie 3.1.
W przestrzeni wektorowej definiujemy:
Pokazać, że oraz są normami (nazywamy je odpowiednio normą euklidesową, normą taksówkową oraz normą maksimową).
Ćwiczenie 3.2.
Pokazać, że norma euklidesowa zadaje metrykę euklidesową, norma taksówkowa zadaje metrykę taksówkową, a norma maksimowa zadaje metrykę maksimową.
Ćwiczenie 3.3.
Wykazać bezpośrednio równoważność norm: (taksówkowej), (euklidesowej) i (maksimowej) w znajdując optymalne stałe () w następujących nierównościach:
Ćwiczenie 3.4.
Niech i będą dwiema przestrzeniami wektorowymi.
Które z poniższych stwierdzeń są prawdziwe?
(Dla każdego podać dowód lub kontrprzykład).
(1)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(2)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(3)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(4)
Jeśli zbiory i
są wypukłe, to zbiór jest wypukły w .
Ćwiczenie 3.5.
W przestrzeni wektorowej funkcji ciągłych na przedziale definiujemy:
(1)
Pokazać, że jest normą
w .
Nazywamy ją normą supremową.
(2)
Obliczyć normę supremową dla funkcji:
oraz
.
(3)
Udowodnić, że zbieżność w normie supremowej pokrywa się ze
zbieżnością jednostajną dla funkcji ciągłych na
przedziale .
(4) Pokazać, że z normą supremową jest przestrzenią Banacha.
(Punkty (3) i (4) są nadobowiązkowe. Potrzebne są tu pewne pojęcia z następnego wykładu. Do zadania można wrócić po następnym wykładzie).
Ćwiczenie 3.6.
Niech i oznaczają odpowiednio normę taksówkową i maksimową w . Pokazać, że
jest normą w . Dla narysować kulę w tej normie.
Ćwiczenie 3.7.
Niech i oznaczają odpowiednio normę taksówkową i maksimową w . Sprawdzić, czy
jest normą w .
Ćwiczenie 3.8.
W wprowadzamy
(1)
Pokazać, że jest
iloczynem skalarnym w .
(2)
Jak wygląda
norma zadana przez ten iloczyn skalarny?
Obliczyć .
(3)
Dane są dwa wektory
i .
Dobrać parametr tak, aby
(oczywiście w rozważanym iloczynie skalarnym).
(4)
Narysować kulę
w metryce zadanej przez ten
iloczyn skalarny.
Ćwiczenie 3.9.
(Zadanie nadobowiązkowe.)
Niech będą dwiema przestrzeniami unormowanymi oraz
odwzorowaniem liniowym.
Udowodnić, że następujące warunki są
równoważne:
(i)
jest ciągła;
(ii)
: jest ciągła w ;
(iii)
jest ciągła w
( oznacza wektor zerowy przestrzeni wektorowej );
(iv)
(to znaczy odwzorowanie jest ograniczone na domkniętej kuli o promieniu );
(v)
(warunek ten nazywa się ograniczonością dla odwzorowania liniowego);
(vi)
jest jednostajnie ciągła.