Analiza matematyczna 2/Ćwiczenia 3: Norma. Iloczyn skalarny: Różnice pomiędzy wersjami
m Zastępowanie tekstu - "<div class="thumb t(.*)"><div style="width:(.*);"> <flash>file=(.*)\.swf\|width=(.*)\|height=(.*)<\/flash> <div\.thumbcaption>(.*)<\/div> <\/div><\/div>" na "$4x$5px|thumb|$1|$6" |
m Zastępowanie tekstu – „\displaystyle ” na „” |
||
| Linia 4: | Linia 4: | ||
W przestrzeni wektorowej | W przestrzeni wektorowej | ||
<math> | <math>\mathbb{R}^N</math> definiujemy: | ||
<center><math> | <center><math>\|x\|_{2} | ||
\stackrel{df}{=} | \stackrel{df}{=} | ||
\sqrt{\sum_{i=1}^N x_i^2}, | \sqrt{\sum_{i=1}^N x_i^2}, | ||
| Linia 16: | Linia 16: | ||
\stackrel{df}{=} | \stackrel{df}{=} | ||
\max_{1\le i\le N} |x_i| | \max_{1\le i\le N} |x_i| | ||
\quad </math> dla <math> | \quad </math> dla <math> \ x\in\mathbb{R}^N. | ||
</math></center> | </math></center> | ||
Pokazać, że | Pokazać, że | ||
<math> | <math>\displaystyle\|\cdot\|_2,\displaystyle\|\cdot\|_1</math> oraz | ||
<math> | <math>\displaystyle\|\cdot\|_{\infty}</math> | ||
są normami | są normami | ||
(nazywamy je odpowiednio normą euklidesową, | (nazywamy je odpowiednio normą euklidesową, | ||
| Linia 29: | Linia 29: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' | '''(1)''' | ||
Pokazać, że <math> | Pokazać, że <math>\displaystyle\|\cdot\|_2</math> jest normą | ||
wprost z definicji normy. | wprost z definicji normy. | ||
Przy dowodzie subaddytywności wykorzystać nierówność | Przy dowodzie subaddytywności wykorzystać nierówność | ||
| Linia 36: | Linia 36: | ||
'''(2)-(3)''' | '''(2)-(3)''' | ||
Pokazać, że | Pokazać, że | ||
<math> | <math>\displaystyle\|\cdot\|_1</math> i <math>\displaystyle\|\cdot\|_{\infty}</math> | ||
są normami, korzystając z definicji normy. | są normami, korzystając z definicji normy. | ||
</div></div> | </div></div> | ||
| Linia 42: | Linia 42: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' | '''(1)''' | ||
Pokażemy, że <math> | Pokażemy, że <math>\displaystyle\|\cdot\|_2</math> jest normą.<br> | ||
Dla <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | ||
<center><math> | <center><math>\|x\|_2=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
\sqrt{\sum_{i=1}^N x_i^2}=0 | \sqrt{\sum_{i=1}^N x_i^2}=0 | ||
| Linia 56: | Linia 56: | ||
</math></center> | </math></center> | ||
Dla <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math>\displaystyle\lambda\in\mathbb{R}</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|\lambda x\|_2 | ||
= | = | ||
\sqrt{\sum_{i=1}^N (\lambda x_i)^2} | \sqrt{\sum_{i=1}^N (\lambda x_i)^2} | ||
| Linia 72: | Linia 72: | ||
zatem pokazaliśmy warunek jednorodności. | zatem pokazaliśmy warunek jednorodności. | ||
W końcu dla dowolnych <math> | W końcu dla dowolnych <math>x,y\in\mathbb{R}^N</math> mamy | ||
<center><math> | <center><math>\|x+y\|_2 | ||
= | = | ||
\sum_{i=1}^N(x_i+y_i)^2 | \sum_{i=1}^N(x_i+y_i)^2 | ||
| Linia 91: | Linia 91: | ||
patrz [[Analiza matematyczna 1/Wykład 3: Odległość i ciągi#lemat_3_8|Analiza matematyczna 1 lemat 3.8.]]) | patrz [[Analiza matematyczna 1/Wykład 3: Odległość i ciągi#lemat_3_8|Analiza matematyczna 1 lemat 3.8.]]) | ||
<center><math> | <center><math>\forall x,y\in\mathbb{R}^N: | ||
\bigg( | \bigg(\sum_{i=1}^N x_iy_i\bigg)^2 | ||
\le | \le | ||
\bigg( | \bigg(\sum_{i=1}^N x_i^2\bigg) | ||
\bigg( | \bigg(\sum_{i=1}^N y_i^2\bigg), | ||
</math></center> | </math></center> | ||
| Linia 102: | Linia 102: | ||
<center><math> | <center><math> | ||
\begin{array}{lll} | \begin{array}{lll} | ||
\|x+y\|_2^2\ &\le& | |||
\sum_{i=1}^Nx_i^2+ | \sum_{i=1}^Nx_i^2+ | ||
2\bigg( | 2\bigg(\sum_{i=1}^N x_i^2\bigg) | ||
\bigg( | \bigg(\sum_{i=1}^N y_i^2\bigg) | ||
+\sum_{i=1}^Ny_i^2\\ | +\sum_{i=1}^Ny_i^2\\ | ||
&=& | &=& | ||
\bigg(\sum_{i=1}^Nx_i^2+\sum_{i=1}^Ny_i^2\bigg) | \bigg(\sum_{i=1}^Nx_i^2+\sum_{i=1}^Ny_i^2\bigg) | ||
= | = | ||
| Linia 115: | Linia 115: | ||
zatem pokazaliśmy warunek subaddytywności: | zatem pokazaliśmy warunek subaddytywności: | ||
<center><math> | <center><math>\forall x,y\in\mathbb{R}^N: | ||
\|x+y\|_2 | \|x+y\|_2 | ||
\le | \le | ||
| Linia 124: | Linia 124: | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
Pokażemy, że <math> | Pokażemy, że <math>\displaystyle\|\cdot\|_1</math> jest normą.<br> | ||
Dla <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | ||
<center><math> | <center><math>\|x\|_1=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
\sum_{i=1}^N |x_i|=0 | \sum_{i=1}^N |x_i|=0 | ||
| Linia 136: | Linia 136: | ||
</math></center> | </math></center> | ||
Dla <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math>\displaystyle\lambda\in\mathbb{R}</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|\lambda x\|_1 | ||
= | = | ||
\sum_{i=1}^N |\lambda x_i| | \sum_{i=1}^N |\lambda x_i| | ||
| Linia 150: | Linia 150: | ||
zatem pokazaliśmy warunek jednorodności. | zatem pokazaliśmy warunek jednorodności. | ||
W końcu dla dowolnych <math> | W końcu dla dowolnych <math>x,y\in\mathbb{R}^N</math> mamy | ||
<center><math>\begin{array}{lll} | <center><math>\begin{array}{lll} | ||
\|x+y\|_1 | |||
&=& | &=& | ||
\sum_{i=1}^N|x_i+y_i| | \sum_{i=1}^N|x_i+y_i| | ||
\le | \le | ||
\sum_{i=1}^N\big(|x_i|+|y_i|\big)\\ | \sum_{i=1}^N\big(|x_i|+|y_i|\big)\\ | ||
&=& | &=& | ||
\sum_{i=1}^N|x_i| | \sum_{i=1}^N|x_i| | ||
+\sum_{i=1}^N|y_i| | +\sum_{i=1}^N|y_i| | ||
| Linia 169: | Linia 169: | ||
<br> | <br> | ||
'''(3)''' | '''(3)''' | ||
Pokażemy, że <math> | Pokażemy, że <math>\displaystyle\|\cdot\|_{\infty}</math> jest normą.<br> | ||
Dla <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> mamy | ||
<center><math> | <center><math>\|x\|_{\infty}=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
\max_{i=1,\ldots,N} |x_i|=0 | \max_{i=1,\ldots,N} |x_i|=0 | ||
| Linia 181: | Linia 181: | ||
</math></center> | </math></center> | ||
Dla <math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math>\displaystyle\lambda\in\mathbb{R}</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|\lambda x\|_{\infty} | ||
= | = | ||
\max_{i=1,\ldots,N} |\lambda x_i| | \max_{i=1,\ldots,N} |\lambda x_i| | ||
| Linia 195: | Linia 195: | ||
zatem pokazaliśmy warunek jednorodności. | zatem pokazaliśmy warunek jednorodności. | ||
W końcu dla dowolnych <math> | W końcu dla dowolnych <math>x,y\in\mathbb{R}^N</math> mamy | ||
<center><math> | <center><math> | ||
\begin{array}{lll} | \begin{array}{lll} | ||
\|x+y\|_{\infty}& =& | |||
\max_{i=1,\ldots,N} |x_i+y_i| | \max_{i=1,\ldots,N} |x_i+y_i| | ||
\le | \le | ||
\max_{i=1,\ldots,N}\big(|x_i|+|y_i|\big)\\\\ | \max_{i=1,\ldots,N}\big(|x_i|+|y_i|\big)\\\\ | ||
&\le & | &\le & | ||
\max_{i=1,\ldots,N}|x_i| | \max_{i=1,\ldots,N}|x_i| | ||
+\max_{i=1,\ldots,N}|y_i| | +\max_{i=1,\ldots,N}|y_i| | ||
| Linia 228: | Linia 228: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Dla dowolnych <math> | Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | ||
<center><math> | <center><math>\|x-y\|_2 | ||
= | = | ||
\sqrt{\sum_{i=1}^N(x_i-y_i)^2} | \sqrt{\sum_{i=1}^N(x_i-y_i)^2} | ||
| Linia 237: | Linia 237: | ||
</math></center> | </math></center> | ||
więc norma euklidesowa <math> | więc norma euklidesowa <math>\displaystyle\|\cdot\|_2</math> zadaje metrykę euklidesową | ||
<math> | <math>d_2.</math> | ||
Dla dowolnych <math> | Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | ||
<center><math> | <center><math>\|x-y\|_1 | ||
= | = | ||
\sum_{i=1}^N|x_i-y_i| | \sum_{i=1}^N|x_i-y_i| | ||
| Linia 249: | Linia 249: | ||
</math></center> | </math></center> | ||
więc norma taksówkowa <math> | więc norma taksówkowa <math>\displaystyle\|\cdot\|_1</math> zadaje metrykę taksówkową | ||
<math> | <math>d_2.</math> | ||
Dla dowolnych <math> | Dla dowolnych <math>x,y\in\mathbb{R}</math> zauważmy, że | ||
<center><math> | <center><math>\|x-y\|_{\infty} | ||
= | = | ||
\max_{i=1,\ldots,N}|x_i-y_i| | \max_{i=1,\ldots,N}|x_i-y_i| | ||
| Linia 260: | Linia 260: | ||
</math></center> | </math></center> | ||
więc norma maksimowa <math> | więc norma maksimowa <math>\displaystyle\|\cdot\|_{\infty}</math> zadaje metrykę maksimową | ||
<math> | <math>d_{\infty}.</math> | ||
</div></div> | </div></div> | ||
| Linia 267: | Linia 267: | ||
Wykazać bezpośrednio równoważność norm: | Wykazać bezpośrednio równoważność norm: | ||
<math> | <math>\displaystyle\|\cdot\|_1</math> (taksówkowej), | ||
<math> | <math>\displaystyle\|\cdot\|_2</math> (euklidesowej) | ||
i <math> | i <math>\displaystyle\|\cdot\|_{\infty}</math> (maksimowej) | ||
w <math> | w <math>\displaystyle\mathbb{R}^N,</math> znajdując optymalne | ||
stałe <math> | stałe <math>m_i,M_i>0</math> (<math>i=1,2,3</math>) | ||
w następujących nierównościach: | w następujących nierównościach: | ||
<center><math> | <center><math>\begin{align} | ||
\textbf{(1)} && | \textbf{(1)} && | ||
\forall x\in \mathbb{R}^N: | \forall x\in \mathbb{R}^N: | ||
| Linia 302: | Linia 302: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' Skorzystać jedynie z definicji norm | '''(1)''' Skorzystać jedynie z definicji norm | ||
<math> | <math>\displaystyle\|\cdot\|_2</math> i <math>\displaystyle\|\cdot\|_{\infty},</math> | ||
dla pokazania nierówności i wyznaczenia stałych. | dla pokazania nierówności i wyznaczenia stałych. | ||
Aby pokazać "optymalność" stałych, | Aby pokazać "optymalność" stałych, | ||
wskazać wektor <math> | wskazać wektor <math>x_0\in\mathbb{R}^N,</math> dla którego zachodzą równości.<br> | ||
<br> | <br> | ||
'''(2)-(3)''' Podobnie jak (1). | '''(2)-(3)''' Podobnie jak (1). | ||
| Linia 312: | Linia 312: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' | '''(1)''' | ||
Dla dowolnego wektora <math> | Dla dowolnego wektora <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|x\|_2^2 | ||
= | = | ||
\sum_{i=1}^N |x_i|^2 | \sum_{i=1}^N |x_i|^2 | ||
| Linia 328: | Linia 328: | ||
Zatem | Zatem | ||
<center><math> | <center><math>\forall x\in \mathbb{R}^N: | ||
\frac{1}{\sqrt{N}}\|x\|_2 | \frac{1}{\sqrt{N}}\|x\|_2 | ||
\le | \le | ||
| Linia 335: | Linia 335: | ||
czyli | czyli | ||
<math> | <math>m_1=\frac{1}{\sqrt{N}}.</math> | ||
Aby pokazać, że stała <math> | Aby pokazać, że stała <math>m_1</math> jest "optymalna" | ||
(to znaczy największa z możliwych), zauważmy, że dla wektora | (to znaczy największa z możliwych), zauważmy, że dla wektora | ||
<math> | <math>x_0=(1,1,\ldots,1)</math> mamy | ||
<center><math> | <center><math>\frac{1}{\sqrt{N}}\|x_0\|_2 | ||
= | = | ||
\frac{1}{\sqrt{N}}\sqrt{N} | \frac{1}{\sqrt{N}}\sqrt{N} | ||
| Linia 349: | Linia 349: | ||
</math></center> | </math></center> | ||
Z kolei dla dowolnego wektora <math> | Z kolei dla dowolnego wektora <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|x\|_{\infty}^2 | ||
= | = | ||
\bigg(\max_{i=1,\ldots, N}|x_i|\bigg)^2 | \bigg(\max_{i=1,\ldots, N}|x_i|\bigg)^2 | ||
| Linia 365: | Linia 365: | ||
Zatem | Zatem | ||
<center><math> | <center><math>\forall x\in \mathbb{R}^N: | ||
\|x\|_{\infty} | \|x\|_{\infty} | ||
\le | \le | ||
| Linia 371: | Linia 371: | ||
</math></center> | </math></center> | ||
czyli <math> | czyli <math>M_1=1.</math> Aby pokazać, że stała <math>M_1</math> jest "optymalna" | ||
(to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | (to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | ||
<math> | <math>x_0=(1,0,\ldots,0)</math> mamy | ||
<center><math> | <center><math>\|x_0\|_{\infty} | ||
= | = | ||
1 | 1 | ||
| Linia 383: | Linia 383: | ||
'''(2)''' | '''(2)''' | ||
Dla dowolnego wektora <math> | Dla dowolnego wektora <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|x\|_1 | ||
= | = | ||
\sum_{i=1}^N |x_i| | \sum_{i=1}^N |x_i| | ||
| Linia 399: | Linia 399: | ||
Zatem | Zatem | ||
<center><math> | <center><math>\forall x\in \mathbb{R}^N: | ||
\frac{1}{N}\|x\|_1 | \frac{1}{N}\|x\|_1 | ||
\le | \le | ||
| Linia 406: | Linia 406: | ||
czyli | czyli | ||
<math> | <math>m_2=\frac{1}{N}.</math> | ||
Aby pokazać, że stała <math> | Aby pokazać, że stała <math>m_2</math> jest "optymalna" | ||
(to znaczy największa z możliwych), zauważmy, że dla wektora | (to znaczy największa z możliwych), zauważmy, że dla wektora | ||
<math> | <math>x_0=(1,1,\ldots,1)</math> mamy | ||
<center><math> | <center><math>\frac{1}{N}\|x_0\|_1 | ||
= | = | ||
\frac{1}{N}\cdot N | \frac{1}{N}\cdot N | ||
| Linia 420: | Linia 420: | ||
</math></center> | </math></center> | ||
Z kolei dla dowolnego wektora <math> | Z kolei dla dowolnego wektora <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|x\|_{\infty} | ||
= | = | ||
\max_{i=1,\ldots, N}|x_i| | \max_{i=1,\ldots, N}|x_i| | ||
| Linia 434: | Linia 434: | ||
Zatem | Zatem | ||
<center><math> | <center><math>\forall x\in \mathbb{R}^N: | ||
\|x\|_{\infty} | \|x\|_{\infty} | ||
\le | \le | ||
| Linia 440: | Linia 440: | ||
</math></center> | </math></center> | ||
czyli <math> | czyli <math>M_1=1.</math> Aby pokazać, że stała <math>M_1</math> jest "optymalna" | ||
(to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | (to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | ||
<math> | <math>x_0=(1,0,\ldots,0)</math> mamy | ||
<center><math> | <center><math>\|x_0\|_{\infty} | ||
= | = | ||
1 | 1 | ||
| Linia 452: | Linia 452: | ||
'''(3)''' | '''(3)''' | ||
Dla dowolnego wektora <math> | Dla dowolnego wektora <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|x\|_1^2 | ||
= | = | ||
\bigg(\sum_{i=1}^N |x_i|\bigg)^2 | \bigg(\sum_{i=1}^N |x_i|\bigg)^2 | ||
| Linia 467: | Linia 467: | ||
Korzystając teraz z oczywistej nierówności liczbowej | Korzystając teraz z oczywistej nierówności liczbowej | ||
<center><math> | <center><math>\forall a,b\in\mathbb{R}: | ||
2ab | 2ab | ||
\le | \le | ||
| Linia 475: | Linia 475: | ||
mamy | mamy | ||
<center><math> | <center><math>\|x\|_1^2 | ||
\le | \le | ||
\sum_{i}^N|x_i|^2 | \sum_{i}^N|x_i|^2 | ||
| Linia 482: | Linia 482: | ||
Zauważmy, że po prawej stronie powyższej nierówności każdy | Zauważmy, że po prawej stronie powyższej nierówności każdy | ||
składnik postaci <math> | składnik postaci <math>|x_i|^2</math> występuje dokładnie <math>N</math> razy | ||
(raz w pierwszej sumie i <math> | (raz w pierwszej sumie i <math>N-1</math> razy w drugiej sumie). | ||
Zatem | Zatem | ||
<center><math> | <center><math>\|x\|_1^2 | ||
\le | \le | ||
N \sum_{i=1}^N|x_i|^2 | N \sum_{i=1}^N|x_i|^2 | ||
| Linia 495: | Linia 495: | ||
Zatem | Zatem | ||
<center><math> | <center><math>\forall x\in \mathbb{R}^N: | ||
\frac{1}{\sqrt{N}}\|x\|_1 | \frac{1}{\sqrt{N}}\|x\|_1 | ||
\le | \le | ||
| Linia 502: | Linia 502: | ||
czyli | czyli | ||
<math> | <math>m_3=\frac{1}{\sqrt{N}}.</math> | ||
Aby pokazać, że stała <math> | Aby pokazać, że stała <math>m_3</math> jest "optymalna" | ||
(to znaczy największa z możliwych), zauważmy, że dla wektora | (to znaczy największa z możliwych), zauważmy, że dla wektora | ||
<math> | <math>x_0=(1,1,\ldots,1)</math> mamy | ||
<center><math> | <center><math>\frac{1}{\sqrt{N}}\|x_0\|_1 | ||
= | = | ||
\frac{1}{\sqrt{N}}\cdot N | \frac{1}{\sqrt{N}}\cdot N | ||
| Linia 516: | Linia 516: | ||
</math></center> | </math></center> | ||
Z kolei dla dowolnego wektora <math> | Z kolei dla dowolnego wektora <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|x\|_2 | ||
= | = | ||
\sum_{i=1}^N |x_i|^2 | \sum_{i=1}^N |x_i|^2 | ||
| Linia 530: | Linia 530: | ||
Zatem | Zatem | ||
<center><math> | <center><math>\forall x\in \mathbb{R}^N: | ||
\|x\|_2 | \|x\|_2 | ||
\le | \le | ||
| Linia 536: | Linia 536: | ||
</math></center> | </math></center> | ||
czyli <math> | czyli <math>M_3=1.</math> Aby pokazać, że stała <math>M_3</math> jest "optymalna" | ||
(to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | (to znaczy najmniejsza z możliwych), zauważmy, że dla wektora | ||
<math> | <math>x_0=(1,0,\ldots,0)</math> mamy | ||
<center><math> | <center><math>\|x_0\|_2 | ||
= | = | ||
1 | 1 | ||
| Linia 551: | Linia 551: | ||
<span id="cw_3_4">{{cwiczenie|3.4.|| | <span id="cw_3_4">{{cwiczenie|3.4.|| | ||
Niech <math> | Niech <math>X</math> i <math>Y</math> będą dwiema przestrzeniami wektorowymi. | ||
Które z poniższych stwierdzeń są prawdziwe? | Które z poniższych stwierdzeń są prawdziwe? | ||
(Dla każdego podać dowód lub kontrprzykład).<br> | (Dla każdego podać dowód lub kontrprzykład).<br> | ||
'''(1)''' | '''(1)''' | ||
Jeśli zbiory <math> | Jeśli zbiory <math>A,B\subseteq X</math> są wypukłe, to zbiór <math>A\cap B</math> jest wypukły.<br> | ||
'''(2)''' | '''(2)''' | ||
Jeśli zbiory <math> | Jeśli zbiory <math>A,B\subseteq X</math> są wypukłe, to zbiór <math>A\cup B</math> jest wypukły.<br> | ||
'''(3)''' | '''(3)''' | ||
Jeśli zbiory <math> | Jeśli zbiory <math>A,B\subseteq X</math> są wypukłe, to zbiór <math>A\setminus B</math> jest wypukły.<br> | ||
'''(4)''' | '''(4)''' | ||
Jeśli zbiory <math> | Jeśli zbiory <math>A\subseteq X</math> i <math>B\subseteq Y</math> | ||
są wypukłe, to zbiór <math> | są wypukłe, to zbiór <math>A\times B</math> jest wypukły w <math>X\times Y.</math><br> | ||
}}</span> | }}</span> | ||
| Linia 584: | Linia 584: | ||
'''(1)''' | '''(1)''' | ||
Stwierdzenie to jest prawdziwe. | Stwierdzenie to jest prawdziwe. | ||
Niech <math> | Niech <math>A,B\subseteq X</math> będą dowolnymi zbiorami wypukłymi. | ||
Aby pokazać, że zbiór <math> | Aby pokazać, że zbiór <math>A\cap B</math> jest wypukły, | ||
wybierzmy dwa dowolne punkty | wybierzmy dwa dowolne punkty | ||
<math> | <math>x,y\in A\cap B</math> oraz <math>\displaystyle\lambda\in(0,1).</math> | ||
Ponieważ | Ponieważ | ||
<math> | <math>x,y\in A</math> i zbiór <math>A</math> jest wypukły, | ||
więc także | więc także | ||
<math> | <math>\displaystyle\lambda x+(1-\lambda)y\in A.</math> | ||
Analogicznie ponieważ | Analogicznie ponieważ | ||
<math> | <math>x,y\in B</math> i zbiór <math>B</math> jest wypukły, | ||
więc także | więc także | ||
<math> | <math>\displaystyle\lambda x+(1-\lambda)y\in B.</math> | ||
Zatem | Zatem | ||
<math> | <math>\displaystyle\lambda x+(1-\lambda)y\in A\cap B.</math> | ||
Dowodzi to wypukłości zbioru <math> | Dowodzi to wypukłości zbioru <math>A\cap B.</math><br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
Stwierdzenie to nie jest prawdziwe. | Stwierdzenie to nie jest prawdziwe. | ||
Dla przykładu niech | Dla przykładu niech | ||
<math> | <math>X=\mathbb{R},A=[0,2]</math> oraz <math>B=[4,6].</math> | ||
Zbiory <math> | Zbiory <math>A</math> i <math>B</math> są wypukłe, ale | ||
zbiór <math> | zbiór <math>A\cup B=[0,2]\cup [4,6]</math> nie jest wypukły, | ||
gdyż na przykład dla <math> | gdyż na przykład dla <math>x=1,y=5</math> i <math>\displaystyle\lambda=\frac{1}{2}</math> | ||
mamy <math> | mamy <math>x,y\in A\cup B,\displaystyle\lambda\in(0,1),</math> | ||
ale <math> | ale <math>\displaystyle\lambda x+(1-\lambda)y=3\not\in A\cup B.</math><br> | ||
<br> | <br> | ||
'''(3)''' | '''(3)''' | ||
Stwierdzenie to nie jest prawdziwe. | Stwierdzenie to nie jest prawdziwe. | ||
Dla przykładu niech | Dla przykładu niech | ||
<math> | <math>X=\mathbb{R},A=[0,6]</math> oraz <math>B=(2,4).</math> | ||
Zbiory <math> | Zbiory <math>A</math> i <math>B</math> są wypukłe, ale | ||
zbiór <math> | zbiór <math>A\cup B=[0,2]\cup [4,6]</math> nie jest wypukły | ||
(patrz (2)). | (patrz (2)). | ||
| Linia 621: | Linia 621: | ||
'''(4)''' | '''(4)''' | ||
Stwierdzenie to jest prawdziwe. | Stwierdzenie to jest prawdziwe. | ||
Niech <math> | Niech <math>A\subseteq X</math> i <math>B\subseteq Y</math> | ||
będą dowolnymi zbiorami wypukłymi. | będą dowolnymi zbiorami wypukłymi. | ||
Aby pokazać, że zbiór <math> | Aby pokazać, że zbiór <math>A\times B</math> jest wypukły, | ||
wybierzmy dwa dowolne punkty | wybierzmy dwa dowolne punkty | ||
<math> | <math>(a_1,b_1),(a_2,b_2)\in A\times B</math> oraz <math>\displaystyle\lambda\in(0,1).</math> | ||
Wówczas | Wówczas | ||
<center> | <center> | ||
<math> | <math>\lambda(a_1,b_1)+(1-\lambda)(a_2,b_2) | ||
= | = | ||
\big(\lambda a_1+(1-\lambda)a_2,\lambda b_1+(1-\lambda)b_2\big). | \big(\lambda a_1+(1-\lambda)a_2,\lambda b_1+(1-\lambda)b_2\big). | ||
| Linia 635: | Linia 635: | ||
</center> | </center> | ||
Ponieważ zbiory <math> | Ponieważ zbiory <math>A</math> i <math>B</math> są wypukłe odpowiednio w | ||
przestrzeniach <math> | przestrzeniach <math>X</math> i <math>Y,</math> zatem mamy | ||
<center> | <center> | ||
<math> | <math>\lambda a_1+(1-\lambda)a_2\ \in\ A,\quad | ||
\lambda b_1+(1-\lambda)b_2\ \in\ B. | \lambda b_1+(1-\lambda)b_2\ \in\ B. | ||
</math> | </math> | ||
| Linia 647: | Linia 647: | ||
<center> | <center> | ||
<math> | <math>\big(\lambda a_1+(1-\lambda)a_2,\lambda b_1+(1-\lambda)b_2\big) | ||
\ \in | \ \in | ||
A\times B. | A\times B. | ||
| Linia 653: | Linia 653: | ||
</center> | </center> | ||
Zatem pokazaliśmy, że zbiór <math> | Zatem pokazaliśmy, że zbiór <math>A\times B</math> | ||
jest wypukły. | jest wypukły. | ||
</div></div> | </div></div> | ||
| Linia 660: | Linia 660: | ||
W przestrzeni wektorowej | W przestrzeni wektorowej | ||
<math> | <math>C\big([0,1];\mathbb{R}\big),</math> funkcji ciągłych na przedziale <math>[0,1]</math> | ||
definiujemy: | definiujemy: | ||
<center> | <center> | ||
<math> | <math>\|f\|_{\infty} | ||
= | = | ||
\sup_{x\in[0,1]}|f(x)| | \sup_{x\in[0,1]}|f(x)| | ||
| Linia 672: | Linia 672: | ||
'''(1)''' | '''(1)''' | ||
Pokazać, że <math> | Pokazać, że <math>\displaystyle\|\cdot\|_{\infty}</math> jest normą | ||
w <math> | w <math>C\big([0,1];\mathbb{R}\big).</math> | ||
Nazywamy ją '''''normą supremową'''''.<br> | Nazywamy ją '''''normą supremową'''''.<br> | ||
'''(2)''' | '''(2)''' | ||
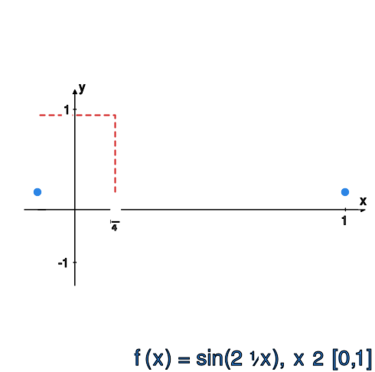
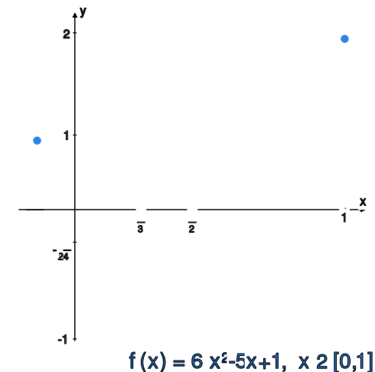
Obliczyć normę supremową dla funkcji: | Obliczyć normę supremową dla funkcji: | ||
<math> | <math>f_1(x)=\sin(2\pi x)</math> oraz | ||
<math> | <math>f_2(x)=6x^2-5x+1.</math><br> | ||
'''(3)''' | '''(3)''' | ||
Udowodnić, że zbieżność w normie supremowej pokrywa się ze | Udowodnić, że zbieżność w normie supremowej pokrywa się ze | ||
zbieżnością jednostajną dla funkcji ciągłych na | zbieżnością jednostajną dla funkcji ciągłych na | ||
przedziale <math> | przedziale <math>[0,1].</math><br> | ||
'''(4)''' | '''(4)''' | ||
Pokazać, że <math> | Pokazać, że <math>C\big([0,1];\mathbb{R}\big)</math> z normą | ||
supremową jest przestrzenią Banacha. | supremową jest przestrzenią Banacha. | ||
| Linia 699: | Linia 699: | ||
definicji normy.<br> | definicji normy.<br> | ||
'''(2)''' Wyznaczyć największą wartość funkcji | '''(2)''' Wyznaczyć największą wartość funkcji | ||
<math> | <math>|f_1|</math> i <math>|f_2|</math> na przedziale <math>[0,1].</math><br> | ||
'''(3)''' Wynika wprost z obu rozważanych definicji.<br> | '''(3)''' Wynika wprost z obu rozważanych definicji.<br> | ||
'''(4)''' Wykorzystać punkt (3) i twierdzenie | '''(4)''' Wykorzystać punkt (3) i twierdzenie | ||
| Linia 711: | Linia 711: | ||
Pokażemy, że | Pokażemy, że | ||
<center><math> | <center><math>\|f\|_{\infty}=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
f\equiv 0. | f\equiv 0. | ||
</math></center> | </math></center> | ||
Implikacja "<math> | Implikacja "<math>\displaystyle\Longrightarrow</math>" jest oczywista. | ||
W celu udowodnienia implikacji | W celu udowodnienia implikacji | ||
"<math> | "<math>\displaystyle\Longleftarrow</math>" załóżmy, że | ||
<math> | <math>\displaystyle\|f\|_{\infty}=0.</math> | ||
Wówczas | Wówczas | ||
<math> | <math>\displaystyle\sup_{x\in [0,1]}|f(x)|=0.</math> | ||
To oznacza, że | To oznacza, że | ||
<math> | <math>|f(x)|=0</math> dla każdego <math>x\in [0,1],</math> czyli | ||
<math> | <math>f(x)=0</math> dla każdego <math>x\in [0,1],</math> | ||
zatem | zatem | ||
<math> | <math>f\equiv 0,</math> co należało pokazać. | ||
W celu pokazania jednorodności, niech | W celu pokazania jednorodności, niech | ||
<math> | <math>f\in C\big([0,1];\mathbb{R}\big)</math> | ||
oraz <math> | oraz <math>\displaystyle\lambda\in \mathbb{R}.</math> | ||
Wówczas | Wówczas | ||
<center><math> | <center><math> | ||
\begin{array}{lll} | \begin{array}{lll} | ||
\|f\lambda f\|_{\infty} | |||
&=& | &=& | ||
\sup_{x\in [0,1]}|\lambda f(x)| | \sup_{x\in [0,1]}|\lambda f(x)| | ||
= | = | ||
\sup_{x\in [0,1]}|\lambda| |f(x)|\\ | \sup_{x\in [0,1]}|\lambda| |f(x)|\\ | ||
&=& | &=& | ||
|\lambda|\sup_{x\in [0,1]}|f(x)| | |\lambda|\sup_{x\in [0,1]}|f(x)| | ||
= | = | ||
| Linia 750: | Linia 750: | ||
Aby pokazać subaddytywność, niech | Aby pokazać subaddytywność, niech | ||
<math> | <math>f,g\in C\big([0,1];\mathbb{R}\big).</math> | ||
Wówczas | Wówczas | ||
<center><math> | <center><math> | ||
\begin{array}{lll} | \begin{array}{lll} | ||
\|f+g\|_{\infty} | \|f+g\|_{\infty} | ||
&=& | &=& \sup_{x\in [0,1]}\big|(f+g)(x)\big| | ||
= | = | ||
\sup_{x\in [0,1]}\big|f(x)+g(x)\big| | \sup_{x\in [0,1]}\big|f(x)+g(x)\big| | ||
\le | \le | ||
\sup_{x\in [0,1]}\big[\big|f(x)\big|+\big|g(x)\big|\big]\\ | \sup_{x\in [0,1]}\big[\big|f(x)\big|+\big|g(x)\big|\big]\\ | ||
& \stackrel{\star}{\le} & | & \stackrel{\star}{\le} & | ||
\sup_{x\in [0,1]}\big|f(x)\big| | \sup_{x\in [0,1]}\big|f(x)\big| | ||
+\sup_{x\in [0,1]}\big|g(x)\big| | +\sup_{x\in [0,1]}\big|g(x)\big| | ||
| Linia 768: | Linia 768: | ||
\end{array}</math></center> | \end{array}</math></center> | ||
Aby uzasadnić powyższą nierówność <math> | Aby uzasadnić powyższą nierówność <math>\displaystyle\star,</math> | ||
zauważmy, że | zauważmy, że | ||
<center><math> | <center><math>\forall x\in [0,1]: | ||
\big|f(x)\big|+\big|g(x)\big| | \big|f(x)\big|+\big|g(x)\big| | ||
\le | \le | ||
| Linia 780: | Linia 780: | ||
zatem biorąc supremum po lewej, stronie nierówność nadal jest | zatem biorąc supremum po lewej, stronie nierówność nadal jest | ||
zachowana i dostajemy <math> | zachowana i dostajemy <math>\displaystyle\star.</math><br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
Ponieważ | Ponieważ | ||
<math> | <math>f_1\bigg(\frac{1}{4}\bigg)=\sin\frac{\pi}{2}=1</math> | ||
oraz <math> | oraz <math>|f_1(x)|=|\sin(2\pi x)|\le 1</math> dla dowolnego | ||
<math> | <math>x\in [0,1],</math> zatem | ||
<math> | <math>\displaystyle\|f_1\|_{\infty}=1.</math><br> | ||
Funkcja kwadratowa na odcinku domkniętym może przyjmować wartość | Funkcja kwadratowa na odcinku domkniętym może przyjmować wartość | ||
| Linia 793: | Linia 793: | ||
przedziału. Należy zatem zbadać te trzy punkty.<br> | przedziału. Należy zatem zbadać te trzy punkty.<br> | ||
Wierzchołek paraboli ma współrzędne | Wierzchołek paraboli ma współrzędne | ||
<math> | <math>(p,q)=\bigg(\frac{-b}{2a},\frac{-\Delta}{4a}\bigg) | ||
=\bigg(\frac{5}{12},-\frac{1}{24}\bigg).</math> | =\bigg(\frac{5}{12},-\frac{1}{24}\bigg).</math> | ||
Na końcach przedziału mamy wartości | Na końcach przedziału mamy wartości | ||
<math> | <math>f_2(0)=1,f_2(1)=2,</math> zatem | ||
<center><math> | <center><math>\|f_2\|_{\infty} | ||
= | = | ||
\max\bigg\{\bigg|-\frac{1}{24}\bigg|,|1|,|2|\bigg\} | \max\bigg\{\bigg|-\frac{1}{24}\bigg|,|1|,|2|\bigg\} | ||
| Linia 812: | Linia 812: | ||
'''(3)''' | '''(3)''' | ||
Zbieżność | Zbieżność | ||
<math> | <math>f_n\xrightarrow{\|\cdot\|_{\infty}} f</math> oznacza | ||
z definicji: | z definicji: | ||
<center><math> | <center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N: | ||
\|f_n-f\|_{\infty}<\varepsilon. | \|f_n-f\|_{\infty}<\varepsilon. | ||
</math></center> | </math></center> | ||
| Linia 822: | Linia 822: | ||
sformułowanie: | sformułowanie: | ||
<center><math> | <center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N: | ||
\sup_{x\in [0,1]}\big|f_n(x)-f(x)\big|<\varepsilon. | \sup_{x\in [0,1]}\big|f_n(x)-f(x)\big|<\varepsilon. | ||
</math></center> | </math></center> | ||
| Linia 829: | Linia 829: | ||
mamy równoważną postać | mamy równoważną postać | ||
<center><math> | <center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N | ||
\forall x\in X | \forall x\in X | ||
\big|f_n(x)-f(x)\big|<\varepsilon, | \big|f_n(x)-f(x)\big|<\varepsilon, | ||
| Linia 835: | Linia 835: | ||
a to oznacza, że | a to oznacza, że | ||
<math> | <math>f_n\rightrightarrows f</math> w <math>[0,1]</math> | ||
(patrz [[Analiza matematyczna 2/Wykład 4: Ciągi i szeregi funkcyjne. Szereg Taylora#def_4_1|definicja 4.1.]] (2)), | (patrz [[Analiza matematyczna 2/Wykład 4: Ciągi i szeregi funkcyjne. Szereg Taylora#def_4_1|definicja 4.1.]] (2)), | ||
co należało dowieść.<br> | co należało dowieść.<br> | ||
| Linia 841: | Linia 841: | ||
'''(4)''' | '''(4)''' | ||
Należy wykazać, że przestrzeń | Należy wykazać, że przestrzeń | ||
<math> | <math>C\big([0,1];\mathbb{R}\big)</math> jest zupełna. | ||
W tym celu weźmy dowolny ciąg Cauchy'ego | W tym celu weźmy dowolny ciąg Cauchy'ego | ||
<math> | <math>\displaystyle\{f_n\}\subseteq C\big([0,1];\mathbb{R}\big).</math> | ||
Należy pokazać, że ma on granicę w normie supremowej | Należy pokazać, że ma on granicę w normie supremowej | ||
(a zatem z punktu (3), że jest jednostajnie zbieżny). | (a zatem z punktu (3), że jest jednostajnie zbieżny). | ||
Zauważmy, że dla dowolnego <math> | Zauważmy, że dla dowolnego <math>x\in [0,1],</math> | ||
ciąg liczbowy <math> | ciąg liczbowy <math>\displaystyle\{f_n(x)\}</math> jest ciągiem Cauchy'ego | ||
(w <math> | (w <math>\displaystyle\mathbb{R}</math>), | ||
a zatem jest zbieżny, powiedzmy do <math> | a zatem jest zbieżny, powiedzmy do <math>f(x)</math> | ||
(korzystamy z zupełności <math> | (korzystamy z zupełności <math>\displaystyle\mathbb{R}</math>). | ||
Zatem <math> | Zatem <math>f</math> jest granicą punktową ciągu funkcyjnego | ||
<math> | <math>\displaystyle\{f_n\}.</math> | ||
Ustalmy <math> | Ustalmy <math>\displaystyle\varepsilon>0.</math> | ||
Z warunku Cauchy'ego wynika, że | Z warunku Cauchy'ego wynika, że | ||
<center><math> | <center><math>\exists N\in\mathbb{N}\ \forall m>n>N: | ||
\sup_{x\in[0,1]}\big|f_n(x)-f_m(x)\big| | \sup_{x\in[0,1]}\big|f_n(x)-f_m(x)\big| | ||
< | < | ||
| Linia 863: | Linia 863: | ||
</math></center> | </math></center> | ||
zatem dla <math> | zatem dla <math>m>n>N</math> mamy | ||
<center><math> | <center><math>\forall x\in[0,1]: | ||
\big|f_n(x)-f_m(x)\big| | \big|f_n(x)-f_m(x)\big| | ||
< | < | ||
| Linia 871: | Linia 871: | ||
</math></center> | </math></center> | ||
Dla ustalonego <math> | Dla ustalonego <math>x\in [0,1]</math> i ustalonego <math>n>N,</math> | ||
możemy przejść do granicy z <math> | możemy przejść do granicy z <math>m\rightarrow+\infty</math>, otrzymując | ||
<center><math> | <center><math>\big| f_n(x)-f(x)\big| | ||
\le | \le | ||
\varepsilon. | \varepsilon. | ||
</math></center> | </math></center> | ||
Zatem pokazaliśmy, że <math> | Zatem pokazaliśmy, że <math>f\rightrightarrows f,</math> | ||
czyli ciąg <math> | czyli ciąg <math>\displaystyle\{f_n\}</math> jest zbieżny w normie supremowej. | ||
W końcu korzystając | W końcu korzystając | ||
z twierdzenia o ciągłości granicy jednostajnie zbieżnego ciągu funkcji | z twierdzenia o ciągłości granicy jednostajnie zbieżnego ciągu funkcji | ||
ciągłych | ciągłych | ||
(patrz [[Analiza matematyczna 2/Wykład 4: Ciągi i szeregi funkcyjne. Szereg Taylora#tw_4_6|twierdzenie 4.6.]]), | (patrz [[Analiza matematyczna 2/Wykład 4: Ciągi i szeregi funkcyjne. Szereg Taylora#tw_4_6|twierdzenie 4.6.]]), | ||
mamy, że <math> | mamy, że <math>f\in C\big([0,1];\mathbb{R}\big).</math> | ||
</div></div> | </div></div> | ||
<span id="cw_3_6">{{cwiczenie|3.6.|| | <span id="cw_3_6">{{cwiczenie|3.6.|| | ||
Niech <math> | Niech <math>\displaystyle\|\cdot\|_1</math> i <math>\displaystyle\|\cdot\|_{\infty}</math> oznaczają odpowiednio | ||
normę taksówkową i maksimową w <math> | normę taksówkową i maksimową w <math>\displaystyle\mathbb{R}^N.</math> | ||
Pokazać, że | Pokazać, że | ||
<center><math> | <center><math>\|\cdot\|_{\square} | ||
= | = | ||
2\|\cdot\|_1+\|\cdot\|_{\infty} | 2\|\cdot\|_1+\|\cdot\|_{\infty} | ||
</math></center> | </math></center> | ||
jest normą w <math> | jest normą w <math>\displaystyle\mathbb{R}^N.</math> | ||
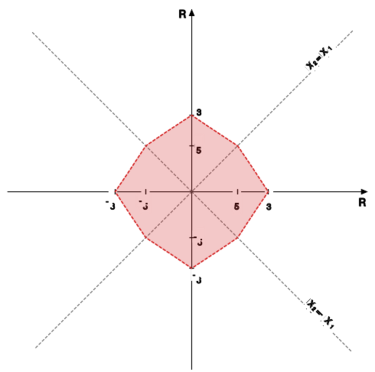
Dla <math> | Dla <math>N=2</math> narysować kulę | ||
<math> | <math>K\big((0,0),1\big)\subseteq\mathbb{R}^2</math> w tej normie. | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Korzystając z definicji norm | Korzystając z definicji norm | ||
<math> | <math>\displaystyle\|\cdot\|_1</math> i <math>\displaystyle\|\cdot\|_{\infty}</math>, | ||
pokazać, że <math> | pokazać, że <math>\displaystyle\|\cdot\|_{\square}</math> | ||
jest normą. | jest normą. | ||
</div></div> | </div></div> | ||
| Linia 913: | Linia 913: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:AM2.M03.C_R05.svg|375x375px|thumb|right|Kula w metryce z ćwiczenia 3.6.]] | [[File:AM2.M03.C_R05.svg|375x375px|thumb|right|Kula w metryce z ćwiczenia 3.6.]] | ||
Niech <math> | Niech <math>x\in\mathbb{R}^N.</math> | ||
Pokażemy, że | Pokażemy, że | ||
<math> | <math>\displaystyle\|x\|_{\square}=0\Longleftrightarrow x=\Theta.</math> | ||
Implikacja "<math> | Implikacja "<math>\displaystyle\Longleftarrow</math>" jest oczywista. | ||
W celu udowodnienia implikacji | W celu udowodnienia implikacji | ||
"<math> | "<math>\displaystyle\Longrightarrow</math>" załóżmy, że | ||
<math> | <math>\displaystyle\|x\|_{\square}=0.</math> | ||
Wówczas | Wówczas | ||
<math> | <math>2\|x\|_1+\|x\|_{\infty}=0,</math> czyli | ||
<math> | <math>\displaystyle\|x\|_1=0</math> i <math>\displaystyle\|x\|_{\infty}=0.</math> | ||
Ponieważ <math> | Ponieważ <math>\displaystyle\|\cdot\|_1</math> i <math>\displaystyle\|\cdot\|_{\infty}</math> | ||
są normami, więc <math> | są normami, więc <math>x=\Theta.</math> | ||
W celu pokazania jednorodności niech | W celu pokazania jednorodności niech | ||
<math> | <math>x\in \mathbb{R}^N</math> oraz <math>\displaystyle\lambda\in\mathbb{R}.</math> | ||
Wówczas | Wówczas | ||
| Linia 934: | Linia 934: | ||
<math> | <math> | ||
\begin{array}{lll} | \begin{array}{lll} | ||
\|\lambda x\|_{\square} | |||
& =& | & =& | ||
2\|\lambda x\|_1 | 2\|\lambda x\|_1 | ||
+\|\lambda x\|_{\infty} | +\|\lambda x\|_{\infty} | ||
| Linia 941: | Linia 941: | ||
2|\lambda| \|x\|_1 | 2|\lambda| \|x\|_1 | ||
+|\lambda| \|x\|_{\infty}\\ | +|\lambda| \|x\|_{\infty}\\ | ||
& =& | & =& | ||
|\lambda|\big(2\|x\|_1+\|x\|_{\infty}\big) | |\lambda|\big(2\|x\|_1+\|x\|_{\infty}\big) | ||
= | = | ||
| Linia 952: | Linia 952: | ||
W celu pokazania subaddytywności, | W celu pokazania subaddytywności, | ||
niech <math> | niech <math>x,y\in\mathbb{R}^N.</math> | ||
Wówczas | Wówczas | ||
<center> | <center> | ||
<math>\begin{array}{lll} | <math>\begin{array}{lll} | ||
\|x+y\|_{\square} | \|x+y\|_{\square} | ||
&=& | &=& | ||
2\|x+y\|_1 | 2\|x+y\|_1 | ||
+\|x+y\|_{\infty} | +\|x+y\|_{\infty} | ||
| Linia 965: | Linia 965: | ||
2\big(\|x\|_1+\|y\|_1\big) | 2\big(\|x\|_1+\|y\|_1\big) | ||
+\big(\|x\|_{\infty}+\|y\|_{\infty}\big)\\ | +\big(\|x\|_{\infty}+\|y\|_{\infty}\big)\\ | ||
&=& | &=& | ||
\big(2\|x\|_1+\|x\|_{\infty}\big) | \big(2\|x\|_1+\|x\|_{\infty}\big) | ||
\big(2\|y\|_1+\|y\|_{\infty}\big) | \big(2\|y\|_1+\|y\|_{\infty}\big) | ||
| Linia 974: | Linia 974: | ||
</center> | </center> | ||
Co kończy dowód, że <math> | Co kończy dowód, że <math>\displaystyle\|\cdot\|_{\square}</math> jest norma w | ||
<math> | <math>\displaystyle\mathbb{R}^N.</math><br> | ||
Aby narysować kulę | Aby narysować kulę | ||
<math> | <math>K\big((0,0),1\big)\subseteq\mathbb{R}^2</math> | ||
w tej normie, rozpiszmy wzór na tę normę: | w tej normie, rozpiszmy wzór na tę normę: | ||
<center> | <center> | ||
<math> | <math>\|(x_1,x_2)\|_{\square} | ||
= | = | ||
2|x_1|+2|x_2|+\max\big\{|x_1|+|x_2|\big\} | 2|x_1|+2|x_2|+\max\big\{|x_1|+|x_2|\big\} | ||
| Linia 988: | Linia 988: | ||
\left\{ | \left\{ | ||
\begin{array} {lll} | \begin{array} {lll} | ||
3|x_1|+2|x_2| & \text{jeśli} | 3|x_1|+2|x_2| & \text{jeśli} & |x_1|\ge |x_2|,\\ | ||
2|x_2|+3|x_2| & \text{jeśli} | 2|x_2|+3|x_2| & \text{jeśli} & |x_1|<|x_2|. | ||
\end{array} | \end{array} | ||
\right. | \right. | ||
| Linia 995: | Linia 995: | ||
</center> | </center> | ||
Zbiór punktów <math> | Zbiór punktów <math>(x_1,x_2)\in\mathbb{R}^2</math> spełniających | ||
nierówność <math> | nierówność <math>\displaystyle\|(x_1,x_2)\|_{\square}<1</math> dostajemy, rozpisując | ||
nierówności w poszczególnych ćwiartkach układu współrzędnych, | nierówności w poszczególnych ćwiartkach układu współrzędnych, | ||
dostajemy ośmiokąt jak na rysunku obok.<br> | dostajemy ośmiokąt jak na rysunku obok.<br> | ||
| Linia 1003: | Linia 1003: | ||
<span id="cw_3_7">{{cwiczenie|3.7.|| | <span id="cw_3_7">{{cwiczenie|3.7.|| | ||
Niech <math> | Niech <math>\displaystyle\|\cdot\|_1</math> i <math>\displaystyle\|\cdot\|_{\infty}</math> oznaczają odpowiednio | ||
normę taksówkową i maksimową w <math> | normę taksówkową i maksimową w <math>\displaystyle\mathbb{R}^N.</math> | ||
Sprawdzić, czy | Sprawdzić, czy | ||
<center><math> | <center><math>\|\cdot\|_{\circ} | ||
= | = | ||
2\|\cdot\|_1-\|\cdot\|_{\infty} | 2\|\cdot\|_1-\|\cdot\|_{\infty} | ||
</math></center> | </math></center> | ||
jest normą w <math> | jest normą w <math>\displaystyle\mathbb{R}^2.</math> | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Pokazać brak subaddytywności dla <math> | Pokazać brak subaddytywności dla <math>\displaystyle\|\cdot\|_{\circ}.</math> | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Pokażemy, że <math> | Pokażemy, że <math>\displaystyle\|\cdot\|_{\circ}</math> nie spełnia warunku | ||
subaddytywności. | subaddytywności. | ||
Dla wektorów | Dla wektorów | ||
<math> | <math>x=(1,0)</math> i <math>y(0,1)</math> w <math>\displaystyle\mathbb{R}^2</math> mamy | ||
<center><math> | <center><math>\|x+y\|_{\circ} | ||
= | = | ||
2\|(1,1)\|_1-\|(1,1)\|_{\infty} | 2\|(1,1)\|_1-\|(1,1)\|_{\infty} | ||
| Linia 1038: | Linia 1038: | ||
<center><math> | <center><math> | ||
\begin{array}{lll} | \begin{array}{lll} | ||
\|x\|_{\circ}+\|y\|_{\circ} | |||
& =& | & =& | ||
2\|(1,0)\|_1-\|(1,0)\|_{\infty}\\ | 2\|(1,0)\|_1-\|(1,0)\|_{\infty}\\ | ||
&+& 2\|(0,1)\|_1-\|(0,1)\|_{\infty} | &+& 2\|(0,1)\|_1-\|(0,1)\|_{\infty} | ||
| Linia 1046: | Linia 1046: | ||
Zatem | Zatem | ||
<math> | <math>\displaystyle\|x+y\|_{\circ}\not\le\|x\|_{\circ}+\|y\|_{\circ}.</math> | ||
Jako ciekawostkę proponujemy sprawdzenie, że dwa pierwsze | Jako ciekawostkę proponujemy sprawdzenie, że dwa pierwsze | ||
warunki w definicji normy zachodzą dla | warunki w definicji normy zachodzą dla | ||
<math> | <math>\displaystyle\|\cdot\|_{\circ}.</math> | ||
</div></div> | </div></div> | ||
<span id="cw_3_8">{{cwiczenie|3.8.|| | <span id="cw_3_8">{{cwiczenie|3.8.|| | ||
W <math> | W <math>\displaystyle\mathbb{R}^2</math> wprowadzamy | ||
<center><math> | <center><math>\big((x_1,x_2)|(y_1,y_2)\big)_{\triangle} | ||
= | = | ||
3x_1y_1+5x_2y_2 | 3x_1y_1+5x_2y_2 | ||
\quad </math> dla <math> | \quad </math> dla <math> \ \ (x_1,x_2),(y_1,y_2)\in\mathbb{R}^2. | ||
</math></center> | </math></center> | ||
'''(1)''' | '''(1)''' | ||
Pokazać, że <math> | Pokazać, że <math>\displaystyle\big(\cdot |\cdot \big)_{\triangle}</math> jest | ||
iloczynem skalarnym w <math> | iloczynem skalarnym w <math>\displaystyle\mathbb{R}^2.</math><br> | ||
'''(2)''' | '''(2)''' | ||
Jak wygląda <math> | Jak wygląda <math>\displaystyle\|\cdot\|_{\triangle}</math> | ||
norma zadana przez ten iloczyn skalarny? | norma zadana przez ten iloczyn skalarny? | ||
Obliczyć <math> | Obliczyć <math>\displaystyle\|(4,5)\|_{\triangle}.</math><br> | ||
'''(3)''' | '''(3)''' | ||
Dane są dwa wektory | Dane są dwa wektory | ||
<math> | <math>x=(1,7)</math> i <math>y=(3,a).</math> | ||
Dobrać parametr <math> | Dobrać parametr <math>a\in\mathbb{R}</math> tak, aby | ||
<math> | <math>x\perp y</math> (oczywiście w rozważanym iloczynie skalarnym).<br> | ||
'''(4)''' | '''(4)''' | ||
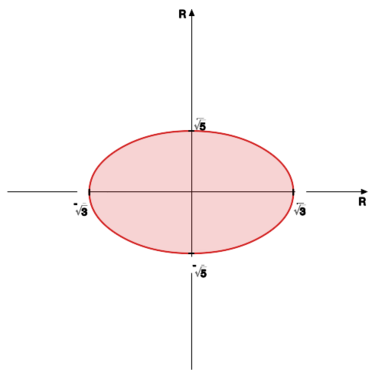
Narysować kulę <math> | Narysować kulę <math>K_{\triangle}\big((0,0),1\big)</math> | ||
w metryce zadanej przez ten | w metryce zadanej przez ten | ||
iloczyn skalarny. | iloczyn skalarny. | ||
| Linia 1099: | Linia 1099: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' | '''(1)''' | ||
Dla dowolnego <math> | Dla dowolnego <math>x=(x_1,x_2)\in\mathbb{R}^2</math> mamy | ||
<center><math> | <center><math>\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle} | ||
= | = | ||
3x_1^2+5x_2^2, | 3x_1^2+5x_2^2, | ||
| Linia 1108: | Linia 1108: | ||
zatem | zatem | ||
<center><math> | <center><math>\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle} | ||
\ge | \ge | ||
0 | 0 | ||
| Linia 1115: | Linia 1115: | ||
oraz | oraz | ||
<center><math> | <center><math>\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle}=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
(x_1,x_2)=\Theta, | (x_1,x_2)=\Theta, | ||
| Linia 1122: | Linia 1122: | ||
pokazaliśmy więc punkt (1) definicji iloczynu skalarnego. | pokazaliśmy więc punkt (1) definicji iloczynu skalarnego. | ||
Niech <math> | Niech <math>x=(x_1,x_2),y=(y_1,y_2)\in X</math> oraz <math>\displaystyle\lambda\in \mathbb{R}.</math> | ||
Wówczas | Wówczas | ||
<center><math> | <center><math> | ||
\begin{array}{lll} | \begin{array}{lll} | ||
\big(\lambda(x_1,x_2)|(y_1,y_2)\big)_{\triangle} | |||
&=& \displaystyle | &=& \displaystyle | ||
\big((\lambda x_1,\lambda x_2)|(y_1,y_2)\big)_{\triangle} | \big((\lambda x_1,\lambda x_2)|(y_1,y_2)\big)_{\triangle} | ||
| Linia 1142: | Linia 1142: | ||
Niech teraz | Niech teraz | ||
<math> | <math>x=(x_1,x_2),y=(y_1,y_2),z=(z_1,z_2)\in X.</math> | ||
Wówczas | Wówczas | ||
<center><math>\begin{array}{lll} | <center><math>\begin{array}{lll} | ||
\big((x_1,x_2)+(y_1,y_2)|(z_1,z_2)\big)_{\triangle} | |||
&=& | &=& | ||
\big((x_1+y_1,x_2+y_2)|(z_1,z_2)\big)_{\triangle}\\ | \big((x_1+y_1,x_2+y_2)|(z_1,z_2)\big)_{\triangle}\\ | ||
&=& | &=& | ||
| Linia 1153: | Linia 1153: | ||
&=& | &=& | ||
3x_1z_1+3y_1z_1+5x_2z_2+5y_2z_2\\ | 3x_1z_1+3y_1z_1+5x_2z_2+5y_2z_2\\ | ||
&=& | &=& | ||
\big(3x_1z_1+5x_2z_2\big) | \big(3x_1z_1+5x_2z_2\big) | ||
+\big(3y_1z_1+5y_2z_2\big)\\ | +\big(3y_1z_1+5y_2z_2\big)\\ | ||
| Linia 1163: | Linia 1163: | ||
pokazaliśmy więc punkt (3) definicji iloczynu skalarnego. | pokazaliśmy więc punkt (3) definicji iloczynu skalarnego. | ||
W końcu niech <math> | W końcu niech <math>x=(x_1,x_2),y=(y_1,y_2)\in X.</math> | ||
Wówczas | Wówczas | ||
<center><math> | <center><math>\big((x_1,x_2)|(y_1,y_2)\big)_{\triangle} | ||
= | = | ||
3x_1y_1+5y_1y_2 | 3x_1y_1+5y_1y_2 | ||
| Linia 1177: | Linia 1177: | ||
pokazaliśmy więc symetrię. | pokazaliśmy więc symetrię. | ||
Kończy to dowód faktu, że | Kończy to dowód faktu, że | ||
<math> | <math>(\cdot|\cdot)_{\triangle}</math> jest | ||
iloczynem skalarnym w <math> | iloczynem skalarnym w <math>\displaystyle\mathbb{R}^2.</math><br> | ||
<br> | <br> | ||
[[File:AM2.M03.C_R06.svg|375x375px|thumb|right|Kula w metryce zadanej przez iloczyn skalarny z ćwiczenia 3.8.]] | [[File:AM2.M03.C_R06.svg|375x375px|thumb|right|Kula w metryce zadanej przez iloczyn skalarny z ćwiczenia 3.8.]] | ||
'''(2)''' | '''(2)''' | ||
Ponieważ <math> | Ponieważ <math>(\cdot|\cdot)_{\triangle},</math> | ||
więc norma <math> | więc norma <math>\displaystyle\|\cdot\|_{\triangle}</math> | ||
zadana przez ten iloczyn skalarny | zadana przez ten iloczyn skalarny | ||
dla dowolnego <math> | dla dowolnego <math>x=(x_1,x_2)\in\mathbb{R}^2</math> | ||
wynosi: | wynosi: | ||
<center> | <center> | ||
<math> | <math>\|(x_1,x_2)\|_{\triangle} | ||
= | = | ||
\sqrt{\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle}} | \sqrt{\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle}} | ||
| Linia 1200: | Linia 1200: | ||
<center> | <center> | ||
<math> | <math>\|(4,5)\|_{\triangle} | ||
= | = | ||
\sqrt{3\cdot 4^2+5\cdot 5^2} | \sqrt{3\cdot 4^2+5\cdot 5^2} | ||
| Linia 1209: | Linia 1209: | ||
'''(3)''' | '''(3)''' | ||
Wektory <math> | Wektory <math>x</math> i <math>y</math> są ortogonalne wtedy i tylko wtedy, gdy | ||
<math> | <math>(x|y)_{\triangle}=0.</math> Zatem musimy rozwiązać równanie | ||
<center> | <center> | ||
<math> | <math>\big((1,7)|(3,a)\big)_{\triangle} | ||
= | = | ||
0, | 0, | ||
| Linia 1222: | Linia 1222: | ||
<center> | <center> | ||
<math> | <math>3\cdot 1\cdot 3+5\cdot 7\cdot a | ||
= | = | ||
0, | 0, | ||
| Linia 1229: | Linia 1229: | ||
skąd | skąd | ||
<math> | <math>a=-\frac{9}{35}.</math><br> | ||
<br> | <br> | ||
'''(4)''' | '''(4)''' | ||
| Linia 1235: | Linia 1235: | ||
<center> | <center> | ||
<math> | <math>\begin{align} | ||
K_{\triangle}\big((0,0),1\big) | K_{\triangle}\big((0,0),1\big) | ||
&= | &= | ||
| Linia 1251: | Linia 1251: | ||
Przypomnijmy, że zbiór punktów | Przypomnijmy, że zbiór punktów | ||
<math> | <math>(x_1,x_2)\in\mathbb{R}^2</math> | ||
spełniających równanie | spełniających równanie | ||
<math> | <math>\displaystyle\frac{x_1^2}{a^2}+\frac{x_2^2}{b^2}=1</math> jest elipsą o półosiach | ||
wielkich <math> | wielkich <math>a</math> i <math>b.</math> | ||
Zatem w naszym przypadku | Zatem w naszym przypadku | ||
zbiór punktów <math> | zbiór punktów <math>(x_1,x_2)\in\mathbb{R}^2</math> spełniających nierówność | ||
<math> | <math>\frac{x_1^2}{\frac{1}{3}}+\frac{x_2^2}{\frac{1}{5}}<1</math> | ||
jest wnętrzem elipsy o półosiach wielkich | jest wnętrzem elipsy o półosiach wielkich | ||
<math> | <math>\displaystyle\frac{1}{\sqrt{3}}</math> | ||
oraz <math> | oraz <math>\displaystyle\frac{1}{\sqrt{5}}.</math><br> | ||
</div></div> | </div></div> | ||
<span id="cw_3_9">{{cwiczenie|3.9.|| | <span id="cw_3_9">{{cwiczenie|3.9.|| | ||
(Zadanie nadobowiązkowe.) <br> | (Zadanie nadobowiązkowe.) <br> | ||
Niech <math> | Niech <math>X,Y</math> będą dwiema przestrzeniami unormowanymi oraz | ||
<math> | <math>f\colon X\longrightarrow Y</math> odwzorowaniem liniowym. | ||
Udowodnić, że następujące warunki są | Udowodnić, że następujące warunki są | ||
równoważne:<br> | równoważne:<br> | ||
'''(i)''' | '''(i)''' | ||
<math> | <math>f</math> jest ciągła;<br> | ||
'''(ii)''' | '''(ii)''' | ||
<math> | <math>\displaystyle\exists x_0\in X</math>: <math>f</math> jest ciągła w <math>x_0</math>;<br> | ||
'''(iii)''' | '''(iii)''' | ||
<math> | <math>f</math> jest ciągła w <math>\displaystyle\Theta\in X</math> | ||
(<math> | (<math>\Theta</math> oznacza wektor zerowy przestrzeni wektorowej <math>X</math>);<br> | ||
'''(iv)''' | '''(iv)''' | ||
<math> | <math>\displaystyle\exists M\ge 0\ \ \forall x\in X: | ||
\|x\|_X\le 1\ \Longrightarrow \big\|f(x)\big\|_Y\le M</math> | \|x\|_X\le 1\ \Longrightarrow \big\|f(x)\big\|_Y\le M</math> | ||
(to znaczy odwzorowanie <math> | (to znaczy odwzorowanie <math>f</math> jest ograniczone na domkniętej kuli o promieniu <math>1</math>);<br> | ||
'''(v)''' | '''(v)''' | ||
<math> | <math>\displaystyle\exists c\ge 0\ \ \forall x\in X: | ||
\big\|f(x)\big\|_Y\le c\|x\|_X</math> | \big\|f(x)\big\|_Y\le c\|x\|_X</math> | ||
(warunek ten nazywa się '''''ograniczonością dla odwzorowania liniowego''''');<br> | (warunek ten nazywa się '''''ograniczonością dla odwzorowania liniowego''''');<br> | ||
'''(vi)''' | '''(vi)''' | ||
<math> | <math>f</math> jest jednostajnie ciągła. | ||
}}</span> | }}</span> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Udowodnić kolejno implikacje | Udowodnić kolejno implikacje | ||
<math> | <math>(i)\Longrightarrow(ii)\Longrightarrow(iii)\Longrightarrow(iv)\Longrightarrow(v)\Longrightarrow(vi)\Longrightarrow(i).</math> | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
"<math> | "<math>(i)\Longrightarrow(ii)</math>"<br> | ||
Implikacja jest oczywista (z ciągłości funkcji wynika jej | Implikacja jest oczywista (z ciągłości funkcji wynika jej | ||
ciągłość w każdym punkcie).<br> | ciągłość w każdym punkcie).<br> | ||
<br> | <br> | ||
"<math> | "<math>(ii)\Longrightarrow(iii)</math>"<br> | ||
Załóżmy, że funkcja <math> | Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | ||
jest ciągła w pewnym punkcie <math> | jest ciągła w pewnym punkcie <math>x_0\in X.</math> | ||
Pokażemy, że jest ciągła w <math> | Pokażemy, że jest ciągła w <math>\displaystyle\Theta\in X.</math> | ||
Ustalmy dowolne <math> | Ustalmy dowolne <math>\displaystyle\varepsilon>0.</math> | ||
Z definicji Cauchy'ego ciągłości funkcji w punkcie wiemy, że | Z definicji Cauchy'ego ciągłości funkcji w punkcie wiemy, że | ||
<center><math> | <center><math>\exists \delta>0: | ||
\bigg[\|x-x_0\|_X\le\delta | \bigg[\|x-x_0\|_X\le\delta | ||
\ \Longrightarrow | \ \Longrightarrow | ||
| Linia 1312: | Linia 1312: | ||
</math></center> | </math></center> | ||
Dla dowolnego <math> | Dla dowolnego <math>z\in X</math> takiego, że | ||
<math> | <math>\displaystyle\|z\|_X\le\delta</math> niech | ||
<math> | <math>x=z+x_0.</math> | ||
Wówczas <math> | Wówczas <math>\displaystyle\|x-x_0\|_X=\|z\|_X\le\delta,</math> a zatem korzystając z | ||
powyższej implikacji, dostajemy, że | powyższej implikacji, dostajemy, że | ||
<math> | <math>\displaystyle\|f(z)\|_Y=\|f(x-x_0)\|_Y=\|f(x)-f(x_0)\|_Y\le\varepsilon.</math> | ||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
<center><math> | <center><math>\forall \varepsilon>0\ \exists \delta>0: | ||
\bigg[\|z\|_X\le\delta | \bigg[\|z\|_X\le\delta | ||
\ \Longrightarrow | \ \Longrightarrow | ||
| Linia 1326: | Linia 1326: | ||
</math></center> | </math></center> | ||
a to oznacza ciągłość funkcji <math> | a to oznacza ciągłość funkcji <math>f</math> w punkcie <math>\displaystyle\Theta.</math><br> | ||
<br> | <br> | ||
"<math> | "<math>(iii)\Longrightarrow(iv)</math>"<br> | ||
Załóżmy, że funkcja <math> | Załóżmy, że funkcja <math>f\colon X\longrightarrow Y</math> | ||
jest ciągła w punkcie <math> | jest ciągła w punkcie <math>\displaystyle\Theta.</math> | ||
Ustalmy <math> | Ustalmy <math>\displaystyle\varepsilon=1.</math> | ||
Wówczas | Wówczas | ||
<center><math> | <center><math>\exists \delta>0: | ||
\bigg[\|z\|_X\le\delta | \bigg[\|z\|_X\le\delta | ||
\ \Longrightarrow | \ \Longrightarrow | ||
| Linia 1340: | Linia 1340: | ||
</math></center> | </math></center> | ||
Niech <math> | Niech <math>M:=\frac{1}{\delta}.</math> | ||
Wówczas dla <math> | Wówczas dla <math>x\in X\setminus\{\Theta\}</math> takich, że <math>\displaystyle\|x\|_X\le 1</math> | ||
mamy | mamy | ||
<center><math> | <center><math>\|f(x)\|_Y | ||
= | = | ||
\bigg\|f\bigg(\frac{\delta x}{\delta}\bigg)\bigg\|_Y | \bigg\|f\bigg(\frac{\delta x}{\delta}\bigg)\bigg\|_Y | ||
| Linia 1352: | Linia 1352: | ||
Korzystając z faktów, że | Korzystając z faktów, że | ||
<math> | <math>\displaystyle\|x\|_X\le 1</math> oraz | ||
<math> | <math>\displaystyle\|\delta x\|_X=\delta\|x\|_X\le\delta</math> | ||
i z powyższej implikacji, | i z powyższej implikacji, | ||
dostajemy, że | dostajemy, że | ||
<center><math> | <center><math>\|f(x)\|_Y | ||
\le | \le | ||
\frac{1}{\delta} | \frac{1}{\delta} | ||
| Linia 1364: | Linia 1364: | ||
</math></center> | </math></center> | ||
Oczywiście dla <math> | Oczywiście dla <math>x=\Theta</math> implikacja także zachodzi. | ||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
<center><math> | <center><math>\forall x\in X: | ||
\bigg[ \|x\|_X\le 1 | \bigg[ \|x\|_X\le 1 | ||
\ \Longrightarrow | \ \Longrightarrow | ||
| Linia 1375: | Linia 1375: | ||
co należało dowieść.<br> | co należało dowieść.<br> | ||
<br> | <br> | ||
"<math> | "<math>(iv)\Longrightarrow(v)</math>"<br> | ||
Zakładamy, że | Zakładamy, że | ||
<center><math> | <center><math>\exists M>0 | ||
\forall x\in X: | \forall x\in X: | ||
\bigg[ \|x\|_X\le 1 | \bigg[ \|x\|_X\le 1 | ||
| Linia 1385: | Linia 1385: | ||
</math></center> | </math></center> | ||
Niech <math> | Niech <math>c:=M.</math> | ||
Wówczas dla dowolnego <math> | Wówczas dla dowolnego <math>x\in X\setminus\{\Theta\}</math> mamy | ||
<center><math> | <center><math>\big\|f(x)\big\|_X | ||
= | = | ||
\bigg\|f\bigg(\|x\|_X\frac{x}{\|x\|_X}\bigg)\bigg\|_X | \bigg\|f\bigg(\|x\|_X\frac{x}{\|x\|_X}\bigg)\bigg\|_X | ||
| Linia 1395: | Linia 1395: | ||
</math></center> | </math></center> | ||
Ponieważ <math> | Ponieważ <math>\displaystyle\bigg\|\frac{x}{\|x\|_X}\bigg\|_X=1,</math> | ||
więc możemy skorzystać z założenia, otrzymując | więc możemy skorzystać z założenia, otrzymując | ||
<center><math> | <center><math>\big\|f(x)\big\|_X | ||
= | = | ||
\|x\|_X\bigg\|f\bigg(\frac{x}{\|x\|_X}\bigg)\bigg\|_X | \|x\|_X\bigg\|f\bigg(\frac{x}{\|x\|_X}\bigg)\bigg\|_X | ||
| Linia 1407: | Linia 1407: | ||
</math></center> | </math></center> | ||
Oczywiście dla <math> | Oczywiście dla <math>x=\Theta</math> implikacja także jest prawdziwa. | ||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
<center><math> | <center><math>\exists c\ge 0\ \ \forall x\in X: | ||
\big\|f(x)\big\|_Y\le c\|x\|_X, | \big\|f(x)\big\|_Y\le c\|x\|_X, | ||
</math></center> | </math></center> | ||
| Linia 1416: | Linia 1416: | ||
co należało dowieść.<br> | co należało dowieść.<br> | ||
<br> | <br> | ||
"<math> | "<math>(v)\Longrightarrow(vi)</math>"<br> | ||
Zakładamy, że | Zakładamy, że | ||
<center><math> | <center><math>\exists c\ge 0\ \ \forall x\in X: | ||
\big\|f(x)\big\|_Y\le c\|x\|_X. | \big\|f(x)\big\|_Y\le c\|x\|_X. | ||
</math></center> | </math></center> | ||
W celu pokazania jednostajnej ciągłości funkcji <math> | W celu pokazania jednostajnej ciągłości funkcji <math>f</math> | ||
ustalmy dowolne <math> | ustalmy dowolne <math>\displaystyle\varepsilon>0.</math> | ||
Niech | Niech | ||
<math> | <math>\displaystyle\delta:=\frac{\varepsilon}{c}.</math> | ||
Wówczas dla dowolnych <math> | Wówczas dla dowolnych <math>x,z\in X</math> | ||
takich, że <math> | takich, że <math>\displaystyle\|x-z\|_X\le\delta,</math> | ||
korzystając z założenia, mamy | korzystając z założenia, mamy | ||
<center><math> | <center><math>\big\|f(x)-(z)\big\|_Y | ||
= | = | ||
\big\|f(x-z)\big\|_Y | \big\|f(x-z)\big\|_Y | ||
| Linia 1444: | Linia 1444: | ||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
<center><math> | <center><math>\forall \varepsilon>0\ \exists \delta>0 | ||
\forall x,z\in X: | \forall x,z\in X: | ||
\bigg[ \|x-z\|_X\le \delta | \bigg[ \|x-z\|_X\le \delta | ||
| Linia 1452: | Linia 1452: | ||
</math></center> | </math></center> | ||
co oznacza jednostajną ciągłość funkcji <math> | co oznacza jednostajną ciągłość funkcji <math>f.</math><br> | ||
<br> | <br> | ||
"<math> | "<math>(vi)\Longrightarrow(i)</math>"<br> | ||
Implikacja ta jest oczywista, gdyż jednostajna ciągłość zawsze | Implikacja ta jest oczywista, gdyż jednostajna ciągłość zawsze | ||
implikuje ciągłość | implikuje ciągłość | ||
(patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_37|twierdzenie 2.37.]]) | (patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_37|twierdzenie 2.37.]]) | ||
</div></div> | </div></div> | ||
Wersja z 08:42, 28 sie 2023
Norma. Iloczyn skalarny
Ćwiczenie 3.1.
W przestrzeni wektorowej definiujemy:
Pokazać, że oraz są normami (nazywamy je odpowiednio normą euklidesową, normą taksówkową oraz normą maksimową).
Ćwiczenie 3.2.
Pokazać, że norma euklidesowa zadaje metrykę euklidesową, norma taksówkowa zadaje metrykę taksówkową, a norma maksimowa zadaje metrykę maksimową.
Ćwiczenie 3.3.
Wykazać bezpośrednio równoważność norm: (taksówkowej), (euklidesowej) i (maksimowej) w znajdując optymalne stałe () w następujących nierównościach:
Ćwiczenie 3.4.
Niech i będą dwiema przestrzeniami wektorowymi.
Które z poniższych stwierdzeń są prawdziwe?
(Dla każdego podać dowód lub kontrprzykład).
(1)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(2)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(3)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(4)
Jeśli zbiory i
są wypukłe, to zbiór jest wypukły w
Ćwiczenie 3.5.
W przestrzeni wektorowej funkcji ciągłych na przedziale definiujemy:
(1)
Pokazać, że jest normą
w
Nazywamy ją normą supremową.
(2)
Obliczyć normę supremową dla funkcji:
oraz
(3)
Udowodnić, że zbieżność w normie supremowej pokrywa się ze
zbieżnością jednostajną dla funkcji ciągłych na
przedziale
(4) Pokazać, że z normą supremową jest przestrzenią Banacha.
(Punkty (3) i (4) są nadobowiązkowe. Potrzebne są tu pewne pojęcia z następnego wykładu. Do zadania można wrócić po następnym wykładzie).
Ćwiczenie 3.6.
Niech i oznaczają odpowiednio normę taksówkową i maksimową w Pokazać, że
jest normą w Dla narysować kulę w tej normie.
Ćwiczenie 3.7.
Niech i oznaczają odpowiednio normę taksówkową i maksimową w Sprawdzić, czy
jest normą w
Ćwiczenie 3.8.
W wprowadzamy
(1)
Pokazać, że jest
iloczynem skalarnym w
(2)
Jak wygląda
norma zadana przez ten iloczyn skalarny?
Obliczyć
(3)
Dane są dwa wektory
i
Dobrać parametr tak, aby
(oczywiście w rozważanym iloczynie skalarnym).
(4)
Narysować kulę
w metryce zadanej przez ten
iloczyn skalarny.
Ćwiczenie 3.9.
(Zadanie nadobowiązkowe.)
Niech będą dwiema przestrzeniami unormowanymi oraz
odwzorowaniem liniowym.
Udowodnić, że następujące warunki są
równoważne:
(i)
jest ciągła;
(ii)
: jest ciągła w ;
(iii)
jest ciągła w
( oznacza wektor zerowy przestrzeni wektorowej );
(iv)
(to znaczy odwzorowanie jest ograniczone na domkniętej kuli o promieniu );
(v)
(warunek ten nazywa się ograniczonością dla odwzorowania liniowego);
(vi)
jest jednostajnie ciągła.