Analiza matematyczna 2/Ćwiczenia 3: Norma. Iloczyn skalarny: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „<math> ” na „<math>” |
Nie podano opisu zmian |
||
| (Nie pokazano 2 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 16: | Linia 16: | ||
\stackrel{df}{=} | \stackrel{df}{=} | ||
\max_{1\le i\le N} |x_i| | \max_{1\le i\le N} |x_i| | ||
\quad</math> dla <math>\ x\in\mathbb{R}^N | \quad</math> dla <math>\ x\in\mathbb{R}^N</math></center> | ||
</math></center> | |||
Pokazać, że | Pokazać, że | ||
| Linia 53: | Linia 52: | ||
x_1=\ldots=x_N=0 | x_1=\ldots=x_N=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
x=\Theta | x=\Theta</math></center> | ||
</math></center> | |||
Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math>\lambda\in\mathbb{R}</math> | Dla <math>x=(x_1,\ldots,x_N)\in\mathbb{R}^N</math> oraz <math>\lambda\in\mathbb{R}</math> | ||
| Linia 67: | Linia 65: | ||
|\lambda|\sqrt{\sum_{i=1}^N x_i^2} | |\lambda|\sqrt{\sum_{i=1}^N x_i^2} | ||
= | = | ||
|\lambda|\|x\|_2 | |\lambda|\|x\|_2</math>,</center> | ||
</math></center> | |||
zatem pokazaliśmy warunek jednorodności. | zatem pokazaliśmy warunek jednorodności. | ||
| Linia 83: | Linia 80: | ||
\sum_{i=1}^Nx_i^2+ | \sum_{i=1}^Nx_i^2+ | ||
2\sum_{i=1}^Nx_iy_i | 2\sum_{i=1}^Nx_iy_i | ||
+\sum_{i=1}^Ny_i^2 | +\sum_{i=1}^Ny_i^2</math></center> | ||
</math></center> | |||
Korzystając z nierówności Cauchy'ego | Korzystając z nierówności Cauchy'ego | ||
| Linia 95: | Linia 91: | ||
\le | \le | ||
\bigg(\sum_{i=1}^N x_i^2\bigg) | \bigg(\sum_{i=1}^N x_i^2\bigg) | ||
\bigg(\sum_{i=1}^N y_i^2\bigg) | \bigg(\sum_{i=1}^N y_i^2\bigg)</math>,</center> | ||
</math></center> | |||
mamy | mamy | ||
| Linia 631: | Linia 626: | ||
<math>\lambda(a_1,b_1)+(1-\lambda)(a_2,b_2) | <math>\lambda(a_1,b_1)+(1-\lambda)(a_2,b_2) | ||
= | = | ||
\big(\lambda a_1+(1-\lambda)a_2,\lambda b_1+(1-\lambda)b_2\big) | \big(\lambda a_1+(1-\lambda)a_2,\lambda b_1+(1-\lambda)b_2\big)</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 640: | Linia 634: | ||
<center> | <center> | ||
<math>\lambda a_1+(1-\lambda)a_2\ \in\ A,\quad | <math>\lambda a_1+(1-\lambda)a_2\ \in\ A,\quad | ||
\lambda b_1+(1-\lambda)b_2\ \in\ B | \lambda b_1+(1-\lambda)b_2\ \in\ B</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 649: | Linia 642: | ||
<math>\big(\lambda a_1+(1-\lambda)a_2,\lambda b_1+(1-\lambda)b_2\big) | <math>\big(\lambda a_1+(1-\lambda)a_2,\lambda b_1+(1-\lambda)b_2\big) | ||
\ \in | \ \in | ||
A\times B | A\times B</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 713: | Linia 705: | ||
<center><math>\|f\|_{\infty}=0 | <center><math>\|f\|_{\infty}=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
f\equiv 0 | f\equiv 0</math></center> | ||
</math></center> | |||
Implikacja "<math>\Longrightarrow</math>" jest oczywista. | Implikacja "<math>\Longrightarrow</math>" jest oczywista. | ||
| Linia 776: | Linia 767: | ||
\sup_{x\in [0,1]}\big|f(x)\big| | \sup_{x\in [0,1]}\big|f(x)\big| | ||
+ | + | ||
\sup_{x\in [0,1]}\big|g(x)\big| | \sup_{x\in [0,1]}\big|g(x)\big|</math>,</center> | ||
</math></center> | |||
zatem biorąc supremum po lewej, stronie nierówność nadal jest | zatem biorąc supremum po lewej, stronie nierówność nadal jest | ||
| Linia 802: | Linia 792: | ||
\max\bigg\{\bigg|-\frac{1}{24}\bigg|,|1|,|2|\bigg\} | \max\bigg\{\bigg|-\frac{1}{24}\bigg|,|1|,|2|\bigg\} | ||
= | = | ||
2 | 2</math></center> | ||
</math></center> | |||
{| border="0" align="center" cellspacing="10" | {| border="0" align="center" cellspacing="10" | ||
| Linia 816: | Linia 805: | ||
<center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N: | <center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N: | ||
\|f_n-f\|_{\infty}<\varepsilon | \|f_n-f\|_{\infty}<\varepsilon</math></center> | ||
</math></center> | |||
Rozpisując normę supremową, otrzymujemy równoważne | Rozpisując normę supremową, otrzymujemy równoważne | ||
| Linia 823: | Linia 811: | ||
<center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N: | <center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N: | ||
\sup_{x\in [0,1]}\big|f_n(x)-f(x)\big|<\varepsilon | \sup_{x\in [0,1]}\big|f_n(x)-f(x)\big|<\varepsilon</math></center> | ||
</math></center> | |||
Z kolei korzystając z definicji supremum, | Z kolei korzystając z definicji supremum, | ||
| Linia 831: | Linia 818: | ||
<center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N | <center><math>\forall \varepsilon>0\ \exists N\in\mathbb{N}\ \forall n\ge N | ||
\forall x\in X | \forall x\in X | ||
\big|f_n(x)-f(x)\big|<\varepsilon | \big|f_n(x)-f(x)\big|<\varepsilon</math>,</center> | ||
</math></center> | |||
a to oznacza, że | a to oznacza, że | ||
| Linia 860: | Linia 846: | ||
\sup_{x\in[0,1]}\big|f_n(x)-f_m(x)\big| | \sup_{x\in[0,1]}\big|f_n(x)-f_m(x)\big| | ||
< | < | ||
\varepsilon | \varepsilon</math>,</center> | ||
</math></center> | |||
zatem dla <math>m>n>N</math> mamy | zatem dla <math>m>n>N</math> mamy | ||
| Linia 868: | Linia 853: | ||
\big|f_n(x)-f_m(x)\big| | \big|f_n(x)-f_m(x)\big| | ||
< | < | ||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Dla ustalonego <math>x\in [0,1]</math> i ustalonego <math>n>N</math>, | Dla ustalonego <math>x\in [0,1]</math> i ustalonego <math>n>N</math>, | ||
| Linia 876: | Linia 860: | ||
<center><math>\big| f_n(x)-f(x)\big| | <center><math>\big| f_n(x)-f(x)\big| | ||
\le | \le | ||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Zatem pokazaliśmy, że <math>f\rightrightarrows f</math>, | Zatem pokazaliśmy, że <math>f\rightrightarrows f</math>, | ||
| Linia 991: | Linia 974: | ||
2|x_2|+3|x_2| & \text{jeśli} & |x_1|<|x_2|. | 2|x_2|+3|x_2| & \text{jeśli} & |x_1|<|x_2|. | ||
\end{array} | \end{array} | ||
\right. | \right.</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 1060: | Linia 1042: | ||
= | = | ||
3x_1y_1+5x_2y_2 | 3x_1y_1+5x_2y_2 | ||
\quad</math> dla <math>\ \ (x_1,x_2),(y_1,y_2)\in\mathbb{R}^2 | \quad</math> dla <math>\ \ (x_1,x_2),(y_1,y_2)\in\mathbb{R}^2</math></center> | ||
</math></center> | |||
'''(1)''' | '''(1)''' | ||
| Linia 1103: | Linia 1084: | ||
<center><math>\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle} | <center><math>\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle} | ||
= | = | ||
3x_1^2+5x_2^2 | 3x_1^2+5x_2^2</math>,</center> | ||
</math></center> | |||
zatem | zatem | ||
| Linia 1117: | Linia 1097: | ||
<center><math>\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle}=0 | <center><math>\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle}=0 | ||
\ \Longleftrightarrow | \ \Longleftrightarrow | ||
(x_1,x_2)=\Theta | (x_1,x_2)=\Theta</math>,</center> | ||
</math></center> | |||
pokazaliśmy więc punkt (1) definicji iloczynu skalarnego. | pokazaliśmy więc punkt (1) definicji iloczynu skalarnego. | ||
| Linia 1193: | Linia 1172: | ||
\sqrt{\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle}} | \sqrt{\big((x_1,x_2)|(x_1,x_2)\big)_{\triangle}} | ||
= | = | ||
\sqrt{3x_1^2+5x_2^2} | \sqrt{3x_1^2+5x_2^2}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 1204: | Linia 1182: | ||
\sqrt{3\cdot 4^2+5\cdot 5^2} | \sqrt{3\cdot 4^2+5\cdot 5^2} | ||
= | = | ||
\sqrt{173} | \sqrt{173}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 1215: | Linia 1192: | ||
<math>\big((1,7)|(3,a)\big)_{\triangle} | <math>\big((1,7)|(3,a)\big)_{\triangle} | ||
= | = | ||
0 | 0</math>, | ||
</math> | |||
</center> | </center> | ||
| Linia 1224: | Linia 1200: | ||
<math>3\cdot 1\cdot 3+5\cdot 7\cdot a | <math>3\cdot 1\cdot 3+5\cdot 7\cdot a | ||
= | = | ||
0 | 0</math>, | ||
</math> | |||
</center> | </center> | ||
| Linia 1309: | Linia 1284: | ||
\bigg[\|x-x_0\|_X\le\delta | \bigg[\|x-x_0\|_X\le\delta | ||
\ \Longrightarrow | \ \Longrightarrow | ||
\|f(x)-f(x_0)\|_Y\le\varepsilon\bigg] | \|f(x)-f(x_0)\|_Y\le\varepsilon\bigg]</math></center> | ||
</math></center> | |||
Dla dowolnego <math>z\in X</math> takiego, że | Dla dowolnego <math>z\in X</math> takiego, że | ||
| Linia 1323: | Linia 1297: | ||
\bigg[\|z\|_X\le\delta | \bigg[\|z\|_X\le\delta | ||
\ \Longrightarrow | \ \Longrightarrow | ||
\|f(z)\|_Y\le\varepsilon\bigg] | \|f(z)\|_Y\le\varepsilon\bigg]</math>,</center> | ||
</math></center> | |||
a to oznacza ciągłość funkcji <math>f</math> w punkcie <math>\Theta</math>.<br> | a to oznacza ciągłość funkcji <math>f</math> w punkcie <math>\Theta</math>.<br> | ||
| Linia 1337: | Linia 1310: | ||
\bigg[\|z\|_X\le\delta | \bigg[\|z\|_X\le\delta | ||
\ \Longrightarrow | \ \Longrightarrow | ||
\|f(z)\|_Y\le 1\bigg] | \|f(z)\|_Y\le 1\bigg]</math></center> | ||
</math></center> | |||
Niech <math>M:=\frac{1}{\delta}</math>. | Niech <math>M:=\frac{1}{\delta}</math>. | ||
| Linia 1348: | Linia 1320: | ||
\bigg\|f\bigg(\frac{\delta x}{\delta}\bigg)\bigg\|_Y | \bigg\|f\bigg(\frac{\delta x}{\delta}\bigg)\bigg\|_Y | ||
= | = | ||
\frac{1}{\delta}\|f(\delta x)\|_Y | \frac{1}{\delta}\|f(\delta x)\|_Y</math></center> | ||
</math></center> | |||
Korzystając z faktów, że | Korzystając z faktów, że | ||
| Linia 1361: | Linia 1332: | ||
\frac{1}{\delta} | \frac{1}{\delta} | ||
= | = | ||
M | M</math></center> | ||
</math></center> | |||
Oczywiście dla <math>x=\Theta</math> implikacja także zachodzi. | Oczywiście dla <math>x=\Theta</math> implikacja także zachodzi. | ||
| Linia 1370: | Linia 1340: | ||
\bigg[ \|x\|_X\le 1 | \bigg[ \|x\|_X\le 1 | ||
\ \Longrightarrow | \ \Longrightarrow | ||
\big\|f(x)\big\|_Y\le M\bigg] | \big\|f(x)\big\|_Y\le M\bigg]</math>,</center> | ||
</math></center> | |||
co należało dowieść.<br> | co należało dowieść.<br> | ||
| Linia 1382: | Linia 1351: | ||
\bigg[ \|x\|_X\le 1 | \bigg[ \|x\|_X\le 1 | ||
\ \Longrightarrow | \ \Longrightarrow | ||
\big\|f(x)\big\|_Y\le M\bigg] | \big\|f(x)\big\|_Y\le M\bigg]</math></center> | ||
</math></center> | |||
Niech <math>c:=M</math>. | Niech <math>c:=M</math>. | ||
| Linia 1392: | Linia 1360: | ||
\bigg\|f\bigg(\|x\|_X\frac{x}{\|x\|_X}\bigg)\bigg\|_X | \bigg\|f\bigg(\|x\|_X\frac{x}{\|x\|_X}\bigg)\bigg\|_X | ||
= | = | ||
\|x\|_X\bigg\|f\bigg(\frac{x}{\|x\|_X}\bigg)\bigg\|_X | \|x\|_X\bigg\|f\bigg(\frac{x}{\|x\|_X}\bigg)\bigg\|_X</math></center> | ||
</math></center> | |||
Ponieważ <math>\bigg\|\frac{x}{\|x\|_X}\bigg\|_X=1</math>, | Ponieważ <math>\bigg\|\frac{x}{\|x\|_X}\bigg\|_X=1</math>, | ||
| Linia 1404: | Linia 1371: | ||
\|x\|_X\cdot M | \|x\|_X\cdot M | ||
= | = | ||
c\|x\|_X | c\|x\|_X</math></center> | ||
</math></center> | |||
Oczywiście dla <math>x=\Theta</math> implikacja także jest prawdziwa. | Oczywiście dla <math>x=\Theta</math> implikacja także jest prawdziwa. | ||
| Linia 1411: | Linia 1377: | ||
<center><math>\exists c\ge 0\ \ \forall x\in X: | <center><math>\exists c\ge 0\ \ \forall x\in X: | ||
\big\|f(x)\big\|_Y\le c\|x\|_X | \big\|f(x)\big\|_Y\le c\|x\|_X</math>,</center> | ||
</math></center> | |||
co należało dowieść.<br> | co należało dowieść.<br> | ||
| Linia 1420: | Linia 1385: | ||
<center><math>\exists c\ge 0\ \ \forall x\in X: | <center><math>\exists c\ge 0\ \ \forall x\in X: | ||
\big\|f(x)\big\|_Y\le c\|x\|_X | \big\|f(x)\big\|_Y\le c\|x\|_X</math></center> | ||
</math></center> | |||
W celu pokazania jednostajnej ciągłości funkcji <math>f</math> | W celu pokazania jednostajnej ciągłości funkcji <math>f</math> | ||
| Linia 1439: | Linia 1403: | ||
c\delta | c\delta | ||
= | = | ||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
| Linia 1449: | Linia 1412: | ||
\ \Longrightarrow | \ \Longrightarrow | ||
\big\|f(x)-f(z)\big\|_Y\le\varepsilon | \big\|f(x)-f(z)\big\|_Y\le\varepsilon | ||
\bigg] | \bigg]</math>,</center> | ||
</math></center> | |||
co oznacza jednostajną ciągłość funkcji <math>f</math>.<br> | co oznacza jednostajną ciągłość funkcji <math>f</math>.<br> | ||
Aktualna wersja na dzień 18:38, 12 wrz 2023
Norma. Iloczyn skalarny
Ćwiczenie 3.1.
W przestrzeni wektorowej definiujemy:
Pokazać, że oraz są normami (nazywamy je odpowiednio normą euklidesową, normą taksówkową oraz normą maksimową).
Ćwiczenie 3.2.
Pokazać, że norma euklidesowa zadaje metrykę euklidesową, norma taksówkowa zadaje metrykę taksówkową, a norma maksimowa zadaje metrykę maksimową.
Ćwiczenie 3.3.
Wykazać bezpośrednio równoważność norm: (taksówkowej), (euklidesowej) i (maksimowej) w , znajdując optymalne stałe () w następujących nierównościach:
Ćwiczenie 3.4.
Niech i będą dwiema przestrzeniami wektorowymi.
Które z poniższych stwierdzeń są prawdziwe?
(Dla każdego podać dowód lub kontrprzykład).
(1)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(2)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(3)
Jeśli zbiory są wypukłe, to zbiór jest wypukły.
(4)
Jeśli zbiory i
są wypukłe, to zbiór jest wypukły w .
Ćwiczenie 3.5.
W przestrzeni wektorowej , funkcji ciągłych na przedziale definiujemy:
(1)
Pokazać, że jest normą
w .
Nazywamy ją normą supremową.
(2)
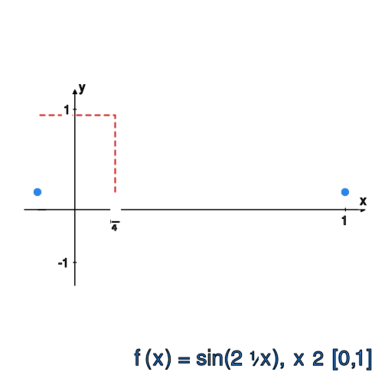
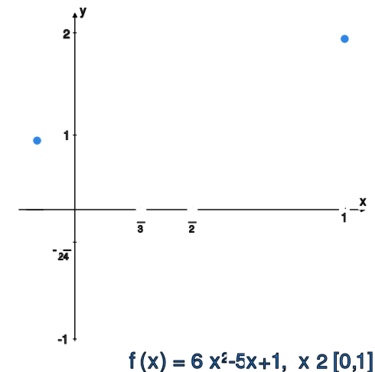
Obliczyć normę supremową dla funkcji:
oraz
.
(3)
Udowodnić, że zbieżność w normie supremowej pokrywa się ze
zbieżnością jednostajną dla funkcji ciągłych na
przedziale .
(4) Pokazać, że z normą supremową jest przestrzenią Banacha.
(Punkty (3) i (4) są nadobowiązkowe. Potrzebne są tu pewne pojęcia z następnego wykładu. Do zadania można wrócić po następnym wykładzie).
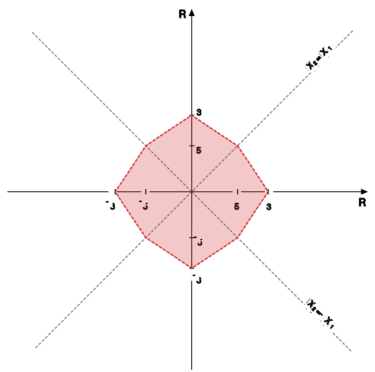
Ćwiczenie 3.6.
Niech i oznaczają odpowiednio normę taksówkową i maksimową w . Pokazać, że
jest normą w . Dla narysować kulę w tej normie.
Ćwiczenie 3.7.
Niech i oznaczają odpowiednio normę taksówkową i maksimową w . Sprawdzić, czy
jest normą w .
Ćwiczenie 3.8.
W wprowadzamy
(1)
Pokazać, że jest
iloczynem skalarnym w .
(2)
Jak wygląda
norma zadana przez ten iloczyn skalarny?
Obliczyć .
(3)
Dane są dwa wektory
i .
Dobrać parametr tak, aby
(oczywiście w rozważanym iloczynie skalarnym).
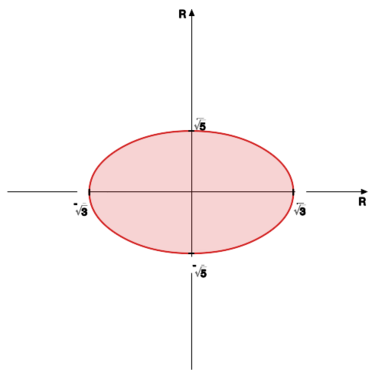
(4)
Narysować kulę
w metryce zadanej przez ten
iloczyn skalarny.
Ćwiczenie 3.9.
(Zadanie nadobowiązkowe.)
Niech będą dwiema przestrzeniami unormowanymi oraz
odwzorowaniem liniowym.
Udowodnić, że następujące warunki są
równoważne:
(i)
jest ciągła;
(ii)
: jest ciągła w ;
(iii)
jest ciągła w
( oznacza wektor zerowy przestrzeni wektorowej );
(iv)
(to znaczy odwzorowanie jest ograniczone na domkniętej kuli o promieniu );
(v)
(warunek ten nazywa się ograniczonością dla odwzorowania liniowego);
(vi)
jest jednostajnie ciągła.