Analiza matematyczna 2/Wykład 5: Szereg potęgowy. Trygonometryczny szereg Fouriera

Szereg potęgowy. Trygonometryczny szereg Fouriera

W tym wykładzie zajmujemy się najpierw szeregami potęgowymi. Definiujemy promień zbieżności i podajemy efektywny wzór na jego wyliczenie. Na przykładach badamy przedział zbieżności szeregu potęgowego. Podajemy twierdzenie mówiące o ciągłości sumy szeregu potęgowego oraz o różniczkowaniu szeregu potęgowego wyraz po wyrazie. Następnie zajmujemy się szeregami Fouriera. Podajemy definicję i wzory Eulera-Fouriera na współczynniki tego szeregu, jak też kryterium Dirichleta mówiące o jego zbieżności.

Szeregi potęgowe

Wśród szeregów funkcyjnych szczególną rolę odgrywają szeregi potęgowe, to znaczy szeregi, których wyrazy są jednomianami kolejnych stopni. Przykładem szeregu potęgowego jest szereg Taylora funkcji klasy $C^{\mathrm{\infty }}$.

Definicja 5.1.

Szeregiem potęgowym o środku w punkcie $x_0\in \mathbb{ℝ}$ i współrzędnych $c_n\in \mathbb{ℝ}$ ($n\in \mathbb{\mathbb{N}}$) nazywamy szereg funkcyjny postaci

$\sum _{n=0}^{\mathrm{\infty }}{c}_n(x-x_0{)}^n$

(umowa: $(x-x_0{)}^0=1$ nawet dla $x=x_0$).

Uwaga 5.2.

(1) Gdy $x_0=0$, to mamy szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$.
(2) Szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n(x-x_0{)}^n$ jest zawsze zbieżny w swoim środku, to znaczy dla $x=x_0$, bo wtedy dostajemy szereg zerowy.
(3) Dla wygody będziemy w dalszym wykładzie zakładali, że środek $x_0=0$, ale wszystkie twierdzenia można łatwo przenieść na przypadek, gdy środkiem jest dowolne $x_0\in \mathbb{ℝ}$.

Zacznijmy od kilku prostych obserwacji dotyczących szeregów potęgowych.

Twierdzenie 5.3.

Jeśli szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest zbieżny dla pewnego $x_1\ne 0$, to jest:
(1) bezwzględnie zbieżny dla dowolnego $|x|<|x_1|$;
(2) zbieżny jednostajnie na każdym przedziale $(-r,r)$, gdzie $r<|x_1|$.

Dowód 5.3. [nadobowiązkowy]

Zbieżność szeregu $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ dla $x_1$ oznacza zbieżność szeregu liczbowego $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}_1^n$, a to z kolei implikuje, że

$\lim {}_{n\to +\mathrm{\infty }}{c}_n{x}_1^n=0$

(patrz warunek konieczny zbieżności szeregów liczbowych; Analiza matematyczna 1 twierdzenie 6.3.). W szczególności ciąg $\{c_n{x}_1^n\}$ jest ograniczony, to znaczy

$\mathrm{\exists }M\in \mathbb{ℝ}\mathrm{\forall }n\in \mathbb{\mathbb{N}}:\left|c_n{x}_1^n\right|\le M$

Przystąpimy teraz do dowodu (1) i (2).
(Ad (1)) Niech $x$ będzie takie, że $|x|<|x_1|$. Wówczas

$\left|c_n{x}^n\right|=|c_n{x}_1^n\cdot \frac{x^n}{x_1^n}|=\left|\frac{x}{x_1}{|}^n\right|c_n{x}_1^n|\le M{q}^n$,

gdzie $q=\left|\frac{x}{x_1}\right|<1$. Możemy zatem zastosować kryterium porównawcze zbieżności szeregów (patrz Analiza matematyczna 1 twierdzenie 6.9.), z którego wynika, że szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest bezwzględnie zbieżny.
(Ad (2)) Niech $r<|x_1|$. Wówczas dla dowolnego $x$ takiego, że $|x|<r$ mamy

Karl Weierstrass (1815-1897)
Zobacz biografię

$\left|c_n{x}^n\right|=|c_n{x}_1^n\cdot \frac{x^n}{x_1}|\le M{q}^n$,

gdzie $q=\frac{r}{|x_1|}<1$ (zauważmy, że $q$ nie jest zależne od $x$). Korzystając z kryterium Weierstrassa zbieżności szeregów funkcyjnych (patrz twierdzenie 4.15.), wnioskujemy, że szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest zbieżny jednostajnie w przedziale $(-r,r)$.

Definicja 5.4.

Promieniem zbieżności szeregu potęgowego $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ nazywamy kres górny zbioru modułów wszystkich liczb $x$, dla których szereg ten jest zbieżny.

Uwaga 5.5.

Z twierdzenia 5.3. (1) wynika, że jeśli $R$ jest promieniem zbieżności szeregu $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$, to szereg ten jest zbieżny (i to bezwzględnie) w przedziale $(-R,R)$ oraz jest rozbieżny dla $|x|>R$. Tłumaczy to nazwę "promień zbieżności". Nic nie wiemy natomiast o zbieżności dla $x=R$ i $x=-R$. W każdej jednak sytuacji obszarem zbieżności szeregu potęgowego jest przedział w $\mathbb{ℝ}$.

Przykład 5.6.

Zbadać zbieżność szeregów:
(1) $\sum _{n=0}^{\mathrm{\infty }}{x}^n$;
(2) $\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}$;
(3) $\sum _{n=0}^{\mathrm{\infty }}{n}^n{x}^n$.

(Ad (1)) Jest to znany nam szereg geometryczny. Jest on zbieżny dla $|x|<1$ oraz rozbieżny dla $|x|\ge 1$ (gdyż dla $|x|\ge 1$ nie spełnia warunku koniecznego zbieżności szeregów; patrz Analiza matematyczna 1 twierdzenie 6.3.).
Zatem przedziałem zbieżności szeregu jest $(-1,1)$.
(Ad (2)) Jest to znany nam szereg Maclaurina dla funkcji $f(x)=e^x$ (patrz twierdzenie 4.19.). Promień zbieżności wynosi $R=+\mathrm{\infty }$, a obszarem zbieżności jest $\mathbb{ℝ}$.
(Ad (3)) Szereg ten jest zbieżny tylko dla $x=0$. Dla $x\ne 0$ nie spełnia on warunku koniecznego zbieżności szeregów. Zatem promieniem zbieżności jest $R=0$, a obszarem zbieżności

jest $\{0\}$.

Kolejne twierdzenie podaje efektywny wzór na liczenie promienia zbieżności szeregu potęgowego.

Twierdzenie 5.7.

Jeśli $R$ jest promieniem zbieżności szeregu $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ oraz $\kappa =\mathrm{lim\; sup}{}_{n\to +\mathrm{\infty }}\sqrt[n]{|c_n|}$,
to

$R=\{\begin{array}{ll}\frac{1}{\kappa }& \text{jeśli}0<\kappa <+\mathrm{\infty },\\ +\mathrm{\infty }& \text{jeśli}\kappa =0,\\ 0& \text{jeśli}\kappa =+\mathrm{\infty }.\end{array}$

Augustin Louis Cauchy (1789-1857)
Zobacz biografię

Dowód 5.7.

Przy ustalonym $x\in \mathbb{ℝ}$, zbadajmy zbieżność szeregu liczbowego $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$, korzystając z kryterium Cauchy'ego (patrz Analiza matematyczna 1 twierdzenie 7.4.). Dla $x\ne 0$, mamy:

$\mathrm{lim\; sup}{}_{n\to +\mathrm{\infty }}\sqrt[n]{|c_n{x}^n|}=\{\begin{array}{lll}\kappa |x|& \text{gdy}& \kappa <+\mathrm{\infty },\\ +\mathrm{\infty }& \text{gdy}& \kappa =+\mathrm{\infty }.\end{array}$

Przypadek 1. Gdy $\kappa \in (0,+\mathrm{\infty })$, to z kryterium Cauchy'ego (patrz Analiza matematyczna 1 twierdzenie 7.4.) wynika, że szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest zbieżny (bezwzględnie) dla $|x|<\frac{1}{\kappa }$ i rozbieżny dla $|x|>\frac{1}{\kappa }$. Zatem $R=\frac{1}{\kappa }$.
Przypadek 2. Gdy $\kappa =0$, to z kryterium Cauchy'ego wynika, że szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest zbieżny (bezwzględnie) dla $x\in \mathbb{ℝ}$. Zatem $R=+\mathrm{\infty }$.
Przypadek 3. Gdy $\kappa =+\mathrm{\infty }$, to z kryterium Cauchy'ego wynika, że szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest zbieżny tylko dla $x=0$. Zatem $R=0$.

Przykład 5.8.

Wyznacz przedziały zbieżności szeregów:
(1) $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}(x-2{)}^n$;
(2) $\sum _{n=2}^{\mathrm{\infty }}(-1{)}^n\frac{(x+1{)}^n}{n{\ln }^{2}n}$.

(Ad (1)) Korzystamy z twierdzenia 5.7. Mamy

$\kappa =\mathrm{lim\; sup}{}_{n\to +\mathrm{\infty }}\sqrt[n]{\frac{1}{n}}=1$

Zatem promień zbieżności wynosi $R=\frac{1}{\kappa }=1$, czyli szereg jest zbieżny w przedziale $(2-1,2+1)=(1,3)$ (zauważ, że środkiem szeregu jest tutaj $2$) oraz jest rozbieżny dla $x\in (-\mathrm{\infty },1)\cup (3,+\mathrm{\infty })$. Należy jeszcze zbadać zbieżność dla $x=1$ i dla $x=3$.
Dla $x=1$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n}{n}$, który jest zbieżny (wynika to z kryterium Leibniza; patrz Analiza matematyczna 1 wniosek 7.13 i przykład 7.14.; jest to znany nam szereg anharmoniczny).
Dla $x=3$ dostajemy szereg harmoniczny $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}$, który jest rozbieżny (patrz przykład 6.14.).
Zatem przedziałem zbieżności szeregu jest $[1,3)$.
(Ad (2)) Liczymy

$\kappa =\mathrm{lim\; sup}{}_{n\to +\mathrm{\infty }}\sqrt[n]{\frac{1}{n{\ln }^{2}n}}$

Oszacujmy wyrazy powyższego ciągu następująco:

$\sqrt[n]{\frac{1}{n^3}}\le \frac{1}{n{\ln }^{2}n}\le \sqrt[n]{\frac{1}{n}}$

Ponieważ ciągi po lewej i po prawej stronie mają granicę $1$, zatem z twierdzenia o trzech ciągach (patrz Analiza matematyczna 1 twierdzenie 4.11.) wnioskujemy, że $\kappa =1$. Zatem promień zbieżności wynosi $R=\frac{1}{\kappa }=1$, czyli szereg jest zbieżny w przedziale $(-1-1,-1+2)=(-2,0)$ (zauważ, że środkiem szeregu jest tutaj $-1$) oraz jest rozbieżny dla $x\in (-\mathrm{\infty },-2)\cup (0,+\mathrm{\infty })$. Należy jeszcze zbadań zbieżność dla $x=-2$ i dla $x=0$.
Dla $x=-2$ dostajemy szereg $\sum _{n=2}^{\mathrm{\infty }}\frac{1}{n{\ln }^{2}n}$, który jest zbieżny (można to pokazać, korzystając z kryterium całkowego, patrz Analiza matematyczna 1 przykład 14.27.).
Dla $x=0$ mamy szereg $\sum _{n=2}^{\mathrm{\infty }}\frac{(-1{)}^n}{n{\ln }^{2}n}$, który jest zbieżny (wynika to z kryterium Leibniza; patrz Analiza matematyczna 1 wniosek 7.13. lub też z faktu, że jest on bezwzględnie zbieżny, gdyż powyżej zbadaliśmy zbieżność szeregu modułów jego wyrazów).
Zatem przedziałem zbieżności szeregu jest

$[-2,0]$.

Wyrazy szeregu potęgowego (jednomiany $c_n{x}^n$) są funkcjami klasy $C^{\mathrm{\infty }}$. Interesującym jest pytanie o regularność sumy szeregu potęgowego, to znaczy, czy funkcja $S(x)=\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest ciągła, różniczkowalna, klasy $C^1$, klasy $C^{\mathrm{\infty }}$? Pierwsze z poniższych twierdzeń mówi, że suma szeregu jest funkcją ciągłą wewnątrz przedziału zbieżności.

Twierdzenie 5.9.

Suma szeregu potęgowego $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest funkcją ciągłą w przedziale $(-R,R)$, gdzie $R>0$ jest promieniem zbieżności tego szeregu.

Rysunek do dowodu twierdzenia 5.9.

Dowód 5.9.

Niech $R>0$ będzie promieniem zbieżności szeregu $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ (gdy $R=0$, teza jest pusto spełniona). Niech $x\in (-R,R)$. Z własności zbioru liczb rzeczywistych wynika, że

$\mathrm{\exists }r\in \mathbb{ℝ}:|x|<r<R$

Z twierdzenia 5.3. (2) wynika, że szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest jednostajnie zbieżny w $(-r,r)$. Ponieważ funkcje $f_n(x)=c_n{x}^n$ są ciągłe, więc korzystając z twierdzenia 4.13., dostajemy, że suma tego szeregu jest także funkcją ciągłą w $x$. Ponieważ punkt $x\in (-R,R)$ był dowolnie wybrany, więc suma szeregu jest funkcją ciągłą w przedziale $(-R,R)$.

Kolejne twierdzenie mówi, że wewnątrz przedziału zbieżności suma szeregu potęgowego jest nie tylko ciągła, ale także różniczkowalna oraz pochodna sumy szeregu jest sumą szeregu pochodnych wyrazów szeregu wyjściowego. Dowód tego twierdzenia pomijamy.

Twierdzenie 5.10. [o różniczkowaniu szeregu potęgowego wyraz po wyrazie]]

Suma szeregu potęgowego $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$ jest funkcją różniczkowalną w każdym punkcie przedziału $(-R,R)$, gdzie $R>0$ jest promieniem zbieżności tego szeregu, a pochodna tej sumy wyraża się wzorem

$f^{\prime }(x)=\sum _{n=0}^{\mathrm{\infty }}(n+1)c_{n+1}{x}^n\mathrm{\forall }x\in (-R,R)$

W szczególności szereg $\sum _{n=0}^{\mathrm{\infty }}(n+1)c_{n+1}{x}^n$ ma ten sam promień zbieżności co wyjściowy szereg $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$.

Uwaga 5.11.

Z powyższego twierdzenia wynika, że pochodna sumy szeregu potęgowego jest też sumą pewnego szeregu potęgowego oraz że jest ona funkcją ciągłą. Zatem suma szeregu potęgowego jest funkcją klasy $C^1$. To samo możemy zastosować do pochodnej, itd. Zatem suma szeregu potęgowego jest funkcją klasy $C^{\mathrm{\infty }}$.

Przykład 5.12.

Korzystając z twierdzenia 5.10. oraz ze znajomości szeregów Maclaurina dla funkcji $e^x$, $\sin x$ i $\cos x$ oblicz pochodne tych funkcji.

(1) Ponieważ

$e^x=\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}\mathrm{\forall }x\in \mathbb{ℝ}$,

(patrz twierdzenie 4.19.), zatem

$(e^x{)}^{\prime }=\sum _{n=0}^{\mathrm{\infty }}\left(\frac{x^n}{n!}\right)=\sum _{n=1}^{\mathrm{\infty }}\frac{x^{n-1}}{(n-1)!}=\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}=e^x$

(2) Ponieważ

$\sin x=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n+1}}{(2n+1)!}\mathrm{\forall }x\in \mathbb{ℝ}$,

zatem

$(\sin x{)}^{\prime }=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{(2n+1)x^{2n}}{(2n+1)!}=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n}}{(2n)!}=\cos x$

(3) Ponieważ

$\cos x=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n}}{(2n)!}\mathrm{\forall }x\in \mathbb{ℝ}$,

zatem

$\begin{array}{rl}(\cos x{)}^{\prime }& =\sum _{n=1}^{\mathrm{\infty }}(-1{)}^n\frac{2n{x}^{2n-1}}{(2n)!}=\sum _{n=1}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n-1}}{(2n-1)!}=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^{n+1}\frac{x^{2n+1}}{(2n+1)!}\\ & =-\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n+1}}{(2n+1)!}=-\sin x.\end{array}$

Wiemy już, że każdy szereg Taylora jest szeregiem potęgowym. Zadamy teraz pytanie odwrotne. Weźmy dowolny szereg potęgowy $\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$. Czy szereg ten jest szeregiem Taylora pewnej funkcji? Mówi o tym poniższa uwaga.

Uwaga 5.13.

Rozważmy szereg potęgowy $\sum _{n=0}^{\mathrm{\infty }}{c}_n(x-x_0{)}^n$. Niech $R$ będzie promieniem zbieżności tego szeregu.

Wiemy, że szereg ten jest zbieżny dla $x$ takich, że $|x-x_0|<R$ oraz jest rozbieżny dla $x$ takich, że $|x-x_0|>R$.

Jeśli $R>0$, to funkcja

$f(x)=\sum _{n=0}^{\mathrm{\infty }}{c}_n(x-x_0{)}^n$ dla $x\in (x_0-R,x_0+R)$

jest klasy $C^{\mathrm{\infty }}$ na przedziale $(x_0-R,x_0+R)$ (patrz uwaga 5.11.) oraz

$\begin{array}{rl}{f}^{\prime }(x)& =\sum _{n=0}^{\mathrm{\infty }}(n+1)c_{n+1}(x-x_0{)}^n,\\ ⋮& & \\ f^{(k)}(x)& =\sum _{n=0}^{\mathrm{\infty }}(n+k)\cdot \dots \cdot (n+1)c_{n+k}(x-x_0{)}^n.\end{array}$

Wstawiając $x=x_0$, dostajemy

$f^{(k)}(x_0)=k!c_k$,

czyli

$c_n=\frac{f^{(n)}(x_0)}{n!}$ dla $n\in \mathbb{\mathbb{N}}$

ale to są dokładnie współczynniki we wzorze Taylora. Zatem:
(1) Szereg potęgowy jest szeregiem Taylora swojej sumy wewnątrz obszaru zbieżności.
(2) Przedstawienie danej funkcji w szereg potęgowy jest jednoznaczne i tym szeregiem jest szereg Taylora.

Szeregi trygonometryczne Fouriera

Funkcje $\sin x$ i $\cos x$

Jean Baptiste Joseph Fourier (1768-1830)
Zobacz biografię

Przypomnijmy, że funkcję $f:\mathbb{ℝ}\to \mathbb{ℝ}$ nazywamy okresową, jeśli istnieje liczba $T>0$ taka, że dla wszystkich $x\in R$

$f(x+T)=f(x)$

Przykład 5.14.

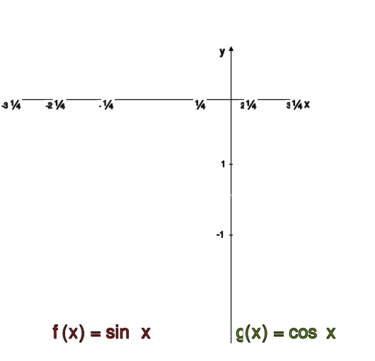
Funkcjami okresowymi są na przykład funkcje sinus i cosinus. Patrz rysunek obok.

Innym przykładem funkcji okresowej jest mantysa, czyli funkcja $m(x):=x-[x]$ (patrz rysunek poniżej).

Funkcję okresową możemy także otrzymać, biorąc na przykład następującą sumę:

$f(x)=\sin (x)+\frac{1}{2}\sin (2x)+\frac{1}{2}\sin (3x)$

Ogólnie, zauważmy, że biorąc skończoną sumę

$s(x)=\sum _{j=1}^n{a}_j\cos jx+b_j\sin jx$,

ze stałymi (rzeczywistymi) współczynnikami $a_j$ i $b_j$, dostaniemy funkcję okresową.

Plik:AM2.M05.W.R03.svg $m(x)=x-[x]$

<flash>file=AM2.M05.W.R04.swf|width=375|height=375</flash> <div.thumbcaption>$f(x)=\sin (x)+\frac{1}{2}\sin (2x)+\frac{1}{2}\sin (3x)$

Problem:
Można zatem zadać sobie pytanie: czy biorąc dowolną funkcję okresowa, możemy ją przedstawić w postaci takiej sumy jak powyżej?

Okazuje się, że jest to dla dużej ilości funkcji możliwe, jeśli zamiast sum skończonych będziemy rozważać sumy nieskończone, czyli szeregi.

Konstrukcja:
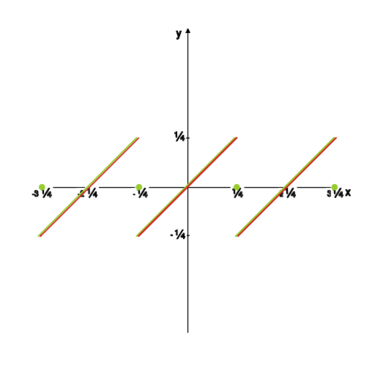
Weźmy zatem funkcję okresową $f:\mathbb{ℝ}\to \mathbb{ℝ}$. Załóżmy, że ma ona okres $2\pi$, i że na przedziale $[-\pi ,\pi ]$ funkcja jest całkowalna.

Przykłady funkcji spełniających te założenia są na rysunku poniżej:

Funkcja okresowa o okresie $2\pi$

Plik:AM2.M05.W.R06.svg Funkcja okresowa o okresie $2\pi$

Przypuśćmy teraz, że możemy zapisać $f$ jako sumę szeregu zbieżnego jednostajnie, z pewnymi stałymi współczynnikami $a_n$ i $b_n$:

$(★)f(x)=a_0+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (nx)+b_n\sin (nx)$,

Pokażemy teraz, że czy istnieją ogólne wzory na współczynniki $a_n$ i $b_n$. Aby znaleźć $a_0$, scałkujmy obie strony wzoru $(★)$ od $-\pi$ do $\pi$. Dostaniemy wtedy:

$\underset{-\pi }{\overset{\pi }{\int }}f(x)dx=\underset{-\pi }{\overset{\pi }{\int }}{a}_{0}dx+\sum _{n=1}^{\mathrm{\infty }}(a_n\underset{-\pi }{\overset{\pi }{\int }}\cos (nx)dx+b_n\underset{-\pi }{\overset{\pi }{\int }}\sin (nx)dx)$

Zauważmy, że

$\underset{-\pi }{\overset{\pi }{\int }}\cos (nx)dx=\frac{\sin (nx)}{n}{|}_{-\pi }^{\pi }=0$,

oraz

$\underset{-\pi }{\overset{\pi }{\int }}\sin (nx)dx=-\frac{\cos (nx)}{n}{|}_{-\pi }^{\pi }=0$

Dostajemy zatem:

$\underset{-\pi }{\overset{\pi }{\int }}f(x)dx=2\pi a_0$,

czyli

$a_0=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)dx$

Aby wyliczyć $a_m,m=1,2,3,\dots$, pomnóżmy obie strony wzoru $(★)$ przez $\cos (mx)$ i, tak jak powyżej, całkujmy od $-\pi$ do $\pi$.

Dostaniemy wtedy

$\begin{array}{lll}(★★)\underset{-\pi }{\overset{\pi }{\int }}f(x)\cos (mx)dx& =& \underset{-\pi }{\overset{\pi }{\int }}{a}_0\cos (mx)dx\\ & +& \sum _{n=1}^{\mathrm{\infty }}(a_n\underset{-\pi }{\overset{\pi }{\int }}\cos (nx)\cos (mx)dx+b_n\underset{-\pi }{\overset{\pi }{\int }}\sin (nx)\cos (mx)dx).\end{array}$

Teraz

$a_0\underset{-\pi }{\overset{\pi }{\int }}\cos (mx)dx=a_0\frac{\sin (mx)}{m}{|}_{-\pi }^{\pi }=0$

Dla $m\ne n$ dostaniemy, korzystając ze wzoru na sumę cosinusów

$a_n\underset{-\pi }{\overset{\pi }{\int }}\cos (nx)\cos (mx)dx=\frac{1}{2}\underset{-\pi }{\overset{\pi }{\int }}(\cos ((n+m)x)+\cos ((n-m)x))dx$,

a korzystając ze wzoru na sumę sinusów, mamy

$b_n\underset{-\pi }{\overset{\pi }{\int }}\sin (nx)\cos (mx)dx=\frac{1}{2}\underset{-\pi }{\overset{\pi }{\int }}(\sin ((n+m)x)+\sin ((n-m)x))dx$

Obliczając, dostajemy

$\frac{1}{2}\underset{-\pi }{\overset{\pi }{\int }}(\cos ((n+m)x)+\cos ((n-m)x))dx=0$

oraz

$\frac{1}{2}\underset{-\pi }{\overset{\pi }{\int }}(\sin ((n+m)x)+\sin ((n-m)x))dx=0$

Natomiast gdy $m=n$ dostajemy

$a_m\underset{-\pi }{\overset{\pi }{\int }}{\cos }^2(mx)dx=\pi a_m$

Tak więc widzimy, że z prawej strony wzoru $(★★)$ znikają wszystkie całki, poza całką o współczynniku $a_m$, a zatem otrzymujemy wzór:

$a_m=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\cos (mx)dx$

Analogicznie, mnożąc obie strony wzoru $(★)$ przez $\sin (mx)$, wyznaczamy wzory na współczynniki $b_m$:

$b_m=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\sin (mx)dx$

(pozostawiamy to jako ćwiczenie).

Możemy teraz wypisać definicję.

Leonhard Euler (1707-1783)
Zobacz biografię

Definicja 5.15.

Dla funkcji okresowej $f:\mathbb{ℝ}\to \mathbb{ℝ}$, o okresie $2\pi$, i całkowalnej na $[-\pi ,\pi ]$ tworzymy szereg

$\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (nx)+b_n\sin (nx)$,

ze współczynnikami

$\begin{array}{rl}{a}_0& =\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)dx,\\ a_m& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\cos (mx)dx,m=1,2,\dots ,\\ b_m& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\sin (mx)dxm=1,2...\end{array}$

Szereg ten nazywamy szeregiem Fouriera funkcji $f$. Wzory na współczynniki nazywają się wzorami Eulera-Fouriera.

Powyższa konstrukcja pokazuje, że prawdziwe jest następujące stwierdzenie.

Wykres funkcji oraz sumy jej szeregu Fouriera

Stwierdzenie 5.16.

Jeśli funkcję $f:\mathbb{ℝ}\to \mathbb{ℝ}$, okresową, o okresie $2\pi$, całkowalną na $[-\pi ,\pi ]$, możemy zapisać w postaci jednostajnie zbieżnego szeregu:

$f(x)=a_0+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (nx)+b_n\sin (nx)$,

to współczynniki $a_n$ i $b_n$ wyrażają się wzorami Eulera-Fouriera. (Tak więc przy powyższych założeniach mamy jednoznaczne przedstawienie $f$ w postaci sumy szeregu trygonometrycznego.)

Uwaga 5.17.

Na początku tej części wykładu założyliśmy, że we wzorze $(★)$ zachodzi równość, a co więcej, że szereg po prawej stronie tego wzoru jest zbieżny jednostajnie. Zazwyczaj jednak mamy daną funkcję $f$, ale nie mamy danego szeregu $a_0+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (nx)+b_n\sin (nx)$, tym bardziej nic nie wiemy o jego zbieżności.

Zauważmy jednak, że zawsze możemy wypisać formalnie szereg Fouriera dla danej funkcji (oczywiście dla funkcji spełniającej nasze założenia, czyli okresowej i całkowalnej).

Piszemy wówczas:

$f(x)\sim a_0+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (nx)+b_n\sin (nx)$,

gdzie współczynniki $a_n$ i $b_n$ są wyliczone ze wzorów Eulera-Fouriera. Utworzyliśmy zatem szereg Fouriera funkcji $f$, ale pozostaje pytanie, kiedy i do czego ten szereg jest zbieżny. Zaznaczmy, że suma szeregu Fouriera danej funkcji wcale nie musi być równa tej funkcji.

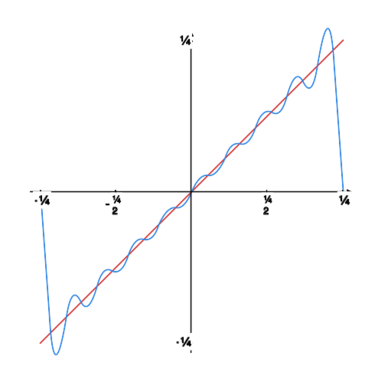
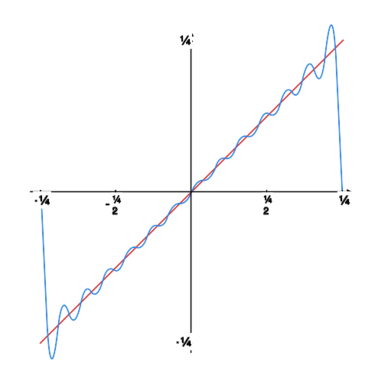
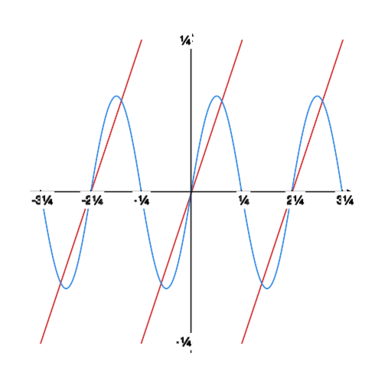
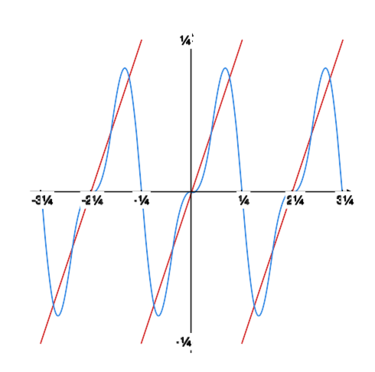
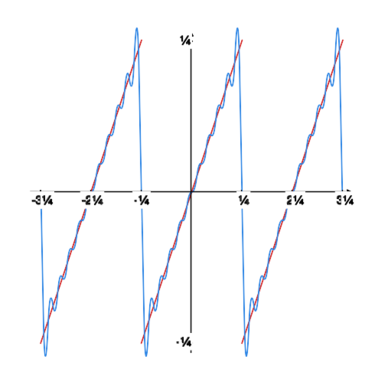
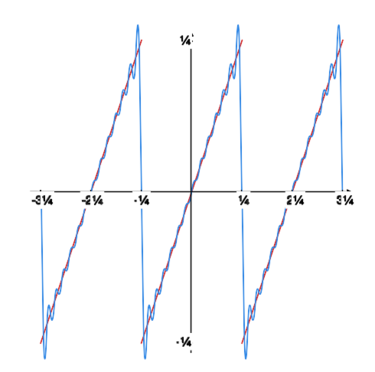
Na rysunku obok widzimy wykres funkcji (zielony) i wykres sumy szeregu Fouriera tej funkcji (czerwony).

Jedną z odpowiedzi na pytanie o zbieżność szeregu Fouriera daje poniższe kryterium Dirichleta (które podajemy bez dowodu):

Johann Peter Gustav Lejeune Dirichlet (1805-1859)
Zobacz biografię

Twierdzenie 5.18. [Kryterium Dirichleta]

Załóżmy, że funkcja $f(x)$ o okresie $2\pi$ jest przedziałami monotoniczna w $[-\pi ,\pi ]$ (to znaczy, że przedział $[-\pi ,\pi ]$ można podzielić na skończoną liczbę przedziałów, w których funkcja jest monotoniczna) i ma co najwyżej skończoną liczbę punktów nieciągłości. Wówczas w każdym punkcie ciągłości $x_0$

$f(x_0)=a_0+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (n{x}_0)+b_n\sin (n{x}_0)$

Co więcej, dla każdego punktu nieciągłości $y_0$

$a_0+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (n{y}_0)+b_n\sin (n{y}_0)=\frac{f(y_0^{+})+f(y_0^{-})}{2}$,

gdzie zapis $f(y_0^{-})$ oznacza lewostronną granicę funkcji w punkcie $y_0$ a zapis $f(y_0^{+})$ - granicę prawostronną.

Typowy przykład funkcji spełniającej założenia powyższego kryterium jest przedstawiony na rysunku powyżej (wykres funkcji jest zielony, a wykres sumy szeregu Fouriera czerwony).

Plik:AM2.M05.W.R06.svg

Funkcja $f(x)=x$  rozszerzona okresowo

Uwaga 5.19.

W zastosowaniach często mamy do czynienia z funkcjami nieokresowymi, zadanymi w przedziale $(-\pi ,\pi ]$. W takich przypadkach musimy funkcję $f$ na całe $\mathbb{ℝ}$ rozszerzyć okresowo.

Może się też zdarzyć, że będziemy chcieli rozwinąć w szereg Fouriera funkcję $f$ okresową, ale o okresie $2T$ (a nie $2\pi$). Stosujemy wówczas podstawienie $x=\frac{Ty}{\pi }$ i dostajemy wzory na współczynniki:

$\begin{array}{rl}{a}_0& =\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}f(\frac{Ty}{\pi })dy,\\ a_m& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(\frac{Ty}{\pi })\cos (my)dy,m=1,2,\dots \\ b_m& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(\frac{Ty}{\pi })\sin (my)dym=1,2,\dots \end{array}$

Dostajemy zatem rozwinięcie

$f(\frac{Ty}{\pi })=a_0+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (ny)+b_n\sin (ny)$,

czyli wracając do zmiennej $x$:

$f(x)=a_0+\sum _{n=1}^{\mathrm{\infty }}{a}_n\cos (\frac{n\pi x}{T})+b_n\sin (\frac{n\pi x}{T})$

Przykład 5.20.

Rozwinąć w szereg Fouriera funkcję $f(x)=x^2$ zadaną na przedziale $[-\pi ,\pi ]$.

Liczymy współczynniki:

$\begin{array}{rl}{a}_0& =\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}{x}^{2}dx=\frac{{\pi }^2}{3},\\ a_n& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}{x}^2\cos (nx)dx=\frac{2}{\pi }\underset{0}{\overset{\pi }{\int }}{x}^2\cos (nx)dx\\ & =\frac{2}{\pi }{x}^2\frac{\sin (nx)}{n}{|}_0^{\pi }-\frac{4}{n\pi }\underset{0}{\overset{\pi }{\int }}x\sin (nx)dx\\ & =\frac{4}{n\pi }x\frac{\cos (nx)}{n}{|}_0^{\pi }-\frac{4}{n^2\pi }\underset{0}{\overset{\pi }{\int }}\cos (nx)dx=(-1{)}^n\frac{4}{n^2}.\end{array}$

Jako ćwiczenie zauważmy, że wszystkie współczynniki $b_n$ są równe zero.

Tak więc, skoro nasza funkcja spełnia warunki powyższego kryterium zbieżności, możemy napisać:

$x^2=\frac{{\pi }^2}{3}+4\sum _{n=1}^{\mathrm{\infty }}(-1{)}^n\frac{\cos (nx)}{\pi }$

Podstawiając w tym wzorze $x=\pi$ i pamiętając, że $\cos (n\pi )=(-1{)}^n$, otrzymujemy

${\pi }^2=\frac{{\pi }^2}{3}+4\sum _{n=1}^{\mathrm{\infty }}(-1{)}^n\frac{(-1{)}^n}{n^2}$,

czyli

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}=\frac{{\pi }^2}{6}$,

zatem nie tylko wykazaliśmy zbieżność szeregu $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}$, ale nawet policzyliśmy jego sumę.

Rysunek obok oraz rysunki poniżej pokazują, jak kolejne sumy częściowe szeregu Fouriera „zbliżają się” do granicy.

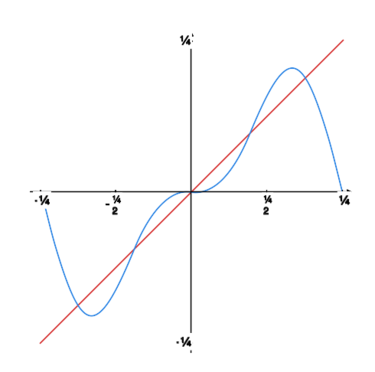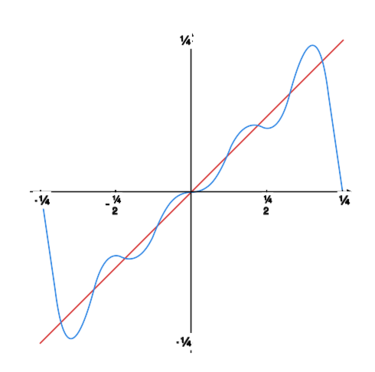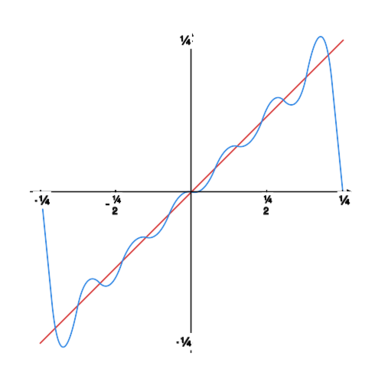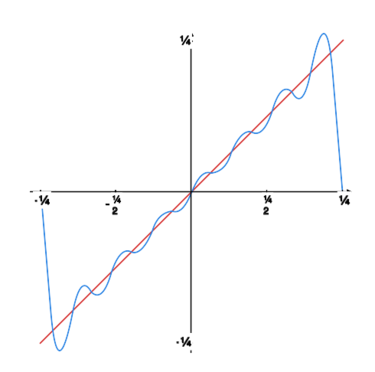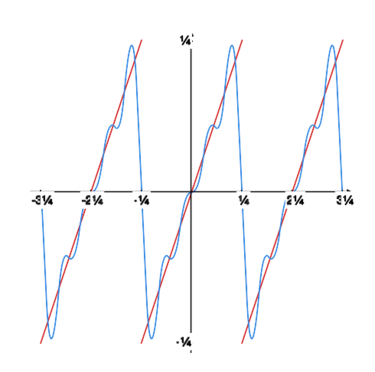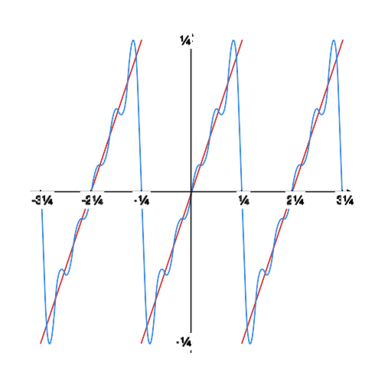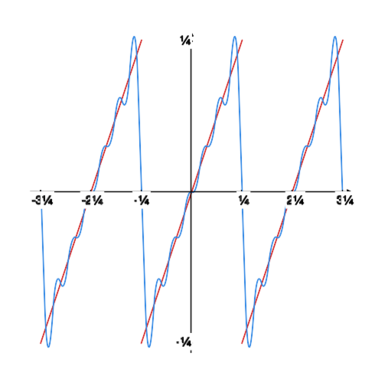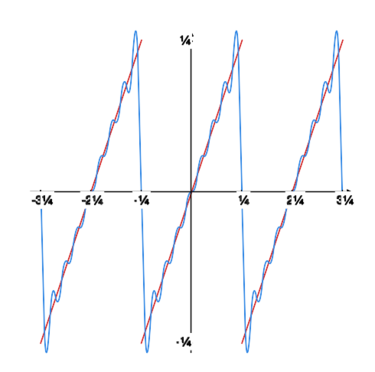Plik:Am2.M05.W.R09a.svg Aproksymacja funkcji $f(x)=x$   kolejnymi sumami szeregu Fouriera

Plik:Am2.M05.W.R09b.svg Aproksymacja funkcji $f(x)=x$   kolejnymi sumami szeregu Fouriera