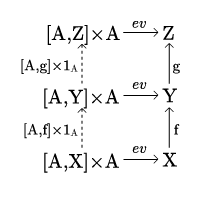Teoria kategorii dla informatyków/Ćwiczenia 4: Zaawansowane konstrukcje uniwersalne

==Zadanie 4.1==

Udowodnić, że w kategorii kartezjańsko zamkniętej $𝐂$ podnoszenie do potęgi $A \in 𝐂_{0}$ :

[A, -] : 𝐂 \to 𝐂

[A, -] (B) : = [A, B]

[A, -] (f : X \to Y) : = [A, f] : [A, X] \to [A, Y]

[A, f] : = c u r r y (f \circ e v)

gdzie $B, X, Y \in 𝐂_{0}$ , jest funktorem.

Wskazówka:

Rozwiązanie:

Ustalmy $A \in 𝐂_{0}$ . Pokażmy, że operacja $[A, -]$ zachowuje identyczności: ponieważ komutuje diagram

mamy $[A, 1_{X}] = c u r r y (1_{X} \circ e v) = 1_{[A, X]}$ , co należało pokazać. Aby pokazać, że $[A, -]$ zachowuje złożenia, rozważmy:

X \overset{f}{\to} Y \overset{g}{\to} Z

Wówczas diagram

komutuje, mamy - używając Zadania 3.6:

([A, g] \times 1_{A}) \circ ([A, f] \times 1_{A}) = ([A, g] \circ [A, f]) \times 1_{A}

Ale ponieważ strzałka $([A, g] \circ [A, f]) \times 1_{A}$ jest jedyną, która sprawia, że zewnętrzny prostokąt komutuje, musi być:

[A, g] \circ [A, f] = [A, g \circ f]

co należało pokazać.

==Zadanie 4.2==

Pokazać, że kategoria $𝐂 𝐚 𝐭$ jest kartezjańsko zamknięta.

Wskazówka:

Przypomnijmy, że obiektami $𝐂 𝐚 𝐭$ są wszystkie małe kategorie, zaś morfizmami - funktory. Należy więc najpierw przeczytać Wykład 5. dotyczący funktorów, w szczególności Zadanie 5.3.

Rozwiązanie:

Wiemy już z Wykładu 3. dotyczącego m.in. produktów, że $𝐂 𝐚 𝐭$ ma produkty. Posada też obiekt końcowy, którym jest kategoria $𝟏$ z jednym obiektem i jedną strzałką. Rzeczywiście, dla dowolnej kategorii $𝐂$ funktor stały typu $𝐂 \to 𝟏$ da się zdefiniować tylko w jeden sposób (jaki?). Dowód jest trywialny, więc go pomijamy. Aby zakończyć dowód kartezjańskiej zamkniętości $𝐂 𝐚 𝐭$ , wykażemy, że dla dowolnych dwóch kategorii $𝐀, 𝐁$ , kategoria funktorów typu $𝐀 \to 𝐁$ (z transformacjami naturalnymi jako strzałkami) jest eksponentem. Oznaczmy tę kategorię tymczasowo jako $F u n (𝐀, 𝐁)$ , gdyż po zakończeniu dowodu będziemy mogli o niej pisać $[𝐀, 𝐁]$ . Musimy zatem wykazać, że odpowiednio zdefiniowana ewaluacja jest morfizmem oraz zagwarantować istnienie bijekcji opisującej własność uniwersalną eksponentu. Oto cztery wymagane kroki:

Pokażemy, że $e v : F u n (𝐀, 𝐁) \times 𝐀 \to 𝐁$ jest funktorem. W tym celu skorzystamy z Zadania 5.3 i pokażemy, że $e v$ jest funktorem ze względu na każdą ze współrzędnych. Niech $F : 𝐀 \to 𝐁$ będzie ustalonym funktorem. Rozważmy $e v (F, -)$ . Z definicji ewaluacji dostajemy natychmiast, że $e v (F, -) = F$ , czyli jest to funktor. Jeśli $A \in 𝐀_{0}$ , to operacja $e v (-, A) : F u n (𝐀, 𝐁) \to 𝐁$ jest na strzałkach zdefiniowana następująco:

η : F \to G \mapsto η_{A} : F (A) \to G (A)

To przypisanie jest również funktorem. W końcu, prawo przemienności wymagane do założeń Zadania 4.3 jest dokładnie stwierdzeniem naturalności transformacji $η$ , a zatem zachodzi.

Niech $𝐗$ będzie dowolną kategorią, zaś $F : 𝐗 \times 𝐀 \to 𝐁$ funktorem. Wówczas $c u r r y (F) : 𝐗 \to F u n (𝐀, 𝐁)$ definiujemy jako $c u r r y (F) (X) (A) : = F (X, A)$ , gdzie $X$ może oznaczać zarówno obiekt, jak i strzałkę w $𝐗$ . Dowód, że jest to funktor, wynika wprost z definicji i faktu, że $F$ jest funktorem.
Następnie dla każdego funktora $G : 𝐗 \to F u n (𝐀, 𝐁)$ definiujemy $u n c u r r y (G) : 𝐗 \times 𝐀 \to 𝐁$ jako

u n c u r r y (G) : = e v \circ (G \times 1_{𝐀})

i pokazujemy, że jest to funktor (bo $G$ jest funktorem, identyczność $1_{𝐀} : 𝐀 \to 𝐀$ jest funktorem, produkt funktorów jest funktorem, złożenie tego z funktorem ewaluacji $e v$ też jest funktorem).

W końcu mamy $c u r r y (e v \circ (G \times 1_{𝐀})) (X) (A) = (e v \circ (G \times 1_{𝐀})) (X, A) = e v (G (X), A) = G (X) (A)$

dla $X \in 𝐗_{0}$ , $A \in 𝐀_{0}$ i dokładnie te same równości będą zachodzić na strzałkach. Dlatego

c u r r y (e v \circ (G \times 1_{𝐀})) = G

co daje szukaną bijekcję i kończy dowód.

==Zadanie 4.3==

Sprawdzić, że w dowolnej kategorii kartezjańsko zamkniętej $𝐂$ zachodzą następujące związki (gdzie trzeba, należy założyć też istnienie obiektu początkowego $𝟎$ w kategorii $𝐂$ ).

$𝟎 ≅ 𝟎 \times A$ ,
jeśli istnieje strzałka $A \to 𝟎$ , to $A ≅ 𝟎$ dla dowolnego $A \in 𝐂_{0}$ ,
jeśli $𝟎 ≅ 𝟏$ , to wszystkie obiekty $𝐂$ są izomorficzne,
dowolna strzałka $A \to 𝟎$ jest mono,
$[A, 𝟏] ≅ 𝟏$ ,
$[1, A] ≅ A$ ,
$[A \times B, C] ≅ [A, [B, C]]$ ,
$[A, B] \times [A, C] ≅ [A, B \times C]$ ,

Rozwiązanie:

Pokazujemy $𝟎 ≅ 𝟎 \times A$ . Rozważmy komutujący diagram:

z którego odczytamy - po pierwsze - że $p_{𝟎} \circ!_{𝟎 \times A} = 1_{𝟎}$ . Po drugie, widzimy, że strzałka $!_{𝟎 \times A} \circ p_{𝟎}$ sprawia, iż zewnętrzne strzałki na diagramie komutują. Ale tę samą rolę spełniłaby tu $1_{𝟎 \times A}$ . A zatem uniwersalność produktu daje nam $!_{𝟎 \times A} \circ p_{𝟎} = 1_{𝟎 \times A}$ . Wykazaliśmy więc, że $!_{𝟎 \times A}$ oraz $p_{𝟎}$ są wzajemnie odwrotnymi izomorfizmami między $𝟎$ i $𝟎 \times A$ .

Załóżmy, że istnieje strzałka $A \to 𝟎$ . Technką z punktu powyżej pokazujemy, że $A ≅ 𝟎 \times A$ dla dowolnego $A \in 𝐂_{0}$ .

A zatem złożenie $A ≅ 𝟎 \times A ≅ 𝟎$ jest szukanym izomorfizmem.

Wykażemy, że jeśli $𝟎 ≅ 𝟏$ , to wszystkie obiekty $𝐂$ są izomorficzne. Wystarczy pokazać, że przy założeniu $𝟎 ≅ 𝟏$ dowolny obiekt $A$ jest izomorficzny z obiektem końcowym, gdyż wtedy złożenie $A ≅ 𝟏 ≅ B$ da izomorfizm między dowolnymi obiektami $A, B$ . Niech $f : 𝟏 \to 𝟎$ będzie zadanym izomorfizmem. Poniższy diagram (cykl):

komutuje, więc mamy natychmiast $1_{A} = (!_{A} \circ f) \circ A$ oraz $1_{𝟏} = A \circ (!_{A} \circ f)$ , co ustanawia żądany izomorfizm $𝟏 ≅ A$ .

Dowodzimy, że dowolna strzałka $f : A \to 𝟎$ jest mono. To bardzo proste zadanie: ponieważ strzałka typu $𝟎 \to 𝟎$ jest tylko jedna, więc musi być $!_{A} \circ f = 1_{𝟎}$ . To równanie mówi, że $f$ jest sekcją, czyli w szczególności jest monomorfizmem.
Aby dowieść $[A, 𝟏] ≅ 𝟏$ , rozważmy diagram:

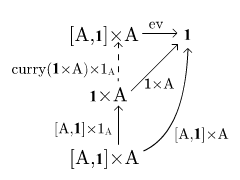
z którego wynika, że

(c u r r y (𝟏 \times A) \times 1_{A}) \circ ([A, 𝟏] \times 1_{A}) = (c u r r y (𝟏 \times A) \circ [A, 𝟏]) \times 1_{A}

jest jedyną strzałką, która sprawia, że zewnętrzna część diagramu komutuje. Zgodnie z definicją eksponentu musi zatem być:

c u r r y (𝟏 \times A) \circ [A, 𝟏] = 1_{[A, 𝟏]}

Drugi komutujący diagram

daje natychmiast:

Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1_{\mathbf{1}}\times 1_A &=& 1_{\mathbf{1}\times A}=([A,\mathbf{1}]\times 1_A)\circ (\mathrm{curry}(\mathbf{1}\times A)\times 1_A)=([A,\mathbf{1}]\circ \mathrm{curry}(\mathbf{1}\times A))\times 1_A}

skąd łatwo już wynika:

1_{𝟏} = [A, 𝟏] \circ c u r r y (𝟏 \times A)

Pokazujemy $[1, A] ≅ A$ , korzystając z wniosku z lematu Yonedy, który znajdziemy w Zadaniu 7.2. Niech $Z$ będzie dowolnym obiektem $𝐂$ . Wtedy

{H o m}_{𝐂} (Z, [𝟏, A]) ≅ {H o m}_{𝐂} (Z \times 𝟏, A) ≅ {H o m}_{𝐂} (Z, A)

gdzie wykorzystaliśmy łatwy fakt, że $Z \times 𝟏 ≅ Z$ i każdy funktor, w szczególności $H o m (-, A)$ , zachowuje izomorfizmy. Obydwa izomorfizmy powyżej są naturalne (dowód tego faktu jest łatwy lecz uciążliwy i będziemy go konsekwentnie pomijać), a zatem założenia Zadania 7.2 są spełnione. Wyciągamy wniosek, że $[𝟏, A] ≅ A$ .

Aby pokazać $[A \times B, C] ≅ [A, [B, C]]$ , niech $Z$ będzie dowolnym obiektem $𝐂$ . Wtedy

{H o m}_{𝐂} (Z, [A \times B, C]) ≅ {H o m}_{𝐂} (Z \times A \times B, C) ≅ {H o m}_{𝐂} (Z \times A, [B, C]) ≅ {H o m}_{𝐂} (Z, [A, [B, C]])

,

skąd wyciągamy wniosek, że $[A \times B, C] ≅ [A, [B, C]]$ . (To równanie dla liczb naturalnych sprowadza się do prawa potęgowania $c^{a \cdot b} = (c^{b})^{a}$ ).

Pokazujemy, że $[A, B] \times [A, C] ≅ [A, B \times C]$ : dla dowolnego $Z \in 𝐂_{0}$ mamy

{H o m}_{𝐂} (Z, [A, B] \times [A, C]) ≅ {H o m}_{𝐂} (Z, [A, B]) \times {H o m}_{𝐂} (Z, [A, C]) ≅ {H o m}_{𝐂} (Z \times A, B) \times {H o m}_{𝐂} (Z \times A, C) ≅ {H o m}_{𝐂} (Z \times A, B \times C) ≅ {H o m}_{𝐂} (Z, [A, B \times C])

Oprócz metody rozwiązania zaczerpniętej z Zadania 7.2, użyliśmy również dwukrotnie faktu, że hom-funktor zachowuje produkty, który wykazaliśmy w Zadaniu 3.5.

==Zadanie 4.4==

Udowodnij Fakt 4.5.

Rozwiązanie:

Pokażemy, że w kracie dystrybutywnej zachodzi prawo:

x \lor (y \land z) = (x \lor y) \land (x \lor z)

Rzeczywiście,

(x \lor y) \land (x \lor z) = ((x \lor y) \land x) \lor ((x \lor y) \land z) = x \lor ((x \lor y) \land z) = x \lor ((x \land z) \lor (y \land z)) = (x \lor (x \land z)) \lor (y \land z) = x \lor (y \land z)

==Zadanie 4.5==

Udowodnij Fakt 4.7.

Rozwiązanie:

Pokażemy, że w kracie dystrybutywnej element przeciwny do $x$ jest jedyny. Przypuśćmy, że $a, a^{'}$ są przeciwne do $x$ . Wówczas

a = a \lor 𝟎 = a \lor (x \land a^{'}) = (a \lor x) \land (a \lor a^{'}) = 𝟏 \land (a \lor a^{'}) = a \lor a^{'}

W ten sam sposób otrzymamy równość $a^{'} = a^{'} \lor a$ , co oznacza

a = a \lor a^{'} = a^{'} \lor a = a^{'}

==Zadanie 4.6==

Udowodnij Fakt 4.9.

Rozwiązanie:

Niech $L$ będzie dowolną algebrą Boole'a i niech $x, y, z \in L$ .

Aby pokazać $\neg (x \lor y) = \neg x \land \neg y$ zauważmy najpierw, że $𝟎 = (𝟎 \land z) \lor 𝟎$ , więc $(𝟎 \land z) \leq 𝟎$ , co daje $(𝟎 \land z) = 𝟎$ , bo $𝟎$ jest elementem najmniejszym. Dualnie dostajemy dowód $(𝟏 \lor z) = 𝟏$ . Mając dane te dwie równości, obliczamy - po pierwsze:

(x \lor y) \land (\neg x \land \neg y) = (x \land \neg x \land \neg y) \lor (y \land \neg x \land \neg y) = (𝟎 \land \neg y) \lor (𝟎 \land \neg x) = 𝟎 \lor 𝟎 = 𝟎

Po drugie:

(x \lor y) \lor (\neg x \land \neg y) = (x \lor \neg x \lor \neg y) \land (y \lor \neg x \lor \neg y) = (𝟏 \lor \neg y) \land (𝟏 \lor \neg x) = 𝟏 \land 𝟏 = 𝟏

To świadczy o tym, że $\neg x \land \neg y$ jest elementem odwrotnym do $x \lor y$ , co należało pokazać.

Dowód równości $\neg (x \land y) = \neg x \lor \neg y$ jest dualny do poprzedniego, tzn. wystarczy zaaplikować dowód poprzedni do kraty $L^{o p}$ .
Równość $\neg \neg x = x$ - proszę to zauważyć! - jest innym sformułowaniem definicji elementu przeciwnego.

==Zadanie 4.7==

Udowodnij Fakt 4.11.

Rozwiązanie:

Aby pokazać, że w dowolnej algebrze Boole'a mamy:

z \leq (\neg x \lor y) ⟺ z \land x \leq y

wykażemy zdanie równoważne, a mianowicie, że $\neg x \lor y = ⋁ A$ , gdzie $A = {z \in L ∣ z \land x \leq y}$ . Po pierwsze:

(\neg x \lor y) \land x = (\neg x \land x) \lor (y \land x) = y \land x \leq y

co daje $\neg x \lor y \in A$ . Po drugie: jeśli $z \in A$ , to $z \land x \leq y$ , co implikuje $\neg x \lor (z \land x) \leq \neg x \lor y$ . A zatem: z\leq \neg x\vee z = (\neg x\vee z)\wedge(\neg x\vee x) = \neg x\vee (z\wedge x)\leq \neg x\vee y. Pokazaliśmy zatem, że $\neg x \lor y$ jest ograniczeniem górnym zbioru $A$ . Ten element należy do $A$ , więc jest supremum $A$ .

==Zadanie 4.8==

Udowodnij Fakt 4.12.

Rozwiązanie:

Pokażemy, że w dowolnej algebrze Heytinga $L$ , jeśli dla $x \in L$ istnieje $\neg x$ , to musi być $\neg x = x \Rightarrow 𝟎$ . Załóżmy zatem, że $x$ ma element przeciwny. Skoro $\neg x \land x = 𝟎 \leq 𝟎$ , to z definicji implikacji, $\neg x \leq x \Rightarrow 𝟎$ . Aby udowodnić nierówność w przeciwną stronę, co skończy dowód, zauważmy najpierw, że $(x \Rightarrow 𝟎) \land x = 𝟎$ . A zatem:

x \Rightarrow 𝟎 = (x \Rightarrow 𝟎) \land (x \lor \neg x) = ((x \Rightarrow 𝟎) \land x) \lor ((x \Rightarrow 𝟎) \land \neg x) = 𝟎 \lor ((x \Rightarrow 𝟎) \land \neg x) = (x \Rightarrow 𝟎) \land \neg x

co oznacza przecież, że $x \Rightarrow 𝟎 \leq \neg x$ .

==Zadanie 4.9==

Udowodnij Fakt 4.13.

Rozwiązanie:

Pierwsze dwa stwierdzenia są trywialne. Równości: trzecia: $(x \Rightarrow 𝟏) = 𝟏$ , czwarta: $(𝟏 \Rightarrow x) = x$ , piąta: $(y \land z) \Rightarrow x = (z \Rightarrow (y \Rightarrow x))$ , szósta: $(x \Rightarrow (y \land z)) = (x \Rightarrow y) \land (x \Rightarrow z)$ , zostały dowiedzione dla dowolnej kategorii kartezjańsko zamkniętej w Zadaniu 4.3. Siódma nierówność $𝟏 \leq x \Rightarrow x$ jest trywialna, ósma: $𝟏 \leq (x \Rightarrow (y \Rightarrow x))$ też, pozostaje do wykazania:

𝟏 \leq (x \Rightarrow (y \Rightarrow z)) \Rightarrow ((x \Rightarrow y) \Rightarrow (x \Rightarrow z))

które to zdanie dowodzimy następująco: skoro $(y \Rightarrow z) \land y \leq z$ , to $x \Rightarrow ((y \Rightarrow z) \land y) \leq x \Rightarrow z$ , bo podnoszenie do potęgi jest funktorem - patrz Zadanie 4.1. Zadanie 4.3, część (8) daje zatem:

(x \Rightarrow (y \Rightarrow z)) \land (x \Rightarrow y) \leq x \Rightarrow z

co jest równoważne:

(x \Rightarrow (y \Rightarrow z)) \leq (x \Rightarrow y) \Rightarrow (x \Rightarrow z)

i w końcu:

𝟏 \land (x \Rightarrow (y \Rightarrow z)) \leq (x \Rightarrow y) \Rightarrow (x \Rightarrow z)

oraz:

𝟏 \leq (x \Rightarrow (y \Rightarrow z)) \Rightarrow ((x \Rightarrow y) \Rightarrow (x \Rightarrow z))

==Zadanie 4.10==

Udowodnij, że jeśli kartezjańsko zamknięta kategoria $𝐂$ ma koprodukty, to jest dystrybutywna, tzn. istnieje naturalny izomorfizm:

A \times (B + C) ≅ (A \times B) + (A \times C)

Wskazówka:

Rozwiązanie:

Znamy już metodę rozwiązania. Wystarczy nam zatem następujący ciąg izomorfizmów prawdziwy dla dowolnego $Z \in 𝐂_{0}$ :

{H o m}_{𝐂} (A \times (B + C), Z) ≅ {H o m}_{𝐂} ((B + C) \times A, Z) ≅ {H o m}_{𝐂} ((B + C), [A, Z]) ≅ {H o m}_{𝐂} (B, [A, Z]) + {H o m}_{𝐂} (C, [A, Z]) ≅ {H o m}_{𝐂} (B \times A, Z) + {H o m}_{𝐂} (C \times A, Z) ≅ {H o m}_{𝐂} (A \times B, Z) + {H o m}_{𝐂} (A \times C, Z) ≅ {H o m}_{𝐂} ((A \times B) + (A \times C), Z)

Zwróćmy uwagę, że wykorzystaliśmy tu w kluczowych momentach twierdzenie dualne do Zadania 3.5, czyli fakt, że hom-funktor ${H o m}_{𝐂} (-, Z)$ zachowuje koprodukty.

Teoria kategorii dla informatyków/Ćwiczenia 4: Zaawansowane konstrukcje uniwersalne

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia