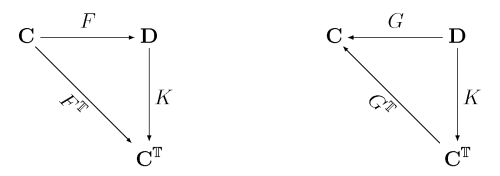Teoria kategorii dla informatyków/Ćwiczenia 11: Monady

==Zadanie 11.1==

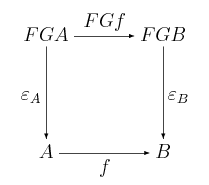
Udowodnij, że jeśli $F⊣G$ oraz $T=GF$, to naturalność $\epsilon$ implikuje, że poniższy diagram:

komutuje.

Rozwiązanie:

Niech $f:A\to B$ będzie dowolnym morfizmem w $\mathbf{𝐃}$. Naturalność $\epsilon$ wyraża się następująco:

W szczególnej sytuacji, gdy $A:=FGB$ i $f:={\epsilon }_B$ mamy:

Dla $B$ będącego w obrazie $F$, tzn. dla $B:=FC$ dla pewnego $C\in {\mathbf{𝐂}}_0$ dostajemy:

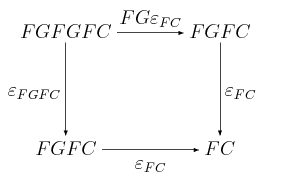
Ale $G$ jako funktor, zachowuje złożenia, więc aplikując go do ostatniego diagramu, widzimy że:

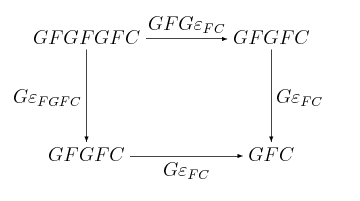
Pozbywając się nazw obiektów, podstawiając $\mu$ za $G{\epsilon }_F$ oraz $T=GF$, mamy na koniec:

==Zadanie 11.2==

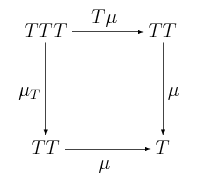
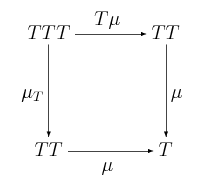
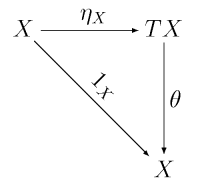
Niech $\mathbb{𝕋}=(T,\eta ,\mu )$ będzie monadą nad $\mathbf{𝐂}$. Pokaż że dla dowolnego $X\in {\mathbf{𝐂}}_0$, para $(TX,{\mu }_X)$ jest $\mathbb{𝕋}$-algebrą.

Wskazówka:

Sformułowanie zadania jest rozwiązaniem.

Rozwiązanie:

Musimy pokazać, że ${\mu }_X\circ {\eta }_{TX}=1_{TX}$, co wynika z komutowania pierwszego diagramu trójkątnego w definicji monady. Po drugie, musimy wykazać, że ${\mu }_X\circ {\mu }_{TX}={\mu }_X\circ T({\mu }_X)$, co jest również prawdą z definicji monady (diagram trzeci, prostokątny, komutuje).

==Zadanie 11.3==

Udowodnij Twierdzenie 11.2.

Wskazówka:

Definiujemy jedność sprzężenia jako $\eta$, zaś kojedność przez komponenty jako ${\epsilon }_{(X,\theta )}:=\theta$. Potem wykorzystać Twierdzenie 9.3.

Rozwiązanie:

Zauważmy, po pierwsze, że:

$G^{\mathbb{𝕋}}{F}^{\mathbb{𝕋}}=T$

a zatem mamy kandydata na jedność sprzężenia: $\eta :1_{\mathbf{𝐂}}\to G^{\mathbb{𝕋}}{F}^{\mathbb{𝕋}}$. Jak zdefiniować kojedność? Jeśli $(X,\theta )$ jest $\mathbb{𝕋}$-algebrą, to wiemy, że diagram:

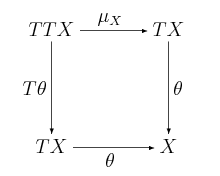
komutuje. Ale to właśnie oznacza, że $\theta$ jest morfizmem $\mathbb{𝕋}$-algebr: $\theta :(TX,{\mu }_X)\to (X,\theta )$. A zatem wolno nam zdefiniować kojedność, jak to zaproponowaliśmy we Wskazówce, jako ${\epsilon }_{(X,\theta )}:=\theta$. Pierwszy z diagramów trójkątnych z Twierdzenia 9.3 to:

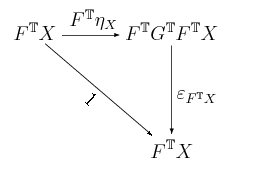
który redukuje się do znanego już komutującego diagramu: drugiego diagramu trójkątnego w definicji monady. Drugi z diagramów trójkątnych z Twierdzenia 9.3 to:

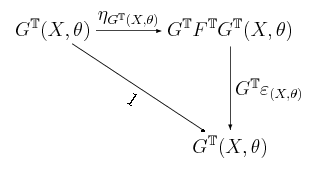
który redukuje się do znanego z definicji $\mathbb{𝕋}$-algebry komutującego diagramu:

To kończy dowód, że $F^{\mathbb{𝕋}}⊣G^{\mathbb{𝕋}}$. Indukowana monada to:

$(G^{\mathbb{𝕋}}{F}^{\mathbb{𝕋}},\eta ,G^{\mathbb{𝕋}}{\epsilon }_{{}^{\mathbb{𝕋}}})=(T,\eta ,\mu )=\mathbb{𝕋}$

==Zadanie 11.4==

Niech $\mathbb{𝕋}=(T:P\to P,1_P\le T,TT\le T)$ będzie monadą nad posetem $(P,\le )$. Pokaż, od jakiego sprzężenia pochodzi ta monada.

Wskazówka:

Wykorzystaj konstrukcję kategorii Eilenberga - Moore'a. Zauważ, że $P^{\mathbb{𝕋}}$ to poset izomorficzny z podzbiorem $P$ składającym się z punktów stałych funkcji $T$.

Rozwiązanie:

Po pierwsze, zobaczmy jak wyglądają $\mathbb{𝕋}$-algebry. Są to pary $(x,Tx\le x)$ dla $x\in P$, czyli te spośród elementów $x\in P$, dla których prawdą jest, że $Tx\le x$. Ale przecież własności monady implikują, że zawsze $x\le Tx$, a zatem $\mathbb{𝕋}$-algebry to punkty stałe funkcji $T$ .Morfizm $\mathbb{𝕋}$-algebr $(x,Tx\le x)$, $(y,Ty\le y)$ istnieje, o ile $x\le y$. A zatem $P^{\mathbb{𝕋}}$ jest częściowym porządkiem izomorficznym ze zbiorem $(\mathrm{f}\mathrm{i}\mathrm{x}(T),\le )$ (punkty stałe $T$ z porządkiem indukowanym z $P$). Funktor $G^{\mathbb{𝕋}}$, który dla prostoty oznaczymy tu $g$, można zatem interpretować jako zanurzenie $g:\mathrm{f}\mathrm{i}\mathrm{x}(T)\to P$. Funktor $F^{\mathbb{𝕋}}$, oznaczany $f$, jest funkcją monotoniczną typu $P\to \mathrm{f}\mathrm{i}\mathrm{x}(T)$, która każdemu elementowi $x\in P$ przypisuje punkt stały $Tx\in P$. Wniosek: $f$ jest obcięciem funkcji $T$ do typu $P\to \mathrm{f}\mathrm{i}\mathrm{x}(T)$. Oczywiście wtedy $fgx=x$ dla dowolnego $x\in P$. Pokażmy, że $f⊣g$, czyli dla dowolnych $a,b\in P$, $fa\le b$ wtedy i tylko wtedy, gdy $a\le gb$ w $P$. Załóżmy $fa\le b$. Wówczas z monotoniczności $g$ dostajemy $gfa\le gb$. Z definicji monady wynika, że $a\le Ta$, co czytamy też jako $a\le gfa$, co w końcu daje: $a\le gfa\le gb$. Odwrotnie, załóżmy $a\le gb$. Z monotoniczności $f$ i faktu $fg=1_P$, co zauważyliśmy w poprzednim paragrafie, mamy natychmiast: $fa\le fgb=1_{P}b=b$. To kończy dowód faktu, że: $f⊣g$.

==Zadanie 11.5==

Udowodnij, że $({𝒫},\{...\},\bigcup )$ jest monadą nad $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ dla kowariantnego funktora potęgowego ${𝒫}:\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$.

Rozwiązanie:

Pokażemy, że kolejne równania definiujące monadę są spełnione.

Niech $S\subseteq {𝒫}X$. Wówczas $({\mu }_X\circ {𝒫}{\eta }_X)(S)={\mu }_X({\eta }_X[S])=\bigcup (\{\{z\}\mid z\in S\})=S$. A zatem ${\mu }_X\circ {𝒫}{\eta }_X=1_{{𝒫}}$. Po drugie, $({\mu }_X\circ ({\eta }_{{𝒫}}{)}_X)(S)=\bigcup \{S\}=S$, co daje ${\mu }_X\circ ({\eta }_{{𝒫}}{)}_X=1_{{𝒫}}$. W końcu, niech $\alpha \subseteq {𝒫}{𝒫}X$. Wtedy $({\mu }_X\circ {𝒫}{\mu }_X)(\alpha )=\bigcup \{\bigcup W\mid W\in \alpha \}$, a z drugiej strony $({\mu }_X\circ {\mu }_{{𝒫}X})(\alpha )=\bigcup \bigcup \alpha$. Łatwa teoriomnogościowa równość $\bigcup \{\bigcup W\mid W\in \alpha \}=\bigcup \bigcup \alpha$ dowodzi zatem, że ${\mu }_X\circ {𝒫}{\mu }_X={\mu }_X\circ {\mu }_{{𝒫}X}$, co należało pokazać.

==Zadanie 11.6==

Niech $(M,*,e)$ będzie monoidem. Udowodnij, że funktor

$M\times (-):\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$

wraz z transformacjami naturalnymi ${\eta }_X(x):=(e,x)$ oraz ${\mu }_X(m_2*(m_1,x)):=(m_2*m_1,x)$ definiuje monadę $\mathbb{𝕋}$, której $\mathbb{𝕋}$-algebrami są $M$-automaty.

Rozwiązanie:

Oznaczmy $T=M\times (-)$. Jest oczywiste że $T$ jest endofunktorem na $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$. Zauważmy, że $M$-algebra to para $(X,\delta )$, gdzie $\delta :T(X)=M\times X\to X$, która spełnia dwa warunki wynikające z komutowania dwóch diagramów w definicji $M$-algebry. Te dwa równania to dokładnie te same równania, które widzieliśmy w Zadaniu 1.11! To znaczy, że $M$-algebrami są $M$-automaty.

Sprawdźmy teraz aksjomaty monady:

$\begin{array}{rlr}({\mu }_X\circ \eta )TX)(m,x)& =& {\mu }_X(e,(m,x))\\ & =& (e*m,x))\\ & =& (m,x))\\ & =& (m*e,x))\\ & =& {\mu }_X(m,(e,x))\\ & =& {\mu }_X((1_M\times {\eta }_X)(e,x))\\ & =& {\mu }_X((T{\eta }_X)(e,x))\\ & =& ({\mu }_X\circ T{\eta }_X)(e,x)),\end{array}$

co dowodzi, że $({\mu }_X\circ \eta )TX)=1_{TX}=({\mu }_X\circ T{\eta }_X)$.

Po drugie:

$\begin{array}{rlr}({\mu }_X\circ T({\mu }_X))(k,(m,(n,x)))& =& {\mu }_X(k,{\mu }_X((m,(n,x))))\\ & =& {\mu }_X(k,(m*n,x))\\ & =& (k*m*n,x))\\ & =& {\mu }_X((k*m,(n,x)))\\ & =& ({\mu }_X\circ {\mu }_{TX})(k,(m,(n,x))),\end{array}$ co pokazuje ${\mu }_X\circ T({\mu }_X)={\mu }_X\circ {\mu }_{TX}$ i kończy dowód.

==Zadanie 11.7==

Udowodnij, że funktor $(-{)}_{\mathrm{\perp }}:\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}\to {\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}}_{\mathrm{\perp }}$, który dodaje do posetu nowy element najmniejszy wraz z funktorem zapominania indukuje monadę nad $\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}$. Jakie są algebry dla tej monady?

Wskazówka:

(1) Pełna definicja dla podobnego funktora jest podana w Zadaniu 14.3. (2) ${\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}}_{\mathrm{\perp }}$ to oczywiście kategoria posetów, które posiadają element najmniejszy i funkcji monotonicznych zachowujących elementy najmniejsze.

Rozwiązanie:

Przypomnijmy, że dla funkcji monotonicznej $f:X\to Y$, $f_{\mathrm{\perp }}:X_{\mathrm{\perp }}\to Y_{\mathrm{\perp }}$ jest funkcją, która działa tak samo jak $f$ oraz zachowuje element najmniejszy, tj. $f_{\mathrm{\perp }}({\mathrm{\perp }}_X):={\mathrm{\perp }}_Y$. Oczywiście w ten sposób $(-{)}_{\mathrm{\perp }}$ jest dobrze zdefiniowanym funktorem. Jest on lewym sprzężeniem do funktora zapominania $U:Pos\to {\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}}_{\mathrm{\perp }}$, a zatem $U(-{)}_{\mathrm{\perp }}$ jest endofunktorem na $\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}$. Jednością tej monady nie może być nic innego, jak transformacja ${\eta }_X(x):=x$, zaś mnożeniem transformacja, której komponent ${\mu }_X$ jest identycznością dla elementów, które są różne od elementu najmniejszego i (dokładnie jednego) elementu bezpośrednio nad nim. Te dwa wyróżnione elementy zostają posyłane w element najmniejszy kodziedziny.

Algebra dla tej monady to para $(X,k)$, gdzie $k:U(-{)}_{\mathrm{\perp }}(X)\to X$ jest funkcją monotoniczną, która musi spełniać w szczególności $k{\eta }_X=1_X$. Funkcja $k$ jest zatem retrakcją, więc epi, więc surjekcją. W koniunkcji z drugim aksjomatem algebry dostajemy natychmiast, że $k(\mathrm{\perp })$ jest najmniejszym elementem $X$, a co za tym idzie, $k$ jest identycznością, gdy obetniemy ją do $X$.

==Zadanie 11.8==

Wykaż, że algebrami dla monady nad $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ indukowanej przez kowariantny funktor potęgowy ${𝒫}$ są półkraty zupełne i homomorfizmy tych półkrat (tzn. funkcje zachowujące dowolne suprema).

Wskazówka:

Jedynie naszkicujemy dowód.

Rozwiązanie:

Algebrą dla tej monady jest każda para $({𝒫}X,h:{𝒫}X\to X)$, która spełnia: $h(\{x\})=x$ oraz dla dowolnego $\alpha \subseteq {𝒫}X$:

$h(\{h(A)\mid A\in \alpha \})=h(\bigcup \alpha )$

Mając strukturę algebry na $X$, możemy teraz zdefiniować częściowy porządek na $X$ jako:

$x\le y⟺h(\{x,y\})=y$

Zwrotność tej relacji wynika z pierwszego z warunków na $h$. Antysymetria wynika z równości zbiorów $\{x,y\}=\{y,x\}$. Przechodniość wynika z drugiego z warunków na $h$, bo dla $x\le y$ i $y\le z$ mamy:

$h(\{x,z\})=h(\{x\}\cup \{y,z\})=h(\{x,y\}\cup \{z\})=h(\{y,z\})=z$

W tym porządku istnieją dowolne suprema dane jako $\bigvee S:=h(S)$.

Co więcej, każdy morfizm algebr jest funkcją zachowującą dowolne suprema. Te obserwacje wskazują nam funktor z ${𝒫}$-algebr w kategorię $\mathbf{𝐒}\mathbf{𝐋}\mathbf{𝐚}\mathbf{𝐭}$ półkrat. W rzeczywistości ten funktor jest częścią równoważności tych dwóch kategorii.

==Zadanie 11.9==

Wykaż, że sprzężenie $F^{\mathbb{𝕋}}⊣G^{\mathbb{𝕋}}$, od którego pochodzi monada $\mathbb{𝕋}$ jest obiektem końcowym pewnej kategorii, w następującym sensie: jeśli $F⊣G$ dla $F:\mathbf{𝐂}\to \mathbf{𝐃}:G$ jest sprzężeniem, które indukuje $\mathbb{𝕋}$, to istnieje dokładnie jeden funktor $K:\mathbf{𝐃}\to {\mathbf{𝐂}}^{\mathbb{𝕋}}$ taki, że dwa poniższe diagramy komutują:

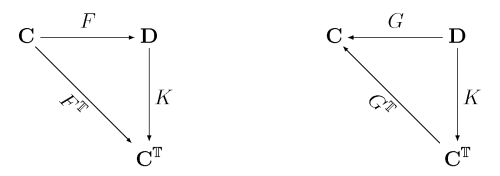
Taki funktor $K:\mathbf{𝐃}\to {\mathbf{𝐂}}^{\mathbb{𝕋}}$ nazywa się funktorem porównawczym (ang. comparison functor) dla sprzężenia $F⊣G$.

Uwaga

Dowodzi się, że sprzężenie $F^{\mathbb{𝕋}}⊣G^{\mathbb{𝕋}}$ rzeczywiście nie jest jedynym, które indukuje $\mathbb{𝕋}$, a zatem $K$ w ogólności nie trywializuje się. Okazuje się, że dla $\mathbf{𝐂}$ można skonstruować tak zwaną kategorię Kliesliego oznaczaną ${\mathbf{𝐂}}_{\mathbb{𝕋}}$, która jest w ogólności różna od ${\mathbf{𝐂}}^{\mathbb{𝕋}}$ i parę funktorów $F^{\mathbb{𝕋}}:\mathbf{𝐂}\to {\mathbf{𝐂}}_{\mathbb{𝕋}}:G_{\mathbb{𝕋}}$ z $F_{\mathbb{𝕋}}⊣G_{\mathbb{𝕋}}$, gdzie to sprzężenie indukuje $\mathbb{𝕋}$. Dalsze wiadomości na ten temat można znaleźć na przykład w podręczniku Saundersa Mac Lane'a pt. Categories for the Working Mathematician, Springer, 1997.

Wskazówka:

Największą rolę w dowodzie grają homomorfizmy algebr $K({\epsilon }_A)$ dla dowolnego $A\in {\mathbf{𝐃}}_0$.

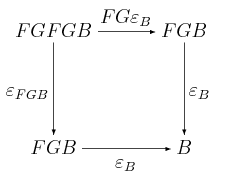
Rozwiązanie:

Przypuśćmy, że $K$ jest funktorem, który spełnia założenia zadania. Skoro drugi diagram komutuje, mamy $G^{\mathbb{𝕋}}(KX)=GX$, a zatem (bo $G^{\mathbb{𝕋}}$ jest funktorem zapominania) $KX=(GX,h_X)$ dla pewnej strzałki $h_X:GFGX=T(GX)\to GX$. Zapytajmy teraz o $F^{\mathbb{𝕋}}$, o którym informacja jest zawarta w pierwszym diagramie. Po chwili zauważamy, że:

$(GFX,h_{FX})=KFX=F^{\mathbb{𝕋}}(X)=(GFX,{\mu }_X)=(GFX,G{\epsilon }_{FX})$

co daje $h_{FX}=G{\epsilon }_{FX}$. Widzimy więc, jak strzałka $h$ jest zdefiniowana na obrazie $F$. A jak jest w ogólnym przypadku?

Niech $A\in {\mathbf{𝐃}}_0$. Skoro ${\epsilon }_A:FGA\to A$ jest strzałką w $\mathbf{𝐃}$, to strzałka $K({\epsilon }_A):K(FGA)\to K(A)$ jest z definicji funktora $K$ morfizmem $\mathbb{𝕋}$-algebr nad $\mathbf{𝐂}$. Dokładnie mówiąc, jest to morfizm pomiędzy algebrą $K(FGA)=(GFGA,h_{FGA}=G{\epsilon }_{FGA})$ a algebrą $(GA,h_A)$. To znaczy, że poniższy diagram komutuje:

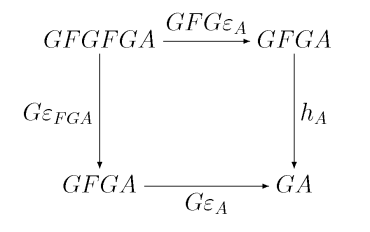
Używając faktu, że $\epsilon$ jest kojednością sprzężenia, zgodnie z Twierdzeniem 9.3, dostajemy:

$h_A=h_A\circ 1_{GFGA}=h_A\circ GFG{\epsilon }_A\circ GF{\eta }_{GA}=G{\epsilon }_A\circ G{\epsilon }_{FGA}\circ GF{\eta }_{GA}=G{\epsilon }_A\circ 1_{GA}=G{\epsilon }_A$

A zatem, jeśli $K$ istnieje, to musimy mieć:

$K(f:A\to B)=(GA,G{\epsilon }_A)\stackrel{Gf}{\to }(GB,G{\epsilon }_B)$ Łatwo sprawdzić, że ten przepis rzeczywiście definiuje funktor $K$, który spełnia zarówno równość $KF=F^{\mathbb{𝕋}}$, jak i $G^{\mathbb{𝕋}}K=G$. Gdyby istniały dwa takie funktory $K_1,K_2$, to skoro $G^{\mathbb{𝕋}}{K}_1=G=G^{\mathbb{𝕋}}{K}_2$, wierność $G^{\mathbb{𝕋}}$ implikuje $K_1=K_2$, co kończy dowód.