Analiza matematyczna 2/Wykład 4: Ciągi i szeregi funkcyjne. Szereg Taylora

Ciągi i szeregi funkcyjne. Szereg Taylora

W tym wykładzie wprowadzamy pojęcia ciągu i szeregu funkcyjnego. Rozważamy dwa rodzaje zbieżności ciągów i szeregów funkcyjnych: zbieżność punktową i jednostajną. Dowodzimy twierdzenie o ciągłości granicy jednostajnie zbieżnego ciągu funkcji ciągłych. Podajemy kryterium Weierstrassa jednostajnej zbieżności szeregu funkcyjnego. Na zakończenie wprowadzamy szereg Taylora funkcji o środku w danym punkcie (i w szczególności szereg Maclaurina).

Ten wykład jest pierwszym z dwóch wykładów poświęconych ciągom iszeregom funkcyjnym. Z szeregami liczbowymi spotkaliśmy się już na wykładzie z Analizy Matematycznej 1. Przypomnijmy, że liczbę $e$ możemy otrzymać jako sumę szeregu $\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}$. Okazuje się, że zachodzi ogólniejszy fakt

$e^x=\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}$ dla $x\in \mathbb{ℝ}$

Zapiszmy ten wzór tak

$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\dots$

Jeśli w powyższej sumie weźmiemy tylko skończoną ilość składników, to oczywiście nie dostaniemy dokładnie wartości $e^x$, niemniej dostaniemy dobre jej przybliżenie. Pozwala to nam policzyć np. $\sqrt{e}=e^{\frac{1}{2}}$ dość dokładnie jako sumę

$1+\frac{\frac{1}{2}}{1!}+\frac{\frac{1}{4}}{2!}+\frac{\frac{1}{8}}{3!}+\dots +\frac{\frac{1}{2^n}}{n!}$

(gdzie zwiększając liczbę składników, zwiększamy dokładność).

Na wykładzie zobaczymy, że wiele funkcji (przy odpowiednich założeniach) można zapisać jako sumę szeregu $f(x)=\sum _{n=0}^{\mathrm{\infty }}{f}_n(x)$, gdzie funkcje $f_n$ są na przykład jednomianami (czyli są postaci $a_n{x}^n$ jak w powyższym przykładzie z $e^x$) albo są funkcjami trygonometrycznymi (patrz szeregi Fouriera). Da nam to możliwość przybliżania funkcji $f$ przez sumę początkowych wyrazów szeregu.

Przy odpowiednich założeniach będziemy też mogli powiedzieć, czy funkcja $f$ dana jako suma szeregu jest ciągła, różniczkowalna, czy też klasy $C^{\mathrm{\infty }}$.

Ciągi funkcyjne

Plik:Am2.m04.w.r01.svg

Wykresy funkcji $f_n(x)=x^n$ dla $n=1,2,3,..$. oraz funkcji granicznej $f$

Plik:Am2.m04.w.r02.svg

Wykresy funkcji $f_n(x)=x^n$ dla $n=1,2,3,..$. oraz funkcji granicznej $f$

Definicja 4.1.

Niech $X\ne \mathrm{\varnothing }$ będzie dowolnym zbiorem oraz niech $(Y,\varrho )$ będzie przestrzenią metryczną. Niech $f:X⟶Y$ oraz $f_n:X⟶Y$ będą funkcjami dla $n\in \mathbb{\mathbb{N}}$.
(1) Mówimy, że ciąg $\{f_n\}$ jest zbieżny punktowo do funkcji $f$ i piszemy $\lim {}_{n\to +\mathrm{\infty }}{f}_n=f$ lub $f_n⟶f$, jeśli

$\mathrm{\forall }x\in X:\lim {}_{n\to +\mathrm{\infty }}{f}_n(x)=f(x)$,

co z kolei (z definicji granicy ciągu w przestrzeniach metrycznych; patrz Analiza matematyczna 1 definicja 2.2.) oznacza, że

$\mathrm{\forall }x\in X\mathrm{\forall }\epsilon >0\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N:\varrho (f_n(x),f(x))<\epsilon$

(2) Mówimy, że ciąg $\{f_n\}$ jest zbieżny jednostajnie do funkcji $f$ na zbiorze $X$ i piszemy $f_n\rightrightarrows f$, jeśli

$\mathrm{\forall }\epsilon >0\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N\mathrm{\forall }x\in X:\varrho (f_n(x),f(x))<\epsilon$

Zauważmy, że definicje zbieżności punktowej i jednostajnej różnią się tylko kolejnością kwantyfikatorów. W definicji zbieżności punktowej $N$ dobierane do $\epsilon >0$ może zmieniać się w zależności od punktu $x$. Natomiast w definicji zbieżności jednostajnej $N$ dobrane do $\epsilon >0$ nie zależy od $x$. Zatem oczywiste jest następujące twierdzenie.

Twierdzenie 4.2.

Jeśli $X\ne \mathrm{\varnothing }$ jest dowolnym zbiorem, $(Y,\varrho )$ przestrzenią metryczną, $f:X⟶Y$ oraz $f_n:X⟶Y$ funkcjami dla $n\in \mathbb{\mathbb{N}}$, to

$[f_n\rightrightarrows f⟹f_n⟶f]$

Uwaga 4.3.

Z powyższego twierdzenia wynika w szczególności, że jeśli ciąg funkcyjny $\{f_n\}$ ma granicę punktową $f$, to jeśli jest on jednostajnie zbieżny do pewnej funkcji $g$, to $f=g$. Innymi słowy jeśli ciąg $\{f_n\}$ ma granicę punktową $f$, to jedynym "kandydatem" na granicę jednostajną jest też funkcja $f$. Będzie to bardzo przydatne do badania jednostajnej zbieżności, gdyż na ogół znacznie łatwiej jest wyznaczyć granicę punktową niż granicę jednostajną. Natomiast znajomość granicy punktowej ułatwia badanie zbieżności jednostajnej (patrz uwaga poniżej).

Uwaga 4.4.

Nie jest prawdziwa implikacja odwrotna do implikacji w twierdzeniu 4.2. (czyli zbieżność punktowa nie implikuje zbieżności jednostajnej).
Aby to zobaczyć, rozważmy ciąg funkcji $\{f_n:[0,1]⟶\mathbb{ℝ}\}$ zdefiniowanych przez

$f_n(x)=x^n$ dla $x\in [0,1]$

Wyrźnie widać, że ciąg ten jest zbieżny punktowo do funkcji

$f(x)=\{\begin{array}{lll}0& \text{dla}& x\in [0,1),\\ 1& \text{dla}& x=1.\end{array}$

Pokażemy, że ciąg ten nie jest zbieżny jednostajnie do funkcji $f$. Dla dowodu niewprost przypuśćmy, że

$\mathrm{\forall }\epsilon >0\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N\mathrm{\forall }x\in [0,1]:|f_n(x)-f(x)|<\epsilon$

Weźmy teraz $\epsilon =\frac{1}{3}$. Z naszej hipotezy wynika, że

$\mathrm{\exists }{N}_1\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N_1\mathrm{\forall }x\in [0,1]:|f_n(x)-f(x)|<\epsilon =\frac{1}{3}$

Ale ponieważ $f_{N_1}(x)=x^{N_1}⟶1$, gdy $x\to 1$, zatem

$\mathrm{\exists }{x}_0\in (0,1):|f_{N_1}(x_0)-1|<\frac{1}{3}$

Zatem

$\begin{array}{rl}|f_{N_1}(x_0)-\underbrace{f(x_0)}{}_{=0}|& =|f_{N_1}(x_0)-0|=|f_{N_1}(x_0)-1+1-0|\ge |1-0|-|f_{N_1}(x_0)-1|\\ & =1-|f_{N_1}(x_0)-1|>1-\frac{1}{3}=\frac{2}{3}>\epsilon =\frac{1}{3},\end{array}$

co daje sprzeczność z wyborem $N_1$.

Uwaga 4.5.

Zobrazujmy teraz co oznacza zbieżność jednostajna $f_n\rightrightarrows f$. Otóż warunek z definicji jednostajnej zbieżności oznacza, że jeśli weźmiemy "epsilonowe otoczenie wykresu funkcji $f$", to dla odpowiednio dużych $n\ge N$ wykresy wszystkich funkcji $f_n$ będą w tym otoczeniu.
Na pierwszym rysunku mamy ciąg funkcji $f_n(x)=x^n$ dla $x\in [0,1]$. Żadna z tych funkcji nie zawiera się w epsilonowym otoczeniu wykresu funkcji granicznej (patrz uwaga 4.4.)
Z kolei poniższy rysunek przedstawia ciąg funkcji $f_n(x)=\frac{1}{n}x$ dla $x\in [0,1]$. Tutaj widać, że dla dowolnie małego $\epsilon >0$, wszystkie funkcje począwszy od pewnego $N\in \mathbb{\mathbb{N}}$ znajdą się w pasie $\mathbb{ℝ}\times (-\epsilon ,\epsilon )$, który jest otoczeniem funkcji granicznej $f\equiv 0$.

Plik:Am2.m04.w.r03.svg Ciąg funkcji $f_n(x)=x^n$ nie jest jednostajnie zbieżny na przedziale $[0,1]$

Plik:Am2.m04.w.r04.svg Ciąg funkcji $f_n(x)=nx$ jest jednostajnie zbieżny na przedziale $[0,1]$

Kolejne twierdzenie podaje ciekawą własność granicy jednostajnie zbieżnego ciągu funkcji ciągłych. Twierdzenie to ułatwi nam w niektórych przypadkach wykluczenie jednostajnej zbieżności ciągów funkcyjnych (patrz uwaga 4.4. i 4.7.).

Twierdzenie 4.6. [ciągłość granicy jednostajnie zbieżnego ciągu funkcji ciągłych]

Jeśli $(X,d_X)(Y,d_Y)$ są przestrzeniami metrycznymi, $f:X⟶Y$ oraz $f_n:X⟶Y$ są funkcjami dla $n\in \mathbb{\mathbb{N}}$, $x_0\in X$ oraz $f_n\rightrightarrows f,$
to
(1) jeśli funkcje $f_n$ są ciągłe w punkcie $x_0$, to $f$ jest funkcją ciągłą w punkcie $x_0$;
(2) jeśli funkcje $f_n$ są ciągłe, to $f$ jest funkcją ciągłą.

Dowód 4.6.

(Ad (1)) Załóżmy, że funkcje $f_n$ są ciągłe w punkcie $x_0\in X$.
Ustalmy dowolne $\epsilon >0$. Ponieważ $f_n\rightrightarrows f$, zatem

$\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N\mathrm{\forall }x\in X:d_Y(f_n(x),f(x))<\frac{\epsilon }{3}$,

w szczególności

$\mathrm{\forall }n\ge N:d_Y(f_n(x_0),f(x_0))<\frac{\epsilon }{3}$

Ponieważ funkcja $f_N$ jest ciągła w punkcie $x_0$, więc

$\mathrm{\exists }\delta >0\mathrm{\forall }x\in X:[d_X(x,x_0)<\delta ⟹d_Y(f_N(x),f_N(x_0))<\frac{\epsilon }{3}]$

Niech teraz $x\in X$ będzie taki, że $d_X(x,x_0)<\delta$. Wówczas, korzystając z nierówności trójkąta oraz trzech powyższych nierówności, mamy

$\begin{array}{lll}{d}_Y(f(x),f(x_0))& \le & d_Y(f(x),f_N(x))+d_Y(f_N(x),f_N(x_0))\\ & +& d_Y(f_N(x_0),f(x_0))<3\cdot \frac{\epsilon }{3}=\epsilon ,\end{array}$

zatem pokazaliśmy, że

$\mathrm{\forall }\epsilon >0\mathrm{\exists }\delta >0:[d_X(x,x_0)<\delta ⟹d_Y(f(x),f(x_0))<\epsilon ]$,

a to oznacza ciągłość funkcji $f$ w punkcie $x_0$.
(Ad (2)) Od razu wynika z (1).

Uwaga 4.7.

Ponieważ ciąg funkcyjny rozważany w uwadze 4.4. składał się z funkcji ciągłych oraz miał granicę nieciągłą, więc od razu z powyższego twierdzenia możemy wnioskować, że nie jest on jednostajnie zbieżny.

Kolejne twierdzenie mówi, że dla jednostajnie zbieżnego ciągu funkcji $\{f_n\}$, to samo dają dwie następujące operacje:
(1) obliczenie granicy $f$ ciągu funkcyjnego $\{f_n\}$, a następnie obliczenie granicy funkcji granicznej $f$ w punkcie $x_0$ oraz
(2) obliczenie granic poszczególnych funkcji ciągu $\{f_n\}$ w punkcie $x_0$, a następnie przejście do granicy z tak otrzymanym ciągiem liczbowym granic.
Zachodzi zatem następujący wzór:

$\underset{x\to a}{\lim }\lim {}_{n\to +\mathrm{\infty }}{f}_n(x)=\lim {}_{n\to +\mathrm{\infty }}\underset{x\to a}{\lim }{f}_n(x)$

Zwróćmy uwagę, że każdy z symboli "$\lim$" po lewej i prawej stronie oznacza co innego (raz jest to granica ciągu liczbowego, a raz granica funkcji w punkcie). Formalne sformułowanie powyższego wzoru wraz ze wszystkimi założeniami potrzebnymi do jego zachodzenia podane jest w poniższym twierdzeniu (który pozostawiamy tu bez dowodu).

Twierdzenie 4.8.

Jeśli $(X,d_X)(Y,d_Y)$ są przestrzeniami metrycznymi, przy czym przestrzeń $(Y,d_Y)$ jest zupełna, $A\subseteq X$, $f:A⟶Y$ oraz $f_n:A⟶Y$ są funkcjami dla $n\in \mathbb{\mathbb{N}}$, $f_n\rightrightarrows f,a$ jest punktem skupienia zbioru $A$ oraz

$\mathrm{\forall }n\in \mathbb{\mathbb{N}}\mathrm{\exists }\underset{x\to a}{\lim }{f}_n(x)=b_n$,

to
(1) ciąg $\{b_n\}$ jest zbieżny;
(2) $\underset{x\to a}{\lim }f(x)=\lim {}_{n\to +\mathrm{\infty }}{b}_n$.

Szeregi funkcyjne

Definicja 4.9.

Niech $A$ będzie dowolnym zbiorem oraz niech $f_n:A⟶\mathbb{ℝ}$ będą funkcjami dla $n\in \mathbb{\mathbb{N}}$.
Szeregiem $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ (lub $f_1+f_2+\dots$) nazywamy ciąg (tzw. ciąg sum częściowych) $\{F_n\}$, gdzie $F_n=\sum _{i=0}^n{f}_i$, to znaczy $F_n:A⟶\mathbb{ℝ}$, $F_n(x)=\sum _{i=0}^n{f}_i(x)$ dla $x\in A$.

Mówimy, że szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest zbieżny (punktowo) na $A$ do sumy $f:A⟶\mathbb{ℝ}$, jeśli

$F_n⟶f($ punktowo, to znaczy $F_n(x)⟶f(x)$ dla $x\in A)$

Wówczas piszemy $\sum _{n=1}^{\mathrm{\infty }}{f}_n=f$.

Mówimy, że szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest zbieżny jednostajnie na $A$ do sumy $f$, jeśli $F_n\rightrightarrows f$.

Twierdzenie 4.10.

Jeśli $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest szeregiem funkcyjnym, to

$[$ szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest zbieżny $]⟺[\mathrm{\forall }x\in A:$ szereg liczbowy $\sum _{n=1}^{\mathrm{\infty }}{f}_n(x)$ jestzbieżny $]$

Dowód 4.10.

Wynika to wprost z definicji zbieżności szeregu funkcyjnego.

Przypomnijmy, że zbieżność szeregu liczbowego jest równoważna temu, iżjego ciąg sum częściowych spełnia warunek Cauchy'ego (patrz Analiza matematyczna 1 twierdzenie 6.7.). Podobnie jest dla szeregów funkcyjnych.

Twierdzenie 4.11.

Jeśli $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest szeregiem funkcyjnym, to szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest jednostajnie zbieżny wtedy i tylko wtedy, gdy szereg spełnia warunek Cauchy'ego, to znaczy

$\begin{array}{ll}& \mathrm{\forall }\epsilon >0\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n,m\in \mathbb{\mathbb{N}}\mathrm{\forall }x\in A:\\ & \left[\right(m>n>N)⟹(|f_{n+1}(x)+\dots +f_m(x)|<\epsilon \left)\right].\end{array}$

Dowód 4.11.

"$⟹$"
Załóżmy, że szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest jednostajnie zbieżny do funkcji $f$ i oznaczmy przez $F_n$ ciąg sum częściowych tego szeregu. Ustalmy dowolne $\epsilon >0$. Z definicji jednostajnej zbieżności ciągu $\{F_n\}$ wynika, że

$\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N\mathrm{\forall }x\in A:|F_n(x)-f(x)|<\frac{\epsilon }{2}$

Zatem dla $m>n>N$ mamy

$\begin{array}{lll}|F_m(x)-F_n(x)|& =& |F_m(x)-f(x)+f(x)-F_n(x)|\\ & \le & |F_m(x)-f(x)|+|F_n(x)-f(x)|<2\cdot \frac{\epsilon }{2}=\epsilon .\end{array}$

A zatem szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ spełnia warunek Cauchy'ego.

"$⟸$"
Załóżmy teraz, że szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ spełnia warunek Cauchy'ego. Po pierwsze zauważmy, że wówczas dla dowolnego $x\in A$ szereg liczbowy $\sum _{n=1}^{\mathrm{\infty }}{f}_n(x)$ spełnia warunek Cauchy'ego dla szeregów liczbowych, a zatem jest zbieżny (patrz Analiza matematyczna 1 twierdzenie 6.7.) punktowo, powiedzmy do funkcji $f$, to znaczy $\sum _{n=1}^{\mathrm{\infty }}{f}_n(x)=f(x)$ dla $x\in A$. Pokażemy, że szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest zbieżny do $f$ jednostajnie.

Niech $\{F_n\}$ ponownie oznacza ciąg sum częściowych tego szeregu. Ustalmy dowolne $\epsilon >0$. Z warunku Cauchy'ego wiemy, że

$\begin{array}{ll}& \mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n,m\in \mathbb{\mathbb{N}}\mathrm{\forall }x\in A:\\ & \left[\right(m>n>N)⟹(|f_{n+1}(x)+\dots +f_m(x)|<\epsilon \left)\right],\end{array}$

a to oznacza, że dla $m>n>N$ oraz $x\in A$ mamy

$|F_m(x)-F_n(x)|<\epsilon$

Przejdźmy w powyższej nierówności do granicy z $m\to +\mathrm{\infty }$ (przy ustalonych $x\in A$ i $n>N$). Dostajemy

$\mathrm{\forall }x\in A\mathrm{\forall }n>N:|f(x)-F_n(x)|\le \epsilon$

A zatem ciąg $F_n\rightrightarrows f$, czyli szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest jednostajnie zbieżny do $f$, co należało dowieść.

Analogicznie jak w przypadku ciągów funkcyjnych, zbieżność jednostajna szeregów implikuje zbieżność punktową. Dowód pozostawiamy jako proste ćwiczenie.

Twierdzenie 4.12. [Zbieżność a jednostajna zbieżność]

Jeśli $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest szeregiem funkcyjnym jednostajnie zbieżnym do sumy $f$, to $\sum _{n=1}^{\mathrm{\infty }}{f}_n=f$ (to znaczy szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest zbieżny (punktowo) do sumy $f$).

Analogicznie do twierdzenia dotyczącego ciągów, dla szeregów także mamy ciągłość granicy jednostajnie zbieżnego szeregu funkcji ciągłych.

Twierdzenie 4.13. [Ciągłość granicy jednostajnie zbieżnego szeregu funkcji ciągłych]

Jeśli $A\subseteq \mathbb{ℝ}$, $x_0\in A$, $f_n:A⟶\mathbb{ℝ}$ są funkcjami dla $n\in \mathbb{\mathbb{N}}$ oraz szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest jednostajnie zbieżny do sumy $f:A⟶\mathbb{ℝ}$, to
(1) jeśli funkcje $f_n$ są ciągłe w punkcie $x_0$ dla każdego $n\in \mathbb{\mathbb{N}}$, to $f$ jest funkcją ciągłą w $x_0$;
(2) jeśli funkcje $f_n$ są ciągłe dla każdego $n\in \mathbb{\mathbb{N}}$, to $f$ jest funkcją ciągłą.

Dowód 4.13.

(Ad (1)) Załóżmy, że funkcje $f_n$ są ciągłe w punkcie $x_0$ dla każdego $n\in \mathbb{\mathbb{N}}$. Zatem także sumy częściowe $F_n=f_1+f_2+\dots +f_n$ są ciągłe w punkcie $x_0$ (patrz Analiza matematyczna 1 twierdzenie 8.9.). Zatem z twierdzenia 4.6. wnioskujemy, że granica $f=\lim {}_{n\to +\mathrm{\infty }}{F}_n$ (która istnieje z założenia) jest funkcją ciągłą.
(Ad (2)) Wynika wprost z (1).

Dla szeregów zachodzi twierdzenie analogiczne do twierdzenia 4.8.. Jeśli policzymy granicę sumy szeregu jednostajnie zbieżnego w punkcie, to otrzymamy to samo co licząc granice w punkcie dla poszczególnych wyrazów szeregu funkcyjnego, a następnie licząc sumę tak otrzymanego szeregu liczbowego. Innymi słowy, w szeregu jednostajnie zbieżnym $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ można przejść do granicy w punkcie "wyraz po wyrazie", to znaczy

$\underset{x\to a}{\lim }\sum _{n=1}^{\mathrm{\infty }}{f}_n(x)=\sum _{n=1}^{\mathrm{\infty }}\underset{x\to a}{\lim }{f}_n(x)$

Dokładne sformułowanie podane jest poniżej. Twierdzenie to możemy łatwo wykazać opierając się na twierdzenia 4.8. zastosowanym do ciągu sum częściowych szeregu.

Twierdzenie 4.14.

Jeśli $A\subseteq \mathbb{ℝ}$, $a$ jest punktem skupienia zbioru $A$, $f_n:A⟶\mathbb{ℝ}$ są funkcjami dla $n\in \mathbb{\mathbb{N}}$, szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest jednostajnie zbieżny oraz

$\mathrm{\forall }n\in \mathbb{\mathbb{N}}:\mathrm{\exists }\underset{x\to a}{\lim }{f}_n(x)=c_n\in \mathbb{ℝ}$,

to
(1) $\sum _{n=1}^{\mathrm{\infty }}{c}_n$ jest szeregiem liczbowym zbieżnym;
(2) istnieje granica $\underset{x\to a}{\lim }f(x)$ oraz $\underset{x\to a}{\lim }f(x)=\sum _{n=1}^{\mathrm{\infty }}{c}_n$.

Dla szeregów funkcyjnych podamy jedno kryterium zbieżności. Jest ono odpowiednikiem kryterium porównawczego dla szeregów liczbowych. Mówi ono, że jeśli wyrazy szeregu funkcyjnego są wspólnie ograniczone przez wyrazy szeregu liczbowego zbieżnego, to szereg ten jest jednostajnie zbieżny. Zauważmy, że kryterium to ma dość silne założenie wspólnej ograniczoności, ale za to w tezie dostajemy nie tylko zbieżność (punktową), ale aż zbieżność jednostajną.

Karl Weierstrass (1815-1897)
Zobacz biografię

Augustin Louis Cauchy (1789-1857)
Zobacz biografię

Twierdzenie 4.15. [Kryterium Weierstrassa]

Jeśli $f_n:A⟶\mathbb{ℝ}$ są funkcjami dla $n\in \mathbb{\mathbb{N}}$, szereg $\sum _{n=1}^{\mathrm{\infty }}{a}_n$ jest zbieżny oraz $\mathrm{\forall }n\in \mathbb{\mathbb{N}},x\in A:|f_n(x)|\le a_n$, to szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ jest jednostajnie zbieżny na $A$.

Dowód 4.15.

Na mocy twierdzenia 4.11. wiemy, że wystarczy pokazać zachodzenie warunku Cauchy'ego dla szeregu funkcyjnego $\sum _{n=1}^{\mathrm{\infty }}{f}_n$. W tym celu ustalmy dowolne $\epsilon >0$. Ponieważ szereg $\sum _{n=1}^{\mathrm{\infty }}{a}_n$ jest zbieżny, więc spełnia warunek Cauchy'ego zbieżności szeregów liczbowych (patrz Analiza matematyczna 1 twierdzenie 6.7.), zatem

$\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }m>n>N:a_{n+1}+\dots +a_m<\epsilon$

Zatem dla $m>n>N$ oraz dla dowolnego $x\in A$ mamy

$|f_{n+1}(x)+\dots +f_m(x)|\le |f_{n+1}(x)|+\dots +|f_m(x)|\le a_{n+1}+\dots +a_m<\epsilon$

Zatem pokazaliśmy, że szereg $\sum _{n=1}^{\mathrm{\infty }}{f}_n$ spełnia warunek Cauchy'ego zbieżności szeregów, a więcjest jednostajnie zbieżny.

W kolejnym przykładzie wykorzystamy kryterium Weierstrassa do zbadania zbieżności (jednostajnej) szeregu funkcyjnego.

Przykład 4.16.

Udowodnić zbieżność następującego szeregu funkcyjnego $\sum _{n=1}^{\mathrm{\infty }}\frac{nx}{1+n^5{x}^2}$. Pokazać, że suma jest funkcją ciągłą na $\mathbb{ℝ}$.

Aby skorzystać z kryterium Weierstrassa zbieżności szeregów, należy pokazać, że wyrazy szeregu $f_n(x)=\frac{nx}{1+n^5{x}^2}$ są ograniczone przez wyrazy pewnego zbieżnego szeregu liczbowego. Wyznaczmy ekstrema funkcji $f_n$. Obliczamy pochodne:

${f_n}^{\prime }(x)=\frac{n\cdot (1+n^5{x}^2)-nx\cdot 2n^{5}x}{(1+n^2{x}^2{)}^2}=\frac{n(1-n^5{x}^2)}{(1+n^2{x}^2{)}^2}\mathrm{\forall }n\ge 1$

Z warunku koniecznego istnienia ekstremum (zauważmy, że funkcje $f_n$ są klasy $C^{\mathrm{\infty }}$) otrzymujemy

${f_n}^{\prime }(x)=0⟺x=\pm \frac{1}{n^{\frac{5}{2}}}\mathrm{\forall }n\ge 1$

Zauważając ponadto, że $\underset{n\to \pm \mathrm{\infty }}{\lim }{f}_n(x)=0$, stwierdzamy, że funkcja $f_n$ ma ekstrema globalne w punktach $\pm \frac{1}{n^{\frac{5}{2}}}$. Zatem

$\underset{x\in \mathbb{ℝ}}{\sup }|f_n(x)|\le \left|f_n(\pm \frac{1}{n^{\frac{5}{2}}})\right|=\frac{1}{2n^{\frac{3}{2}}}\mathrm{\forall }n\ge 1$

Ponieważ szereg $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{2n^{\frac{3}{2}}}$ jest zbieżny (jako uogólniony szereg harmoniczny z wykładnikiem $\alpha =\frac{3}{2}>1$; patrz Analiza matematyczna 1 przykład 6.15.), zatem wyjściowy szereg funkcyjny jest zbieżny (i to bezwzględnie) dla każdego $x\in \mathbb{ℝ}$ oraz z kryterium Weierstrassa (patrz twierdzenie 4.15.) jest zbieżny jednostajnie w $\mathbb{ℝ}$.

Korzystając z twierdzenia o ciągłości granicy jednostajnie zbieżnego szeregu funkcji ciągłych (patrz twierdzenie 4.13.), otrzymujemy, że funkcja będąca sumą badanego

szeregu jest ciągła.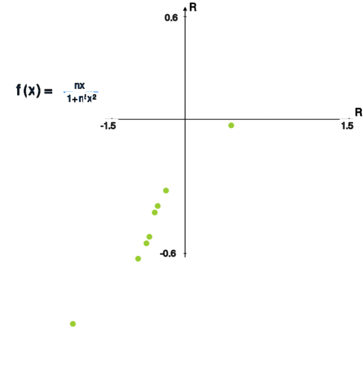

Wykresy funkcji $f_n(x)=\frac{nx}{1+n^5{x}^2}$ dla $n=1,2,3,..$.

Plik:Am2.m04.w.r06.svg Wykresy funkcji $f_n(x)=\frac{nx}{1+n^5{x}^2}$ dla $n=1,2,3,..$.

Kryterium Weierstrassa dostarcza warunku wystarczającego, ale nie koniecznego zbieżności szeregów funkcyjnych. Zostanie to pokazane w kolejnym przykładzie.

Wykres funkcji $F$

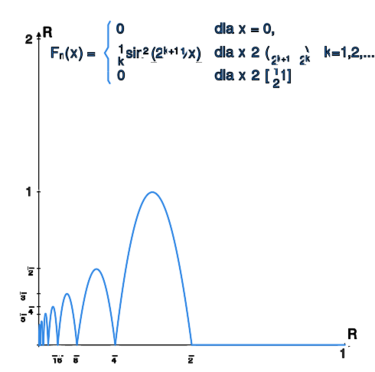
Przykład 4.17.

Pokazać jednostajną zbieżność szeregu $\sum _{n=1}^{\mathrm{\infty }}{f}_n(x)$ na przedziale $[0,1]$, gdzie

$f_n(x)=\{\begin{array}{lll}0& \text{dla}& x\in [0,\frac{1}{2^{n+1}}],\\ \\ \frac{1}{n}{\sin }^2\left(2^{n+1}\pi x\right)& \text{dla}& x\in (\frac{1}{2^{n+1}},\frac{1}{2^n}),\\ \\ 0& \text{dla}& x\in [\frac{1}{2^n},1].\\ \end{array}$

Należy zauważyć, że nie są spełnione założenia kryterium Weierstrassa.

Oznaczmy przez $\{F_n\}$ ciąg sum częściowych szeregu $\sum _{n=1}^{\mathrm{\infty }}{f}_n$. Ponieważ przedziały $(\frac{1}{2^{n+1}},\frac{1}{2^n})$ są parami rozłączne, więc

$F_n(x)=\{\begin{array}{lll}0& \text{dla}& x\in [0,\frac{1}{2^{n+1}}],\\ \\ \frac{1}{k}{\sin }^2\left(2^{k+1}\pi x\right)& \text{dla}& x\in (\frac{1}{2^{k+1}},\frac{1}{2^k}),k=1,\dots ,n,\\ \\ 0& \text{dla}& x\in [\frac{1}{2},1].\\ \end{array}$

Zatem

$F=\lim {}_{n\to +\mathrm{\infty }}{F}_n(x)=\{\begin{array}{lll}0& \text{dla}& x=0,\\ \\ \frac{1}{k}{\sin }^2\left(2^{k+1}\pi x\right)& \text{dla}& x\in (\frac{1}{2^{k+1}},\frac{1}{2^k}),k=1,2,\dots ,\\ \\ 0& \text{dla}& x\in [\frac{1}{2},1].\\ \end{array}$

Ponieważ funkcje $x⟼\frac{1}{k}{\sin }^2\left(2^{k+1}\pi x\right)$ na przedziale $(\frac{1}{2^{k+1}},\frac{1}{2^k})$ są dodatnie i przyjmują maximum w środku tego przedziału wynoszące $\frac{1}{k}$, zatem

$\underset{x\in [0,1]}{\sup }|F(x)-F_n(x)|=\frac{1}{n+1}\underset{n\to +\mathrm{\infty }}{\overset{}{\to }}0$,

więc $F_n\rightrightarrows F$ na $[0,1]$, co należało pokazać.
Zauważmy ponadto, że

$\underset{x\in [0,1]}{\sup }|f_n(x)|=\frac{1}{n}$

oraz każdy szereg $\sum _{n=1}^{\mathrm{\infty }}{c}_n$ taki, że $c_n\ge \frac{1}{n}$, jest rozbieżny z kryterium porównawczego (patrz Analiza matematyczna 1 twierdzenie 6.9.). Zatem założenia twierdzenia Weierstrassa

nie są spełnione.

Szereg Taylora

Na początek przypomnijmy twierdzenie o wzorze Taylora (patrz Analiza matematyczna 1 twierdzenie 10.9.).

Twierdzenie 4.18. [Wzór Taylora z resztą Lagrange'a]

Jeśli $I\subseteq \mathbb{ℝ}$ jest przedziałem, $f:I⟶\mathbb{ℝ}$ jest funkcją $(n+1)$-krotnie różniczkowalną, $a\in \mathrm{i}\mathrm{n}\mathrm{t}I$, to

$\mathrm{\%}\mathrm{\forall }x\in I\mathrm{\exists }\vartheta \in (0,1):f(x)=f(a)+\frac{1}{1!}{f}^{\prime }(a)(x-a)+\frac{1}{2!}{f}^{″}(a)(x-a{)}^2+\dots +\frac{1}{n!}{f}^{(n)}(a)(x-a{)}^n+R_n(x)$,

gdzie

$R_n(x)=\frac{1}{(n+1)!}{f}^{(n+1)}(a+\vartheta (x-a))(x-a{)}^{(n+1)}$

Niech $I\subseteq \mathbb{ℝ}$ oraz niech $f\in C^{\mathrm{\infty }}(I)$. Niech $a\in \mathrm{i}\mathrm{n}\mathrm{t}I$.
Możemy rozważać szereg

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n!}{f}^{(n)}(a)(x-a{)}^n$,

zwany szeregiem Taylora funkcji $f$ o środku w punkcie $a$ (umowa $f^{(0)}(x)=f(x)$).
W szczególności dla $a=0\in \mathrm{i}\mathrm{n}\mathrm{t}I$ mamy

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n!}{f}^{(n)}(0)x^n$,

Plik:Am2.m04.w.r08.svg

Aproksymacja funkcji $f(x)=e^x$ sumami szeregu Taylora

Colin Maclaurin (1698-1746)
Zobacz biografię

zwany szeregiem Maclaurina.

Z twierdzenia 4.18. (o wzorze Taylora) wynika, że warunkiem koniecznym i wystarczającym na to, by szereg Taylora był zbieżny, jest aby $R_n⟶0$, gdzie $R_n$ oznacza resztę Lagrange'a we wzorze Taylora.

Twierdzenie 4.19.

Szeregi Maclaurina funkcji: $e^x$, $\sin x$ oraz $\cos x$ są zbieżne w $\mathbb{ℝ}$, a ich sumy równe są tym funkcjom. Mówimy krótko, że funkcje te są "równe" swoim szeregom Maclaurina, czyli dla $x\in \mathbb{ℝ}$ mamy

$e^x=\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}$,

$\sin x=\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\dots =\sum _{n=1}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n+1}}{(2n+1)!}$,

$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\dots =\sum _{n=1}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n}}{(2n)!}$

Dowód 4.19.

Ponieważ wszystkie pochodne funkcji $f(x)=e^x$ wynoszą $f^{(n)}(x)=e^x$ dla $n\in \mathbb{\mathbb{N}}$, zatem wzór Maclaurina tej funkcji ma postać:

$e^x=\sum _{k=0}^n\frac{x^k}{k!}+R_n(x)$,

gdzie $R_n(x)=\frac{e^y}{(n+1)!}{y}^{n+1}$ dla pewnego $y\in [0,x]$ (lub $y\in [x,0]$, gdy $x<0$). Zatem

$|e^x-\sum _{k=0}^n\frac{x^k}{k!}|=|R_n(x)|$

Aby pokazać zbieżność szeregu Maclaurina $\sum _{k=0}^{\mathrm{\infty }}\frac{x^k}{k!}$ do funkcji $f(x)=e^x$, należy wykazać, że ciąg reszt $\{R_n(x)\}$ zmierza do zera (dla dowolnego $x\in \mathbb{ℝ}$). Mamy

$|R_n(x)|=\left|\frac{e^y}{(n+1)!}{y}^{n+1}\right|\le \frac{e^{|x|}}{(n+1)!}|x{|}^{n+1}$

Ostatnie wyrażenie przy dowolnym ustalonym $x\in \mathbb{ℝ}$ zmierza do $0$ gdy $n\to +\mathrm{\infty }$. A zatem $e^x=\sum _{k=0}^{\mathrm{\infty }}\frac{x^k}{k!}$

Dowód dla dwóch pozostałych funkcji jest analogiczny.

Plik:Am2.m04.w.r09.svg Aproksymacja funkcji $f(x)=\sin x$ sumami szeregu Taylora

Plik:Am2.m04.w.r10.svg Aproksymacja funkcji $f(x)=\cos x$ sumami szeregu Taylora

Uwaga 4.20.

Nie zawsze jednak suma szeregu Taylora funkcji klasy $C^{\mathrm{\infty }}$ jest równa tej funkcji. Przykładem takiej funkcji jest

$f(x)=\{\begin{array}{lll}{e}^{-\frac{1}{x^2}}& \text{dla}& x\ne 0,\\ 0& \text{dla}& x=0,\end{array}$

Aby to pokazać, należy obliczyć pochodne funkcji $f$ w $0$ (z definicji). Przy liczeniu granicy ilorazu różnicowego wykorzystać regułę de l'Hospitala oraz indukcję matematyczną.

Funkcje, które w pewnym otoczeniu punktu $x_0$ są równe sumie swojego szereg Taylora o środku w $x_0$ nazywamy analitycznymi.