Analiza matematyczna 2/Ćwiczenia 4: Ciągi i szeregi funkcyjne. Szereg Taylora
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Ciągi i szeregi funkcyjne. Szereg Taylora
Ćwiczenie 4.1.
Zbadać zbieżność (oraz rodzaj zbieżności) ciągów funkcyjnych:
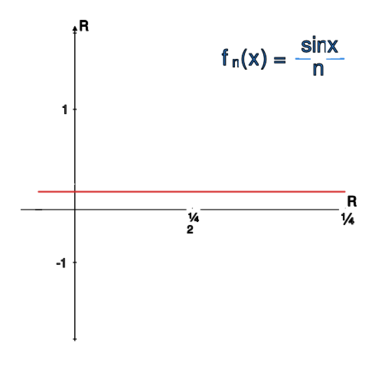
(1)
w ,
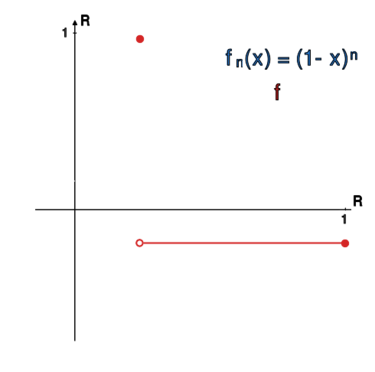
(2)
w przedziale .
Wskazówka
Rozwiązanie
Ćwiczenie 4.2.
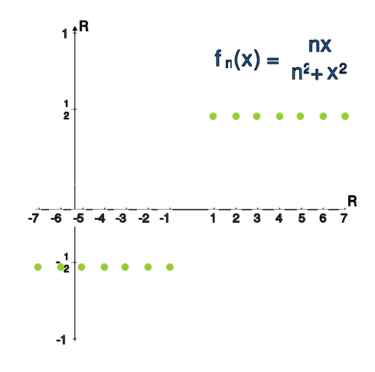
Zbadać zbieżność (oraz rodzaj zbieżności) ciągu funkcyjnego w .
Wskazówka
Rozwiązanie
Ćwiczenie 4.3.
Zbadać zbieżność (zbieżność jednostajną)
szeregu funkcyjnego w podanym obszarze:
(1)
(gdzie ,)
(2)
Wskazówka
Rozwiązanie
Ćwiczenie 4.4.
Zbadać obszar zbieżności szeregu funkcyjnego .
Wskazówka
Rozwiązanie
Ćwiczenie 4.5.
Zbadać obszar zbieżności szeregu funkcyjnego .
Wskazówka
Rozwiązanie
Ćwiczenie 4.6.
Rozwinąć w szereg Maclaurina następujące funkcje:
(1)
(2)
Wskazówka
Rozwiązanie
Ćwiczenie 4.7.
Rozwinąć funkcję w szereg Maclaurina.
Wskazówka
Rozwiązanie
Ćwiczenie 4.8.
Rozwinąć następujące funkcje w szereg Taylora o środku w punkcie :
(1)
,
(2)
.
Wskazówka
Rozwiązanie
Ćwiczenie 4.9.
Rozwinąć funkcję w szereg Taylora o środku w punkcie .
Wskazówka
Rozwiązanie