Analiza matematyczna 2/Ćwiczenia 2: Ciągi w przestrzeniach metrycznych: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „\displaystyle ” na „” |
m Zastępowanie tekstu – „\displaystyle” na „” |
||
| Linia 3: | Linia 3: | ||
{{cwiczenie|2.1.|cw_2_1| | {{cwiczenie|2.1.|cw_2_1| | ||
Niech <math> | Niech <math>(X,d)</math> będzie przestrzenią metryczną, niech | ||
<math> | <math>\{x_n\}\subseteq X</math> będzie ciągiem oraz niech <math>g\in X.</math> | ||
Udowodnić, że | Udowodnić, że | ||
jeśli <math> | jeśli <math>\lim\limits_{n\rightarrow +\infty} x_n=g</math> oraz | ||
<math> | <math>\big\{x_{n_k}\big\}</math> jest dowolnym podciągiem ciągu | ||
<math> | <math>\{x_n\},</math> to | ||
<center><math>\lim\limits_{k\rightarrow +\infty} x_{n_k} | <center><math>\lim\limits_{k\rightarrow +\infty} x_{n_k} | ||
| Linia 24: | Linia 24: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>\lim\limits_{n\rightarrow +\infty} x_n=g.</math> | ||
Należy pokazać, że <math> | Należy pokazać, że <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g.</math> | ||
Weźmy dowolne <math>\varepsilon>0.</math> | Weźmy dowolne <math>\varepsilon>0.</math> | ||
Z definicji granicy wiemy, że wszystkie | Z definicji granicy wiemy, że wszystkie | ||
wyrazy ciągu <math> | wyrazy ciągu <math>\{x_n\}</math> | ||
od pewnego miejsca leżą w kuli <math>K(g,\varepsilon).</math> | od pewnego miejsca leżą w kuli <math>K(g,\varepsilon).</math> | ||
Ale to oznacza, że także | Ale to oznacza, że także | ||
| Linia 35: | Linia 35: | ||
Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, | ||
zatem z definicji granicy | zatem z definicji granicy | ||
wnioskujemy, że <math> | wnioskujemy, że <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g.</math> | ||
</div></div> | </div></div> | ||
{{cwiczenie|2.2.|cw_2_2| | {{cwiczenie|2.2.|cw_2_2| | ||
Niech <math> | Niech <math>(X,d)</math> będzie przestrzenią metryczną, | ||
<math> | <math>\{x_n\}\subseteq X</math> ciągiem oraz niech <math>g\in X.</math> | ||
Udowodnić, że | Udowodnić, że | ||
jeśli <math> | jeśli <math>\{x_n\}</math> jest ciągiem zbieżnym oraz | ||
<math> | <math>\big\{x_{n_k}\big\}</math> jest jego dowolnym podciągiem takim, | ||
że | że | ||
<math> | <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g,</math> | ||
to także <math> | to także <math>\lim\limits_{n\rightarrow +\infty} x_n=g.</math> | ||
}} | }} | ||
| Linia 56: | Linia 56: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Z założenia wiemy, że <math> | Z założenia wiemy, że <math>\lim\limits_{n\rightarrow +\infty} x_n=g_1.</math> | ||
Z punktu (1) wynika, że także dla podciągu <math> | Z punktu (1) wynika, że także dla podciągu <math>\{x_{n_k}\}</math> | ||
mamy <math> | mamy <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g_1.</math> | ||
Z jedyności granicy | Z jedyności granicy | ||
(patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_6|twierdzenie 2.6.]]) mamy, że | (patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_6|twierdzenie 2.6.]]) mamy, że | ||
| Linia 66: | Linia 66: | ||
<span id="cw_2_3">{{cwiczenie|2.3.|| | <span id="cw_2_3">{{cwiczenie|2.3.|| | ||
Niech <math> | Niech <math>(X_i,d_i)</math> będą przestrzeniami metrycznymi dla <math>i=1,\ldots k,X=X_1\times\ldots\times X_k,\{a_n\}\subseteq X</math> ciągiem w <math>X</math> | ||
(w | (w | ||
szczególności | szczególności | ||
| Linia 73: | Linia 73: | ||
Udowodnić, że:<br> | Udowodnić, że:<br> | ||
'''(1)''' | '''(1)''' | ||
<math> | <math>\lim\limits_{n\rightarrow +\infty} a_n=a</math>, | ||
wtedy i tylko wtedy, gdy | wtedy i tylko wtedy, gdy | ||
<math> | <math>\lim\limits_{n\rightarrow +\infty} a_n^i= a^i</math> | ||
dla <math>i=1,\ldots,k.</math><br> | dla <math>i=1,\ldots,k.</math><br> | ||
<br> | <br> | ||
'''(2)''' Ciąg | '''(2)''' Ciąg | ||
<math> | <math>\{a_n\}</math> spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy | ||
ciągi <math> | ciągi <math>\{a^i_n\}</math> spełniają warunek Cauchy'ego dla <math>i=1,\ldots,k.</math> | ||
}}<span> | }}<span> | ||
| Linia 94: | Linia 94: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' | '''(1)''' | ||
"<math> | "<math>\Longrightarrow</math>":<br> | ||
Załóżmy, że <math> | Załóżmy, że <math>\lim\limits_{n\rightarrow +\infty} a_n=a.</math> | ||
Ustalmy <math>i_0\in\{1,\ldots,k\}.</math> | Ustalmy <math>i_0\in\{1,\ldots,k\}.</math> | ||
Należy pokazać, że <math> | Należy pokazać, że <math>\lim\limits_{n\rightarrow +\infty} a_n^{i_0}= a^{i_0}.</math> | ||
Ustalmy dowolne <math> | Ustalmy dowolne <math>\varepsilon>0.</math> | ||
Z definicji granicy ciągu wiemy, że | Z definicji granicy ciągu wiemy, że | ||
| Linia 123: | Linia 123: | ||
</math></center> | </math></center> | ||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
<center><math>\forall\varepsilon>0 | <center><math>\forall\varepsilon>0 | ||
| Linia 130: | Linia 130: | ||
</math></center> | </math></center> | ||
co oznacza, że <math> | co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n^{i_0}= a^{i_0}.</math><br> | ||
"<math> | "<math>\Longleftarrow</math>":<br> | ||
Załóżmy, że <math> | Załóżmy, że <math>\lim\limits_{n\rightarrow +\infty} a_n^i= a^i</math> dla każdego | ||
<math>i\in\{1,\ldots,k\}.</math> | <math>i\in\{1,\ldots,k\}.</math> | ||
Należy pokazać, że <math> | Należy pokazać, że <math>\lim\limits_{n\rightarrow +\infty} a_n=a.</math> | ||
W tym celu ustalmy dowolne <math> | W tym celu ustalmy dowolne <math>\varepsilon>0.</math> | ||
Z definicji granicy ciągu wynika, że | Z definicji granicy ciągu wynika, że | ||
| Linia 155: | Linia 155: | ||
</math></center> | </math></center> | ||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
<center><math>\forall\varepsilon>0 | <center><math>\forall\varepsilon>0 | ||
| Linia 162: | Linia 162: | ||
</math></center> | </math></center> | ||
co oznacza, że <math> | co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n= a.</math><br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
"<math> | "<math>\Longrightarrow</math>":<br> | ||
Załóżmy, że ciąg <math> | Załóżmy, że ciąg <math>\{a_n\}</math> spełnia warunek Cauchy'ego. | ||
Ustalmy <math>i_0\in\{1,\ldots,k\}.</math> | Ustalmy <math>i_0\in\{1,\ldots,k\}.</math> | ||
Należy pokazać, że ciąg <math> | Należy pokazać, że ciąg <math>\{a_n^{i_0}\}</math> | ||
spełnia warunek Cauchy'ego. | spełnia warunek Cauchy'ego. | ||
Ustalmy dowolne <math> | Ustalmy dowolne <math>\varepsilon>0.</math> | ||
Z definicji warunku Cauchy'ego wiemy, że | Z definicji warunku Cauchy'ego wiemy, że | ||
| Linia 195: | Linia 195: | ||
</math></center> | </math></center> | ||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
<center><math>\forall\varepsilon>0 | <center><math>\forall\varepsilon>0 | ||
| Linia 202: | Linia 202: | ||
</math></center> | </math></center> | ||
co oznacza, że ciąg <math> | co oznacza, że ciąg <math>\{a_n^{i_0}\}</math> | ||
spełnia warunek Cauchy'ego.<br> | spełnia warunek Cauchy'ego.<br> | ||
<br> | <br> | ||
"<math> | "<math>\Longleftarrow</math>":<br> | ||
Załóżmy, że ciąg <math> | Załóżmy, że ciąg <math>\{a_n^i\}</math> spełnia warunek Cauchy'ego dla każdego | ||
<math>i\in\{1,\ldots,k\}.</math> | <math>i\in\{1,\ldots,k\}.</math> | ||
Należy pokazać, że ciąg <math> | Należy pokazać, że ciąg <math>\{a_n\}</math> | ||
spełnia warunek Cauchy'ego. | spełnia warunek Cauchy'ego. | ||
W tym celu ustalmy dowolne <math> | W tym celu ustalmy dowolne <math>\varepsilon>0.</math> | ||
Z definicji warunku Cauchy'ego wynika, że | Z definicji warunku Cauchy'ego wynika, że | ||
| Linia 230: | Linia 230: | ||
</math></center> | </math></center> | ||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
<center><math>\forall\varepsilon>0 | <center><math>\forall\varepsilon>0 | ||
| Linia 237: | Linia 237: | ||
</math></center> | </math></center> | ||
co oznacza, że ciąg <math> | co oznacza, że ciąg <math>\{a_n\}</math> | ||
spełnia warunek Cauchy'ego. | spełnia warunek Cauchy'ego. | ||
</div></div> | </div></div> | ||
| Linia 243: | Linia 243: | ||
{{cwiczenie|2.4.|cw_2_4| | {{cwiczenie|2.4.|cw_2_4| | ||
Pokazać z definicji, że <math> | Pokazać z definicji, że <math>\mathbb{R}^2</math> (z metryką euklidesową) nie jest zbiorem | ||
zwartym. | zwartym. | ||
}} | }} | ||
| Linia 253: | Linia 253: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważmy rodzinę zbiorów otwartych | Rozważmy rodzinę zbiorów otwartych | ||
<math> | <math>\big\{K\big((0,0),n\big)\big\}_{n\in\mathbb{N}}.</math> | ||
Ponieważ | Ponieważ | ||
| Linia 261: | Linia 261: | ||
</math></center> | </math></center> | ||
zatem rodzina ta jest pokryciem zbioru <math> | zatem rodzina ta jest pokryciem zbioru <math>\mathbb{R}^2.</math> | ||
Pokażemy, że z tego pokrycia nie można wybrać podpokrycia | Pokażemy, że z tego pokrycia nie można wybrać podpokrycia | ||
skończonego. Dla dowodu niewprost przypuśćmy, że istnieje | skończonego. Dla dowodu niewprost przypuśćmy, że istnieje | ||
podpokrycie skończone | podpokrycie skończone | ||
<math> | <math>\big\{K\big((0,0),n_i\big)\big\}_{i=1}^k.</math> | ||
Zdefiniujmy <math>n_0=\max\{n_1,\ldots, n_k\}.</math> | Zdefiniujmy <math>n_0=\max\{n_1,\ldots, n_k\}.</math> | ||
Wówczas | Wówczas | ||
| Linia 276: | Linia 276: | ||
(ostatnie istotne zawieranie wynika na przykład z faktu, | (ostatnie istotne zawieranie wynika na przykład z faktu, | ||
że punkt <math> | że punkt <math>(0,n_0+1)\in\mathbb{R}^2\setminus K\big((0,0),n_0\big)</math>). | ||
Otrzymaliśmy sprzeczność. | Otrzymaliśmy sprzeczność. | ||
Zatem zbiór <math> | Zatem zbiór <math>\mathbb{R}^2</math> nie jest zwarty. | ||
</div></div> | </div></div> | ||
| Linia 299: | Linia 299: | ||
zbiór jest zwarty wtedy i tylko wtedy, gdy | zbiór jest zwarty wtedy i tylko wtedy, gdy | ||
jest skończony.<br> | jest skończony.<br> | ||
"<math> | "<math>\Longleftarrow</math>"<br> | ||
Jeśli <math>A</math> jest zbiorem skończonym, to jest zwarty | Jeśli <math>A</math> jest zbiorem skończonym, to jest zwarty | ||
(w dowolnej przestrzeni metrycznej; | (w dowolnej przestrzeni metrycznej; | ||
patrz [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_19|twierdzenia 1.19.]] (1)).<br> | patrz [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_19|twierdzenia 1.19.]] (1)).<br> | ||
"<math> | "<math>\Longrightarrow</math>"<br> | ||
Niech <math>A</math> będzie zbiorem zwartym w przestrzeni metrycznej | Niech <math>A</math> będzie zbiorem zwartym w przestrzeni metrycznej | ||
dyskretnej. | dyskretnej. | ||
| Linia 310: | Linia 310: | ||
zbiór <math>A</math> jest nieskończony. | zbiór <math>A</math> jest nieskończony. | ||
Rozważmy następującą rodzinę zbiorów otwartych | Rozważmy następującą rodzinę zbiorów otwartych | ||
<math> | <math>\{K(x,1)\}_{x\in A}.</math> | ||
Ponieważ <math>K(x,1)=\{x\}</math> zatem rodzina ta jest pokryciem | Ponieważ <math>K(x,1)=\{x\}</math> zatem rodzina ta jest pokryciem | ||
otwartym (i nieskończonym) zbioru | otwartym (i nieskończonym) zbioru | ||
| Linia 333: | Linia 333: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Ewentualnych kontrprzykładów można szukać w | Ewentualnych kontrprzykładów można szukać w | ||
<math> | <math>\mathbb{R}^2.</math> | ||
</div></div> | </div></div> | ||
| Linia 343: | Linia 343: | ||
których przecięcie <math>A\cap B</math> nie jest spójne.<br> | których przecięcie <math>A\cap B</math> nie jest spójne.<br> | ||
Suma zbiorów spójnych nie musi być zbiorem | Suma zbiorów spójnych nie musi być zbiorem | ||
spójnym. Wystarczy wziąć dwa przedziały w <math> | spójnym. Wystarczy wziąć dwa przedziały w <math>\mathbb{R}</math>: | ||
<math>A=(0,1)</math> i <math>B=(2,3)</math> (są to zbiory spójne; | <math>A=(0,1)</math> i <math>B=(2,3)</math> (są to zbiory spójne; | ||
porównaj [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_25|twierdzenia 1.25.]]). | porównaj [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_25|twierdzenia 1.25.]]). | ||
| Linia 377: | Linia 377: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Ewentualnych kontrprzykładów można szukać w | Ewentualnych kontrprzykładów można szukać w | ||
<math> | <math>\mathbb{R}.</math> | ||
</div></div> | </div></div> | ||
| Linia 387: | Linia 387: | ||
Aby to pokazać, weźmy dowolne pokrycie otwarte | Aby to pokazać, weźmy dowolne pokrycie otwarte | ||
<math> | <math>\{U_s\}_{s\in S}</math> | ||
zbioru <math>A\cup B.</math> Wówczas jest to zarówno pokrycie zbioru <math>A</math> | zbioru <math>A\cup B.</math> Wówczas jest to zarówno pokrycie zbioru <math>A</math> | ||
jak i zbioru <math>B.</math> Ponieważ zbiory <math>A</math> i <math>B</math> są zwarte, więc | jak i zbioru <math>B.</math> Ponieważ zbiory <math>A</math> i <math>B</math> są zwarte, więc | ||
możemy wybrać podpokrycia skończone | możemy wybrać podpokrycia skończone | ||
<math> | <math>\{U_{s_i}\}_{i=1}^k</math> zbioru <math>A</math> oraz | ||
<math> | <math>\{U_{s_i}\}_{i=k+1}^l</math> zbioru <math>B.</math> | ||
Wówczas <math> | Wówczas <math>\{U_{s_i}\}_{i=1}^l</math> jest pokryciem skończonym zbioru <math>A\cup B</math> | ||
(jeśli zbiór otwarty powtarza się w pierwszym i drugim podpokryciu, | (jeśli zbiór otwarty powtarza się w pierwszym i drugim podpokryciu, | ||
to bierzemy go tylko raz w <math> | to bierzemy go tylko raz w <math>\{U_{s_i}\}_{i=1}^l</math>). | ||
Jeśli zbiór <math>A\cup B</math> jest zwarty, to zbiory <math>A</math> i <math>B</math> nie | Jeśli zbiór <math>A\cup B</math> jest zwarty, to zbiory <math>A</math> i <math>B</math> nie | ||
muszą być zwarte. Jako przykład weźmy przedziały w <math> | muszą być zwarte. Jako przykład weźmy przedziały w <math>\mathbb{R}</math>: | ||
<math>A=[1,3)</math> i <math>B=(2,4].</math> Wówczas zbiory <math>A</math> i <math>B</math> nie są zwarte, | <math>A=[1,3)</math> i <math>B=(2,4].</math> Wówczas zbiory <math>A</math> i <math>B</math> nie są zwarte, | ||
ale zbiór <math>A\cup B</math> jest zwarty | ale zbiór <math>A\cup B</math> jest zwarty | ||
| Linia 411: | Linia 411: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Wziąć <math> | Wziąć <math>\varepsilon=\frac{1}{2}</math> i zastosować w definicji ciągu Cauchy'ego. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>\{x_n\}</math> będzie ciągiem Cauchy'ego przestrzeni metrycznej | ||
dyskretnej. | dyskretnej. | ||
Wówczas w szczególności dla <math> | Wówczas w szczególności dla <math>\varepsilon=\frac{1}{2}</math> mamy | ||
<center> | <center> | ||
| Linia 448: | Linia 448: | ||
{{cwiczenie|2.9.|cw_2_9| | {{cwiczenie|2.9.|cw_2_9| | ||
Rozważmy płaszczyznę <math> | Rozważmy płaszczyznę <math>\mathbb{R}^2</math> z metryką kolejową z węzłem | ||
<math>O(0,0).</math> | <math>O(0,0).</math> | ||
Zbadać zbieżność dwóch ciągów: | Zbadać zbieżność dwóch ciągów: | ||
<math> | <math>\{x_n\}</math> i <math>\{y_x\}</math> w tej metryce, gdy | ||
<math> | <math>x_n=\bigg(\frac{1}{n},1\bigg)</math> oraz | ||
<math> | <math>y_n=\bigg(0,1+\frac{1}{n}\bigg)</math> dla <math>n\in\mathbb{N}.</math> | ||
}} | }} | ||
| Linia 464: | Linia 464: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' Dla ciągu <math> | '''(1)''' Dla ciągu <math>\{x_n\}</math> zauważmy, że | ||
<center><math>\begin{array}{lll} | <center><math>\begin{array}{lll} | ||
d(x_n,x_{n+1})&=& | d(x_n,x_{n+1})&=& | ||
d_2(x_n,\Theta)+d_2(x_{n+1},\Theta)\\ | d_2(x_n,\Theta)+d_2(x_{n+1},\Theta)\\ | ||
&=& | &=& | ||
\sqrt{\bigg(\frac{1}{n}\bigg)^2+1^2} | \sqrt{\bigg(\frac{1}{n}\bigg)^2+1^2} | ||
+ | + | ||
| Linia 475: | Linia 475: | ||
\end{array}</math></center> | \end{array}</math></center> | ||
(gdzie <math> | (gdzie <math>\Theta</math> oznacza <math>((0,0)\in\mathbb{R}^2)</math>, | ||
zatem ciąg <math> | zatem ciąg <math>\{x_n\}</math> nie spełnia warunku Cauchy'ego, a zatem nie jest zbieżny.<br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
Pokażemy, że ciąg <math> | Pokażemy, że ciąg <math>\{y_n\}</math> ma granicę | ||
<math>y_0=(0,1).</math> Obliczmy | <math>y_0=(0,1).</math> Obliczmy | ||
Wersja z 10:17, 28 sie 2023
Ciągi w przestrzeniach metrycznych
Ćwiczenie 2.1.
Niech będzie przestrzenią metryczną, niech będzie ciągiem oraz niech Udowodnić, że jeśli oraz jest dowolnym podciągiem ciągu to
Ćwiczenie 2.2.
Niech będzie przestrzenią metryczną, ciągiem oraz niech Udowodnić, że jeśli jest ciągiem zbieżnym oraz jest jego dowolnym podciągiem takim, że to także
Ćwiczenie 2.3.
Niech będą przestrzeniami metrycznymi dla ciągiem w
(w
szczególności
dla
oraz ).
Udowodnić, że:
(1)
,
wtedy i tylko wtedy, gdy
dla
(2) Ciąg
spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy
ciągi spełniają warunek Cauchy'ego dla
Ćwiczenie 2.4.
Pokazać z definicji, że (z metryką euklidesową) nie jest zbiorem zwartym.
Ćwiczenie 2.5.
Jakie zbiory są zwarte w przestrzeni metrycznej dyskretnej? Odpowiedź uzasadnij.
Ćwiczenie 2.6.
Niech będzie przestrzenią metryczną
oraz Które z implikacji są prawdziwe:
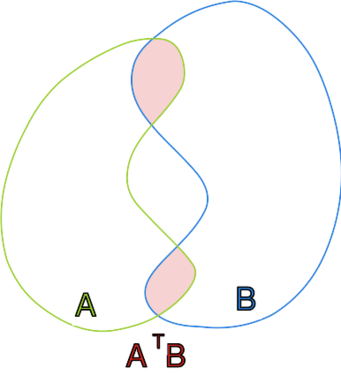
"jeśli zbiory i są spójne, to zbiór jest
spójny";
"jeśli zbiory i są spójne, to zbiór jest
spójny";
"jeśli zbiór jest spójny, to zbiory i są
spójne".
Ćwiczenie 2.7.
Niech będzie przestrzenią metryczną
oraz Które z implikacji są prawdziwe:
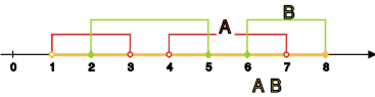
"jeśli zbiory i są zwarte, to zbiór jest
zwarty";
"jeśli zbiór jest zwarty, to zbiory i są
zwarte".
Ćwiczenie 2.8.
Opisać jak wyglądają ciągi Cauchy'ego w przestrzeni metrycznej dyskretnej.
Ćwiczenie 2.9.
Rozważmy płaszczyznę z metryką kolejową z węzłem Zbadać zbieżność dwóch ciągów: i w tej metryce, gdy oraz dla