Analiza matematyczna 2/Ćwiczenia 2: Ciągi w przestrzeniach metrycznych

Ciągi w przestrzeniach metrycznych

Ćwiczenie 2.1.

Niech $(X,d)$ będzie przestrzenią metryczną, niech $\{x_n\}\subseteq X$ będzie ciągiem oraz niech $g\in X.$ Udowodnić, że jeśli $\lim {}_{n\to +\mathrm{\infty }}{x}_n=g$ oraz $\left\{x_{n_k}\right\}$ jest dowolnym podciągiem ciągu $\{x_n\},$ to

$\lim {}_{k\to +\mathrm{\infty }}{x}_{n_k}=g.$

Wskazówka

Należy zauważyć, że zachodzenie danej własności dla od pewnego miejsca dla ciągu implikuje zachodzenie tej własności od pewnego miejsca dla podciągu.

Rozwiązanie

Niech $\lim {}_{n\to +\mathrm{\infty }}{x}_n=g.$ Należy pokazać, że $\lim {}_{k\to +\mathrm{\infty }}{x}_{n_k}=g.$ Weźmy dowolne $\epsilon >0.$ Z definicji granicy wiemy, że wszystkie wyrazy ciągu $\{x_n\}$ od pewnego miejsca leżą w kuli $K(g,\epsilon ).$ Ale to oznacza, że także wszystkie wyrazy podciągu $\{x_{n_k}\}$ od pewnego miejsca leżą w kuli $K(g,\epsilon ).$ Ponieważ $\epsilon >0$ było dowolnie wybrane, zatem z definicji granicy wnioskujemy, że $\lim {}_{k\to +\mathrm{\infty }}{x}_{n_k}=g.$

Ćwiczenie 2.2.

Niech $(X,d)$ będzie przestrzenią metryczną, $\{x_n\}\subseteq X$ ciągiem oraz niech $g\in X.$ Udowodnić, że jeśli $\{x_n\}$ jest ciągiem zbieżnym oraz $\left\{x_{n_k}\right\}$ jest jego dowolnym podciągiem takim, że $\lim {}_{k\to +\mathrm{\infty }}{x}_{n_k}=g,$ to także $\lim {}_{n\to +\mathrm{\infty }}{x}_n=g.$

Wskazówka

Skorzystać z ćwiczenia 2.1. oraz jedyność granicy (patrz twierdzenie 2.6.).

Rozwiązanie

Z założenia wiemy, że $\lim {}_{n\to +\mathrm{\infty }}{x}_n=g_1.$ Z punktu (1) wynika, że także dla podciągu $\{x_{n_k}\}$ mamy $\lim {}_{k\to +\mathrm{\infty }}{x}_{n_k}=g_1.$ Z jedyności granicy (patrz twierdzenie 2.6.) mamy, że $g=g_1,$ co należało dowieść.

Ćwiczenie 2.3.

Niech $(X_i,d_i)$ będą przestrzeniami metrycznymi dla $i=1,\dots k,X=X_1\times \dots \times X_k,\{a_n\}\subseteq X$ ciągiem w $X$ (w szczególności $a_n=(a_n^1,\dots ,a_n^k)$ dla $n\in \mathbb{\mathbb{N}}$ oraz $a=(a^1,\dots ,a^k)\in X$). Udowodnić, że:
(1) $\lim {}_{n\to +\mathrm{\infty }}{a}_n=a$, wtedy i tylko wtedy, gdy $\lim {}_{n\to +\mathrm{\infty }}{a}_n^i=a^i$ dla $i=1,\dots ,k.$

(2) Ciąg $\{a_n\}$ spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy ciągi $\{a_n^i\}$ spełniają warunek Cauchy'ego dla $i=1,\dots ,k.$

Wskazówka

(1) Należy wykorzystać definicję metryki standardowej w iloczynie kartezjańskim (patrz twierdzenie 1.15.).

(2) Dowód jest analogiczny do dowodu punktu (1).

Rozwiązanie

(1) "$⟹$":
Załóżmy, że $\lim {}_{n\to +\mathrm{\infty }}{a}_n=a.$ Ustalmy $i_0\in \{1,\dots ,k\}.$ Należy pokazać, że $\lim {}_{n\to +\mathrm{\infty }}{a}_n^{i_0}=a^{i_0}.$ Ustalmy dowolne $\epsilon >0.$ Z definicji granicy ciągu wiemy, że

$\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N:d(a_n,a)<\epsilon ,$

gdzie

$d(a_n,a)=\sqrt{d_1(a_n^1,a^1{)}^2+\dots +d_k(a_n^k,a^k{)}^2}.$

Zatem dla $n\ge N$ mamy

$d_{i_0}(a_n^{i_0},a^{i_0})\le \sqrt{d_1(a_n^1,a^1{)}^2+\dots +d_k(a_n^k,a^k{)}^2}=d(a_n,a)<\epsilon .$

Ponieważ $\epsilon >0$ było dowolnie wybrane, więc pokazaliśmy, że

$\mathrm{\forall }\epsilon >0\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N:d_{i_0}(a_n^{i_0},a^{i_0})<\epsilon ,$

co oznacza, że $\lim {}_{n\to +\mathrm{\infty }}{a}_n^{i_0}=a^{i_0}.$
"$⟸$":
Załóżmy, że $\lim {}_{n\to +\mathrm{\infty }}{a}_n^i=a^i$ dla każdego $i\in \{1,\dots ,k\}.$ Należy pokazać, że $\lim {}_{n\to +\mathrm{\infty }}{a}_n=a.$ W tym celu ustalmy dowolne $\epsilon >0.$ Z definicji granicy ciągu wynika, że

$\mathrm{\forall }i\in \{1,\dots ,k\}\mathrm{\exists }{N}_i\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N_i:d_i(a_n^i,a^i)<\frac{\epsilon }{\sqrt{k}},$

Niech $N=\max \{N_1,\dots ,N_k\}.$ Wówczas dla $n\ge N$ mamy

$d(a_n,a)=\sqrt{d_1(a_n^1,a^1{)}^2+\dots +d_k(a_n^k,a^k{)}^2}<\sqrt{k\cdot \frac{{\epsilon }^2}{k}}=\epsilon .$

Ponieważ $\epsilon >0$ było dowolnie wybrane, więc pokazaliśmy, że

$\mathrm{\forall }\epsilon >0\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n\ge N:d(a_n,a)<\epsilon ,$

co oznacza, że $\lim {}_{n\to +\mathrm{\infty }}{a}_n=a.$

(2) "$⟹$":
Załóżmy, że ciąg $\{a_n\}$ spełnia warunek Cauchy'ego. Ustalmy $i_0\in \{1,\dots ,k\}.$ Należy pokazać, że ciąg $\{a_n^{i_0}\}$ spełnia warunek Cauchy'ego. Ustalmy dowolne $\epsilon >0.$ Z definicji warunku Cauchy'ego wiemy, że

$\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n,m\ge N:d(a_n,a_m)<\epsilon ,$

gdzie

$d(a_n,a_m)=\sqrt{d_1(a_n^1,a_m^1{)}^2+\dots +d_k(a_n^k,a_m^k{)}^2}.$

Zatem dla $n,m\ge N$ mamy

$d_{i_0}(a_n^{i_0},a_m^{i_0})\le \sqrt{d_1(a_n^1,a_m^1{)}^2+\dots +d_k(a_n^k,a_m^k{)}^2}=d(a_n,a_m)<\epsilon .$

Ponieważ $\epsilon >0$ było dowolnie wybrane, więc pokazaliśmy, że

$\mathrm{\forall }\epsilon >0\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n,m\ge N:d_{i_0}(a_n^{i_0},a_m^{i_0})<\epsilon ,$

co oznacza, że ciąg $\{a_n^{i_0}\}$ spełnia warunek Cauchy'ego.

"$⟸$":
Załóżmy, że ciąg $\{a_n^i\}$ spełnia warunek Cauchy'ego dla każdego $i\in \{1,\dots ,k\}.$ Należy pokazać, że ciąg $\{a_n\}$ spełnia warunek Cauchy'ego. W tym celu ustalmy dowolne $\epsilon >0.$ Z definicji warunku Cauchy'ego wynika, że

$\mathrm{\forall }i\in \{1,\dots ,k\}\mathrm{\exists }{N}_i\in \mathbb{\mathbb{N}}\mathrm{\forall }n,m\ge N_i:d_i(a_n^i,a_m^i)<\frac{\epsilon }{\sqrt{k}}.$

Niech $N=\max \{N_1,\dots ,N_k\}.$ Wówczas dla $n,m\ge N$ mamy

$d(a_n,a_m)=\sqrt{d_1(a_n^1,a_m^1{)}^2+\dots +d_k(a_n^k,a_m^k{)}^2}<\sqrt{k\cdot \frac{{\epsilon }^2}{k}}=\epsilon .$

Ponieważ $\epsilon >0$ było dowolnie wybrane, więc pokazaliśmy, że

$\mathrm{\forall }\epsilon >0\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n,m\ge N:d(a_n,a_m)<\epsilon ,$

co oznacza, że ciąg $\{a_n\}$ spełnia warunek Cauchy'ego.

Ćwiczenie 2.4.

Pokazać z definicji, że ${\mathbb{ℝ}}^2$ (z metryką euklidesową) nie jest zbiorem zwartym.

Wskazówka

Można postępować analogicznie jak w dowodzie twierdzenia 1.22.

Rozwiązanie

Rozważmy rodzinę zbiorów otwartych $\left\{K\right((0,0),n){\}}_{n\in \mathbb{\mathbb{N}}}.$ Ponieważ

${\mathbb{ℝ}}^2=\bigcup _{n\in \mathbb{\mathbb{N}}}K((0,0),n),$

zatem rodzina ta jest pokryciem zbioru ${\mathbb{ℝ}}^2.$ Pokażemy, że z tego pokrycia nie można wybrać podpokrycia skończonego. Dla dowodu niewprost przypuśćmy, że istnieje podpokrycie skończone $\left\{K\right((0,0),n_i){\}}_{i=1}^k.$ Zdefiniujmy $n_0=\max \{n_1,\dots ,n_k\}.$ Wówczas

$\bigcup _{i=1}^{k}K((0,0),n_i)=K((0,0),n_0)⊊{\mathbb{ℝ}}^2$

(ostatnie istotne zawieranie wynika na przykład z faktu, że punkt $(0,n_0+1)\in {\mathbb{ℝ}}^2\setminus K((0,0),n_0)$). Otrzymaliśmy sprzeczność. Zatem zbiór ${\mathbb{ℝ}}^2$ nie jest zwarty.

Ćwiczenie 2.5.

Jakie zbiory są zwarte w przestrzeni metrycznej dyskretnej? Odpowiedź uzasadnij.

Wskazówka

Należy zauważyć, że zbiory jednopunktowe są otwarte (dlaczego?). Jako pokrycie otwarte rozważmy pokrycie zbiorami jednopunktowymi. Kiedy z tego pokrycia można wybrać podpokrycie skończone?

Rozwiązanie

W przestrzeni metrycznej dyskretnej zbiór jest zwarty wtedy i tylko wtedy, gdy jest skończony.
"$⟸$"
Jeśli $A$ jest zbiorem skończonym, to jest zwarty (w dowolnej przestrzeni metrycznej; patrz twierdzenia 1.19. (1)).
"$⟹$"
Niech $A$ będzie zbiorem zwartym w przestrzeni metrycznej dyskretnej. Należy pokazać, że zbiór $A$ jest skończony. Dla dowodu niewprost przypuśćmy, że zbiór $A$ jest nieskończony. Rozważmy następującą rodzinę zbiorów otwartych $\{K(x,1){\}}_{x\in A}.$ Ponieważ $K(x,1)=\{x\}$ zatem rodzina ta jest pokryciem otwartym (i nieskończonym) zbioru $A$ zbiorami jednopunktowymi. Zauważmy, że po usunięciu z tej rodziny dowolnego zbioru, przestaje ona być pokryciem zbioru $A.$ Zatem nie można z niego wybrać podpokrycia skończonego. Zatem zbiór $A$ nie jest zwarty i otrzymujemy sprzeczność.

Ćwiczenie 2.6.

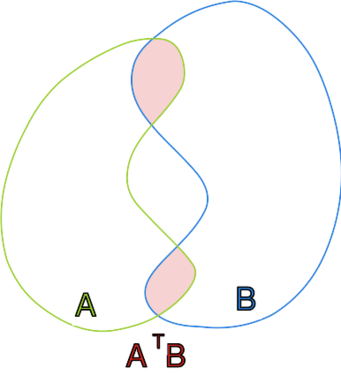
Niech $X$ będzie przestrzenią metryczną oraz $A,B\subseteq X.$ Które z implikacji są prawdziwe:
"jeśli zbiory $A$ i $B$ są spójne, to zbiór $A\cap B$ jest spójny";
"jeśli zbiory $A$ i $B$ są spójne, to zbiór $A\cup B$ jest spójny";
"jeśli zbiór $A\cup B$ jest spójny, to zbiory $A$ i $B$ są spójne".

Wskazówka

Ewentualnych kontrprzykładów można szukać w ${\mathbb{ℝ}}^2.$

Rozwiązanie

Przecięcie zbiorów spójnych nie musi być zbiorem spójnym. Rysunek przedstawia dwa zbiory spójne $A,B\subseteq {\mathbb{ℝ}}^2,$ których przecięcie $A\cap B$ nie jest spójne.
Suma zbiorów spójnych nie musi być zbiorem spójnym. Wystarczy wziąć dwa przedziały w $\mathbb{ℝ}$: $A=(0,1)$ i $B=(2,3)$ (są to zbiory spójne; porównaj twierdzenia 1.25.). Ich suma $A\cup B=(0,1)\cup (2,3)$ nie jest zbiorem spójnym, gdyż nie jest przedziałem. Oczywiście, aby zachodził kontrprzykład, zbiory $A$ i $B$ muszą być rozłączne. W przeciwnym razie z twierdzenia 1.26. wynikałoby, że suma jest zbiorem spójnym.
Jeśli zbiór $A\cup B$ jest spójny, to zbiory $A$ i $B$ nie muszą być spójne. Jako przykład weźmy zbiory $A=(1,3)\cup (4,7)$ oraz $B=[2,5]\cup [6,8].$ Wówczas zbiory $A,B\subseteq \mathbb{ℝ}$ nie są spójne, ale zbiór $A\cup B=(1,8]$ jest spójny (patrz twierdzenia 1.26.).

Przeciecie zbiorów $A$ i $B$

Suma zbiorów spójnych nie musi być zbiorem spójnym Ze spójności sumy zbiorów nie wynika spójność ich składowych

Ćwiczenie 2.7.

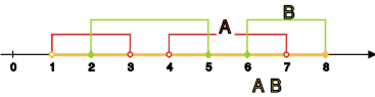
Niech $X$ będzie przestrzenią metryczną oraz $A,B\subseteq X.$ Które z implikacji są prawdziwe:
"jeśli zbiory $A$ i $B$ są zwarte, to zbiór $A\cup B$ jest zwarty";
"jeśli zbiór $A\cup B$ jest zwarty, to zbiory $A$ i $B$ są zwarte".

Wskazówka

Ewentualnych kontrprzykładów można szukać w $\mathbb{ℝ}.$

Rozwiązanie

Plik:Am2.M02.C.R04.svg

Ze zwartości sumy zbiorów nie wynika zwartość ich składowych

Jeśli zbiory $A$ i $B$ są zwarte, to zbiór $A\cup B$ jest zwarty.

Aby to pokazać, weźmy dowolne pokrycie otwarte $\{U_s{\}}_{s\in S}$ zbioru $A\cup B.$ Wówczas jest to zarówno pokrycie zbioru $A$ jak i zbioru $B.$ Ponieważ zbiory $A$ i $B$ są zwarte, więc możemy wybrać podpokrycia skończone $\{U_{s_i}{\}}_{i=1}^k$ zbioru $A$ oraz $\{U_{s_i}{\}}_{i=k+1}^l$ zbioru $B.$ Wówczas $\{U_{s_i}{\}}_{i=1}^l$ jest pokryciem skończonym zbioru $A\cup B$ (jeśli zbiór otwarty powtarza się w pierwszym i drugim podpokryciu, to bierzemy go tylko raz w $\{U_{s_i}{\}}_{i=1}^l$).

Jeśli zbiór $A\cup B$ jest zwarty, to zbiory $A$ i $B$ nie muszą być zwarte. Jako przykład weźmy przedziały w $\mathbb{ℝ}$: $A=[1,3)$ i $B=(2,4].$ Wówczas zbiory $A$ i $B$ nie są zwarte, ale zbiór $A\cup B$ jest zwarty (patrz twierdzenia 1.21.).

Ćwiczenie 2.8.

Opisać jak wyglądają ciągi Cauchy'ego w przestrzeni metrycznej dyskretnej.

Wskazówka

Wziąć $\epsilon =\frac{1}{2}$ i zastosować w definicji ciągu Cauchy'ego.

Rozwiązanie

Niech $\{x_n\}$ będzie ciągiem Cauchy'ego przestrzeni metrycznej dyskretnej. Wówczas w szczególności dla $\epsilon =\frac{1}{2}$ mamy

$\mathrm{\exists }N\in \mathbb{\mathbb{N}}\mathrm{\forall }n,m\ge N:d(x_n,x_m)<\frac{1}{2}.$

Ale metryka dyskretna przyjmuje tylko wartości $0$ i $1,$ zatem dla dowolnych $n,m\ge N$ mamy $d(x_n,x_m)=0,$ a to z kolei oznacza, że $x_n=x_m.$ Zatem pokazaliśmy, że

$\mathrm{\forall }n\ge N:x_n=x_N,$

czyli ciąg jest stały od pewnego miejsca.

Zauważmy teraz, że zachodzi także implikacja odwrotna, gdyż każdy ciąg stały jest zbieżny, więc w szczególności jest ciągiem Cauchy'ego.
Odpowiedź: W przestrzeni metrycznej dyskretnej ciąg spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy jest stały od pewnego miejsca.

Ćwiczenie 2.9.

Rozważmy płaszczyznę ${\mathbb{ℝ}}^2$ z metryką kolejową z węzłem $O(0,0).$ Zbadać zbieżność dwóch ciągów: $\{x_n\}$ i $\{y_x\}$ w tej metryce, gdy Parser nie mógł rozpoznać (nieznana funkcja „\displaystylex”): {\displaystyle \displaystylex_n=\bigg(\frac{1}{n},1\bigg)} oraz Parser nie mógł rozpoznać (nieznana funkcja „\displaystyley”): {\displaystyle \displaystyley_n=\bigg(0,1+\frac{1}{n}\bigg)} dla $n\in \mathbb{\mathbb{N}}.$

Wskazówka

Najpierw zbadać zachodzenie warunku Cauchy'ego (pozwoli to wykluczyć ciągi, które na pewno nie są zbieżne). Jeśli ciąg spełnia warunek Cauchy'ego, to spróbować znaleźć kandydata na granicę.

Rozwiązanie

(1) Dla ciągu $\{x_n\}$ zauważmy, że

$\begin{array}{lll}d(x_n,x_{n+1})& =& d_2(x_n,\mathrm{\Theta })+d_2(x_{n+1},\mathrm{\Theta })\\ & =& \sqrt{(\frac{1}{n}{)}^2+1^2}+\sqrt{(\frac{1}{n+1}{)}^2+1^2}\ge 2,\end{array}$

(gdzie $\mathrm{\Theta }$ oznacza $((0,0)\in {\mathbb{ℝ}}^2)$,

zatem ciąg $\{x_n\}$ nie spełnia warunku Cauchy'ego, a zatem nie jest zbieżny.

(2) Pokażemy, że ciąg $\{y_n\}$ ma granicę $y_0=(0,1).$ Obliczmy

$d(y_n,y_0)=d(y_n,y_0)=\sqrt{0^2+(1+\frac{1}{n}-1)}=\frac{1}{n},$

zatem $d(y_n,y_0)⟶0$, gdy $n\to +\mathrm{\infty },$ a to oznacza, że $y_n\underset{d}{\overset{}{\to }}{y}_0=(1,0).$