Analiza matematyczna 2/Ćwiczenia 2: Ciągi w przestrzeniach metrycznych: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „\displaystyle” na „” |
|||
| Linia 12: | Linia 12: | ||
<center><math>\lim\limits_{k\rightarrow +\infty} x_{n_k} | <center><math>\lim\limits_{k\rightarrow +\infty} x_{n_k} | ||
= | = | ||
g | g | ||
</math></center> | </math></center> | ||
| Linia 24: | Linia 24: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math>\lim\limits_{n\rightarrow +\infty} x_n=g | Niech <math>\lim\limits_{n\rightarrow +\infty} x_n=g</math> | ||
Należy pokazać, że <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g | Należy pokazać, że <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g</math> | ||
Weźmy dowolne <math>\varepsilon>0 | Weźmy dowolne <math>\varepsilon>0</math> | ||
Z definicji granicy wiemy, że wszystkie | Z definicji granicy wiemy, że wszystkie | ||
wyrazy ciągu <math>\{x_n\}</math> | wyrazy ciągu <math>\{x_n\}</math> | ||
od pewnego miejsca leżą w kuli <math>K(g,\varepsilon) | od pewnego miejsca leżą w kuli <math>K(g,\varepsilon)</math> | ||
Ale to oznacza, że także | Ale to oznacza, że także | ||
wszystkie wyrazy podciągu <math>\{x_{n_k}\}</math> od pewnego miejsca leżą w | wszystkie wyrazy podciągu <math>\{x_{n_k}\}</math> od pewnego miejsca leżą w | ||
kuli <math>K(g,\varepsilon) | kuli <math>K(g,\varepsilon)</math> | ||
Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, | ||
zatem z definicji granicy | zatem z definicji granicy | ||
wnioskujemy, że <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g | wnioskujemy, że <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g</math> | ||
</div></div> | </div></div> | ||
| Linia 41: | Linia 41: | ||
Niech <math>(X,d)</math> będzie przestrzenią metryczną, | Niech <math>(X,d)</math> będzie przestrzenią metryczną, | ||
<math>\{x_n\}\subseteq X</math> ciągiem oraz niech <math>g\in X | <math>\{x_n\}\subseteq X</math> ciągiem oraz niech <math>g\in X</math> | ||
Udowodnić, że | Udowodnić, że | ||
jeśli <math>\{x_n\}</math> jest ciągiem zbieżnym oraz | jeśli <math>\{x_n\}</math> jest ciągiem zbieżnym oraz | ||
<math>\big\{x_{n_k}\big\}</math> jest jego dowolnym podciągiem takim, | <math>\big\{x_{n_k}\big\}</math> jest jego dowolnym podciągiem takim, | ||
że | że | ||
<math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g | <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g</math> | ||
to także <math>\lim\limits_{n\rightarrow +\infty} x_n=g | to także <math>\lim\limits_{n\rightarrow +\infty} x_n=g</math> | ||
}} | }} | ||
| Linia 56: | Linia 56: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Z założenia wiemy, że <math>\lim\limits_{n\rightarrow +\infty} x_n=g_1 | Z założenia wiemy, że <math>\lim\limits_{n\rightarrow +\infty} x_n=g_1</math> | ||
Z punktu (1) wynika, że także dla podciągu <math>\{x_{n_k}\}</math> | Z punktu (1) wynika, że także dla podciągu <math>\{x_{n_k}\}</math> | ||
mamy <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g_1 | mamy <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g_1</math> | ||
Z jedyności granicy | Z jedyności granicy | ||
(patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_6|twierdzenie 2.6.]]) mamy, że | (patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_6|twierdzenie 2.6.]]) mamy, że | ||
| Linia 80: | Linia 80: | ||
'''(2)''' Ciąg | '''(2)''' Ciąg | ||
<math>\{a_n\}</math> spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy | <math>\{a_n\}</math> spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy | ||
ciągi <math>\{a^i_n\}</math> spełniają warunek Cauchy'ego dla <math>i=1,\ldots,k | ciągi <math>\{a^i_n\}</math> spełniają warunek Cauchy'ego dla <math>i=1,\ldots,k</math> | ||
}}<span> | }}<span> | ||
| Linia 95: | Linia 95: | ||
'''(1)''' | '''(1)''' | ||
"<math>\Longrightarrow</math>":<br> | "<math>\Longrightarrow</math>":<br> | ||
Załóżmy, że <math>\lim\limits_{n\rightarrow +\infty} a_n=a | Załóżmy, że <math>\lim\limits_{n\rightarrow +\infty} a_n=a</math> | ||
Ustalmy <math>i_0\in\{1,\ldots,k\}.</math> | Ustalmy <math>i_0\in\{1,\ldots,k\}.</math> | ||
Należy pokazać, że <math>\lim\limits_{n\rightarrow +\infty} a_n^{i_0}= a^{i_0} | Należy pokazać, że <math>\lim\limits_{n\rightarrow +\infty} a_n^{i_0}= a^{i_0}</math> | ||
Ustalmy dowolne <math>\varepsilon>0 | Ustalmy dowolne <math>\varepsilon>0</math> | ||
Z definicji granicy ciągu wiemy, że | Z definicji granicy ciągu wiemy, że | ||
| Linia 109: | Linia 109: | ||
<center><math>d(a_n,a) | <center><math>d(a_n,a) | ||
= | = | ||
\sqrt{d_1(a_n^1,a^1)^2+\ldots+d_k(a_n^k,a^k)^2} | \sqrt{d_1(a_n^1,a^1)^2+\ldots+d_k(a_n^k,a^k)^2} | ||
</math></center> | </math></center> | ||
| Linia 127: | Linia 127: | ||
<center><math>\forall\varepsilon>0 | <center><math>\forall\varepsilon>0 | ||
\exists N\in\mathbb{N}\ \forall n\ge N: | \exists N\in\mathbb{N}\ \forall n\ge N: | ||
d_{i_0}(a_n^{i_0},a^{i_0})<\varepsilon | d_{i_0}(a_n^{i_0},a^{i_0})<\varepsilon | ||
</math></center> | </math></center> | ||
co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n^{i_0}= a^{i_0} | co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n^{i_0}= a^{i_0}</math><br> | ||
"<math>\Longleftarrow</math>":<br> | "<math>\Longleftarrow</math>":<br> | ||
Załóżmy, że <math>\lim\limits_{n\rightarrow +\infty} a_n^i= a^i</math> dla każdego | Załóżmy, że <math>\lim\limits_{n\rightarrow +\infty} a_n^i= a^i</math> dla każdego | ||
<math>i\in\{1,\ldots,k\}.</math> | <math>i\in\{1,\ldots,k\}.</math> | ||
Należy pokazać, że <math>\lim\limits_{n\rightarrow +\infty} a_n=a | Należy pokazać, że <math>\lim\limits_{n\rightarrow +\infty} a_n=a</math> | ||
W tym celu ustalmy dowolne <math>\varepsilon>0.</math> | W tym celu ustalmy dowolne <math>\varepsilon>0.</math> | ||
Z definicji granicy ciągu wynika, że | Z definicji granicy ciągu wynika, że | ||
| Linia 140: | Linia 140: | ||
<center><math>\forall i\in\{1,\ldots,k\} | <center><math>\forall i\in\{1,\ldots,k\} | ||
\exists N_i\in\mathbb{N}\ \forall n\ge N_i: | \exists N_i\in\mathbb{N}\ \forall n\ge N_i: | ||
d_i(a_n^i,a^i)<\frac{\varepsilon}{\sqrt{k}} | d_i(a_n^i,a^i)<\frac{\varepsilon}{\sqrt{k}} | ||
</math></center> | </math></center> | ||
Niech <math>N=\max\{N_1,\ldots,N_k\} | Niech <math>N=\max\{N_1,\ldots,N_k\}</math> | ||
Wówczas dla <math>n\ge N</math> mamy | Wówczas dla <math>n\ge N</math> mamy | ||
| Linia 162: | Linia 162: | ||
</math></center> | </math></center> | ||
co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n= a | co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n= a</math><br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
"<math>\Longrightarrow</math>":<br> | "<math>\Longrightarrow</math>":<br> | ||
Załóżmy, że ciąg <math>\{a_n\}</math> spełnia warunek Cauchy'ego. | Załóżmy, że ciąg <math>\{a_n\}</math> spełnia warunek Cauchy'ego. | ||
Ustalmy <math>i_0\in\{1,\ldots,k\} | Ustalmy <math>i_0\in\{1,\ldots,k\}</math> | ||
Należy pokazać, że ciąg <math>\{a_n^{i_0}\}</math> | Należy pokazać, że ciąg <math>\{a_n^{i_0}\}</math> | ||
spełnia warunek Cauchy'ego. | spełnia warunek Cauchy'ego. | ||
Ustalmy dowolne <math>\varepsilon>0 | Ustalmy dowolne <math>\varepsilon>0</math> | ||
Z definicji warunku Cauchy'ego wiemy, że | Z definicji warunku Cauchy'ego wiemy, że | ||
<center><math>\exists N\in\mathbb{N}\ \forall n,m\ge N: | <center><math>\exists N\in\mathbb{N}\ \forall n,m\ge N: | ||
d(a_n,a_m)<\varepsilon | d(a_n,a_m)<\varepsilon | ||
</math></center> | </math></center> | ||
| Linia 181: | Linia 181: | ||
<center><math>d(a_n,a_m) | <center><math>d(a_n,a_m) | ||
= | = | ||
\sqrt{d_1(a_n^1,a_m^1)^2+\ldots+d_k(a_n^k,a_m^k)^2} | \sqrt{d_1(a_n^1,a_m^1)^2+\ldots+d_k(a_n^k,a_m^k)^2} | ||
</math></center> | </math></center> | ||
| Linia 199: | Linia 199: | ||
<center><math>\forall\varepsilon>0 | <center><math>\forall\varepsilon>0 | ||
\exists N\in\mathbb{N}\ \forall n,m\ge N: | \exists N\in\mathbb{N}\ \forall n,m\ge N: | ||
d_{i_0}(a_n^{i_0},a_m^{i_0})<\varepsilon | d_{i_0}(a_n^{i_0},a_m^{i_0})<\varepsilon | ||
</math></center> | </math></center> | ||
| Linia 210: | Linia 210: | ||
Należy pokazać, że ciąg <math>\{a_n\}</math> | Należy pokazać, że ciąg <math>\{a_n\}</math> | ||
spełnia warunek Cauchy'ego. | spełnia warunek Cauchy'ego. | ||
W tym celu ustalmy dowolne <math>\varepsilon>0 | W tym celu ustalmy dowolne <math>\varepsilon>0</math> | ||
Z definicji warunku Cauchy'ego wynika, że | Z definicji warunku Cauchy'ego wynika, że | ||
<center><math>\forall i\in\{1,\ldots,k\} | <center><math>\forall i\in\{1,\ldots,k\} | ||
\exists N_i\in\mathbb{N}\ \forall n,m\ge N_i: | \exists N_i\in\mathbb{N}\ \forall n,m\ge N_i: | ||
d_i(a_n^i,a_m^i)<\frac{\varepsilon}{\sqrt{k}} | d_i(a_n^i,a_m^i)<\frac{\varepsilon}{\sqrt{k}} | ||
</math></center> | </math></center> | ||
Niech <math>N=\max\{N_1,\ldots,N_k\} | Niech <math>N=\max\{N_1,\ldots,N_k\}</math> | ||
Wówczas dla <math>n,m\ge N</math> mamy | Wówczas dla <math>n,m\ge N</math> mamy | ||
| Linia 234: | Linia 234: | ||
<center><math>\forall\varepsilon>0 | <center><math>\forall\varepsilon>0 | ||
\exists N\in\mathbb{N}\ \forall n,m\ge N: | \exists N\in\mathbb{N}\ \forall n,m\ge N: | ||
d(a_n,a_m)<\varepsilon | d(a_n,a_m)<\varepsilon | ||
</math></center> | </math></center> | ||
| Linia 253: | Linia 253: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważmy rodzinę zbiorów otwartych | Rozważmy rodzinę zbiorów otwartych | ||
<math>\big\{K\big((0,0),n\big)\big\}_{n\in\mathbb{N}} | <math>\big\{K\big((0,0),n\big)\big\}_{n\in\mathbb{N}}</math> | ||
Ponieważ | Ponieważ | ||
<center><math>\mathbb{R}^2 | <center><math>\mathbb{R}^2 | ||
= | = | ||
\bigcup_{n\in\mathbb{N}} K\big((0,0),n\big) | \bigcup_{n\in\mathbb{N}} K\big((0,0),n\big) | ||
</math></center> | </math></center> | ||
zatem rodzina ta jest pokryciem zbioru <math>\mathbb{R}^2 | zatem rodzina ta jest pokryciem zbioru <math>\mathbb{R}^2</math> | ||
Pokażemy, że z tego pokrycia nie można wybrać podpokrycia | Pokażemy, że z tego pokrycia nie można wybrać podpokrycia | ||
skończonego. Dla dowodu niewprost przypuśćmy, że istnieje | skończonego. Dla dowodu niewprost przypuśćmy, że istnieje | ||
podpokrycie skończone | podpokrycie skończone | ||
<math>\big\{K\big((0,0),n_i\big)\big\}_{i=1}^k | <math>\big\{K\big((0,0),n_i\big)\big\}_{i=1}^k</math> | ||
Zdefiniujmy <math>n_0=\max\{n_1,\ldots, n_k\} | Zdefiniujmy <math>n_0=\max\{n_1,\ldots, n_k\}</math> | ||
Wówczas | Wówczas | ||
| Linia 276: | Linia 276: | ||
(ostatnie istotne zawieranie wynika na przykład z faktu, | (ostatnie istotne zawieranie wynika na przykład z faktu, | ||
że punkt <math>(0,n_0+1)\in\mathbb{R}^2\setminus K\big((0,0),n_0\big)</math>) | że punkt <math>(0,n_0+1)\in\mathbb{R}^2\setminus K\big((0,0),n_0\big)</math>) | ||
Otrzymaliśmy sprzeczność. | Otrzymaliśmy sprzeczność. | ||
Zatem zbiór <math>\mathbb{R}^2</math> nie jest zwarty. | Zatem zbiór <math>\mathbb{R}^2</math> nie jest zwarty. | ||
Wersja z 12:37, 31 sie 2023
Ciągi w przestrzeniach metrycznych
Ćwiczenie 2.1.
Niech będzie przestrzenią metryczną, niech będzie ciągiem oraz niech Udowodnić, że jeśli oraz jest dowolnym podciągiem ciągu to
Ćwiczenie 2.2.
Niech będzie przestrzenią metryczną, ciągiem oraz niech Udowodnić, że jeśli jest ciągiem zbieżnym oraz jest jego dowolnym podciągiem takim, że to także
Ćwiczenie 2.3.
Niech będą przestrzeniami metrycznymi dla ciągiem w
(w
szczególności
dla
oraz ).
Udowodnić, że:
(1)
,
wtedy i tylko wtedy, gdy
dla
(2) Ciąg
spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy
ciągi spełniają warunek Cauchy'ego dla
Ćwiczenie 2.4.
Pokazać z definicji, że (z metryką euklidesową) nie jest zbiorem zwartym.
Ćwiczenie 2.5.
Jakie zbiory są zwarte w przestrzeni metrycznej dyskretnej? Odpowiedź uzasadnij.
Ćwiczenie 2.6.
Niech będzie przestrzenią metryczną
oraz Które z implikacji są prawdziwe:
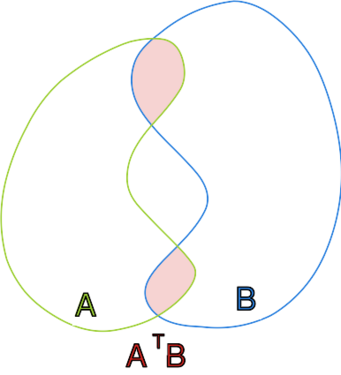
"jeśli zbiory i są spójne, to zbiór jest
spójny";
"jeśli zbiory i są spójne, to zbiór jest
spójny";
"jeśli zbiór jest spójny, to zbiory i są
spójne".
Ćwiczenie 2.7.
Niech będzie przestrzenią metryczną
oraz Które z implikacji są prawdziwe:
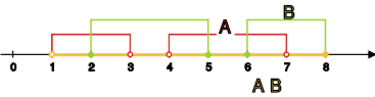
"jeśli zbiory i są zwarte, to zbiór jest
zwarty";
"jeśli zbiór jest zwarty, to zbiory i są
zwarte".
Ćwiczenie 2.8.
Opisać jak wyglądają ciągi Cauchy'ego w przestrzeni metrycznej dyskretnej.
Ćwiczenie 2.9.
Rozważmy płaszczyznę z metryką kolejową z węzłem Zbadać zbieżność dwóch ciągów: i w tej metryce, gdy oraz dla