Analiza matematyczna 2/Ćwiczenia 2: Ciągi w przestrzeniach metrycznych: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „.</math>” na „</math>.” |
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
||
| (Nie pokazano 2 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 8: | Linia 8: | ||
jeśli <math>\lim\limits_{n\rightarrow +\infty} x_n=g</math> oraz | jeśli <math>\lim\limits_{n\rightarrow +\infty} x_n=g</math> oraz | ||
<math>\big\{x_{n_k}\big\}</math> jest dowolnym podciągiem ciągu | <math>\big\{x_{n_k}\big\}</math> jest dowolnym podciągiem ciągu | ||
<math>\{x_n\} | <math>\{x_n\}</math>, to | ||
<center><math>\lim\limits_{k\rightarrow +\infty} x_{n_k} | <center><math>\lim\limits_{k\rightarrow +\infty} x_{n_k} | ||
| Linia 61: | Linia 61: | ||
Z jedyności granicy | Z jedyności granicy | ||
(patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_6|twierdzenie 2.6.]]) mamy, że | (patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_6|twierdzenie 2.6.]]) mamy, że | ||
<math>g=g_1 | <math>g=g_1</math>, co należało dowieść. | ||
</div></div> | </div></div> | ||
| Linia 102: | Linia 102: | ||
<center><math>\exists N\in\mathbb{N}\ \forall n\ge N: | <center><math>\exists N\in\mathbb{N}\ \forall n\ge N: | ||
d(a_n,a)<\varepsilon | d(a_n,a)<\varepsilon</math>,</center> | ||
</math></center> | |||
gdzie | gdzie | ||
| Linia 120: | Linia 119: | ||
d(a_n,a) | d(a_n,a) | ||
< | < | ||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
| Linia 152: | Linia 150: | ||
\sqrt{k\cdot \frac{\varepsilon^2}{k}} | \sqrt{k\cdot \frac{\varepsilon^2}{k}} | ||
= | = | ||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
| Linia 159: | Linia 156: | ||
<center><math>\forall\varepsilon>0 | <center><math>\forall\varepsilon>0 | ||
\exists N\in\mathbb{N}\ \forall n\ge N: | \exists N\in\mathbb{N}\ \forall n\ge N: | ||
d(a_n,a)<\varepsilon | d(a_n,a)<\varepsilon</math>,</center> | ||
</math></center> | |||
co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n= a</math><br> | co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n= a</math><br> | ||
| Linia 192: | Linia 188: | ||
d(a_n,a_m) | d(a_n,a_m) | ||
< | < | ||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
| Linia 227: | Linia 222: | ||
\sqrt{k\cdot \frac{\varepsilon^2}{k}} | \sqrt{k\cdot \frac{\varepsilon^2}{k}} | ||
= | = | ||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
| Linia 340: | Linia 334: | ||
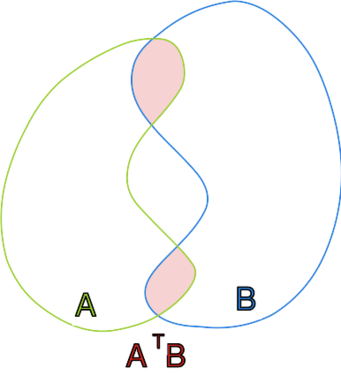
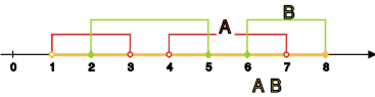
Przecięcie zbiorów spójnych nie musi być zbiorem | Przecięcie zbiorów spójnych nie musi być zbiorem | ||
spójnym. | spójnym. | ||
Rysunek przedstawia dwa zbiory spójne <math>A,B\subseteq \mathbb{R}^2 | Rysunek przedstawia dwa zbiory spójne <math>A,B\subseteq \mathbb{R}^2</math>, | ||
których przecięcie <math>A\cap B</math> nie jest spójne.<br> | których przecięcie <math>A\cap B</math> nie jest spójne.<br> | ||
Suma zbiorów spójnych nie musi być zbiorem | Suma zbiorów spójnych nie musi być zbiorem | ||
| Linia 421: | Linia 415: | ||
<center> | <center> | ||
<math>\exists N\in\mathbb{N}\ \forall n,m\ge N: | <math>\exists N\in\mathbb{N}\ \forall n,m\ge N: | ||
d(x_n,x_m)<\frac{1}{2} | d(x_n,x_m)<\frac{1}{2}</math> | ||
</math> | |||
</center> | </center> | ||
Ale metryka dyskretna przyjmuje tylko wartości <math>0</math> i <math>1 | Ale metryka dyskretna przyjmuje tylko wartości <math>0</math> i <math>1</math>, | ||
zatem dla dowolnych <math>n,m\ge N</math> mamy <math>d(x_n,x_m)=0 | zatem dla dowolnych <math>n,m\ge N</math> mamy <math>d(x_n,x_m)=0</math>, | ||
a to z kolei oznacza, że <math>x_n=x_m</math>. | a to z kolei oznacza, że <math>x_n=x_m</math>. | ||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
| Linia 432: | Linia 425: | ||
<center> | <center> | ||
<math>\forall n\ge N: | <math>\forall n\ge N: | ||
x_n=x_N | x_n=x_N</math>, | ||
</math> | |||
</center> | </center> | ||
| Linia 489: | Linia 481: | ||
\sqrt{0^2+\bigg(1+\frac{1}{n}-1\bigg)} | \sqrt{0^2+\bigg(1+\frac{1}{n}-1\bigg)} | ||
= | = | ||
\frac{1}{n} | \frac{1}{n}</math>,</center> | ||
</math></center> | |||
zatem <math>d(y_n,y_0)\longrightarrow 0</math>, gdy <math>n\rightarrow +\infty | zatem <math>d(y_n,y_0)\longrightarrow 0</math>, gdy <math>n\rightarrow +\infty</math>, | ||
a to oznacza, że <math>y_n\xrightarrow[d]{} y_0=(1,0)</math>. | a to oznacza, że <math>y_n\xrightarrow[d]{} y_0=(1,0)</math>. | ||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 21:46, 11 wrz 2023
Ciągi w przestrzeniach metrycznych
Ćwiczenie 2.1.
Niech będzie przestrzenią metryczną, niech będzie ciągiem oraz niech . Udowodnić, że jeśli oraz jest dowolnym podciągiem ciągu , to
Ćwiczenie 2.2.
Niech będzie przestrzenią metryczną, ciągiem oraz niech Udowodnić, że jeśli jest ciągiem zbieżnym oraz jest jego dowolnym podciągiem takim, że to także
Ćwiczenie 2.3.
Niech będą przestrzeniami metrycznymi dla ciągiem w
(w
szczególności
dla
oraz ).
Udowodnić, że:
(1)
,
wtedy i tylko wtedy, gdy
dla .
(2) Ciąg
spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy
ciągi spełniają warunek Cauchy'ego dla
Ćwiczenie 2.4.
Pokazać z definicji, że (z metryką euklidesową) nie jest zbiorem zwartym.
Ćwiczenie 2.5.
Jakie zbiory są zwarte w przestrzeni metrycznej dyskretnej? Odpowiedź uzasadnij.
Ćwiczenie 2.6.
Niech będzie przestrzenią metryczną
oraz . Które z implikacji są prawdziwe:
"jeśli zbiory i są spójne, to zbiór jest
spójny";
"jeśli zbiory i są spójne, to zbiór jest
spójny";
"jeśli zbiór jest spójny, to zbiory i są
spójne".
Ćwiczenie 2.7.
Niech będzie przestrzenią metryczną
oraz . Które z implikacji są prawdziwe:
"jeśli zbiory i są zwarte, to zbiór jest
zwarty";
"jeśli zbiór jest zwarty, to zbiory i są
zwarte".
Ćwiczenie 2.8.
Opisać jak wyglądają ciągi Cauchy'ego w przestrzeni metrycznej dyskretnej.
Ćwiczenie 2.9.
Rozważmy płaszczyznę z metryką kolejową z węzłem . Zbadać zbieżność dwóch ciągów: i w tej metryce, gdy oraz dla .