MN14

Całkowanie

<<< Powrót do strony głównej przedmiotu Metody numeryczne

Zajmiemy się teraz zadaniem całkowania numerycznego. Polega ono na obliczeniu (a raczej przybliżeniu) całki oznaczonej

$S(f)=\underset{a}{\overset{b}{\int }}f(x)dx,$

gdzie $-\mathrm{\infty }<a<b<+\mathrm{\infty }$, a $f$ należy do pewnej klasy $F$ funkcji rzeczywistych określonych i całkowalnych w sensie Riemanna na całym przedziale $[a,b]$.

Każdy, kto przeszedł przez kurs całkowania wie, że obliczanie całek rozumiane jako znalezienie elementarnego wzoru na funkcję pierwotną może być trudne, bardzo trudne, a nawet niewykonalne. Tymczasem zadanie przybliżonego wyznaczenia wartości całki daje się w dużej mierze zautomatyzować z całkiem dobrym skutkiem.

Obliczanie całek jest wymagane w bardzo wielu zadaniach inżynierskich i naukowych. Całki z funkcji (bardzo) wielu zmiennych (które na swój sposób są szczególnie trudne do obliczenia) znajdują ważne zastosowania w bankowości i finansach.

Będziemy zakładać, że mamy możliwość obliczania wartości funkcji $f$, a w niektórych przypadkach również jej pochodnych, o ile istnieją. Dokładna całka $S(f)$ będzie więc w ogólności przybliżana wartością $A(f)$, która zależy tylko od wartości $f$ i ewentualnie jej pochodnych w skończonej liczbie punktów.

Kwadratury

Kwadraturami nazywamy funkcjonały liniowe $Q:F\to R$ postaci

$Q(f)=\sum _{i=0}^n{a}_{i}f(x_i)$,

albo ogólniej

$Q(f)=\sum _{i=0}^k\sum _{j=0}^{n_i-1}{a}_{i,j}{f}^{(j)}(x_i),$

gdzie $x_i$ są punktami z $[a,b]$, a $a_i$ (albo $a_{i,j}$) są pewnymi współczynnikami rzeczywistymi. Zauważmy, że obliczenia kwadratur są dopuszczalne w naszym modelu obliczeniowym, mogą więc służyć jako sposób przybliżania całki.

Jeden z możliwych sposobów konstrukcji kwadratur jest następujący. Najpierw wybieramy węzły $x_j$ (pojedyncze lub wielokrotne), budujemy wielomian interpolacyjny odpowiadający tym węzłom, a następnie całkujemy go. Ponieważ postać wielomianu interpolacyjnego zależy tylko od danej informacji o $f$, otrzymana w ten sposób wartość też będzie zależeć tylko od tej informacji, a w konsekwencji funkcjonał wynikowy będzie takiej postaci, jak wyżej. Są to tzw. kwadratury interpolacyjne.

Definicja

Kwadraturę $Q^I$ opartą na węzłach o łącznej krotności $n+1$ nazywamy interpolacyjną, jeśli

$Q^I(f)=\underset{a}{\overset{b}{\int }}{w}_f(x)dx,$

gdzie $w_f$ jest wielomianem interpolacyjnym funkcji $f$ stopnia co najwyżej $n$, opartym na tych węzłach.

Współczynniki kwadratur interpolacyjnych można łatwo wyliczyć. Rozpatrzmy dla uproszczenia przypadek, gdy węzły są jednokrotne. Zapisując wielomian interpolacyjny w postaci jego rozwinięcia w bazie kanonicznej Lagrange'a $l_i$, otrzymujemy

$Q^I(f)=\underset{a}{\overset{b}{\int }}\sum _{i=0}^{n}f(x_i)l_i(x)dx=\sum _{i=0}^{n}f(x_i)\underset{a}{\overset{b}{\int }}{l}_i(x)dx,$

a stąd i z postaci $l_i$,

$a_i=\underset{a}{\overset{b}{\int }}\frac{(x-x_0)\cdots (x-x_{i-1})(x-x_{i+1})\cdots (x-x_n)}{(x_i-x_0)\cdots (x_i-x_{i-1})(x_i-x_{i+1})\cdots (x_i-x_n)}dx$,

$0\le i\le n$.

Podamy teraz kilka przykładów.

Kwadratura prostokątów jest oparta na jednym węźle $x_0=(a+b)/2$,

$Q_0^I(f)=(b-a)f\left(\frac{a+b}{2}\right)$

Kwadratura prostokątów

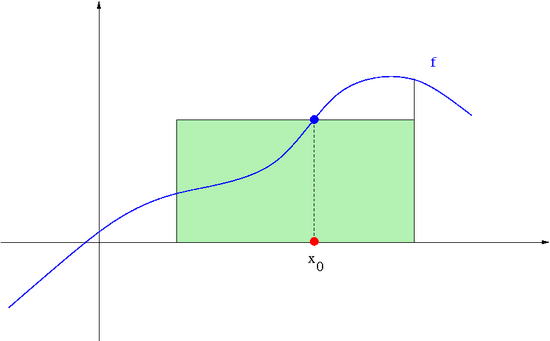
Kwadratura trapezów jest oparta na jednokrotnych węzłach $x_0=a$, $x_1=b$ i jest równa polu odpowiedniego trapezu,

$Q_1^I(f)=T(f)=\frac{b-a}{2}(f(a)+f(b))$

Kwadratura trapezów

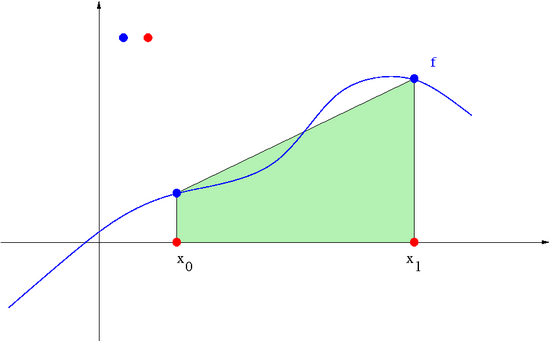
Kwadratura parabol (Simpsona) jest oparta na jednokrotnych węzłach $x_0=a$, $x_1=b$, $x_2=(a+b)/2$, i jest równa polu pod parabolą interpolującą $f$ w tych węzłach,

$Q_2^I(f)=P(f)=\frac{b-a}{6}(f(a)+4f(\frac{a+b}{2})+f(b))$

Zauważmy, że kwadratury trapezów i parabol są oparte na węzłach jednokrotnych i równoodległych, przy czym $x_0=a$ i $x_n=b$. Ogólnie, kwadratury interpolacyjne oparte na węzłach równoodległych $x_i=a+(b-a)i/n$, $0\le i\le n$, nazywamy kwadraturami Newtona--Cotesa.

Błąd kwadratur interpolacyjnych

Zajmiemy się teraz błędem kwadratur interpolacyjnych. Przypomnijmy, że $F_M^r([a,b])$ oznacza klasę funkcji $(r+1)$ razy różniczkowalnych w sposób ciągły i takich, że $|f^{(r+1)}(x)|\le M$, $\mathrm{\forall }x$.

Twierdzenie O błędzie kwadratur interpolacyjnych

Niech $Q^I$ będzie kwadraturą interpolacyjną opartą na (jednokrotnych lub wielokrotnych) węzłach $x_i$, $0\le i\le n$. Jeśli $f\in F_M^n([a,b])$, to

$|S(f)-Q^I(f)|\le \frac{M}{(n+1)!}(b-a{)}^{n+2}.$

W klasie $F_M^n([a,b])$ maksymalny błąd kwadratury $Q^I$ wynosi

$\underset{f\in F_M^n([a,b])}{\sup }|S(f)-Q^I(f)|=\frac{M}{(n+1)!}\underset{a}{\overset{b}{\int }}|(x-x_0)(x-x_1)\cdots (x-x_n)|dx$

Dowód

Korzystając ze znanego nam już wzoru na błąd interpolacji wielomianowej, mamy

$S(f)-Q^I(f)=\underset{a}{\overset{b}{\int }}(x-x_0)(x-x_1)\cdots (x-x_n)f(x_0,x_1,\dots ,x_n,x)dx$

Stąd, jeśli $f\in F_M^n([a,b])$, to

$|S(f)-Q^I(f)|\le \underset{a}{\overset{b}{\int }}(b-a{)}^{n+1}\frac{M}{(n+1)!}dx=(b-a{)}^{n+2}\frac{M}{(n+1)!}$

Ograniczenie górne w dokładnej formule na błąd w klasie $F_M^n([a,b])$ wynika bezpośrednio. Aby pokazać ograniczenie dolne zauważmy, że dla funkcji $g$ takiej, że $g^{(n+1)}$ przyjmuje na przedziałach $(a,x_0)$, $(x_0,x_1)$, $\dots$, $(x_n,b)$ naprzemiennie wartości $M$ i $-M$ mamy

$|S(g)-Q^I(g)|=\frac{M}{(n+1)!}\underset{a}{\overset{b}{\int }}|(x-x_0)(x-x_1)\cdots (x-x_n)|dx$

Co prawda, $g$ nie jest w $F_M^n([a,b])$, ale może być dla dowolnego $ϵ>0$ przybliżana funkcjami $f_{ϵ}\in F_M^n([a,b])$ w ten sposób, że całka

$\underset{a}{\overset{b}{\int }}|(x-x_0)\cdots (x-x_n)(f-g{)}^{(n+1)}(x)|dx\le ϵ(n+1)!$

Zapisując $f_{ϵ}=g+(f_{ϵ}-g)$ mamy

$\begin{array}{rlr}|S(f_{ϵ})-Q^I(f_{ϵ})|& \le & |S(g)-Q^I(g)|+|S(f_{ϵ}-g)-Q^I(f_{ϵ}-g)|\\ & \le & \frac{M}{(n+1)!}\underset{a}{\overset{b}{\int }}|(x-x_0)\cdots (x-x_n)|dx+ϵ,\end{array}$

co wobec dowolności $ϵ$ daje dowód twierdzenia.

W szczególnych przypadkach kwadratur trapezów $T$ i parabol $P$ możemy otrzymać innego rodzaju formuły na błąd.

Twierdzenie O postaci błędu kwadratury trapezów i Simpsona

Jeśli $f\in C^{(2)}([a,b])$, to dla kwadratury trapezów mamy

$S(f)-T(f)=-\frac{(b-a{)}^3}{12}{f}^{(2)}({\xi }_1)$

Jeśli $f\in C^{(4)}([a,b])$, to dla kwadratury parabol mamy

$S(f)-P(f)=-\frac{(b-a{)}^5}{2280}{f}^{(4)}({\xi }_2)$

(${\xi }_1,{\xi }_2\in [a,b]$).

Dowód

Najpierw udowodnimy część dotyczącą kwadratury trapezów. Ze wzoru na błąd kwadratury,

$S(f)-T(f)=\underset{a}{\overset{b}{\int }}(x-a)(x-b)f(a,b,x)dx$

Ponieważ funkcja $x\mapsto f(a,b,x)$ jest ciągła, a wielomian $(x-a)(x-b)$ przyjmuje jedynie wartości nieujemne, można zastosować twierdzenie o wartości średniej dla całki, aby otrzymać

$\begin{array}{rl}S(f)-T(f)& =f(a,b,c)\underset{a}{\overset{b}{\int }}(x-a)(x-b)dx\\ & =-\frac{f^{(2)}({\xi }_1)}{2!}\frac{(b-a{)}^3}{6},\end{array}$

dla pewnych $c,{\xi }_1\in [a,b]$.

Teraz zajmiemy się kwadraturą parabol. Niech $w_{f,2}\in {\mathrm{\Pi }}_2$ i $w_{f,3}\in {\mathrm{\Pi }}_3$ będą wielomianami interpolacyjnymi funkcji $f$ odpowiednio dla węzłów $a,b,(a+b)//2$ oraz $a,b,(a+b)//2,(a+b)//2$. Wtedy

$w_{f,3}(x)=w_{f,2}(x)+f(a,b,\frac{a+b}{2},\frac{a+b}{2})(x-a)(x-\frac{a+b}{2})(x-b).$

Wobec

$\underset{a}{\overset{b}{\int }}(x-a)\left(\frac{a+b}{2}\right)(x-b)dx=0$

mamy

$P(f)=\underset{a}{\overset{b}{\int }}{w}_{f,2}(x)dx=\underset{a}{\overset{b}{\int }}{w}_{f,3}(x)dx$

Stąd i ze wzoru na błąd interpolacji Hermite'a otrzymujemy

$\begin{array}{r}S(f)-P(f)=\underset{a}{\overset{b}{\int }}(f-w_{f,3})(x)dx\\ & & =\underset{a}{\overset{b}{\int }}(x-a)(x-\frac{a+b}{2}{)}^2(x-b)f(a,b,\frac{a+b}{2},\frac{a+b}{2},x)dx.\end{array}$

Ponieważ wielomian $(x-a)(x-(a+b)/2{)}^2(x-b)$ jest niedodatni na $[a,b]$, możemy znów zastosować twierdzenie o wartości średniej. Mamy

$\begin{array}{rl}S(f)-P(f)& =f(a,b,\frac{a+b}{2},\frac{a+b}{2},c)\\ & & \underset{a}{\overset{b}{\int }}(x-a)(x-\frac{a+b}{2}{)}^2(x-b)dx\\ & =-\frac{f^{(4)}({\xi }_2)}{4!}\frac{(b-a{)}^5}{120},\end{array}$

co kończy dowód.

Kwadratury złożone

Chcielibyśmy, aby błąd kwadratur malał do zera, gdy liczba węzłów rośnie do nieskończoności. Można to osiągnąć stosując np. kwadratury złożone. Są to kwadratury, które powstają przez scałkowanie funkcji kawałkami wielomianowej interpolującej $f$.

Georg Riemann
Zobacz biografię

Prostym przykładem kwadratury złożonej jest suma Riemanna,

$\overline{Q}(f)=\sum _{i=0}^n(t_{i+1}-t_i)f(x_i),$

gdzie $a=t_0<t_1<\cdots <t_{n+1}=b$ oraz $x_i\in [t_i,t_{i+1}]$. Jeśli średnica podziału, $\underset{0\le i\le n}{\max }(t_i-t_{i-1})$, maleje do zera, to $\underset{n\to \mathrm{\infty }}{\lim }\overline{Q}(f)=S(f)$.

Będziemy rozpatrywać kwadratury złożone postaci

$\overline{Q}(f)=\underset{a}{\overset{b}{\int }}{\overline{w}}_f(x)dx,$

gdzie ${\overline{w}}_f$ jest kawałkami wielomianem. Dokładniej, dla danego $n$ kładziemy $t_i=a+(b-a)i/k$, $0\le i\le k$, a następnie dla każdego $i$ wybieramy dowolne węzły $x_{i,j}\in [t_{i-1},t_i]$, $0\le j\le r$. Wtedy ${\overline{w}}_f$ jest na każdym przedziale wielomianem interpolacyjnym funkcji $f$ stopnia co najwyżej $r$ opartym na węzłach $x_{i,j}$. Kwadratura $\overline{Q}$ korzysta z węzłów o łącznej krotności $n\le k(r+1)$.

Twierdzenie O błędzie kwadratur złożonych

Błąd kwadratury złożonej $\overline{Q}(f)$ w klasie $F_M^r([a,b])$ jest ograniczony przez

$\underset{f\in F_M^r([a,b])}{\sup }|S(f)-\overline{Q}(f)|\le \frac{(b-a{)}^{r+2}}{k^{r+1}}\frac{M}{(r+1)!}\le C(\frac{1}{n}{)}^{r+1},$

gdzie

$C=\frac{M(r+1{)}^{r+1}(b-a{)}^{r+2}}{(r+1)!}$

Dowód

Twierdzenie to jest bezpośrednim wnioskiem z twierdzenia o błędzie kwadratur interpolacyjnych. Mamy bowiem

$\begin{array}{rlr}|S(f)-\overline{Q}(f)|& \le & \sum _{i=1}^k\underset{t_{i-1}}{\overset{t_i}{\int }}|f(x)-{\overline{w}}_f(x)|dx\\ & \le & \sum _{i=1}^k(\frac{b-a}{k}{)}^{r+2}\frac{M}{(r+1)!}=\frac{(b-a{)}^{r+2}}{k^{r+1}}\frac{M}{(r+1)!},\end{array}$

co kończy dowód.

W klasie $F_M^r([a,b])$, błąd kwadratur złożonych jest rzędu $n^{-(r+1)}$. Można pokazać, że błąd każdej innej metody całkowania korzystającej jedynie z wartości funkcji w $n$ punktach nie może w klasie $F_M^r([a,b])$ maleć szybciej niż $n^{-(r+1)}$. Podane kwadratury złożone mają więc optymalny rząd zbieżności.

Zajmiemy się teraz błędem szczególnych kwadratur złożonych, mianowicie złożonych kwadratur trapezów ${\overline{T}}_k$ i parabol ${\overline{P}}_k$. Powstają one przez zastosowanie na każdym przedziale $[t_{i-1},t_i]$ odpowiednio kwadratur trapezów $T$ i parabol $P$.

Złożona kwadratura trapezów

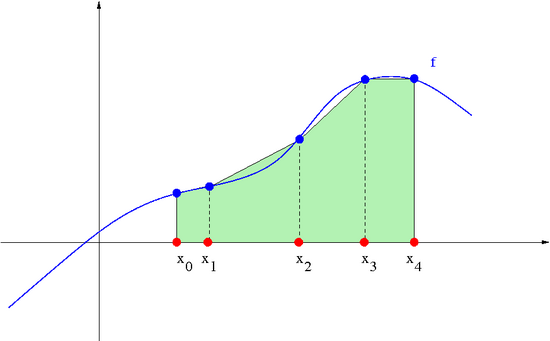
Jak łatwo się przekonać,

${\overline{T}}_k(f)=\frac{b-a}{k}(\frac{f(a)+f(b)}{2}+\sum _{j=1}^{k-1}f(\frac{j}{k}\left)\right),$

oraz

${\overline{P}}_k(f)=\frac{b-a}{3k}(\frac{f(a)+f(b)}{2}+\sum _{j=1}^{k-1}f(\frac{j}{k})+2\sum _{j=1}^{k}f(\frac{2j-1}{2k}\left)\right).$

Twierdzenie O postaci błędu złożonych kwadratur trapezów i Simpsona

Jeśli $f\in C^{(2)}([a,b])$, to

$S(f)-{\overline{T}}_k(f)=-\frac{(b-a{)}^3}{12k^2}{f}^{(2)}({\xi }_1)$

Jeśli $f\in C^{(4)}([a,b])$, to

$S(f)-{\overline{P}}_k(f)=-\frac{(b-a{)}^5}{2280k^4}{f}^{(4)}({\xi }_2)$

Dowód

Dla kwadratury trapezów mamy

$\begin{array}{r}S(f)-{\overline{T}}_k(f)=-\sum _{i=1}^k\frac{(b-a{)}^3}{12k^3}{f}^{(2)}({\alpha }_i)\\ & & =-\frac{(b-a{)}^3}{12k^2}\frac{1}{k}\sum _{i=1}^k{f}^{(2)}({\alpha }_i)=-\frac{(b-a{)}^3}{12k^2}{f}^{(2)}({\xi }_1),\end{array}$

a dla kwadratury parabol podobnie

$\begin{array}{r}S(f)-{\overline{P}}_k(f)=-\sum _{i=1}^k\frac{(b-a{)}^5}{2280k^5}{f}^{(4)}({\beta }_i)\\ & & =-\frac{(b-a{)}^5}{2280k^4}\frac{1}{k}\sum _{i=1}^k{f}^{(4)}({\beta }_i)=-\frac{(b-a{)}^5}{2280k^4}{f}^{(4)}({\xi }_2).\end{array}$

Kwadratura parabol ma więc optymalny rząd zbieżności nie tylko w klasie $F_M^2([a,b])$, ale też w $F_M^3([a,b])$.

Przyspieszanie zbieżności kwadratur

W praktyce często stosuje się obliczanie kwadratur poprzez zagęszczanie podziału przedziału $[a,b]$. Na przykład, dla złożonej kwadratury trapezów zachodzi następujący wygodny wzór rekurencyjny:

${\overline{T}}_{2k}=\frac{1}{2}({\overline{T}}_k(f)+\frac{b-a}{k}\sum _{i=1}^{k}f(\frac{2i-1}{2k}\left)\right)$

Pozwala on obliczyć ${\overline{T}}_{2k}(f)$ na podstawie ${\overline{T}}_k(f)$ poprzez "doliczenie" wartości funkcji w punktach "gęstszej" siatki. W ten sposób możemy obserwować zachowanie się kolejnych przybliżeń ${\overline{T}}_{2^s}(f)$ ($s\ge 0$) całki $S(f)$. Jest to szczególnie istotne wtedy, gdy nie mamy żadnej informacji a priori o $\Vert f^{″}{\Vert }_{C([a,b])}$, a przez to nie potrafimy oszacować liczby $n$ węzłów, dla której osiągniemy pożądaną dokładność.

Jeśli funkcja jest więcej niż dwa razy różniczkowalna, to użycie złożonych kwadratur trapezów zdaje się tracić sens. Wtedy istnieją przecież kwadratury, których błąd maleje do zera szybciej niż $n^{-2}$. Okazuje się jednak, że kwadratury ${\overline{T}}_k$ mogą być podstawą dla prostej rekurencyjnej konstrukcji innych kwadratur posiadających już optymalną zbieżność. Konstrukcja ta bazuje na następującym ważnym lemacie.

Leonhard Euler
Zobacz biografię

Colin Maclaurin
Zobacz biografię

Lemat Formuła Eulera-Maclaurina

Dla funkcji $f\in C^{(2m+2)}([a,b])$, błąd złożonej kwadratury trapezów ${\overline{T}}_k$ wyraża się wzorem

$\begin{array}{rl}S(f)-{\overline{T}}_k(f)& =\sum _{i=1}^m{c}_i{h}^{2i}(f^{(2i-1)}(b)-f^{(2i-1)}(a))\\ & & +c_{m+1}{h}^{2m+2}(b-a)f^{(2m+2)}({\xi }_{m,k}),\end{array}$

gdzie $h=(b-a)/k$, ${\xi }_{m,k}\in [a,b]$, a $c_i$ są pewnymi stałymi liczbowymi. Mamy $c_1=-1/12$, $c_2=-1/720$ i, ogólnie, $c_i=B_i/(2i)!$, gdzie $B_i$ są tzw. liczbami Bernoulliego.

Dowód tego lematu pominiemy.

Formułę Eulera-Maclaurina można przepisać w postaci

$S(f)-{\overline{T}}_k(f)=\sum _{i=1}^m{c}_i^{(0)}(f)k^{-2i}+c_{m+1,k}^{(0)}(f)k^{-(2m+2)}$,

gdzie $c_i^{(0)}(f)=c_i(b-a{)}^{2i}(f^{(2i-1)}(b)-f^{(2i-1)}(a))$, $1\le i\le m$, oraz $c_{m+1,k}^{(0)}(f)=c_{m+1}(b-a{)}^{2m+2}{f}^{(2m+2)}({\xi }_{m+1,k})$. Zauważmy przy tym, że jeśli $f\in F_M^{2m+1}([a,b])$, to współczynniki $c_{m+1,k}^{(0)}(f)$ są wspólnie ograniczone przez $c_{m+1}(b-a{)}^{2m+2}M$.

Definiując teraz kwadraturę

${\overline{T}}_k^1(f)=\frac{4{\overline{T}}_{2k}(f)-{\overline{T}}_k(f)}{3}$,

dla $f\in C^{(4)}([a,b])$ mamy

$\begin{array}{rl}S(f)-{\overline{T}}_k^1(f)& =\frac{4(S(f)-{\overline{T}}_{2k}(f)-(S(f)-{\overline{T}}_k(f))}{3}\\ & =\frac{4}{3}(\frac{c_1^{(0)}(f)}{4k^2}+\frac{c_{2,2k}^{(0)}(f)}{4^2{k}^4})-\frac{1}{3}(\frac{c_1^{(0)}(f)}{k^2}+\frac{c_{2,k}^{(0)}(f)}{k^4})\\ & =\frac{c_{2,k}^{(1)}(f)}{k^4},\end{array}$

gdzie $c_{2,k}^{(1)}(f)=(1/12)c_{2,2k}^{(0)}(f)-(1/3)c_{2,k}^{(0)}(f)$ i jest wspólnie ograniczone dla $f\in F_M^3([a,b])$. Kwadratura $T_k^1$ ma więc optymalny w $F_M^3([a,b])$ rząd zbieżności $k^{-4}$. Proces ten można kontynuować dalej tworząc kolejne kwadratury o coraz to wyższym rzędzie zbieżności. Dokładniej, połóżmy ${\overline{T}}_k^0(f)={\overline{T}}_k(f)$ oraz, dla $s\ge 1$,

${\overline{T}}_k^s(f)=\frac{4^s{\overline{T}}_{2k}^{s-1}(f)-{\overline{T}}_k^{s-1}(f)}{4^s-1}$

Wtedy, dla $f\in F_M^{2m+1}([a,b])$, rząd zbieżności kwadratury ${\overline{T}}_k^m$ wynosi $k^{-(2m+2)}$. Rzeczywiście, sprawdziliśmy, że jest to prawdą dla $m=0,1$. Niech $m\ge 2$. Postępując indukcyjnie dla $s=1,2,\dots ,m$ mamy

$\begin{array}{r}S(f)-{\overline{T}}_k^s(f)=\frac{4^s(S(f)-{\overline{T}}_{2k}^{s-1}(f))-(S(f)-{\overline{T}}_k^{s-1}(f))}{4^s-1}\\ & & =(4^s(\sum _{i=s}^m{c}_i^{(s-1)}(f)(2k{)}^{-2i}+c_{m+1,2k}^{(s-1)}(f)(2k{)}^{-(2m+2)})\\ & & -(\sum _{i=s}^m{c}_i^{(s-1)}(f)k^{-2i}+c_{m+1,k}^{(s-1)}(f)k^{-(2m+2)}))\frac{1}{4^s-1}\\ & & =\sum _{i=s+1}^m{c}_i^{(s)}(f)k^{-2i}+c_{m+1,k}^{(s)}(f)k^{-(2m+2)},\end{array}$

ponieważ współczynniki przy $k^{-2s}$ redukują się. $c_i^{(s)}(f)$ są tutaj pewnymi nowymi stałymi, a $c_{m+1,k}^{(s)}(f)$ może być w klasie $F_M^{2m+1}([a,b])$ ograniczona przez stałą niezależną od $f$. Ostatecznie, dla $s=m$ mamy więc

$S(f)-{\overline{T}}_k^m(f)=c_{m+1,k}^{(m)}(f)k^{-(2m+2)}$

i w klasie $F_M^{2m+1}([a,b])$

$|S(f)-{\overline{T}}_k^m(f)|\le c_m{k}^{-(2m+2)}$

dla pewnej stałej $c_m$ niezależnej od $f$.

Zauważmy jeszcze, że ${\overline{T}}_k^m$ wykorzystuje $n=k{2}^m+1$ wartości $f$ w punktach równoodległych na $[a,b]$, co oznacza, że w terminach $n$ rząd zbieżności wynosi też $n^{-(2m+2)}$, a więc jest optymalny w klasie $F_M^{2m+1}([a,b])$.

Kwadratury ${\overline{T}}_k^s$ nazywane są kwadraturami Romberga. Dla danej funkcji $f$ można je łatwo konstruować, budując następującą tablicę trójkątną:

$\begin{array}{c}{\overline{T}}_1^0(f)\\ {\overline{T}}_2^0(f)& {\overline{T}}_1^1(f)\\ {\overline{T}}_4^0(f)& {\overline{T}}_2^1(f)& {\overline{T}}_1^2(f)\\ {\overline{T}}_8^0(f)& {\overline{T}}_4^1(f)& {\overline{T}}_2^2(f)& {\overline{T}}_1^3(f)\\ ⋮& ⋮& ⋮& ⋮& \ddots \\ {\overline{T}}_{2^s}^0(f)& {\overline{T}}_{2^{s-1}}^1(f)& {\overline{T}}_{2^{s-2}}^2(f)& {\overline{T}}_{2^{s-3}}^3(f)& \cdots & {\overline{T}}_1^s(f),\end{array}$

której kolumny tworzone są zgodnie z powyższymi wzorami.

Kwadratury adaptacyjne

jak wcześniej zauważyliśmy, błąd kwadratury prostej zależy m.in. od wielkości pochodnej $f^{(r+1)}$ funkcji podcałkowej. Odpowiednia kwadratura złożona wydaje się tego nie zauważać i zagęszcza podział przedziału całkowania jednostajnie, podczas gdy naturalnym i prostym wydaje się pomysł gęstszego podziału tam gdzie $|f^{(r+1)}(x)|$ jest "duża" i rzadszego tam, gdzie $f^{(r+1)}(x)|$ jest "mała". Nasz entuzjazm do tego pomysłu może jednak skutecznie ostudzić uwaga, że algorytm na wejściu zwykle nie dostaje żadnej informacji o $f^{(r+1)}$. Okazuje się, że mimo wszystko nie stoimy na straconej pozycji. Algorytm obliczający całkę dysponuje na każdym pewną dodatkową informacją o $f$ w postaci jej wartości w pewnych punktach; następny punkt (podział przedziału całkowania) może więc być wybrany na podstawie tych wartości.

Metody uzależniające swoje działanie od konkretnego zadania, które rozwiązują (w naszym przypadku od funkcji podcałkowej) nazywamy ogólnie metodami adaptacyjnymi.

Zauważmy, że poznana wcześniej metoda bisekcji przybliżonego znajdowania zera funkcji jest typową metodą adaptacyjną. Zobaczymy teraz, na przykładzie adaptacyjnej kwadratury Simpsona, jak można wykorzystać adaptację w problemie numerycznego całkowania.

Niech, tak jak poprzednio, ${\overline{P}}_k$ będzie złożoną kwadraturą Simpsona z równym podziałem przedziału całkowania na $k$ podprzedziałów, zastosowaną na odcinku $[a,b]$. W szczególności, ${\overline{P}}_1=P$ jest prostą kwadraturą Simpsona. Wtedy

$S(f)-{\overline{P}}_2(f)=-\frac{(b-a{)}^5}{2280\cdot 2^4}{f}^{(4)}({\xi }_2)$,

oraz

$\begin{array}{rl}{\overline{P}}_1(f)-{\overline{P}}_2(f)& =(S(f)-{\overline{P}}_2(f))-(S(f)-{\overline{P}}_1(f))\\ & =\frac{(b-a{)}^5}{2280}(f^{(4)}({\xi }_1)-\frac{1}{16}{f}^{(4)}({\xi }_2)),\end{array}$

${\xi }_1,{\xi }_2\in [a,b]$. Załóżmy teraz, że $f^{(4)}$ ma stały znak na $[a,b]$ oraz przedział ten jest na tyle mały, że $f^{(4)}$ jest "prawie stała". Wtedy $f^{(4)}({\xi }_1)-f^{(4)}({\xi }_2)/16\approx 15\cdot f^{(4)}({\xi }_2)/16$, a stąd otrzymujemy estymator błędu

$S(f)-{\overline{P}}_2(f)\approx -\frac{1}{15}\cdot ({\overline{P}}_1(f)-{\overline{P}}_2(f))$

Ta przybliżona równość jest podstawą adaptacyjnej kwadratury Simpsona, może bowiem posłużyć do oszacowania błędu na podprzedziałach.

Załóżmy teraz, że chcemy obliczyć wartość całki z dokładnością $\epsilon >0$. Obliczamy ${\overline{P}}_1(f)$, ${\overline{P}}_2(f)$ i sprawdzamy, czy $|{\overline{P}}_1(f)-{\overline{P}}_2(f)|/15\le \epsilon$. Jeśli tak, to ${\overline{P}}_2(f)$ jest ostateczną aproksymacją całki na $[a,b]$, a jeśli nie, to dzielimy przedział na dwa podprzedziały $[a,(a+b)/2]$ i $[(a+b)/2,b]$ i powtarzamy procedurę dla obu podprzedziałów z tolerancją błędu $\epsilon /2$. Cały proces można zgrabnie zapisać za pomocą funkcji rekurencyjnej.

Algorytm Adaptacyjna kwadratura Simpsona

---

adaptiveSimpson(a,b,f,e) 
{ 
	P1 = Simpson(a,b,f); 
	P2 = Simpson(a,(a+b)/2,f) + Simpson((a+b)/2,b,f);
	if ( abs(P1-P2) < 15*e) 
		return( P2 );
	else 
		return( adaptiveSimpson(a,(a+b)/2,f,e/2) + adaptiveSimpson((a+b)/2,b,f,e/2) );
}

Zauważmy, że funkcja ta zakończy działanie. Rzeczywiście, na podprzedziale długości $h$ chcemy obliczać całkę z dokładnością $\epsilon h/(b-a)$, a ponieważ różnica $|P1-P2|$ jest rzędu $h^5$, kryterium kończenia procedury będzie spełnione dla każdego $h$ dostatecznie małego. Podziały nie mogą więc następować w nieskończoność.

Trochę gorzej sprawa przedstawia się z błędem. Algorytm bazuje bowiem na jego estymatorze. Jeśli po zakończeniu algorytmu mamy podział na podprzedziały $a=x_0<x_1<\cdots <x_n=b$ oraz estymator działa poprawnie na każdym podprzedziale, to błąd można w przybliżeniu oszacować przez

$\sum _{j=1}^n\epsilon \cdot \frac{x_j-x_{j-1}}{b-a}=\epsilon$

Z drugiej strony, możemy czasem trafić wyjątkowo "złośliwą" funkcję. Np. jeśli $f(a+j(b-a)/4)=0$ dla $0\le j\le 4$, to już na początku estymator (fałszywie!) twierdzi, że błąd jest zerowy i kwadratura zwróci zero mimo, że rzeczywista wartość całki może znacznie różnić się od zera. Istnieją pewne techniki, które przynajmniej częściowo zapobiegają tego typu zjawiskom, ale nie będziemy ich tutaj omawiać.

Uwarunkowanie całkowania

Zadanie całkowania zadanej funkcji jest, podobnie jak zadanie sumy dwóch liczb (w końcu całkowanie ma wiele wspólnego z sumowaniem!), bardzo dobrze bezwględnie uwarunkowane, natomiast uwarunkowanie względne może być nawet patologicznie duże. Dokładniej,

Twierdzenie O uwarunkowaniu zadania całkowania

Niech $f$ będzie funkcją całkowalną. Wtedy

${\text{cond}}_{abs}(S,f)=1$

oraz

${\text{cond}}_{rel}(S,f)=\frac{S(|f|)}{|S(f)|}$,

gdzie błąd argumentu liczymy w normie $||f||=\underset{a}{\overset{b}{\int }}|f(x)|dx$.

Dowód

Biorąc zaburzoną funkcję $\tilde{f}$ taką, że $||\tilde{f}-f||\le ϵ$ mamy

$|S(\tilde{f})-S(f)|=|\underset{a}{\overset{b}{\int }}(\tilde{f}-f)(x)dx|\le ϵ$,

skąd wynika teza.

W szczególności zadanie całkowania będzie źle uwarunkowane względnie, gdy wartość całki jest bliska zeru, ale sama funkcja przyjmuje duże co do modułu wartości.

Biblioteki

W Octave dostępne są jedynie procedury całkujące funkcje skalarne jednej zmiennej na odcinku:

$I=\underset{a}{\overset{b}{\int }}f(x)dx$

Robi to funkcja DQAGP ze znakomitego pakietu QUADPACK. Najlepiej od razu posłużmy się przykładem.

Przykład: Prosta całka funkcji jednej zmiennej

Przypuśćmy, że chcemy obliczyć całkę $I=\underset{0}{\overset{1}{\int }}F(x)dx$, gdzie np. $F(x)=\sin (23x)+(1-x^2{)}^{-1/2}$. W tym celu najpierw implementujemy $F$ w Octave:

function y = F(x)
	y = sin(23*x)+1/sqrt(1-x^2);
endfunction

Aby teraz obliczyć całkę $I=\underset{0}{\overset{1}{\int }}F(x)dx$, wystarczy wywołać

I = quad("F", 0, 1);

W rzeczywistości, podobnie jak w przypadku funkcji fsolve, funkcja quad zwraca więcej informacji, można jej także przekazać dodatkowe parametry. I tak, jeśli chcemy ustawić poziom tolerancji błędu obliczenia całki:

$|I-quad(...)|\le max\{\text{ATOL},\text{RTOL}\cdot I\}$

z wartościami $\text{ATOL = 1e-3}$ i $\text{RTOL = 1e-6}$, to wywołamy funkcję przekazując jej te parametry następująco:

quad("F", 0, 1, [1e-3, 1e-6]);

Musimy jednak pamiętać, by pojęcia tolerancji "błędu" nie traktować zbyt dosłownie: tym, co naprawdę kontroluje quad podczas wyznaczania wartości całki, jest jedynie pewien estymator błędu, dlatego wartość tolerancji należy zawsze wybierać w sposób konserwatywny, czyli z pewnym zapasem bezpieczeństwa, np.

Jeśli chcemy wyznaczyć wartość całki z błędem bezwzględnym na

poziomie $10^{-6}$, ustawimy -- na wszelki wypadek -- ATOL = 1e-7, a nie, prostodusznie, ATOL = 1e-6... Musimy także pamiętać, że choć są bardzo mało prawdopodobne do spotkania w praktyce, to jednak istnieją wyuzdane funkcje, dla których estymator błędu może dać całkowicie fałszywe wartości,

przez co i obliczona całka może być obarczona dowolnie wielkim błędem.

QUADPACK

Właściwie jedynym klasycznym pakietem, jaki mamy do dyspozycji jest ponaddwudziestoletni QUADPACK. Jest to zestaw kilkunastu procedur fortranowskich, służących obliczaniu typowych całek jednowymiarowych:

Typ całki	Procedura QUADPACKa
$\underset{a}{\overset{b}{\int }}f(x)$	DQNG, DQAG, DQAGS, DQAGP
$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)$	DQAGI
$\underset{a}{\overset{b}{\int }}f(x)\cos (\omega x)$	DQAWO
$\underset{a}{\overset{b}{\int }}\frac{f(x)}{x-c}$	DQAWC

oraz spora liczba podstawowych kwadratur, na których oparto te ogólne. Nazwy procedur rozszyfrowuje się podobnie jak nazwy procedur LAPACKa, zatem

• przedrostek D w nazwie każdej procedury wymienionej w tabeli (np. DQAGI) oznacza, że będzie działać na liczbach typu double (całkując funkcję $f$ zwracającą wartości tego samego typu). Gdybyśmy chcieli użyć pojedynczej precyzji, użylibyśmy nazwy procedury bez przedrostka.
• Kolejna litera, Q, oczywiście oznacza kwadraturę (Quadrature).
• Trzecia litera --- A lub N --- oznacza, odpowiednio, kwadraturę adaptacyjną lub nieadaptacyjną. Jak wiadomo, w praktyce lepiej sprawdzają się kwadratury adaptacyjne, potrafiące w jakiejś mierze dostosować się do przebiegu funkcji podcałkowej. Kwadratury nieadaptacyjne nie mają tej własności. Mogą natomiast, dla pewnych funkcji podcałkowych, okazać się tańsze, warto więc je stosować, gdy wiemy a priori, że adaptacja niewiele pomoże: np. do wolnozmiennych funkcji.
• Pozostałe litery precyzują typ liczonej całki i zakres ingerencji użytkownika; G --- "zwykła" całka, bez wagi, W --- całka z wagą, O --- dla funkcji silnie oscylujących, C --- wartość główna całki (tzw. całka Cauchy'ego), I --- przedział nieskończony, S --- możliwe osobliwości, P --- użytkownik poda listę punktów, gdzie są osobliwości.

GSL

Biblioteka GSL reimplementuje podstawowe procedury QUADPACKa w języku C. Procedury GSL mają nazwy analogiczne, jak procedury QUADPACKa, ale z przedrostkiem gsl_integration, jak w poniższym przykładzie, gdzie wywołamy odpowiednik procedury DQAG: funkcję gsl_integration_qag.

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_integration.h>

double F(double X, void * param) /* wrapper dla funkcji sin(x)/x */
{
	return(sin(X)/X);
}

int main(void)
{
	gsl_function f; /* argument z funkcją podcałkową */

	double A,ABSERR,B, EPSABS,EPSREL,RESULT;
	int IER,NEVAL;

	gsl_integration_workspace *workspace;

	int KEY, LIMIT; 

	/* przygotowujemy argument z funkcją podcałkową */
	f.function = &F;
	
	A = 0.0E0; B = 10*M_PI; /* przedział całkowania */
	EPSABS = 0.0E0; EPSREL = 1.0E-3; /* tolerancja błędu */

	/* parametry specyficzne dla QAG */
	KEY = 1; /* tzn. użyj minimalnej liczby punktów kwadratury bazowej */
	LIMIT = 100; /* maksymalny podział przedziału całkowania */
	workspace  = gsl_integration_workspace_alloc(LIMIT);
	
	/* całkujemy: QAG! */

	IER = gsl_integration_qag(&f, A, B, EPSABS, EPSREL, 
					LIMIT, KEY, workspace, &RESULT, &ABSERR);

	if (IER != 0)
		fprintf(stderr,"GSL_QAG: Kłopoty z całkowaniem\n");
	fprintf(stderr,"Całka: %g Est. błąd: %g IER: %d\n", RESULT, ABSERR,  IER);

	gsl_integration_workspace_free(workspace);
	
	return(0);
}

W powyższym przykładzie specjalnie pozostawiliśmy oznaczenia wykorzystywane w poprzednim programie. Jak widać, funkcje całkujące GSL mają bardzo podobną składnię do odpowiadających im funkcji QUADPACKa.

Miłym rozszerzeniem funkcjonalności jest możliwość przekazywania parametrów do wnętrza funkcji podcałkowej.

Różniczkowanie

<<< Powrót do strony głównej przedmiotu Metody numeryczne

Z zadaniem numerycznego różniczkowania zadanej funkcji spotykamy się często w numeryce. Rzeczywiście, jeśli przypomnimy sobie metodę siecznych, była to po prostu metoda Newtona, w której pochodną przybliżono pewnym ilorazem różnicowym:

$x_{k+1}=x_k-\frac{f(x_k)}{g_k}$,

gdzie

$g_k=\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}\approx f^{\prime }(x_k)$.

Zauważmy, że nie jest to jedyny możliwy wzór na przybliżoną metodę Newtona, równie dobrze(? --- to się dopiero okaże!) moglibyśmy wziąć

$g_k=\frac{f(x_k+h)-f(x_k)}{h}$

dla dostatecznie małego $h$.

Podobne formuły są także konieczne do konstrukcji metod numerycznego rozwiązywania równań różniczkowych, gdzie w naturalny sposób pojawia się konieczność operowania pochodną nieznanej funkcji.

Metody różnicowe

Rozważmy najprostszy sposób aproksymacji pochodnej $f^{\prime }(x)$, oparty na różnicy dzielonej w przód, gdyż ze wzoru Taylora

$f(x+h)=f(x)+f^{\prime }(x)h+O(h^2)$,

pomijając człony rzędu $h^2$, dostajemy przybliżenie

$f^{\prime }(x)\approx \frac{f(x+h)-f(x)}{h}$,

a dokładniej,

$f^{\prime }(x)=\frac{f(x+h)-f(x)}{h}+O(h)$

Podobną jakość aproksymacji dostaniemy, biorąc różnicę dzieloną w tył,

$f^{\prime }(x)=\frac{f(x)-f(x-h)}{h}+O(h)$

Nietrudno przekonać się, że wzięcie średniej arytmetycznej tych dwóch aproksymacji daje tzw. różnicę centralną, która ma wyższy rząd aproksymacji, gdyż

$f^{\prime }(x)=\frac{f(x+h)-f(x-h)}{2h}+O(h^2)$,

co znaczy, że dwukrotnie zmniejszając $h$, powinniśmy się spodziewać aż czterokrotnego zmniejszenia błędu aproksymacji pochodnej!

Jeśli chcemy uzyskać jeszcze wyższy rząd aproksymacji pochodnej, często jako wyrażenie aproksymujące przyjmuje się pochodną wielomianu interpolacyjnego. Rzeczywiście, niech $w_n$ będzie wielomianem interpolującym funkcję $f$ w parami różnych węzłach $x_0<\cdots <x_n$, tzn.

$w_n(x)=\sum _{i=0}^{n}f(x_i)l_i(x)$,

gdzie $l_i(x)$ są wielomianami bazowymi Lagrange'a. Wtedy

$f^{\prime }(x)\approx {w_n}^{\prime }(x)=\sum _{i=0}^{n}f(x_i){l_i}^{\prime }(x)$,

przy czym można wykazać, że zachodzi

Twierdzenie O błędzie aproksymacji pochodnej za pomocą pochodnej wielomianu interpolacyjnego

Niech $w_n$ będzie wielomianem interpolującym funkcję $f\in C^{n+2}[a,b]$ w równoodległych węzłach $a,a+h,a+2h,\dots ,b$, gdzie $h=(b-a)/n$. Wtedy zachodzi

$f^{\prime }(x)-{w_n}^{\prime }(x)=O(h^n)\mathrm{\forall }x\in [a,b]$

Wszystkie wprowadzone powyżej metody interpolacji oparte na wielomianie Taylora w rzeczywistości dadzą się sprowadzić do pochodnej wielomianu interpolacyjnego. Rzeczywiście,

• różnica w przód to aproksymacja $f^{\prime }(x)$ pochodną wielomianu opartego na węzłach $x$ i $x+h$,
• różnica w tył to aproksymacja $f^{\prime }(x)$ pochodną wielomianu opartego na węzłach $x$ i $x-h$,
• różnica centralna to aproksymacja $f^{\prime }(x)$ pochodną wielomianu opartego na węzłach $x-h$ i $x+h$; w tym ostatnim przypadku widzimy także, że powyższe twierdzenie nie zawsze jest ostre, bo dla różnicy centralnej byliśmy w stanie uzyskać wyższy niż minimalny gwarantowany przez twierdzenie rząd aproksymacji.

Łatwo także --- korzystając z powyższego --- wyprowadzić nowe wzory na aproksymację pochodnej, przykładowo,

$f^{\prime }(x)=\frac{1}{2h}(3f(x)-4f(x-h)+f(x-2h))+O(h^2)$

korzysta tylko z wartości $f$ na lewo od $x$ (jest to więc różniczkowanie wstecz) i też daje kwadratową aproksymację.

Analogicznie możemy aproksymować pochodne wyższych rzędów, np.

$f^{″}(x)=\frac{f(x-h)-2f(x)+f(x+h)}{h^2}+O(h^2)$

Tę formułę możemy znów uzyskać na wiele sposobów:

• wprost ze wzoru Taylora, raz dla $f(x+h)$, a raz dla $f(x-h)$,
• jako drugą pochodną wielomianu interpolacyjnego,
• jako złożenie różnicy dzielonej w przód z różnicą dzieloną w tył (co ma naśladować matematyczną zależność, że $f^{″}(x)=(f^{\prime }(x){)}^{\prime }$.

Namawiamy czytelnika do sprawdzenia, że faktycznie powyższy wzór można tak wyprowadzić.

Uwarunkowanie różniczkowania

W przeciwieństwie do całkowania, zadanie różniczkowania jest źle postawione ze względu na zaburzenie funkcji, gdy jako dopuszczalne zaburzenia przyjmiemy dowolne funkcje różniczkowalne bliskie danej funkcji w sensie normy jednostajnej. Rzeczywiście, jeśli $\tilde{f}$ jest różniczkowalna, to mimo, że $||\tilde{f}-f|{|}_{C(a,b)}\le ϵ$, wyrażenie $||{\tilde{f}}^{\prime }-f^{\prime }|{|}_{C(a,b)}$ nie jest ograniczone. Ten fakt jest źródłem praktycznych kłopotów z numerycznym przybliżaniem pochodnej, gdy np. próbujemy numerycznie różniczkować dane empiryczne: ich błąd często jest funkcją szybkozmienną.

Kłopoty numeryczne z różniczkowaniem

Rozważmy przykładowo różnicę w przód dla $h>0$. Gdyby arytmetyka której używamy miała nieskończoną precyzję, to oczywiście zachodzi

$\frac{f(x+h)-f(x)}{h}-f^{\prime }(x)=O(h)$,

i przybliżenie byłoby tym lepsze, im mniejsze byłoby $h$. Jednak w praktyce tak nie będzie, ze względu na fakt, że działamy w arytmetyce skończonej precyzji:

• dla małych $h$, mamy $f(x+h)-f(x)\approx 0$, a więc zachodzi duże ryzyko utraty cyfr przy odejmowaniu
• dla małych $h$, może zdarzyć się, że numerycznie $f{l}_{\nu }(x+h)=f{l}_{\nu }(x)$ i w konsekwencji $f{l}_{\nu }(\frac{f(x+h)-f(x)}{h})=0$.

Można więc postawić sobie pytanie, jak dobrać $h$ na tyle małe, by mieć możliwie dobrą aproksymację $f^{\prime }(x)$, a jeszcze nie odczuć zgubnych skutków wpływu arytmetyki zmiennoprzecinkowej. Formalnie, możemy pytanie postawić w sposób następujący:

Przypuśćmy, że zamiast

$f(x)$

wyznaczane jest

$\tilde{f}(x)=f(x)+{ϵ}_x$

, przy czym

$|{ϵ}_x|\le ϵ$

. Jak dobrać do

$ϵ$

parametr

$h$

w taki sposób, by aproksymacja

$\frac{\tilde{f}(x+h)-\tilde{f}(x)}{h}\approx f^{\prime }(x)$

była jak najlepsza? Mamy:

$\begin{array}{rl}|\frac{\tilde{f}(x+h)-\tilde{f}(x)}{h}-f^{\prime }(x)|& =|\frac{1}{h}((f(x+h)+{ϵ}_{x+h})-(f(x)+{ϵ}_x))-f^{\prime }(x)|\\ & \le |\frac{f(x+h)-f(x)}{h}-f^{\prime }(x)|+\frac{2ϵ}{h}\end{array}$

Ponieważ pierwszy człon wyrażenia daje się oszacować (dla dostatecznie regularnej funkcji $f$) przez $C\cdot h$, to ostatecznie dostajemy

$|\frac{\tilde{f}(x+h)-\tilde{f}(x)}{h}-f^{\prime }(x)|\le C_1(h+\frac{1}{h})$

Wyrażenie po prawej stronie jest minimalizowane dla $h=\sqrt{ϵ}$ i stąd inżynierska reguła:

Jeśli chcesz używać różnicy w przód, powinieneś wziąć $h$ równe co najmniej $\sqrt{{ϵ}_{\text{mach}}}$.

Literatura

W celu dogłębnego zapoznania się z omawianym na wykładzie materiałem, przeczytaj rozdział 7.1 -- 7.6 w

• D. Kincaid, W. Cheney Analiza numeryczna, Wydawnictwa Naukowo-Techniczne, Warszawa 2006, ISBN 83-204-3078-X.