MN09
Interpolacja wielomianowa
<<< Powrót do strony głównej przedmiotu Metody numeryczne
Zadanie interpolacji, czyli poprowadzenia krzywej zadanego rodzaju przez zestaw danych punktów, jest jednym z podstawowych zadań obliczeniowych. Stosuje się je nagminnie w najróżniejszych dziedzinach życia, np. wtedy, gdy trzeba
- na podstawie próbki sygnału dźwiękowego (to znaczy: ciągu wartości amplitud sygnału zmierzonych w kolejnych odstępach czasu), odtworzyć jego przebieg;
- przybliżyć wykres skomplikowanej (lub wręcz nieznanej) funkcji na podstawie jej wartości uprzednio stablicowanych w wybranych punktach;
Interpolację stosuje się szczególnie chętnie w samej numeryce. Na przykład idea metody siecznych polega na tym, by funkcję, której miejsca zerowego szukamy, przybliżyć prostą interpolującą tę funkcję w dwóch punktach. Metody numerycznego całkowania oraz rozwiązywania równań różniczkowych także korzystają z interpolacji.

Niech i niech będzie pewnym zbiorem funkcji . Niech będzie ustalonym zbiorem parami różnych punktów z , zwanych później węzłami.
Powiemy, że wielomian interpoluje funkcję w węzłach , gdy
Oznaczmy przez przestrzeń liniową wielomianów stopnia co najwyżej o współczynnikach rzeczywistych,
Zadanie znalezienia wielomianu interpolującego zadane wartości nazywamy zadaniem interpolacji Lagrange'a.
Twierdzenie o istnieniu i jednoznaczności zadania interpolacji Lagrange'a
Dla dowolnej funkcji istnieje dokładnie jeden wielomian interpolujący w węzłach , .
Dowód
Wybierzmy w dowolną bazę wielomianów , ,
Wtedy każdy wielomian z można jednoznacznie przedstawić w postaci rozwinięcia względem wybranej bazy. Warunkiem koniecznym i dostatecznym na to, aby wielomian interpolował jest spełnienie układu równań liniowych
z niewiadomymi , który w postaci macierzowej wygląda następująco:
Aby wykazać, że układ ten ma jednoznaczne rozwiązanie wystarczy, aby wektor zerowy był jedynym rozwiązaniem układu jednorodnego. Rzeczywiście, układ jednorodny odpowiada interpolacji danych zerowych, , . Istnienie niezerowego rozwiązania byłoby więc równoważne istnieniu niezerowego wielomianu stopnia nie większego od , który miałby różnych zer , co jest niemożliwe.
Zadanie znalezienia dla danej funkcji jej wielomianu interpolacyjnego stopnia co najwyżej jest więc dobrze zdefiniowane, tzn. rozwiązanie istnieje i jest wyznaczone jednoznacznie. Zauważmy, że wielomian interpolacyjny jako taki nie może być wynikiem obliczeń w naszym modelu obliczeniowym. Możemy natomiast wyznaczyć jego współczynniki w wybranej bazie.
Definicja
Niech będzie bazą w przestrzeni wielomianów stopnia co najwyżej . Zadanie interpolacji wielomianowej polega na obliczeniu dla danej funkcji współczynników takich, że wielomian
interpoluje w punktach , .
Wybór bazy wielomianowej
Jak już wiemy, zadanie interpolacji Lagrange'a sprowadza się do rozwiązania układu równań liniowych. Okazuje się, że w zależności od wyboru sposobu reprezentacji naszego wielomianu (czyli od wyboru bazy wielomianowej ), układ ten może być albo bardzo łatwy do rozwiązania, albo bardzo trudny. Co więcej, jego rozwiązanie w arytmetyce może napotykać na większe bądź mniejsze trudności (w zależności np. od uwarunkowania macierzy układu, który musimy rozwiązać).
W matematyce, jeden byt może być opisany na wiele równoważnych sposobów. W numeryce, każdy z nich może mieć diametralnie różne własności numeryczne: od odporności na błędy zaokrągleń, po koszt rozwiązania.
Dlatego, optymalizacja algorytmów numerycznych zaczyna się często od wyrażenia tego samego --- inaczej.
W naturalny sposób powstaje więc problem wyboru "wygodnej" bazy w . Rozpatrzymy trzy bazy: Lagrange'a, potęgową i Newtona.
Baza Lagrange'a (kanoniczna)
Zdefiniujmy dla wielomiany
Zauważmy, że każdy z jest stopnia dokładnie oraz
Teraz widać, że wielomiany te stanowią bazę w , którą nazywamy bazą Lagrange'a. Macierz układu zadania interpolacji jest w takim wypadku identycznością i w konsekwencji , . Wielomian interpolacyjny dla funkcji można więc zapisać jako
Koszt kombinatoryczny rozwiązania zadania interpolacji jest przy tym zerowy.
Wzory barycentryczne
Przypuśćmy, że chcielibyśmy obliczyć wartość wielomianu interpolacyjnego w punkcie różnym od , . Podstawiając
oraz mamy pierwszy wzór barycentryczny
i ostatecznie dostajemy tzw. drugi wzór barycentryczny na wielomian interpolacyjny,
gdzie . W ostatniej równości wykorzystaliśmy fakt, że , co łatwo widzieć, rozpatrując zadanie interpolacji funkcji . Drugi wzór barycentryczny jest korzystniejszy w implementacji.
Dla wielu układów węzłów, wagi są zadane jawnymi wzorami, np. dla węzłów równoodległych (niezależnie od tego, na jakim odcinku!) wagi w drugim wzorze barycentrycznym wynoszą po prostu
Również dla węzłów Czebyszewa istnieją eleganckie wzory na takie współczynnki.
Można pokazać, że wartość wielomianu iterpolacyjnego obliczona w arytmetyce według pierwszego wzoru barycentrycznego spełnia
gdzie , a więc jest to algorytm numerycznie poprawny. Zachowanie drugiej postaci wzoru barycentrycznego w arytmetyce jest nieco bardziej skomplikowane.
Baza potęgowa (naturalna)
Znacznie prościej można obliczyć wartość wielomianu interpolacyjnego, (a także jego pochodnych), gdy jest on dany w najczęściej używanej bazie potęgowej, , . Jeśli bowiem
to również
co sugeruje zastosowanie następującego schematu Hornera do obliczenia :
Algorytm Algorytm Hornera
<math>v_n = a_n;</math>
for (j=n-1; j >= 0 ; j--)
<math>v_j\, = \,v_{j+1}\cdot x\,+\,a_j</math>;
Po wykonaniu tego algorytmu . Schemat Hornera wymaga wykonania tylko mnożeń i dodawań. Ma on również głębszy sens, bo jego produktem ubocznym mogą być także wartości pochodnych naszego wielomianu w . Algorytm Hornera okazuje się optymalny. Każdy inny algorytm obliczający dokładną wartość wielomianu, gdy danymi są współczynniki wielomianu, wymaga wykonania co najmniej mnożeń i dodawań. Algorytm Hornera jest też numerycznie poprawny.
Zauważmy jednak, że w przypadku bazy potęgowej macierz układu zadania interpolacji jest pełna. Jest to tzw. macierz Vandermonde'a. Obliczenie współczynników wielomianu interpolacyjnego w bazie potęgowej bezpośrednio z tego układu, stosując jedną ze znanych nam już metod, kosztowałoby rzędu operacji arytmetycznych. Co gorsza, w często spotykanym przypadku, gdy węzły interpolacji są równoodległe, ta macierz jest bardzo źle uwarunkowana!
Baza Newtona
Rozwiązaniem pośrednim, które łączy prostotę obliczenia współczynników z prostotą obliczenia wartości i ewentualnie jego pochodnych, jest wybór bazy Newtona,
W tym przypadku współczynniki rozwinięcia wielomianu interpolacyjnego będziemy oznaczać przez ,
Zwróćmy od razu uwagę na ważną własność bazy Newtona. Jeśli jest wielomianem interpolacyjnym dla funkcji opartym na węzłach , , to oraz
Wartość możemy obliczyć, stosując prostą modyfikację algorytmu Hornera:
Algorytm Algorytm Hornera dla bazy Newtona
<math>v_n = b_n;</math>
for (j=n-1; j >= 0 ; j--)
<math>v_j\, = \,v_{j+1}\cdot (x-x_j)\,+\,b_j</math>;
Ponadto układ równań zadania interpolacji jest trójkątny dolny, o specyficznej strukturze, dzięki czemu można stworzyć elegancki algorytm, który teraz przedstawimy.
Algorytm różnic dzielonych
Różnicę dzieloną funkcji opartą na różnych węzłach , gdzie , definiuje się indukcyjnie jako
Zachodzi następujące ważne twierdzenie.
Twierdzenie O różnicach dzielonych
Współczynniki wielomianu interpolacyjnego Newtona dla danej funkcji dane są przez różnice dzielone w węzłach , tzn.
Dowód
Dla , oznaczmy przez wielomian z interpolujący w węzłach . Wtedy ma miejsce następująca równość ():
Aby ją pokazać wystarczy, że prawa strona tej równości, którą oznaczymy przez , przyjmuje wartości dla , . Rzeczywiście, jeśli to
Ponadto
oraz podobnie . Stąd jest wielominem z interpolującym w węzłach , , czyli .
Dalej postępujemy indukcyjnie ze względu na stopień wielomianu interpolacyjnego. Dla mamy oczywiście . Niech . Ponieważ, jak łatwo zauważyć,
z założenia indukcyjnego mamy dla . Aby pokazać podobną równość dla , zauważmy, że
Zauważmy teraz, że jest współczynnikiem przy w wielomianie . Z założenia indukcyjnego wynika, że współczynniki przy w wielomianach i są ilorazami różnicowymi opartymi odpowiednio na węzłach i . Stąd
co kończy dowód.
Różnicę dzieloną można łatwo obliczyć na podstawie wartości , , budując następującą tabelkę:
Zauważmy przy tym, że "po drodze" obliczamy dla wszystkich , a więc w szczególności również interesujące nas różnice dzielone . Stąd i z twierdzenia o różnicach dzielonych wynika algorytm obliczania współczynników wielomianu interpolacyjnego w bazie Newtona. Po wykonaniu następującego algorytmu,
Algorytm Metoda różnic dzielonych
for (j = 0; j <= n; j++)
<math>b_j</math> = <math>f(x_j)</math>;
for (j = 1; j <= n; j++)
for (k = n; k >= j; k--)
<math>b_k</math> = <math>(b_k-b_{k-1})/(x_k - x_{k-j})</math>;
współczynniki na końcu algorytmu zawierają wspólczynniki wielomianu interpolacyjnego w bazie Newtona. Czy gdybyś zobaczył ten algorytm na samym początku tego wykładu, zgadłbyś, do czego może służyć?!
Okazuje się, że przy realizacji w algorytmu różnic dzielonych istotną rolę odgrywa porządek węzłów. Można pokazać, że --- o ile węzły są uporządkowane nierosnąco lub niemalejąco --- algorytm liczenia jest numerycznie poprawny ze względu na dane interpolacyjne , a cały algorytm różnic dzielonych daje w arytmetyce współczynniki wielomianu interpolacyjnego, będące niewiekim zaburzeniem wartości dokładnych.
Uwarunkowanie
Danymi w zadaniu interpolacji są zarówno wartości interpolowanej funkcji, jak i węzły interpolacji. Traktując węzły jako sztywno zadane parametry zadania i dopuszczając jedynie zaburzenia wartości funkcji, można pokazać, że jeśli zamiast rozpatrzyć jej zaburzenie , gdzie , to
gdzie
Znacznie rzadziej rozważa się uwarunkowanie zadania interpolacji ze względu na zaburzenie węzłów. Warto zaznaczyć, że zaburzenie danych interpolacji tylko w jednym punkcie może mieć wpływ na przebieg całego wielomianu interpolacyjnego, co ukazuje poniższy przykład:
Przykład
Pokażemy zmianę kilku bazowych wielomianów Lagrange'a stopnia 10 (dla węzłów równoodległych w ) w sytuacji, gdy trzeci węzeł interpolacji zostanie zaburzony o 0.01.

Jak widać, to lokalne zaburzenie danych może powodować wyraźne globalne zaburzenie całego wielomianu interpolacyjnego (zwróć uwagę na prawy koniec przedziału!).
MATLAB i Octave mają wbudowaną funkcję wyznaczającą wielomian, interpolujący zadane wartości: jeśli x jest wektorem zawierającym węzłów, a y --- wektorem zawierającym wartości w węzłach, to
c = polyfit(x,y,N-1);
daje współczynniki wielomianu interpolacyjnego (Ostatni argument jest równy , bo taki powinien być stopień wielomianu interpolacyjnego Lagrange'a!).
Co ciekawe (i budzące trochę zgrozy!) --- wielomian (zarówno w MATLABie, jak w Octave) jest wyznaczany w bazie naturalnej, przez rozwiązanie układu równań z macierzą Vandermonde'a, a więc w sposób najgorszy z możliwych. Nie sądzisz, że czas najwyższy, aby to zmienić? Napisz odpowiedni kod i wyślij do Octave-forge!
Aby teraz wyznaczyć wartości takiego wielomianu w zadanych punktach , także musimy użyć specjalnej funkcji,
Y = polyval(c,X);
Domyślamy się, że implementuje ona algorytm Hornera.
Przykład
Interpolujemy tabelkę
| 2 | 1 | 0 | |
| 5 | 2 | 1 |
wielomianem stopnia co najwyżej 2.
Zgodnie z przewidywaniami, otrzymaliśmy wielomian . Wartość tego wielomianu dla rzeczywiście jest równa 10.
A co się stanie, gdy będziemy szukać wielomianu stopnia niższego?
Też "coś" zostało obliczone --- wielomian (jak domyślamy się) . Nie dziwi, że ten wielomian nie jest wielomianem interpolacyjnym (dlaczego?) --- więc czym może być? Okazuje się, że to coś to wielomian nalepiej pasujący do danych w sensie aproksymacji średniokwadratowej, o czym będzie mowa w innym wykładzie.
Warto jeszcze może wiedzieć, że polyfit można także wywołać dla jeszcze wyższego stopnia wielomianu, jednak, co niespodziewane, wynikiem nie będzie wielomian stopnia 2, uzyskany poprzednio:
Wynika to stąd, że gdy dopuszczalny stopień wielomianu jest wyższy niż wymagany w zadaniu interpolacji Lagrange'a, zadanie interpolacji ma nieskończenie wiele rozwiązań. Funkcja polyfit wybiera z nich to, które spełnia warunek, że norma euklidesowa wektora współczynników wielomianu jest najmniejsza z możliwych.
Pragnąc wykorzystać interpolację we własnym programie w C, najlepiej samemu zaprogramować bądź drugi wzór barycentryczny, bądź algorytm różnic dzielonych --- w zależności od potrzeb.
Przypadek węzłów wielokrotnych
Uogólnieniem rozpatrzonego zadania interpolacji jest zadanie interpolacji Hermite'a. Zakładamy, że oprócz (różnych) węzłów dane są również ich krotności , , przy czym . Należy skonstruować wielomian taki, że
Oczywiście zakładamy przy tym, że odpowiednie pochodne funkcji istnieją.
Lemat
Zadanie interpolacji Hermite'a ma jednoznaczne rozwiązanie.
Dowód
Istnienie i jednoznaczność rozwiązania można uzasadnić tak samo jak w przypadku węzłów jednokrotnych. Przedstawiając wielomian w dowolnej bazie otrzymujemy układ równań z niewiadomymi, który dla zerowej prawej strony ma jedynie rozwiązanie zerowe. Inaczej bowiem istniałby wielomian niezerowy stopnia nie większego niż , który miałby zera o łącznej krotności większej niż .
Nas oczywiście interesuje konstrukcja wielomianu . W tym celu ustawimy węzły w ciąg
i zdefiniujemy uogólnioną bazę Newtona w jako
Uogólnimy również pojęcie różnicy dzielonej na węzły powtarzające się, kładąc
dla , oraz
dla . Zauważmy, że przy tej definicji różnice możemy łatwo obliczyć stosując schemat podobny do tego z przypadku węzłów jednokrotnych.
Twierdzenie O różnicach dzielonych dla interpolacji Hermite'a
Współczynniki wielomianu interpolacyjnego Hermite'a w bazie Newtona,
dane są przez odpowiednie różnice dzielone, tzn.
Dowód
Dowód przeprowadzimy podobnie jak dla węzłów jednokrotnych. Niech oznacza wielomian interpolacyjny Hermite'a oparty na (być może powtarzających się) węzłach . To znaczy, interpoluje w węzłach takich, że występuje w ciągu , a jego krotność jest liczbą powtórzeń w tym ciągu.
Zauważmy najpierw, że dla zachodzi znany nam już wzór,
Rzeczywiście, oznaczmy przez prawą stronę powyższej równości. Dla mniejszego od krotności danego węzła w ciągu , mamy , a ponieważ
to
Korzystając z tego wzoru sprawdzamy, że spełnia odpowiednie warunki interpolacyjne, a stąd .
Dalej postępujemy indukcyjnie ze względu na . Dla mamy . Dla wystarczy pokazać, że . W tym celu rozpatrzymy dwa przypadki.
Jeśli , to mamy jeden węzeł o krotności . Wielomian interpolacyjny jest wtedy postaci
a stąd . Jeśli zaś , to równość wynika z wcześniej wyprowadzonych wzorów oraz z założenia indukcyjnego.
Uwaga
Zauważmy, ze pojęcie różnicy dzielonej formalnie zdefiniowaliśmy jedynie dla ciągu węzłów postaci , gdzie są parami różne. Tą definicję można rozszerzyć do dowolnego ciągu węzłów. Można bowiem powiedzieć, że jest współczynnikiem przy wielomianu interpolującego w węzłach (uwzględniając krotności). Równoważnie,
Błąd interpolacji
Gdy mamy do czynienia z funkcją, która jest "skomplikowana", często dobrze jest zastąpić ją funkcją "prostszą". Mówimy wtedy o aproksymacji funkcji. Funkcję musimy również aproksymać wtedy, gdy nie jesteśmy w stanie uzyskać pełnej o niej informacji. Na przykład, gdy funkcja reprezentuje pewien proces fizyczny, często zdarza się, że dysponujemy jedynie ciągiem próbek, czyli wartościami tej funkcji w pewnych punktach. Jasne jest, że chcielibyśmy przy tym, aby błąd aproksymacji był możliwie mały.
Podobnie ma się sprawa w przypadku implementacji funkcji elementarnych (.) w bibliotece funkcji matematycznych, czy wręcz w procesorze. Tam również najchętniej poszukiwalibyśmy sposobu taniego przybliżenia wartości dokładnej funkcji. I rzeczywiście, często w tym celu stosuje się m.in. specjalnie konstruowaną aproksymację wielomianową.
Z tego punktu widzenia, intepolacja wielomianowa może być traktowana jako jeden ze sposobów aproksymacji funkcji, opartym na próbkowaniu. Naturalnym staje się więc pytanie o błąd takiej aproksymacji.
Niech będą (niekoniecznie różnymi) węzłami należącymi do pewnego (być może nieskończonego) przedziału . Dla danej funkcji , przez rozważamy, tak jak w całym wykładzie, wielomian interpolacyjny stopnia co najwyżej interpolujący w zadanych węzłach. W przypadku węzłów wielokrotnych jest to oczywiście wielomian interpolacyjny Hermite'a; gdy węzły są jednokrotne, mamy do czynienia z interpolacją Lagrange'a.
Lemat Postać błędu interpolacji
Dla dowolnego punktu błąd interpolacji w wyraża się wzorem
Jeśli ponadto , czyli pochodna w istnieje i jest ciągła, to
gdzie jest pewnym punktem należącym do najmniejszego przedziału zawierającego punkty .
Dowód
Możemy założyć, że nie jest żadnym z węzłów , . Niech będzie wielomianem interpolacyjnym funkcji opartym na węzłach i dodatkowo na węźle . Mamy wtedy
a ponieważ z warunku interpolacyjnego , to mamy też pierwszą równość w lemacie.
Aby pokazać drugą część lematu, rozpatrzmy funkcję ,
Z warunków interpolacyjnych na wynika, że funkcja ma punkty zerowe o łącznej krotności co najmniej . Wykorzystując twierdzenie Rolle'a wnioskujemy stąd, że ma zera o łącznej krotności co najmniej , ma zera o łącznej krotności co najmniej , itd. W końcu funkcja zeruje się w co najmniej jednym punkcie należącym do najmniejszego przedziału zawierającego . Wobec tego, że , a -sza pochodna wielomianu wynosi , mamy
Stąd
Zwykle interesuje nas nie tyle błąd w ustalonym punkcie , ale na całym przedziale . Zakładając teraz, że przedział jest domknięty, czyli
dla pewnych , błąd ten będziemy mierzyć w normie jednostajnej (Czebyszewa). Dla funkcji ciągłej , norma ta jest zdefiniowana jako
Niech , gdzie , będzie klasą funkcji
gdzie . Mamy następujące twiedzenie.
Twierdzenie O najgorszym możliwym błędzie interpolacji w klasie
Załóżmy, że każdą funkcję aproksymujemy jej wielomianem interpolacyjnym opartym na węzłach . Wtedy maksymalny błąd takiej aproksymacji wynosi
Dowód
Oszacowanie górne wynika bezpośrednio z lematu o postaci błędu interpolacji, bowiem dla mamy
Z drugiej strony zauważmy, że dla wielomianu mamy oraz
Zjawisko Rungego i dobór węzłów interpolacji
Rozważmy zadanie interpolacji funkcji
w równoodległych węzłach na przedziale . Okazuje się, że dla dużych wartości , wielomian interpolacyjny ma poważne kłopoty z aproksymacją tej funkcji przy krańcach przedziału:
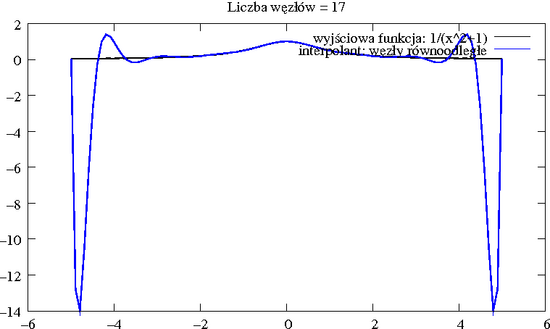
Z kolei wielomian oparty na węzłach Czebyszewa znacznie lepiej przybliża tę funkcję.
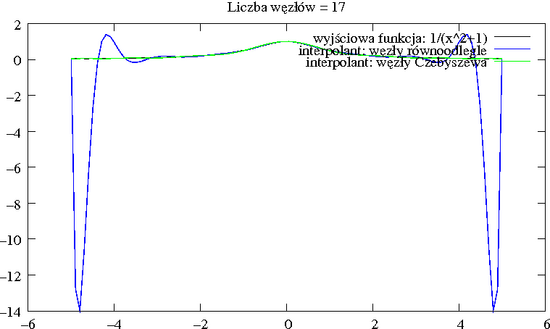
Rzeczywiście, węzły Czebyszewa zagęszczają się w pobliżu krańców odcinka.
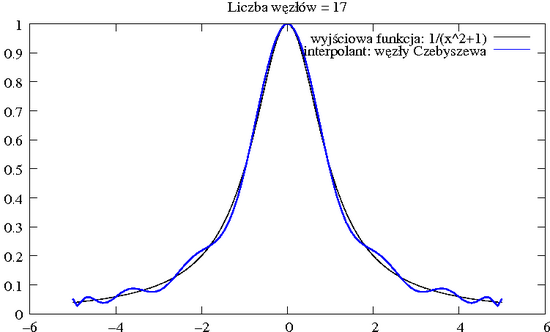
Wiąże się to z zachowaniem się samych wielomianów bazowych: wielomiany oparte na węzłach równoodległych właśnie silnie oscylują w pobliżu krańców przedziału (jasne: nasz wielomian jest wysokiego stopnia, musi mieć dużo zer, a z drugiej strony, jako wielomian wysokiego stopnia, chce szybko uciec do nieskończoności, dlatego "wije się" jak może). Natomiast wielomiany bazowe oparte na węzłach Czebyszewa są najspokojniejsze: wiją się, ale z umiarem, bo zagęszczone przy krańcach węzły skutecznie je "duszą".
Zauważmy, że błąd aproksymacji
w istotny sposób
zależy od wyboru węzłów . Naturalne jest więc
teraz następujące pytanie: w których punktach
przedziału należy obliczać wartości funkcji,
aby błąd był minimalny? Problem ten sprowadza się
oczywiście do minimalizacji wielkości
względem węzłów .
Twierdzenie O optymalnym doborze węzłów
Błąd aproksymacji w klasie funkcji jest minimalny gdy węzły interpolacji są zadane jako węzły Czebyszewa na , tzn.
Ponadto, dla optymalnych węzłów mamy
Dowód tego twierdzenia opiera się na własnościach pewnego ważnego ciągu wielomianów, który teraz przedstawimy.
Wielomiany Czebyszewa
Ciąg wielomianów Czebyszewa (pierwszego rodzaju) zdefiniowany jest indukcyjnie jako

Zobacz biografię
Zauważmy, że jest wielomianem stopnia dokładnie o współczynniku przy równym (). Ponadto wielomian można dla przedstawić w postaci
Rzeczywiście, łatwo sprawdzić, że jest to prawdą dla . Stosując podstawienie , , oraz wzór na sumę cosinusów otrzymujemy dla
co jest równoważne formule rekurencyjnej dla .

Ze wzoru wynikają również inne ważne własności wielomianów Czebyszewa. Norma wielomianu Czebyszewa na wynosi
i jest osiągana w punktach tego przedziału równych
przy czym .
W końcu, -ty wielomian Czebyszewa ma dokładnie pojedynczych zer w równych
Miejsca zerowe wielomianu Czebyszewa będziemy nazywać węzłami Czebyszewa. Konsekwencją wymienionych własności jest następująca własność ekstremalna wielomianów Czebyszewa.
Przez oznaczymy klasę wielomianów stopnia o współczynniku wiodącym równym , tzn.
Twierdzenie O minimaksie
Niech . W klasie minimalną normę jednostajną na przedziale ma wielomian , tzn.

Możemy teraz przeprowadzić dowód twierdzenia o optymalnym doborze węzłów:
Dowód
Dowód wynika teraz bezpośrednio z twierdzenia o minimaksie. Zauważmy bowiem, że wielomian jest w klasie . Stąd dla optymalnymi węzłami są zera wielomianu Czebyszewa, przy których
Jeśli przedział jest inny niż , należy dokonać liniowej zamiany zmiennych tak, aby przeszedł on na . Bezpośrednie sprawdzenie pokazuje, że w klasie minimalną normę Czebyszewa na przedziale ma wielomian
Stąd
Wielomiany Czebyszewa znajdują bardzo wiele, czasem zaskakujących, zastosowań w różnych działach numeryki, m.in. w konstrukcji metod iteracyjnych rozwiązywania równań liniowych.
Równie interesujący jest fakt, że wielomian interpolacyjny oparty na węzłach Czebyszewa jest prawie optymalnym przybliżeniem wielomianowym zadanej funkcji:
Twierdzenie Jacksona, o prawie optymalnej interpolacji w węzłach Czebyszewa
Dla , wielomian interpolacyjny stopnia co najwyżej , oparty na węzłach Czebyszewa, spełnia
gdzie jest wielomianem stopnia co najwyżej , najlepiej aproksymującym w sensie normy jednostajnej.
Jeśli więc , to wielomian oparty na węzłach Czebyszewa jest co najwyżej 3.02 razy, a gdy --- maksymalnie 4 razy gorszy od optymalnego. Można więc powiedzieć, że jest prawie optymalny.
Literatura
W celu dogłębnego zapoznania się z omawianym na wykładzie materiałem, przeczytaj rozdział 6.1--6.3 w
- D. Kincaid, W. Cheney Analiza numeryczna, Wydawnictwa Naukowo-Techniczne, Warszawa 2006, ISBN 83-204-3078-X.