Logika i teoria mnogości/Wykład 1: Po co nam teoria mnogości? Naiwna teoria mnogości, naiwna indukcja, naiwne dowody niewprost: Różnice pomiędzy wersjami
m →"Naiwna" teoria mnogości: literowka: odmiana Cantora |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| (Nie pokazano 16 wersji utworzonych przez 2 użytkowników) | |||
| Linia 14: | Linia 14: | ||
teorią mnogości. | teorią mnogości. | ||
[[grafika:Fraenkel.jpg|thumb|right||Adolf Abraham Halevi Fraenkel (1891-1965) <br>[[Biografia Fraenkel|Zobacz biografię]]]]Teoria matematyczna nie może dopuszczać istnienia paradoksów i dlatego na początku XX wieku zmieniono podejście do teorii mnogości. | [[grafika:Fraenkel.jpg|thumb|right||Adolf Abraham Halevi Fraenkel (1891-1965) <br>[[Biografia Fraenkel|Zobacz biografię]]]]Teoria matematyczna nie może dopuszczać istnienia paradoksów i dlatego na początku XX wieku zmieniono podejście do teorii mnogości. Zaproponowany przez [[Biografia_Zermelo|Ernsta Zermelo]] i uzupełniony przez [[Biografia_Fraenkel|Adolfa Abrahama Halevi Fraenkela]] system aksjomatów wyklucza paradoksy, które spowodowały, że naiwna teoria zbiorów musiała zostać porzucona. Aksjomaty te nakładają pewne ograniczenia na konstrukcje zaproponowane przez [[Biografia_Cantor|Georga Cantora]]. W większości przypadków jednak intuicje związane z naiwną teorią mnogości sprawdzają się również w aksjomatycznej teorii zbiorów. Zaprezentowane poniżej, skrótowe przedstawienie "naiwnej teorii mnogości" ma na celu wyrobienie intuicji niezbędnych przy dalszej pracy nad formalną wersją tych teorii. Aksjomatyczna teoria zbiorów zostanie przedstawiona w [[Logika i teoria mnogości/Wykład 4: Teoria mnogości ZFC. Operacje na zbiorach|Wykładzie 4.]] | ||
W podejściu zaproponowanym przez [[Biografia_Cantor|Georga Cantora]] | W podejściu zaproponowanym przez [[Biografia_Cantor|Georga Cantora]] zbiory skończone można łatwo wskazywać poprzez wyliczenie ich elementów. Definiowanie zbiorów nieskończonych wymaga bardziej rozwiniętego języka, niemniej jednak, według [[Biografia_Cantor|Georga Cantora]], każda kolekcja obiektów jest zbiorem. Podstawowym symbolem używanym przy definiowaniu i opisywaniu zbiorów jest | ||
<center><math> | <center><math> | ||
\in | \in | ||
</math></center> | </math></center> | ||
| Linia 25: | Linia 25: | ||
Napis | Napis | ||
<center> "Kraków" <math> \in </math> "zbiór wszystkich miast Polski" </center> | <center> "Kraków" <math>\in</math> "zbiór wszystkich miast Polski" </center> | ||
ilustruje zastosowanie tego symbolu. | ilustruje zastosowanie tego symbolu. | ||
| Linia 35: | Linia 35: | ||
Zbiór | Zbiór | ||
<center><math> | <center><math> | ||
\{2,3 | \{2,3</math> Kraków <math>\} | ||
</math></center> | </math></center> | ||
posiada trzy elementy. Liczba '''2''' jest elementem tego zbioru | posiada trzy elementy. Liczba '''2''' jest elementem tego zbioru | ||
<math>2\in\{2,3 | <math>2\in\{2,3</math> Kraków <math>\}</math>, ale również<br/> | ||
Kraków <math>\in\{2,3 | Kraków <math>\in\{2,3</math>, Kraków<math>\}</math>. | ||
| Linia 49: | Linia 49: | ||
<math>\{2,2,3\}</math>, a więc | <math>\{2,2,3\}</math>, a więc | ||
<center><math> | <center><math> | ||
\{2,3\} = \{2,3,3\} | \{2,3\} = \{2,3,3\}</math></center> | ||
</math></center> | |||
Podobnie <math>\{2,3\}=\{3,2\}</math> i | Podobnie <math>\{2,3\}=\{3,2\}</math> i | ||
<center><math> | <center><math> | ||
\{2,3\}= </math> "zbiór liczb naturalnych ściśle pomiędzy '''1''' a | \{2,3\}=</math> "zbiór liczb naturalnych ściśle pomiędzy '''1''' a | ||
'''4'''". | '''4'''". | ||
</center> | </center> | ||
| Linia 66: | Linia 65: | ||
[[grafika:Cantor.jpg|thumb|right||Georg Ferdinand Ludwig Philipp Cantor (1845-1918) <br>[[Biografia Cantor|Zobacz biografię]]]]Zbiory można definiować na wiele sposobów. Najprostszym sposobem zdefiniowania zbioru jest wyliczenie jego elementów. Strategia ta zawodzi jednak w odniesieniu do zbiorów nieskończonych -- nie jesteśmy w stanie wypisać wszystkich liczb naturalnych. Zgodnie z postulatami [[Biografia_Cantor|Georga Cantora]] możemy przyjąć, że istnieje zbiór wszystkich liczb naturalnych. Czasami, na określenie zbiorów nieskończonych używamy nieformalnego zapisu - zbiór wszystkich liczb naturalnych może być zapisany jako | [[grafika:Cantor.jpg|thumb|right||Georg Ferdinand Ludwig Philipp Cantor (1845-1918) <br>[[Biografia Cantor|Zobacz biografię]]]]Zbiory można definiować na wiele sposobów. Najprostszym sposobem zdefiniowania zbioru jest wyliczenie jego elementów. Strategia ta zawodzi jednak w odniesieniu do zbiorów nieskończonych -- nie jesteśmy w stanie wypisać wszystkich liczb naturalnych. Zgodnie z postulatami [[Biografia_Cantor|Georga Cantora]] możemy przyjąć, że istnieje zbiór wszystkich liczb naturalnych. Czasami, na określenie zbiorów nieskończonych używamy nieformalnego zapisu - zbiór wszystkich liczb naturalnych może być zapisany jako | ||
<center><math> | <center><math> | ||
\{0,1,2,3,4,\ldots\} | \{0,1,2,3,4,\ldots\}</math></center> | ||
</math></center> | |||
W podejściu zaproponowanym przez [[Biografia_Cantor|Georga Cantora]] równoważna definicja tego | W podejściu zaproponowanym przez [[Biografia_Cantor|Georga Cantora]] równoważna definicja tego | ||
| Linia 79: | Linia 77: | ||
zdefiniować w sposób następujący | zdefiniować w sposób następujący | ||
<center><math> | <center><math> | ||
\{x\,|\, x</math> jest liczbą parzystą <math> \} | \{x\,|\, x</math> jest liczbą parzystą <math>\}</math></center> | ||
</math></center> | |||
Bardziej ogólnie | Bardziej ogólnie | ||
<center><math> | <center><math> | ||
\{x\,|\ | \{x\,|\ </math> warunek. <math>\} | ||
</math></center> | </math></center> | ||
W skład powyżej zdefiniowanego zbioru wchodzą te elementy, które | W skład powyżej zdefiniowanego zbioru wchodzą te elementy, które | ||
spełniają warunek występujący po znaku <math>\,|\ | spełniają warunek występujący po znaku <math>\,|\ </math>,. Żeby | ||
zakwalifikować element do powyższego zbioru, wstawiamy go w miejsce | zakwalifikować element do powyższego zbioru, wstawiamy go w miejsce | ||
<math>x</math> w warunku występującym po <math>\,|\ | <math>x</math> w warunku występującym po <math>\,|\ </math>, i sprawdzamy, czy jest on | ||
prawdziwy. Żeby pokazać, że | prawdziwy. Żeby pokazać, że | ||
<center><math> | <center><math> | ||
2\in\{x\,|\, x</math> jest liczbą parzystą <math> \} | 2\in\{x\,|\, x</math> jest liczbą parzystą <math>\}</math>,</center> | ||
</math></center> | |||
musimy dowieść, że warunek "'''2''' jest liczbą parzystą" jest | musimy dowieść, że warunek "'''2''' jest liczbą parzystą" jest | ||
| Linia 110: | Linia 106: | ||
następujący sposób | następujący sposób | ||
<center><math> | <center><math> | ||
\{x\,|\, x</math> jest liczbą parzystą <math> \}\subseteq </math> "zbiór | \{x\,|\, x</math> jest liczbą parzystą <math>\}\subseteq</math> "zbiór | ||
liczb naturalnych" <math> | liczb naturalnych" <math></math></center> | ||
</math></center> | |||
Ogólniej, jeśli każdy element zbioru <math>A</math> jest elementem zbioru <math>B</math> | Ogólniej, jeśli każdy element zbioru <math>A</math> jest elementem zbioru <math>B</math> | ||
mówimy, że zbiór <math>A</math> jest podzbiorem zbioru <math>B</math> i piszemy | mówimy, że zbiór <math>A</math> jest podzbiorem zbioru <math>B</math> i piszemy | ||
<center><math> | <center><math> | ||
A\subseteq B | A\subseteq B</math></center> | ||
</math></center> | |||
W takim przypadku mówimy, że pomiędzy zbiorami <math>A</math> i <math>B</math> zachodzi | W takim przypadku mówimy, że pomiędzy zbiorami <math>A</math> i <math>B</math> zachodzi | ||
| Linia 130: | Linia 124: | ||
ten możemy zapisać formalnie w następujący sposób | ten możemy zapisać formalnie w następujący sposób | ||
<center><math> | <center><math> | ||
A = B | A = B</math> wtedy i tylko wtedy, kiedy <math>A\subseteq B</math> i <math> | ||
B\subseteq A | B\subseteq A</math></center> | ||
</math></center> | |||
Często zależy nam na określeniu znaczącym, że jeden zbiór jest | Często zależy nam na określeniu znaczącym, że jeden zbiór jest | ||
| Linia 139: | Linia 132: | ||
wtedy symbolu <math>\varsubsetneq</math> w następujący sposób | wtedy symbolu <math>\varsubsetneq</math> w następujący sposób | ||
<center><math> | <center><math> | ||
A\varsubsetneq B </math> wtedy i tylko wtedy, kiedy <math> ( | A\varsubsetneq B</math> wtedy i tylko wtedy, kiedy <math>( | ||
A\subseteq B </math> i nieprawda, że <math> A=B) | A\subseteq B</math> i nieprawda, że <math>A=B) | ||
</math></center> | </math></center> | ||
| Linia 168: | Linia 161: | ||
zbioru <math>B</math> i żadne elementy spoza tych zbiorów | zbioru <math>B</math> i żadne elementy spoza tych zbiorów | ||
<center><math> | <center><math> | ||
A\cup B = \{x\,|\, x\in A | A\cup B = \{x\,|\, x\in A</math> lub <math>x\in B\}</math></center> | ||
</math></center> | |||
[[File:Logika-1.1.svg|300x150px|thumb|center|Unia zbiorów.]]Podobnie definiujemy przecięcie zbiorów | |||
<center><math> | |||
A\cap B = \{x\,|\, x\in A</math> i <math>x\in B\}</math></center> | |||
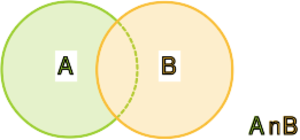
[[File:Logika-1.2.svg|500x180px|thumb|center|Standardowy obrazek ilustrujący przecięcie zbiorów oraz różnicę zbiorów.]] | |||
< | <center><math> | ||
A\setminus B = \{x\,|\, x\in A</math> i <math>x\notin B\}</math></center> | |||
< | |||
[[File:Logika-1.3.svg|300x150px|thumb|center|Standardowy obrazek ilustrujący różnicę zbiorów.]]{{cwiczenie|1.2|| | |||
{{cwiczenie|1.2|| | |||
Dla następujących par zbiorów ustal zawieranie lub równość | Dla następujących par zbiorów ustal zawieranie lub równość | ||
# <math>A= </math> "zbiór liczb naturalnych" <math> \setminus\{x\,|\ | # <math>A=</math> "zbiór liczb naturalnych" <math>\setminus\{x\,|\ </math> liczba nieparzysta, większa niż '''2''' dzieli <math>x \}</math> <br/>i drugi zbiór <math>B=\{2^n\,|\ </math> gdzie <math>n</math> jest liczbą naturalną <math>\}</math>, | ||
# <math>A=\{x\,|\ | # <math>A=\{x\,|\ </math> liczba '''2''' dzieli <math>x \}\cup\{x\,|\ </math> liczba '''3''' dzieli <math>x \}</math> i zbiór <math>B=\{x\,|\ </math> liczba '''6''' dzieli <math>x \}</math>. | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
# Każda liczba postaci <math>{2^n}</math> jest liczbą naturalną niepodzielną przez żadną liczbę nieparzystą większą niż '''2''', a więc <math>B\subseteq A</math>. Każda liczba naturalna, która nie dzieli się przez żadną liczbę nieparzystą posiada tylko jeden dzielnik pierwszy '''2'''. W związku z tym każda z liczb w <math>\ | # Każda liczba postaci <math>{2^n}</math> jest liczbą naturalną niepodzielną przez żadną liczbę nieparzystą większą niż '''2''', a więc <math>B\subseteq A</math>. Każda liczba naturalna, która nie dzieli się przez żadną liczbę nieparzystą posiada tylko jeden dzielnik pierwszy '''2'''. W związku z tym każda z liczb w <math>\text{A}</math> występuje również w <math>B</math>. W związku z tym <math>A=B</math>. | ||
# Każda liczba, która jest podzielna przez '''6''', dzieli się również przez '''2''', co dowodzi, że <math>B\subseteq A</math>. Zawieranie w drugą stronę nie zachodzi, ponieważ liczba <math>9\in A</math> i <math>9\notin B</math>. | # Każda liczba, która jest podzielna przez '''6''', dzieli się również przez '''2''', co dowodzi, że <math>B\subseteq A</math>. Zawieranie w drugą stronę nie zachodzi, ponieważ liczba <math>9\in A</math> i <math>9\notin B</math>. | ||
</div></div> | </div></div> | ||
Dla dowolnego zbioru <math>\ | Dla dowolnego zbioru <math>\text{A}</math> zachodzi <math>A\cup A = A</math> i <math>A\cap A = A</math>. Zbiór, który otrzymujemy jako wynik operacji <math>A\setminus A</math> jest ''zbiorem pustym''. Na mocy definicji różnicy zbiorów elementami zbioru <math>A\setminus A</math> są wyłącznie te elementy <math>A</math>, które nie należą do <math>A</math>. Takie elementy nie istnieją - żaden element ze zbioru <math>A</math> nie należy do <math>A\setminus A</math> i żaden element spoza <math>A</math> nie należy do tego zbioru. Zbiór pusty jest oznaczany przez <math>\emptyset</math>. Odejmowanie zbiorów od samych siebie nie jest jedynym sposobem na otrzymanie zbioru pustego. | ||
<center><math> | <center><math> | ||
\{1,2,2006\}\setminus </math> "zbiór liczb naturalnych" <math> = </math> "zbiór psów" <math> \setminus </math> "zbiór wszystkich zwierząt" </center> | \{1,2,2006\}\setminus</math> "zbiór liczb naturalnych" <math>=</math> "zbiór psów" <math>\setminus</math> "zbiór wszystkich zwierząt" </center> | ||
Zbiór po lewej stronie nierówności jest równy zbiorowi po prawej stronie nierówności. Każdy element zbioru po prawej stronie jest również elementem zbioru po lewej stronie nierówności i vice versa, dlatego że żaden z tych zbiorów nie posiada elementów. | Zbiór po lewej stronie nierówności jest równy zbiorowi po prawej stronie nierówności. Każdy element zbioru po prawej stronie jest również elementem zbioru po lewej stronie nierówności i vice versa, dlatego że żaden z tych zbiorów nie posiada elementów. | ||
| Linia 219: | Linia 197: | ||
[[grafika:Frege.jpg|thumb|right||Friedrich Ludwig Gottlob Frege (1848-1925)<br>[[Biografia Frege|Zobacz biografię]]]]Niestety, podejście zaproponowane przez [[Biografia_Cantor|Georga Cantora]] i uściślone przez [[Biografia_Frege|Friedricha Frege]] posiada błędy. Jedną z pierwszych osób które zwróciły uwagę na niedociągnięcia tej teorii jest [[Biografia_Russell|Bertrand Russell]]. Zgodnie z zasadami zaproponowanymi przez [Biografia_Cantor|Georga Cantora]] można zdefiniować dowolny zbiór. Zdefiniujmy, więc zbiór | [[grafika:Frege.jpg|thumb|right||Friedrich Ludwig Gottlob Frege (1848-1925)<br>[[Biografia Frege|Zobacz biografię]]]]Niestety, podejście zaproponowane przez [[Biografia_Cantor|Georga Cantora]] i uściślone przez [[Biografia_Frege|Friedricha Frege]] posiada błędy. Jedną z pierwszych osób które zwróciły uwagę na niedociągnięcia tej teorii jest [[Biografia_Russell|Bertrand Russell]]. Zgodnie z zasadami zaproponowanymi przez [Biografia_Cantor|Georga Cantora]] można zdefiniować dowolny zbiór. Zdefiniujmy, więc zbiór | ||
<center><math> | <center><math> | ||
Z = \{A\,|\, A\notin A\} | Z = \{A\,|\, A\notin A\}</math></center> | ||
</math></center> | |||
Zbiór <math>Z</math> składa się ze zbiorów, które nie są swoimi własnymi elementami. Paradoks zaproponowany przez [[Biografia_Russell|Bertranda Russella]] polega na tym, że pytanie czy <math>Z</math> jest swoim własnym elementem prowadzi do sprzeczności. Jeśli <math>Z\in Z</math> to, zgodnie z definicją zbioru <math>Z</math> otrzymujemy <math>Z\notin Z</math>, co jest sprzecznością z założeniem. Jeśli <math>Z\notin Z</math>, to <math>Z</math> spełnia warunek na przynależność do <math>Z</math> i w związku z tym <math>Z\in Z</math>, co jest kolejną sprzecznością. Definicja zbioru zaproponowana przez [[Biografia_Cantor|Georga Cantora]] prowadzi do powstania logicznych paradoksów. Okazuje się, że pytanie: co jest zbiorem, jest trudniejsze niż wydawało się matematykom końca XIX wieku. | Zbiór <math>Z</math> składa się ze zbiorów, które nie są swoimi własnymi elementami. Paradoks zaproponowany przez [[Biografia_Russell|Bertranda Russella]] polega na tym, że pytanie czy <math>Z</math> jest swoim własnym elementem prowadzi do sprzeczności. Jeśli <math>Z\in Z</math> to, zgodnie z definicją zbioru <math>Z</math> otrzymujemy <math>Z\notin Z</math>, co jest sprzecznością z założeniem. Jeśli <math>Z\notin Z</math>, to <math>Z</math> spełnia warunek na przynależność do <math>Z</math> i w związku z tym <math>Z\in Z</math>, co jest kolejną sprzecznością. Definicja zbioru zaproponowana przez [[Biografia_Cantor|Georga Cantora]] prowadzi do powstania logicznych paradoksów. Okazuje się, że pytanie: co jest zbiorem, jest trudniejsze niż wydawało się matematykom końca XIX wieku. | ||
| Linia 256: | Linia 233: | ||
* Jeśli hipoteza jest prawdą dla <math>n</math>, to znaczy że suma pierwszych <math>n</math> liczb nieparzystych równa się <math>{n^2}</math>. Bardziej formalnie | * Jeśli hipoteza jest prawdą dla <math>n</math>, to znaczy że suma pierwszych <math>n</math> liczb nieparzystych równa się <math>{n^2}</math>. Bardziej formalnie | ||
<center><math> | <center><math> | ||
1+3+\dotsb+(2n-1) = n^2 | 1+3+\dotsb+(2n-1) = n^2 | ||
</math></center> | </math></center> | ||
| Linia 262: | Linia 239: | ||
tak więc suma pierwszych <math>{n+1}</math> liczb nieparzystych <math>1+3+\dotsb+(2n-1)+(2(n+1)-1)</math>, przy użyciu założenia powyżej może być zapisana jako | tak więc suma pierwszych <math>{n+1}</math> liczb nieparzystych <math>1+3+\dotsb+(2n-1)+(2(n+1)-1)</math>, przy użyciu założenia powyżej może być zapisana jako | ||
<center><math> | <center><math> | ||
1+3+\dotsb+(2n-1)+(2(n+1)-1) = n^2 +(2(n+1)-1)= n^2+2n+1= | 1+3+\dotsb+(2n-1)+(2(n+1)-1) = n^2 +(2(n+1)-1)= n^2+2n+1= | ||
{(n+1)}^2 | {(n+1)}^2</math></center> | ||
</math></center> | |||
Krok indukcyjny został dowiedziony. | Krok indukcyjny został dowiedziony. | ||
| Linia 278: | Linia 254: | ||
:* Dla <math>n=1</math> mamy <math>\frac{1}{2}\cdot 1\cdot 2 = 1</math>. | :* Dla <math>n=1</math> mamy <math>\frac{1}{2}\cdot 1\cdot 2 = 1</math>. | ||
:* Zakładamy, że wzór jest prawdziwy dla <math>\ | :* Zakładamy, że wzór jest prawdziwy dla <math>\text{n}</math>. W związku z tym do sumy | ||
<center><math> | <center><math> | ||
1+2+\dotsb+n+(n+1) = | 1+2+\dotsb+n+(n+1) = | ||
</math></center> | </math></center> | ||
| Linia 286: | Linia 262: | ||
:stosujemy założenie indukcyjne | :stosujemy założenie indukcyjne | ||
<center><math> | <center><math> | ||
(1+2+\dotsb+n ) +(n+1) = \frac{1}{2}n(n+1) + (n+1) = | (1+2+\dotsb+n ) +(n+1) = \frac{1}{2}n(n+1) + (n+1) = | ||
</math></center> | </math></center> | ||
| Linia 292: | Linia 268: | ||
:i po paru prostych przekształceniach otrzymujemy | :i po paru prostych przekształceniach otrzymujemy | ||
<center><math> | <center><math> | ||
= \frac{1}{2}n(n+1) +\frac{1}{2}2(n+1) = \frac{1}{2}(n+1)(n+2) | = \frac{1}{2}n(n+1) +\frac{1}{2}2(n+1) = \frac{1}{2}(n+1)(n+2)</math>,</center> | ||
</math></center> | |||
:co dowodzi kroku indukcyjnego. | :co dowodzi kroku indukcyjnego. | ||
| Linia 312: | Linia 287: | ||
:* Dla <math>n=1</math> mamy <math>\frac{1}{6}\cdot 1\cdot 2\cdot 3 = 1</math> co dowodzi podstawy indukcji. | :* Dla <math>n=1</math> mamy <math>\frac{1}{6}\cdot 1\cdot 2\cdot 3 = 1</math> co dowodzi podstawy indukcji. | ||
:* Zakładamy że wzór jest prawdziwy dla <math>\ | :* Zakładamy że wzór jest prawdziwy dla <math>\text{n}</math> to jest, że | ||
<center><math> | <center><math> | ||
1^2+2^2+\dotsb+n^2 = \frac{1}{6}n(n+1)(2n+1) | 1^2+2^2+\dotsb+n^2 = \frac{1}{6}n(n+1)(2n+1)</math></center> | ||
</math></center> | |||
:Korzystając z tego faktu przekształcamy | :Korzystając z tego faktu przekształcamy | ||
<center><math> | <center><math> | ||
1^2+2^2+\dotsb+n^2 + {(n+1)}^2= \frac{1}{6}n(n+1)(2n+1) + {(n+1)}^2 = | 1^2+2^2+\dotsb+n^2 + {(n+1)}^2= \frac{1}{6}n(n+1)(2n+1) + {(n+1)}^2 = | ||
</math></center> | </math></center> | ||
| Linia 326: | Linia 300: | ||
:i dalej do | :i dalej do | ||
:<math> | :<math> | ||
\frac{1}{6}(n+1)\left(n(2n+1)+6(n+1)\right)=\frac{1}{6}(n+1)(2n^2+7n+6)=</math><math> \frac{1}{6}(n+1)(n+2)(2(n+1)+1) | \frac{1}{6}(n+1)\left(n(2n+1)+6(n+1)\right)=\frac{1}{6}(n+1)(2n^2+7n+6)=</math><math>\frac{1}{6}(n+1)(n+2)(2(n+1)+1)</math>, | ||
</math> | |||
:co dowodzi kroku indukcyjnego. | :co dowodzi kroku indukcyjnego. | ||
| Linia 348: | Linia 321: | ||
:* Dla <math>{n=1}</math> mamy <math>3^{2n-1} + 1 = 3^1 +1 = 4</math> jest podzielne przez '''4'''. | :* Dla <math>{n=1}</math> mamy <math>3^{2n-1} + 1 = 3^1 +1 = 4</math> jest podzielne przez '''4'''. | ||
:* Zakładamy, że podzielność zachodzi dla <math>\ | :* Zakładamy, że podzielność zachodzi dla <math>\text{n}</math>. Pokażemy że <math>3^{2(n+1)-1}+1</math> jest podzielne przez '''4'''. Przekształcamy | ||
<center><math> | <center><math> | ||
3^{2(n+1)-1}+1 = 3^{2n-1+2} + 1 = 9\cdot 3^{2n-1} + 1= | 3^{2(n+1)-1}+1 = 3^{2n-1+2} + 1 = 9\cdot 3^{2n-1} + 1= | ||
</math></center> | </math></center> | ||
| Linia 357: | Linia 330: | ||
<center><math> | <center><math> | ||
=9\cdot (3^{2n-1} +1 -1) + 1 = 9\cdot (3^{2n-1} +1 -1) + 1 = | =9\cdot (3^{2n-1} +1 -1) + 1 = 9\cdot (3^{2n-1} +1 -1) + 1 = | ||
9\cdot (3^{2n-1} +1) -9 + 1 = 9\cdot (3^{2n-1} +1) -8 | 9\cdot (3^{2n-1} +1) -9 + 1 = 9\cdot (3^{2n-1} +1) -8</math></center> | ||
</math></center> | |||
:Zarówno <math>(3^{2n+1} +1)</math> (na mocy założenia indukcyjnego) jak i '''8''' są podzielne przez '''4''', a więc ich różnica również. W ten sposób udowodniliśmy krok indukcyjny. | :Zarówno <math>(3^{2n+1} +1)</math> (na mocy założenia indukcyjnego) jak i '''8''' są podzielne przez '''4''', a więc ich różnica również. W ten sposób udowodniliśmy krok indukcyjny. | ||
| Linia 375: | Linia 347: | ||
* Jeśli hipoteza jest prawdą dla <math>n</math> i jeśli <math>n\geq 4</math> to | * Jeśli hipoteza jest prawdą dla <math>n</math> i jeśli <math>n\geq 4</math> to | ||
<center><math> | <center><math> | ||
(n+1)!= n!\cdot (n+1)>2^n\cdot(n+1)>2^{n+1} | (n+1)!= n!\cdot (n+1)>2^n\cdot(n+1)>2^{n+1}</math>,</center> | ||
</math></center> | |||
:gdzie pierwsza nierówność pochodzi z założenia indukcyjnego, a druga z faktu, że dowodzimy krok indukcyjny dla liczb większych niż '''4'''. | :gdzie pierwsza nierówność pochodzi z założenia indukcyjnego, a druga z faktu, że dowodzimy krok indukcyjny dla liczb większych niż '''4'''. | ||
| Linia 391: | Linia 362: | ||
:* Zakładamy teraz, że nierówność jest prawdziwa dla <math>n</math>, czyli że dla dowolnego <math>x</math> takiego, że <math>0\neq x> -1</math> mamy | :* Zakładamy teraz, że nierówność jest prawdziwa dla <math>n</math>, czyli że dla dowolnego <math>x</math> takiego, że <math>0\neq x> -1</math> mamy | ||
<center><math> | <center><math> | ||
{(1+x)}^n> 1+nx | {(1+x)}^n> 1+nx</math></center> | ||
</math></center> | |||
:Przekształcając nierówność dla <math>{n+1}</math> otrzymujemy | :Przekształcając nierówność dla <math>{n+1}</math> otrzymujemy | ||
::<math> | ::<math> | ||
{(1+x)}^{(n+1)}={(1+x)}^n(1+x)>(1+nx)(1+x)=1+(n+1)x +x^2\geq | {(1+x)}^{(n+1)}={(1+x)}^n(1+x)>(1+nx)(1+x)=1+(n+1)x +x^2\geq | ||
1+(n+1)x | 1+(n+1)x</math>, | ||
</math> | |||
:gdzie otrzymujemy ostrą nierówność dzięki założeniu indukcyjnemu i faktowi, że <math>x\neq -1</math>. W ten sposób krok indukcyjny został udowodniony. | :gdzie otrzymujemy ostrą nierówność dzięki założeniu indukcyjnemu i faktowi, że <math>x\neq -1</math>. W ten sposób krok indukcyjny został udowodniony. | ||
| Linia 410: | Linia 379: | ||
<u>'''Liczby Fibonacciego'''</u> zdefiniowane są następująco: | <u>'''Liczby Fibonacciego'''</u> zdefiniowane są następująco: | ||
<center><math> | <center><math> | ||
f_1=1, f_2=1 </math> oraz <math> | f_1=1, f_2=1</math> oraz <math>f_i=f_{i-2}+f_{i-1}</math> dla <math>i>3</math>.</center> | ||
Udowodnij, że dla dowolnego <math>n\geq 2</math> liczby <math>f_n</math> i <math>f_{n-1}</math> są względnie pierwsze. | Udowodnij, że dla dowolnego <math>n\geq 2</math> liczby <math>f_n</math> i <math>f_{n-1}</math> są względnie pierwsze. | ||
| Linia 437: | Linia 406: | ||
* Zakładamy, że hipoteza jest prawdziwa dla liczb od '''2''' do <math>n</math>. Weźmy liczbę <math>n+1</math>, jeśli <math>n+1</math> jest liczbą pierwszą, to hipoteza jest udowodniona. Jeśli <math>n+1</math> nie jest liczbą pierwszą, to <math>n+1=k\cdot l</math>, gdzie <math>2\leq k,l\leq n</math>. Założenie indukcyjne gwarantuje, że | * Zakładamy, że hipoteza jest prawdziwa dla liczb od '''2''' do <math>n</math>. Weźmy liczbę <math>n+1</math>, jeśli <math>n+1</math> jest liczbą pierwszą, to hipoteza jest udowodniona. Jeśli <math>n+1</math> nie jest liczbą pierwszą, to <math>n+1=k\cdot l</math>, gdzie <math>2\leq k,l\leq n</math>. Założenie indukcyjne gwarantuje, że | ||
<center><math> | <center><math> | ||
k=p_1\cdot p_2\cdot\dotsb\cdot p_i </math> i <math> l=q_1\cdot | k=p_1\cdot p_2\cdot\dotsb\cdot p_i</math> i <math>l=q_1\cdot | ||
q_2\cdot\dotsb\cdot q_j | q_2\cdot\dotsb\cdot q_j</math>,</center> | ||
</math></center> | |||
:gdzie <math>p_1,\dotsc,p_i,q_1,\dotsc,q_j</math> są liczbami pierwszymi. W związku z tym | :gdzie <math>p_1,\dotsc,p_i,q_1,\dotsc,q_j</math> są liczbami pierwszymi. W związku z tym | ||
<center><math> | <center><math> | ||
n+1=p_1\cdot p_2\cdot\dotsb\cdot p_i\cdot q_1\cdot | n+1=p_1\cdot p_2\cdot\dotsb\cdot p_i\cdot q_1\cdot | ||
q_2\cdot\dotsb\cdot q_j | q_2\cdot\dotsb\cdot q_j | ||
| Linia 464: | Linia 432: | ||
:* Zakładamy, że każda liczba mniejsza lub równa <math>n</math> może być przedstawiona w sposób opisany powyżej. Jeśli liczba <math>n+1</math> jest liczbą Fibonacciego, to krok indukcyjny jest już dowiedziony, jeśli nie, to znajdujemy największą liczbę Fibonacciego mniejszą od <math>n+1</math> - oznaczmy tę liczbę <math>f_k</math>. Liczba <math>n+1-f_k</math> jest mniejsza niż <math>n</math> więc, na mocy założenia indukcyjnego, posiada reprezentację jako suma liczb Fibonacciego | :* Zakładamy, że każda liczba mniejsza lub równa <math>n</math> może być przedstawiona w sposób opisany powyżej. Jeśli liczba <math>n+1</math> jest liczbą Fibonacciego, to krok indukcyjny jest już dowiedziony, jeśli nie, to znajdujemy największą liczbę Fibonacciego mniejszą od <math>n+1</math> - oznaczmy tę liczbę <math>f_k</math>. Liczba <math>n+1-f_k</math> jest mniejsza niż <math>n</math> więc, na mocy założenia indukcyjnego, posiada reprezentację jako suma liczb Fibonacciego | ||
<center><math> | <center><math> | ||
n+1-f_k=f_{l_0}+\dotsb+f_{l_i} | n+1-f_k=f_{l_0}+\dotsb+f_{l_i} | ||
</math></center> | </math></center> | ||
| Linia 470: | Linia 438: | ||
:tak, że każda z liczb w tej reprezentacji występuje co najwyżej raz. Oczywiście | :tak, że każda z liczb w tej reprezentacji występuje co najwyżej raz. Oczywiście | ||
<center><math> | <center><math> | ||
n+1 = f_k+f_{l_0}+\dotsb+f_{l_i} | n+1 = f_k+f_{l_0}+\dotsb+f_{l_i} | ||
</math></center> | </math></center> | ||
| Linia 505: | Linia 473: | ||
<center> | <center> | ||
<math> | <math> | ||
n^2\leq n_{xy}n_{xz}n_{yz} | n^2\leq n_{xy}n_{xz}n_{yz}</math> | ||
</math> | |||
</center> | </center> | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Podpowiedź 1</span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Podpowiedź 1</span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:Logika-2.2.svg|250x250px|thumb|right|opis obrazka]] | |||
Użyj nierówności pomiędzy średnią geometryczną a średnią arytmetyczną | Użyj nierówności pomiędzy średnią geometryczną a średnią arytmetyczną | ||
| Linia 520: | Linia 484: | ||
<center> | <center> | ||
<math> | <math> | ||
\frac{1}{2}(a+b)\geq \sqrt{ab} | \frac{1}{2}(a+b)\geq \sqrt{ab}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 541: | Linia 504: | ||
<center> | <center> | ||
<math> | <math> | ||
{n'}^2\leq n'_{xy}n'_{xz}n'_{yz} | {n'}^2\leq n'_{xy}n'_{xz}n'_{yz} | ||
</math> | </math> | ||
| Linia 551: | Linia 514: | ||
<center> | <center> | ||
<math> | <math> | ||
{n''}^2\leq n''_{xy}n''_{xz}n''_{yz} | {n''}^2\leq n''_{xy}n''_{xz}n''_{yz}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 561: | Linia 523: | ||
<center> | <center> | ||
<math> | <math> | ||
n'_{xz}+n''_{xz}=n_{xz} </math> oraz <math> | n'_{xz}+n''_{xz}=n_{xz}</math> oraz <math>n'_{yz}+n''_{yz}=n_{yz}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 571: | Linia 532: | ||
<center> | <center> | ||
<math> | <math> | ||
n'_{xy}\leq n_{xy} </math> oraz <math> | n'_{xy}\leq n_{xy}</math> oraz <math>n''_{xy}\leq n_{xy}</math> | ||
</math> | |||
</center> | </center> | ||
| Linia 580: | Linia 540: | ||
<center><math> | <center><math> | ||
\ | \begin{align} | ||
n^2& ={(n'+n'')}^2={(n')}^2+2n'n'' + {(n'')}^2\leq {(n')}^2+2\sqrt{{(n')}^2}\sqrt{{(n'')}^2} + {(n'')}^2\leq \\ | n^2& ={(n'+n'')}^2={(n')}^2+2n'n'' + {(n'')}^2\leq {(n')}^2+2\sqrt{{(n')}^2}\sqrt{{(n'')}^2} + {(n'')}^2\leq \\ | ||
& \leq n'_{xy}n'_{xz}n'_{yz} +2\sqrt{n'_{xy}n'_{xz}n'_{yz}}\sqrt{n''_{xy}n''_{xz}n''_{yz}}+n''_{xy}n''_{xz}n''_{yz} \leq\\ | & \leq n'_{xy}n'_{xz}n'_{yz} +2\sqrt{n'_{xy}n'_{xz}n'_{yz}}\sqrt{n''_{xy}n''_{xz}n''_{yz}}+n''_{xy}n''_{xz}n''_{yz} \leq\\ | ||
& \leq n_{xy}n'_{xz}n'_{yz} +2\sqrt{n_{xy}n'_{xz}n'_{yz}n_{xy}n''_{xz}n''_{yz}}+n_{xy}n''_{xz}n''_{yz} \leq \\ | & \leq n_{xy}n'_{xz}n'_{yz} +2\sqrt{n_{xy}n'_{xz}n'_{yz}n_{xy}n''_{xz}n''_{yz}}+n_{xy}n''_{xz}n''_{yz} \leq \\ | ||
& \leq n_{xy}\left(n'_{xz}n'_{yz} | & \leq n_{xy}\left(n'_{xz}n'_{yz} +2\sqrt{n'_{xz}n'_{yz}n''_{xz}n''_{yz}}+n''_{xz}n''_{yz}\right) | ||
+2\sqrt{n'_{xz}n'_{yz}n''_{xz}n''_{yz}}+n''_{xz}n''_{yz} | \end{align} | ||
\right)\ | |||
</math></center> | </math></center> | ||
| Linia 594: | Linia 553: | ||
<center><math> | <center><math> | ||
\ | \begin{align} | ||
n^2 & \leq n_{xy}\left(n'_{xz}n'_{yz} +2\sqrt{n'_{xz}n''_{xz}n'_{yz}n''_{yz}}+n''_{xz}n''_{yz}\right) \leq \\ | n^2 & \leq n_{xy}\left(n'_{xz}n'_{yz} +2\sqrt{n'_{xz}n''_{xz}n'_{yz}n''_{yz}}+n''_{xz}n''_{yz}\right) \leq \\ | ||
& \leq n_{xy}\left(n'_{xz}n'_{yz} +2\frac{1}{2}(n'_{xz}n''_{xz} +n'_{yz}n''_{yz})+n''_{xz}n''_{yz}\right) = \\ | & \leq n_{xy}\left(n'_{xz}n'_{yz} +2\frac{1}{2}(n'_{xz}n''_{xz} +n'_{yz}n''_{yz})+n''_{xz}n''_{yz}\right) = \\ | ||
& = n_{xy}\left(n'_{xz}n'_{yz} +n'_{xz}n''_{xz} | & = n_{xy}\left(n'_{xz}n'_{yz} +n'_{xz}n''_{xz}+n'_{yz}n''_{yz}+n''_{xz}n''_{yz}\right) = n_{xy}(n'_{xz} +n''_{xz})(n'_{yz}+n''_{yz}) | ||
+n'_{yz}n''_{yz}+n''_{xz}n''_{yz}\right) = n_{xy}(n'_{xz} + | \end{align} | ||
n''_{xz})(n'_{yz}+n''_{yz}) | |||
\ | |||
</math></center> | </math></center> | ||
| Linia 608: | Linia 565: | ||
<center><math> | <center><math> | ||
n^2\leq n_{xy}(n'_{xz} + n''_{xz})(n'_{yz}+n''_{yz})= | n^2\leq n_{xy}(n'_{xz} + n''_{xz})(n'_{yz}+n''_{yz})= | ||
n_{xy}n_{xz}n_{yz} | n_{xy}n_{xz}n_{yz}</math></center> | ||
</math></center> | |||
| Linia 647: | Linia 603: | ||
Załóżmy, że istnieje jedynie skończenie wiele liczb pierwszych <math>p_0,\dotsc,p_n</math>. Zdefiniujmy liczbę | Załóżmy, że istnieje jedynie skończenie wiele liczb pierwszych <math>p_0,\dotsc,p_n</math>. Zdefiniujmy liczbę | ||
<center><math> | <center><math> | ||
k = p_0\cdot p_1\cdot\dotsb\cdot p_n | k = p_0\cdot p_1\cdot\dotsb\cdot p_n | ||
</math></center> | </math></center> | ||
| Linia 659: | Linia 615: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Załóżmy, niewprost, że istnieje największa liczba naturalna i oznaczmy ją przez <math>\ | Załóżmy, niewprost, że istnieje największa liczba naturalna i oznaczmy ją przez <math>\text{n}</math>. Niewątpliwie <math>{n+1}</math> jest liczbą naturalną większą od <math>\text{n}</math>, co jest sprzecznością z naszym założeniem. | ||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 22:11, 11 wrz 2023
"Naiwna" teoria mnogości
Teoria zbiorów, zwana również teorią mnogości, została stworzona około połowy XIX wieku, przez niemieckiego matematyka Georga Cantora. Teoria mnogości to gałąź matematyki zajmująca się zbiorami - kolekcja obiektów. Skończone zbiory można definiować, wypisując kolejno wszystkie ich elementy. Georg Cantor był pierwszą osobą, która podjęła się przeniesienia na ścisły grunt matematyczny pojęcia zbioru nieskończonego. Według Georga Cantora zbiór może być dowolną kolekcją obiektów zwanych elementami. Według tego podejścia zbiór jest pojęciem podstawowym i niedefiniowalnym. Niestety podejście do teorii zbiorów w ten sposób rodzi paradoksy i dlatego teoria mnogości prezentowana w ten sposób jest często nazywana "naiwną" teorią mnogości.

Zobacz biografię
Teoria matematyczna nie może dopuszczać istnienia paradoksów i dlatego na początku XX wieku zmieniono podejście do teorii mnogości. Zaproponowany przez Ernsta Zermelo i uzupełniony przez Adolfa Abrahama Halevi Fraenkela system aksjomatów wyklucza paradoksy, które spowodowały, że naiwna teoria zbiorów musiała zostać porzucona. Aksjomaty te nakładają pewne ograniczenia na konstrukcje zaproponowane przez Georga Cantora. W większości przypadków jednak intuicje związane z naiwną teorią mnogości sprawdzają się również w aksjomatycznej teorii zbiorów. Zaprezentowane poniżej, skrótowe przedstawienie "naiwnej teorii mnogości" ma na celu wyrobienie intuicji niezbędnych przy dalszej pracy nad formalną wersją tych teorii. Aksjomatyczna teoria zbiorów zostanie przedstawiona w Wykładzie 4.
W podejściu zaproponowanym przez Georga Cantora zbiory skończone można łatwo wskazywać poprzez wyliczenie ich elementów. Definiowanie zbiorów nieskończonych wymaga bardziej rozwiniętego języka, niemniej jednak, według Georga Cantora, każda kolekcja obiektów jest zbiorem. Podstawowym symbolem używanym przy definiowaniu i opisywaniu zbiorów jest
oznaczający, że dany byt jest "elementem" pewnego zbioru. Napis
ilustruje zastosowanie tego symbolu.
Aby zdefiniować zbiór należy określić definitywny sposób na rozpoznawania, czy dany byt jest elementem zbioru, czy nie. Najczęściej używanym symbolem przy definiowaniu zbioru są nawiasy klamrowe. Definicja skończonego zbioru może być bardzo łatwa. Zbiór
posiada trzy elementy. Liczba 2 jest elementem tego zbioru
Kraków , ale również
Kraków , Kraków.
Dwa zbiory są sobie równe (takie same), jeśli posiadają dokładnie
te same elementy. Jedynymi elementami zbioru są liczby
naturalne 2 i 3 - ten sam fakt jest prawdziwy dla zbioru
, a więc
Podobnie i
4".
W definicji zbioru nie ma znaczenia kolejność, w jakiej wymienione są jego elementy, ani krotność w jakiej dany element pojawia się w zbiorze.

Zobacz biografię
Zbiory można definiować na wiele sposobów. Najprostszym sposobem zdefiniowania zbioru jest wyliczenie jego elementów. Strategia ta zawodzi jednak w odniesieniu do zbiorów nieskończonych -- nie jesteśmy w stanie wypisać wszystkich liczb naturalnych. Zgodnie z postulatami Georga Cantora możemy przyjąć, że istnieje zbiór wszystkich liczb naturalnych. Czasami, na określenie zbiorów nieskończonych używamy nieformalnego zapisu - zbiór wszystkich liczb naturalnych może być zapisany jako
W podejściu zaproponowanym przez Georga Cantora równoważna definicja tego zbioru brzmi
Bardzo często tworzymy zbiory składające się z obiektów spełniających daną własność. Zbiór liczb parzystych możemy zdefiniować w sposób następujący
Bardziej ogólnie
W skład powyżej zdefiniowanego zbioru wchodzą te elementy, które spełniają warunek występujący po znaku ,. Żeby zakwalifikować element do powyższego zbioru, wstawiamy go w miejsce w warunku występującym po , i sprawdzamy, czy jest on prawdziwy. Żeby pokazać, że
musimy dowieść, że warunek "2 jest liczbą parzystą" jest prawdziwy.
Pomiędzy zbiorem liczb parzystych a zbiorem wszystkich liczb naturalnych występuje oczywista zależność. Każda liczba parzysta jest liczbą naturalną, co, ujęte w języku zbiorów, oznacza, że każdy element zbioru liczb parzystych jest elementem zbioru liczb naturalnych. Zbiór liczb parzystych jest podzbiorem zbioru liczb naturalnych (a zbiór liczb naturalnych nadzbiorem zbioru liczb parzystych). Zapisujemy to w następujący sposób
Ogólniej, jeśli każdy element zbioru jest elementem zbioru mówimy, że zbiór jest podzbiorem zbioru i piszemy
W takim przypadku mówimy, że pomiędzy zbiorami i zachodzi inkluzja.
W szczególności, dla dowolnego zbioru zachodzi . Wspomnieliśmy wcześniej, że dwa zbiory są sobie równe wtedy i tylko wtedy, kiedy posiadają dokładnie takie same elementy. Fakt ten możemy zapisać formalnie w następujący sposób
Często zależy nam na określeniu znaczącym, że jeden zbiór jest podzbiorem drugiego i że zbiory te nie są sobie równe. Używamy wtedy symbolu w następujący sposób
Ćwiczenie 1.1
Dla każdej pary zbiorów poniżej określ, czy są sobie równe oraz czy jeden z nich jest nadzbiorem drugiego
- , dzieli liczbę ,
- "zbiór liczb naturalnych" , dzieli ,
- , .
Najczęstszymi operacjami wykonywanymi na zbiorach są operacje
sumy, przecięcia i różnicy. Sumą dwóch
zbiorów i jest zbiór oznaczony przez w skład
którego wchodzą wszystkie elementy zbioru , wszystkie elementy
zbioru i żadne elementy spoza tych zbiorów

Podobnie definiujemy przecięcie zbiorów

Ćwiczenie 1.2
Dla następujących par zbiorów ustal zawieranie lub równość
- "zbiór liczb naturalnych" liczba nieparzysta, większa niż 2 dzieli
i drugi zbiór gdzie jest liczbą naturalną , - liczba 2 dzieli liczba 3 dzieli i zbiór liczba 6 dzieli .
Dla dowolnego zbioru zachodzi i . Zbiór, który otrzymujemy jako wynik operacji jest zbiorem pustym. Na mocy definicji różnicy zbiorów elementami zbioru są wyłącznie te elementy , które nie należą do . Takie elementy nie istnieją - żaden element ze zbioru nie należy do i żaden element spoza nie należy do tego zbioru. Zbiór pusty jest oznaczany przez . Odejmowanie zbiorów od samych siebie nie jest jedynym sposobem na otrzymanie zbioru pustego.
Zbiór po lewej stronie nierówności jest równy zbiorowi po prawej stronie nierówności. Każdy element zbioru po prawej stronie jest również elementem zbioru po lewej stronie nierówności i vice versa, dlatego że żaden z tych zbiorów nie posiada elementów.

Zobacz biografię
Niestety, podejście zaproponowane przez Georga Cantora i uściślone przez Friedricha Frege posiada błędy. Jedną z pierwszych osób które zwróciły uwagę na niedociągnięcia tej teorii jest Bertrand Russell. Zgodnie z zasadami zaproponowanymi przez [Biografia_Cantor|Georga Cantora]] można zdefiniować dowolny zbiór. Zdefiniujmy, więc zbiór
Zbiór składa się ze zbiorów, które nie są swoimi własnymi elementami. Paradoks zaproponowany przez Bertranda Russella polega na tym, że pytanie czy jest swoim własnym elementem prowadzi do sprzeczności. Jeśli to, zgodnie z definicją zbioru otrzymujemy , co jest sprzecznością z założeniem. Jeśli , to spełnia warunek na przynależność do i w związku z tym , co jest kolejną sprzecznością. Definicja zbioru zaproponowana przez Georga Cantora prowadzi do powstania logicznych paradoksów. Okazuje się, że pytanie: co jest zbiorem, jest trudniejsze niż wydawało się matematykom końca XIX wieku.
W dalszej części wykładu przedstawimy właściwe podejście do teorii mnogości. Podejście to jest oparte o część logiki zwaną rachunkiem predykatów. Podejście to zostało zaproponowane przez Ernsta Zermelo na początku XX wieku i ma na celu dostarczenie spójnej teorii zbiorów o mocy podobnej do naiwnej teorii, przy równoczesnym uniknięciu paradoksów. Aksjomatyczna teoria mocy definiuje bardzo dokładnie, które kolekcje obiektów są zbiorami. W szczególności paradoks zaproponowany przez Bertranda Russella nie pojawia się w aksjomatycznej teorii zbiorów, ponieważ zbiór zdefiniowany powyżej jako w niej nie istnieje.
"Naiwna" indukcja

Zobacz biografię
Zasada indukcji matematycznej jest o prawie trzysta lat starsza niż teoria mnogości. Pierwszy dowód indukcyjny pojawił się w pracy
Francesco Maurolico w 1575 roku. W pracy tej autor wykazał, że suma pierwszych liczb nieparzystych równa się .
Aby zastosować zasadę indukcji matematycznej, należy wykazać dwa fakty:
- hipoteza jest prawdziwa dla ,
- jeśli hipoteza jest prawdziwa dla , to jest również prawdziwa dla .
Drugi z powyższych punktów musi być prawdą dla wszystkich . Jeśli oba fakty są prawdą, to hipoteza jest prawdziwa dla wszystkich liczb naturalnych większych od 1. Rozumowanie, które stoi za tym wnioskiem wygląda następująco:
- hipoteza jest prawdziwa dla na podstawie podstawy indukcji,
- hipoteza jest prawdziwa dla , ponieważ jest prawdziwa dla 1 i po zastosowaniu kroku indukcyjnego również dla 2,
- hipoteza jest prawdziwa dla ; w poprzednim punkcie pokazaliśmy, że jest prawdziwa dla 2 i na podstawie kroku indukcyjnego jest również prawdziwa 3,
- i tak dalej.

Zasadę indukcji matematycznej można porównać do domina. Aby mieć pewność, że przewrócone zostaną wszystkie klocki wystarczy wykazać, że przewrócony zostanie pierwszy klocek i że każdy klocek pociąga za sobą następny.
Dowód indukcyjny przedstawiony przez Francesco Maurolico pokazuje, że suma pierwszych liczb nieparzystych jest równa .
- Jeśli to pierwsza liczba nieparzysta 1 jest równa .
- Jeśli hipoteza jest prawdą dla , to znaczy że suma pierwszych liczb nieparzystych równa się . Bardziej formalnie
tak więc suma pierwszych liczb nieparzystych , przy użyciu założenia powyżej może być zapisana jako
Krok indukcyjny został dowiedziony.
Ćwiczenie 2.1
Wykaż, że suma pierwszych liczb naturalnych jest równa .
Ćwiczenie 2.2
Wykaż, że suma kwadratów pierwszych liczb naturalnych jest równa .
Ćwiczenie 2.3
Wykaż, że dla zachodzi .
Często bardzo niepraktyczne jest używanie indukcji w jej podstawowej formie. Używa się wtedy indukcji, która w pierwszym kroku nie zaczyna się od , ale , lub dowolnej innej liczby naturalnej. W takim przypadku drugi krok indukcyjny nie musi działać dla wszystkich , a wystarczy, by działał dla większych lub równych od liczby, którą wybraliśmy w pierwszym kroku. Końcowy dowód indukcyjny pokaże, że dana hipoteza nie jest prawdziwa dla wszystkich liczb naturalnych, a jedynie dla liczb większych od tej wybranej na pierwszy krok indukcyjny.
Jako przykład pokażemy, że . Po pierwsze nierówność ta nie zachodzi dla , więc nie można rozpocząć kroku indukcyjnego od . Indukcja będzie wyglądać następująco:
- Hipoteza jest prawdą dla , ponieważ .
- Jeśli hipoteza jest prawdą dla i jeśli to
- gdzie pierwsza nierówność pochodzi z założenia indukcyjnego, a druga z faktu, że dowodzimy krok indukcyjny dla liczb większych niż 4.
Ćwiczenie 2.4
W tym ćwiczeniu dowodzimy wariant nierówności Bernoulliego. Dla dowolnego takiego, że i i dla dowolnego zachodzi .
Ćwiczenie 2.5
Liczby Fibonacciego zdefiniowane są następująco:
Udowodnij, że dla dowolnego liczby i są względnie pierwsze.
Kolejnym uogólnieniem zasady indukcji matematycznej jest indukcja, w której w drugim kroku indukcyjnym zakładamy, że hipoteza jest prawdą dla wszystkich liczb mniejszych niż i dowodzimy, że jest również prawdziwa dla .
Jako przykład udowodnimy, że każda liczba naturalna większa niż 2 jest produktem jednej, lub więcej liczb pierwszych.
- Hipoteza jest prawdą dla , ponieważ 2 jest liczbą pierwszą.
- Zakładamy, że hipoteza jest prawdziwa dla liczb od 2 do . Weźmy liczbę , jeśli jest liczbą pierwszą, to hipoteza jest udowodniona. Jeśli nie jest liczbą pierwszą, to , gdzie . Założenie indukcyjne gwarantuje, że
- gdzie są liczbami pierwszymi. W związku z tym
- i krok indukcyjny jest udowodniony.
Ćwiczenie 2.6
Udowodnij, że każda liczba naturalna większa niż 1 może być przedstawiona jako suma liczb Fibonacciego tak, że żadna liczba nie występuje w tej sumie więcej niż raz.
Ćwiczenie 2.7
Znajdź błąd w poniższym dowodzie indukcyjnym. Dowodzimy indukcyjnie twierdzenia, że wszystkie liczby są parzyste.
- Twierdzenie jest prawdą dla ponieważ 0 jest liczbą parzystą.
- Zakładamy, że twierdzenie jest prawdą dla wszystkich liczb mniejszych lub równych . Liczba jest niewątpliwie sumą dwóch liczb silnie mniejszych od siebie . Liczby i , na podstawie założenia indukcyjnego, są parzyste, zatem ich suma równa jest parzysta. Krok indukcyjny został dowiedziony.
Na zasadzie indukcji matematycznej wszystkie liczby są parzyste.
Ćwiczenie 2.8
W trójwymiarowej przestrzeni znajduje się punktów. Ilość punktów w rzutowaniu na płaszczyznę oznaczamy przez . Podobnie ilość punktów w rzutowaniu na przez i ilość punktów w rzutowaniu na przez . Wykaż, że dla dowolnego rozkładu punktów w przestrzeni zachodzi nierówność
Zasada indukcji matematycznej jest bardzo potężnym narzędziem. Intuicyjnie wydaje się jasne, że dowody przeprowadzone przy jej pomocy są poprawne. Niemniej jednak, żeby uzasadnić poprawność samej zasady, należy sięgnąć do teorii mnogości i definicji zbioru liczb naturalnych. Wiemy już, że "naiwna teoria mnogości" nie daje nam poprawnych zbiorów, na których można oprzeć ścisłe rozumowanie. W dalszej części wykładu wyprowadzimy zasadę indukcji matematycznej w oparciu o aksjomaty i aksjomatycznie zdefiniowany zbiór liczb naturalnych. Takie podejście gwarantuje nam poprawność rozumowania -- podejście naiwne zapewnia intuicje niezbędne do budowania poprawnych teorii.
"Naiwne" dowody niewprost

Zobacz biografię
Częstą metodą dowodzenia twierdzeń matematycznych jest dowodzenie niewprost. Dowód niewprost polega na założeniu zaprzeczenia twierdzenia, które chcemy udowodnić i doprowadzeniu do sprzeczności. Wykazujemy, że jeśli twierdzenie nasze jest nieprawdziwe, jesteśmy w stanie udowodnić jakąś tezę, która jest w sposób oczywisty fałszywa.
Jednym z najbardziej znanych dowodów niewprost jest dowód istnienia nieskończenie wielu liczb pierwszych. Dowód ten został zaproponowany przez Euklidesa z Aleksandrii, a my prezentujemy go w wersji podanej przez Ernsta Kummera.
Twierdzenie 3.1
Istnieje nieskończenie wiele liczb pierwszych.
Dowód
Załóżmy, że istnieje jedynie skończenie wiele liczb pierwszych . Zdefiniujmy liczbę
i rozważmy . Liczba posiada dzielnik pierwszy, a ponieważ jedynymi pierwszymi liczbami są liczby , wnioskujemy, że dzieli dla pewnego . Liczba dzieli również , a więc dzieli co jest sprzecznością.
Ćwiczenie 3.1
Wykaż, że nie istnieje największa liczba naturalna.
Ćwiczenie 3.2
Wykaż, że jest liczbą niewymierną.
Ścisłe uzasadnienie poprawności dowodów niewprost leży na gruncie logiki, której poświęcony jest następny wykład.