Analiza matematyczna 2/Ćwiczenia 2: Ciągi w przestrzeniach metrycznych: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
||
| (Nie pokazano 18 wersji utworzonych przez 3 użytkowników) | |||
| Linia 3: | Linia 3: | ||
{{cwiczenie|2.1.|cw_2_1| | {{cwiczenie|2.1.|cw_2_1| | ||
Niech <math> | Niech <math>(X,d)</math> będzie przestrzenią metryczną, niech | ||
<math> | <math>\{x_n\}\subseteq X</math> będzie ciągiem oraz niech <math>g\in X</math>. | ||
Udowodnić, że | Udowodnić, że | ||
jeśli <math> | jeśli <math>\lim\limits_{n\rightarrow +\infty} x_n=g</math> oraz | ||
<math> | <math>\big\{x_{n_k}\big\}</math> jest dowolnym podciągiem ciągu | ||
<math> | <math>\{x_n\}</math>, to | ||
<center><math> | <center><math>\lim\limits_{k\rightarrow +\infty} x_{n_k} | ||
= | |||
g | g | ||
</math></center> | </math></center> | ||
| Linia 18: | Linia 18: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Należy zauważyć, że zachodzenie danej własności dla | |||
od pewnego miejsca dla ciągu implikuje zachodzenie tej własności | od pewnego miejsca dla ciągu implikuje zachodzenie tej własności | ||
od pewnego miejsca dla podciągu. | od pewnego miejsca dla podciągu. | ||
| Linia 24: | Linia 24: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>\lim\limits_{n\rightarrow +\infty} x_n=g</math> | ||
Należy pokazać, że <math> | Należy pokazać, że <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g</math> | ||
Weźmy dowolne <math> | Weźmy dowolne <math>\varepsilon>0</math> | ||
Z definicji granicy wiemy, że wszystkie | Z definicji granicy wiemy, że wszystkie | ||
wyrazy ciągu <math> | wyrazy ciągu <math>\{x_n\}</math> | ||
od pewnego miejsca leżą w kuli <math> | od pewnego miejsca leżą w kuli <math>K(g,\varepsilon)</math> | ||
Ale to oznacza, że także | Ale to oznacza, że także | ||
wszystkie wyrazy podciągu <math> | wszystkie wyrazy podciągu <math>\{x_{n_k}\}</math> od pewnego miejsca leżą w | ||
kuli <math> | kuli <math>K(g,\varepsilon)</math> | ||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, | ||
zatem z definicji granicy | zatem z definicji granicy | ||
wnioskujemy, że <math> | wnioskujemy, że <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g</math> | ||
</div></div> | </div></div> | ||
{{cwiczenie|2.2.|cw_2_2| | {{cwiczenie|2.2.|cw_2_2| | ||
Niech <math> | Niech <math>(X,d)</math> będzie przestrzenią metryczną, | ||
<math> | <math>\{x_n\}\subseteq X</math> ciągiem oraz niech <math>g\in X</math> | ||
Udowodnić, że | Udowodnić, że | ||
jeśli <math> | jeśli <math>\{x_n\}</math> jest ciągiem zbieżnym oraz | ||
<math> | <math>\big\{x_{n_k}\big\}</math> jest jego dowolnym podciągiem takim, | ||
że | że | ||
<math> | <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g</math> | ||
to także <math> | to także <math>\lim\limits_{n\rightarrow +\infty} x_n=g</math> | ||
}} | }} | ||
| Linia 56: | Linia 56: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Z założenia wiemy, że <math> | Z założenia wiemy, że <math>\lim\limits_{n\rightarrow +\infty} x_n=g_1</math> | ||
Z punktu (1) wynika, że także dla podciągu <math> | Z punktu (1) wynika, że także dla podciągu <math>\{x_{n_k}\}</math> | ||
mamy <math> | mamy <math>\lim\limits_{k\rightarrow +\infty} x_{n_k}=g_1</math> | ||
Z jedyności granicy | Z jedyności granicy | ||
(patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_6|twierdzenie 2.6.]]) mamy, że | (patrz [[Analiza matematyczna 2/Wykład 2: Ciągi w przestrzeniach metrycznych#tw_2_6|twierdzenie 2.6.]]) mamy, że | ||
<math> | <math>g=g_1</math>, co należało dowieść. | ||
</div></div> | </div></div> | ||
<span id="cw_2_3">{{cwiczenie|2.3.|| | <span id="cw_2_3">{{cwiczenie|2.3.|| | ||
Niech <math> | Niech <math>(X_i,d_i)</math> będą przestrzeniami metrycznymi dla <math>i=1,\ldots k,X=X_1\times\ldots\times X_k,\{a_n\}\subseteq X</math> ciągiem w <math>X</math> | ||
(w | (w | ||
szczególności | szczególności | ||
<math> | <math>a_n=(a_n^1,\ldots,a_n^k)</math> dla <math>n\in\mathbb{N}</math> | ||
oraz <math> | oraz <math>a=(a^1,\ldots,a^k)\in X</math>). | ||
Udowodnić, że:<br> | Udowodnić, że:<br> | ||
'''(1)''' | '''(1)''' | ||
<math> | <math>\lim\limits_{n\rightarrow +\infty} a_n=a</math>, | ||
wtedy i tylko wtedy, gdy | wtedy i tylko wtedy, gdy | ||
<math> | <math>\lim\limits_{n\rightarrow +\infty} a_n^i= a^i</math> | ||
dla <math> | dla <math>i=1,\ldots,k</math>.<br> | ||
<br> | <br> | ||
'''(2)''' Ciąg | '''(2)''' Ciąg | ||
<math> | <math>\{a_n\}</math> spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy | ||
ciągi <math> | ciągi <math>\{a^i_n\}</math> spełniają warunek Cauchy'ego dla <math>i=1,\ldots,k</math> | ||
}}<span> | }}<span> | ||
| Linia 94: | Linia 94: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' | '''(1)''' | ||
"<math> | "<math>\Longrightarrow</math>":<br> | ||
Załóżmy, że <math> | Załóżmy, że <math>\lim\limits_{n\rightarrow +\infty} a_n=a</math> | ||
Ustalmy <math> | Ustalmy <math>i_0\in\{1,\ldots,k\}</math>. | ||
Należy pokazać, że <math> | Należy pokazać, że <math>\lim\limits_{n\rightarrow +\infty} a_n^{i_0}= a^{i_0}</math> | ||
Ustalmy dowolne <math> | Ustalmy dowolne <math>\varepsilon>0</math> | ||
Z definicji granicy ciągu wiemy, że | Z definicji granicy ciągu wiemy, że | ||
<center><math> | <center><math>\exists N\in\mathbb{N}\ \forall n\ge N: | ||
d(a_n,a)<\varepsilon | d(a_n,a)<\varepsilon</math>,</center> | ||
</math></center> | |||
gdzie | gdzie | ||
<center><math> | <center><math>d(a_n,a) | ||
= | |||
\sqrt{d_1(a_n^1,a^1)^2+\ldots+d_k(a_n^k,a^k)^2} | \sqrt{d_1(a_n^1,a^1)^2+\ldots+d_k(a_n^k,a^k)^2} | ||
</math></center> | </math></center> | ||
Zatem dla <math> | Zatem dla <math>n\ge N</math> mamy | ||
<center><math> | <center><math>d_{i_0}(a_n^{i_0},a^{i_0}) | ||
\le | |||
\sqrt{d_1(a_n^1,a^1)^2+\ldots+d_k(a_n^k,a^k)^2} | \sqrt{d_1(a_n^1,a^1)^2+\ldots+d_k(a_n^k,a^k)^2} | ||
= | |||
d(a_n,a) | d(a_n,a) | ||
< | |||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
<center><math> | <center><math>\forall\varepsilon>0 | ||
\exists N\in\mathbb{N}\ \forall n\ge N: | \exists N\in\mathbb{N}\ \forall n\ge N: | ||
d_{i_0}(a_n^{i_0},a^{i_0})<\varepsilon | d_{i_0}(a_n^{i_0},a^{i_0})<\varepsilon | ||
</math></center> | </math></center> | ||
co oznacza, że <math> | co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n^{i_0}= a^{i_0}</math><br> | ||
"<math> | "<math>\Longleftarrow</math>":<br> | ||
Załóżmy, że <math> | Załóżmy, że <math>\lim\limits_{n\rightarrow +\infty} a_n^i= a^i</math> dla każdego | ||
<math> | <math>i\in\{1,\ldots,k\}</math>. | ||
Należy pokazać, że <math> | Należy pokazać, że <math>\lim\limits_{n\rightarrow +\infty} a_n=a</math> | ||
W tym celu ustalmy dowolne <math> | W tym celu ustalmy dowolne <math>\varepsilon>0</math>. | ||
Z definicji granicy ciągu wynika, że | Z definicji granicy ciągu wynika, że | ||
<center><math> | <center><math>\forall i\in\{1,\ldots,k\} | ||
\exists N_i\in\mathbb{N}\ \forall n\ge N_i: | \exists N_i\in\mathbb{N}\ \forall n\ge N_i: | ||
d_i(a_n^i,a^i)<\frac{\varepsilon}{\sqrt{k}} | d_i(a_n^i,a^i)<\frac{\varepsilon}{\sqrt{k}} | ||
</math></center> | </math></center> | ||
Niech <math> | Niech <math>N=\max\{N_1,\ldots,N_k\}</math> | ||
Wówczas dla <math> | Wówczas dla <math>n\ge N</math> mamy | ||
<center><math> | <center><math>d(a_n,a) | ||
= | |||
\sqrt{d_1(a_n^1,a^1)^2+\ldots+d_k(a_n^k,a^k)^2} | \sqrt{d_1(a_n^1,a^1)^2+\ldots+d_k(a_n^k,a^k)^2} | ||
< | |||
\sqrt{k\cdot \frac{\varepsilon^2}{k}} | \sqrt{k\cdot \frac{\varepsilon^2}{k}} | ||
= | |||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
<center><math> | <center><math>\forall\varepsilon>0 | ||
\exists N\in\mathbb{N}\ \forall n\ge N: | \exists N\in\mathbb{N}\ \forall n\ge N: | ||
d(a_n,a)<\varepsilon | d(a_n,a)<\varepsilon</math>,</center> | ||
</math></center> | |||
co oznacza, że <math> | co oznacza, że <math>\lim\limits_{n\rightarrow +\infty} a_n= a</math><br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
"<math> | "<math>\Longrightarrow</math>":<br> | ||
Załóżmy, że ciąg <math> | Załóżmy, że ciąg <math>\{a_n\}</math> spełnia warunek Cauchy'ego. | ||
Ustalmy <math> | Ustalmy <math>i_0\in\{1,\ldots,k\}</math> | ||
Należy pokazać, że ciąg <math> | Należy pokazać, że ciąg <math>\{a_n^{i_0}\}</math> | ||
spełnia warunek Cauchy'ego. | spełnia warunek Cauchy'ego. | ||
Ustalmy dowolne <math> | Ustalmy dowolne <math>\varepsilon>0</math> | ||
Z definicji warunku Cauchy'ego wiemy, że | Z definicji warunku Cauchy'ego wiemy, że | ||
<center><math> | <center><math>\exists N\in\mathbb{N}\ \forall n,m\ge N: | ||
d(a_n,a_m)<\varepsilon | d(a_n,a_m)<\varepsilon | ||
</math></center> | </math></center> | ||
gdzie | gdzie | ||
<center><math> | <center><math>d(a_n,a_m) | ||
= | |||
\sqrt{d_1(a_n^1,a_m^1)^2+\ldots+d_k(a_n^k,a_m^k)^2} | \sqrt{d_1(a_n^1,a_m^1)^2+\ldots+d_k(a_n^k,a_m^k)^2} | ||
</math></center> | </math></center> | ||
Zatem dla <math> | Zatem dla <math>n,m\ge N</math> mamy | ||
<center><math> | <center><math>d_{i_0}(a_n^{i_0},a_m^{i_0}) | ||
\le | |||
\sqrt{d_1(a_n^1,a_m^1)^2+\ldots+d_k(a_n^k,a_m^k)^2} | \sqrt{d_1(a_n^1,a_m^1)^2+\ldots+d_k(a_n^k,a_m^k)^2} | ||
= | |||
d(a_n,a_m) | d(a_n,a_m) | ||
< | |||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
<center><math> | <center><math>\forall\varepsilon>0 | ||
\exists N\in\mathbb{N}\ \forall n,m\ge N: | \exists N\in\mathbb{N}\ \forall n,m\ge N: | ||
d_{i_0}(a_n^{i_0},a_m^{i_0})<\varepsilon | d_{i_0}(a_n^{i_0},a_m^{i_0})<\varepsilon | ||
</math></center> | </math></center> | ||
co oznacza, że ciąg <math> | co oznacza, że ciąg <math>\{a_n^{i_0}\}</math> | ||
spełnia warunek Cauchy'ego.<br> | spełnia warunek Cauchy'ego.<br> | ||
<br> | <br> | ||
"<math> | "<math>\Longleftarrow</math>":<br> | ||
Załóżmy, że ciąg <math> | Załóżmy, że ciąg <math>\{a_n^i\}</math> spełnia warunek Cauchy'ego dla każdego | ||
<math> | <math>i\in\{1,\ldots,k\}</math>. | ||
Należy pokazać, że ciąg <math> | Należy pokazać, że ciąg <math>\{a_n\}</math> | ||
spełnia warunek Cauchy'ego. | spełnia warunek Cauchy'ego. | ||
W tym celu ustalmy dowolne <math> | W tym celu ustalmy dowolne <math>\varepsilon>0</math> | ||
Z definicji warunku Cauchy'ego wynika, że | Z definicji warunku Cauchy'ego wynika, że | ||
<center><math> | <center><math>\forall i\in\{1,\ldots,k\} | ||
\exists N_i\in\mathbb{N}\ \forall n,m\ge N_i: | \exists N_i\in\mathbb{N}\ \forall n,m\ge N_i: | ||
d_i(a_n^i,a_m^i)<\frac{\varepsilon}{\sqrt{k}} | d_i(a_n^i,a_m^i)<\frac{\varepsilon}{\sqrt{k}} | ||
</math></center> | </math></center> | ||
Niech <math> | Niech <math>N=\max\{N_1,\ldots,N_k\}</math> | ||
Wówczas dla <math> | Wówczas dla <math>n,m\ge N</math> mamy | ||
<center><math> | <center><math>d(a_n,a_m) | ||
= | |||
\sqrt{d_1(a_n^1,a_m^1)^2+\ldots+d_k(a_n^k,a_m^k)^2} | \sqrt{d_1(a_n^1,a_m^1)^2+\ldots+d_k(a_n^k,a_m^k)^2} | ||
< | |||
\sqrt{k\cdot \frac{\varepsilon^2}{k}} | \sqrt{k\cdot \frac{\varepsilon^2}{k}} | ||
= | |||
\varepsilon | \varepsilon</math></center> | ||
</math></center> | |||
Ponieważ <math> | Ponieważ <math>\varepsilon>0</math> było dowolnie wybrane, więc pokazaliśmy, że | ||
<center><math> | <center><math>\forall\varepsilon>0 | ||
\exists N\in\mathbb{N}\ \forall n,m\ge N: | \exists N\in\mathbb{N}\ \forall n,m\ge N: | ||
d(a_n,a_m)<\varepsilon | d(a_n,a_m)<\varepsilon | ||
</math></center> | </math></center> | ||
co oznacza, że ciąg <math> | co oznacza, że ciąg <math>\{a_n\}</math> | ||
spełnia warunek Cauchy'ego. | spełnia warunek Cauchy'ego. | ||
</div></div> | </div></div> | ||
| Linia 243: | Linia 237: | ||
{{cwiczenie|2.4.|cw_2_4| | {{cwiczenie|2.4.|cw_2_4| | ||
Pokazać z definicji, że <math> | Pokazać z definicji, że <math>\mathbb{R}^2</math> (z metryką euklidesową) nie jest zbiorem | ||
zwartym. | zwartym. | ||
}} | }} | ||
| Linia 253: | Linia 247: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważmy rodzinę zbiorów otwartych | Rozważmy rodzinę zbiorów otwartych | ||
<math> | <math>\big\{K\big((0,0),n\big)\big\}_{n\in\mathbb{N}}</math> | ||
Ponieważ | Ponieważ | ||
<center><math> | <center><math>\mathbb{R}^2 | ||
= | |||
\bigcup_{n\in\mathbb{N}} K\big((0,0),n\big) | \bigcup_{n\in\mathbb{N}} K\big((0,0),n\big) | ||
</math></center> | </math></center> | ||
zatem rodzina ta jest pokryciem zbioru <math> | zatem rodzina ta jest pokryciem zbioru <math>\mathbb{R}^2</math> | ||
Pokażemy, że z tego pokrycia nie można wybrać podpokrycia | Pokażemy, że z tego pokrycia nie można wybrać podpokrycia | ||
skończonego. Dla dowodu niewprost przypuśćmy, że istnieje | skończonego. Dla dowodu niewprost przypuśćmy, że istnieje | ||
podpokrycie skończone | podpokrycie skończone | ||
<math> | <math>\big\{K\big((0,0),n_i\big)\big\}_{i=1}^k</math> | ||
Zdefiniujmy <math> | Zdefiniujmy <math>n_0=\max\{n_1,\ldots, n_k\}</math> | ||
Wówczas | Wówczas | ||
<center><math> | <center><math>\bigcup_{i=1}^k K\big((0,0),n_i\big) | ||
= | |||
K\big((0,0),n_0\big) | K\big((0,0),n_0\big) | ||
\subsetneq \mathbb{R}^2 | \subsetneq \mathbb{R}^2 | ||
| Linia 276: | Linia 270: | ||
(ostatnie istotne zawieranie wynika na przykład z faktu, | (ostatnie istotne zawieranie wynika na przykład z faktu, | ||
że punkt <math> | że punkt <math>(0,n_0+1)\in\mathbb{R}^2\setminus K\big((0,0),n_0\big)</math>) | ||
Otrzymaliśmy sprzeczność. | Otrzymaliśmy sprzeczność. | ||
Zatem zbiór <math> | Zatem zbiór <math>\mathbb{R}^2</math> nie jest zwarty. | ||
</div></div> | </div></div> | ||
| Linia 299: | Linia 293: | ||
zbiór jest zwarty wtedy i tylko wtedy, gdy | zbiór jest zwarty wtedy i tylko wtedy, gdy | ||
jest skończony.<br> | jest skończony.<br> | ||
"<math> | "<math>\Longleftarrow</math>"<br> | ||
Jeśli <math> | Jeśli <math>A</math> jest zbiorem skończonym, to jest zwarty | ||
(w dowolnej przestrzeni metrycznej; | (w dowolnej przestrzeni metrycznej; | ||
patrz [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_19|twierdzenia 1.19.]] (1)).<br> | patrz [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_19|twierdzenia 1.19.]] (1)).<br> | ||
"<math> | "<math>\Longrightarrow</math>"<br> | ||
Niech <math> | Niech <math>A</math> będzie zbiorem zwartym w przestrzeni metrycznej | ||
dyskretnej. | dyskretnej. | ||
Należy pokazać, że zbiór <math> | Należy pokazać, że zbiór <math>A</math> jest skończony. | ||
Dla dowodu niewprost przypuśćmy, że | Dla dowodu niewprost przypuśćmy, że | ||
zbiór <math> | zbiór <math>A</math> jest nieskończony. | ||
Rozważmy następującą rodzinę zbiorów otwartych | Rozważmy następującą rodzinę zbiorów otwartych | ||
<math> | <math>\{K(x,1)\}_{x\in A}</math>. | ||
Ponieważ <math> | Ponieważ <math>K(x,1)=\{x\}</math> zatem rodzina ta jest pokryciem | ||
otwartym (i nieskończonym) zbioru | otwartym (i nieskończonym) zbioru | ||
<math> | <math>A</math> zbiorami jednopunktowymi. Zauważmy, że po usunięciu z tej | ||
rodziny dowolnego zbioru, przestaje ona być pokryciem zbioru | rodziny dowolnego zbioru, przestaje ona być pokryciem zbioru | ||
<math> | <math>A</math>. Zatem nie można z niego wybrać podpokrycia skończonego. | ||
Zatem zbiór <math> | Zatem zbiór <math>A</math> nie jest zwarty i otrzymujemy sprzeczność. | ||
</div></div> | </div></div> | ||
{{cwiczenie|2.6.|cw_2_6| | {{cwiczenie|2.6.|cw_2_6| | ||
Niech <math> | Niech <math>X</math> będzie przestrzenią metryczną | ||
oraz <math> | oraz <math>A,B\subseteq X</math>. Które z implikacji są prawdziwe:<br> | ||
"jeśli zbiory <math> | "jeśli zbiory <math>A</math> i <math>B</math> są spójne, to zbiór <math>A\cap B</math> jest | ||
spójny";<br> | spójny";<br> | ||
"jeśli zbiory <math> | "jeśli zbiory <math>A</math> i <math>B</math> są spójne, to zbiór <math>A\cup B</math> jest | ||
spójny";<br> | spójny";<br> | ||
"jeśli zbiór <math> | "jeśli zbiór <math>A\cup B</math> jest spójny, to zbiory <math>A</math> i <math>B</math> są | ||
spójne". | spójne". | ||
}} | }} | ||
| Linia 333: | Linia 327: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Ewentualnych kontrprzykładów można szukać w | Ewentualnych kontrprzykładów można szukać w | ||
<math> | <math>\mathbb{R}^2</math>. | ||
</div></div> | </div></div> | ||
| Linia 340: | Linia 334: | ||
Przecięcie zbiorów spójnych nie musi być zbiorem | Przecięcie zbiorów spójnych nie musi być zbiorem | ||
spójnym. | spójnym. | ||
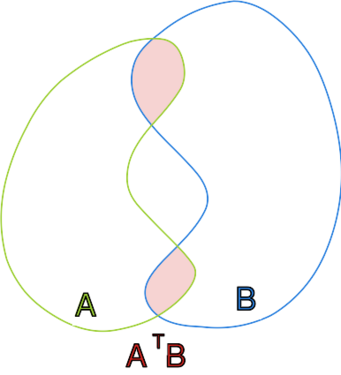
Rysunek przedstawia dwa zbiory spójne <math> | Rysunek przedstawia dwa zbiory spójne <math>A,B\subseteq \mathbb{R}^2</math>, | ||
których przecięcie <math> | których przecięcie <math>A\cap B</math> nie jest spójne.<br> | ||
Suma zbiorów spójnych nie musi być zbiorem | Suma zbiorów spójnych nie musi być zbiorem | ||
spójnym. Wystarczy wziąć dwa przedziały w <math> | spójnym. Wystarczy wziąć dwa przedziały w <math>\mathbb{R}</math>: | ||
<math> | <math>A=(0,1)</math> i <math>B=(2,3)</math> (są to zbiory spójne; | ||
porównaj [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_25|twierdzenia 1.25.]]). | porównaj [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_25|twierdzenia 1.25.]]). | ||
Ich suma <math> | Ich suma <math>A\cup B=(0,1)\cup (2,3)</math> nie jest zbiorem spójnym, | ||
gdyż nie jest przedziałem. | gdyż nie jest przedziałem. | ||
Oczywiście, aby zachodził kontrprzykład, zbiory <math> | Oczywiście, aby zachodził kontrprzykład, zbiory <math>A</math> i <math>B</math> muszą | ||
być rozłączne. W przeciwnym razie z [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_26|twierdzenia 1.26.]] | być rozłączne. W przeciwnym razie z [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_26|twierdzenia 1.26.]] | ||
wynikałoby, że suma jest zbiorem spójnym.<br> | wynikałoby, że suma jest zbiorem spójnym.<br> | ||
Jeśli zbiór <math> | Jeśli zbiór <math>A\cup B</math> jest spójny, to zbiory <math>A</math> i <math>B</math> nie | ||
muszą być spójne. Jako przykład weźmy zbiory | muszą być spójne. Jako przykład weźmy zbiory | ||
<math> | <math>A=(1,3)\cup (4,7)</math> oraz <math>B=[2,5]\cup [6,8]</math>. | ||
Wówczas zbiory <math> | Wówczas zbiory <math>A,B\subseteq \mathbb{R}</math> nie są spójne, ale | ||
zbiór <math> | zbiór <math>A\cup B=(1,8]</math> jest spójny | ||
(patrz [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_26|twierdzenia 1.26.]]).<br> | (patrz [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_26|twierdzenia 1.26.]]).<br> | ||
{| border="0" align="center" cellspacing="10" | {| border="0" align="center" cellspacing="10" | ||
| | |[[File:Am2.M02.C.R01.svg|375x375px|thumb|center|Przeciecie zbiorów <math>A</math> i <math>B</math>]] | ||
|[[File:Am2.M02.C.R02.svg|375x151px|thumb|center|Suma zbiorów spójnych nie musi być zbiorem spójnym]] | |||
< | [[File:Am2.M02.C.R03.svg|375x151px|thumb|center|Ze spójności sumy zbiorów nie wynika spójność ich składowych]] | ||
< | |||
| | |||
|} | |} | ||
</div></div> | </div></div> | ||
| Linia 373: | Linia 361: | ||
{{cwiczenie|2.7.|cw_2_7| | {{cwiczenie|2.7.|cw_2_7| | ||
Niech <math> | Niech <math>X</math> będzie przestrzenią metryczną | ||
oraz <math> | oraz <math>A,B\subseteq X</math>. Które z implikacji są prawdziwe:<br> | ||
"jeśli zbiory <math> | "jeśli zbiory <math>A</math> i <math>B</math> są zwarte, to zbiór <math>A\cup B</math> jest | ||
zwarty";<br> | zwarty";<br> | ||
"jeśli zbiór <math> | "jeśli zbiór <math>A\cup B</math> jest zwarty, to zbiory <math>A</math> i <math>B</math> są | ||
zwarte". | zwarte". | ||
}} | }} | ||
| Linia 383: | Linia 371: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Ewentualnych kontrprzykładów można szukać w | Ewentualnych kontrprzykładów można szukać w | ||
<math> | <math>\mathbb{R}</math>. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:Am2.M02.C.R04.svg|375x92px|thumb|right|Ze zwartości sumy zbiorów nie wynika zwartość ich składowych]] | |||
Jeśli zbiory <math> | Jeśli zbiory <math>A</math> i <math>B</math> są zwarte, to zbiór <math>A\cup B</math> jest | ||
zwarty. | zwarty. | ||
Aby to pokazać, weźmy dowolne pokrycie otwarte | Aby to pokazać, weźmy dowolne pokrycie otwarte | ||
<math> | <math>\{U_s\}_{s\in S}</math> | ||
zbioru <math> | zbioru <math>A\cup B</math>. Wówczas jest to zarówno pokrycie zbioru <math>A</math> | ||
jak i zbioru <math> | jak i zbioru <math>B</math>. Ponieważ zbiory <math>A</math> i <math>B</math> są zwarte, więc | ||
możemy wybrać podpokrycia skończone | możemy wybrać podpokrycia skończone | ||
<math> | <math>\{U_{s_i}\}_{i=1}^k</math> zbioru <math>A</math> oraz | ||
<math> | <math>\{U_{s_i}\}_{i=k+1}^l</math> zbioru <math>B</math>. | ||
Wówczas <math> | Wówczas <math>\{U_{s_i}\}_{i=1}^l</math> jest pokryciem skończonym zbioru <math>A\cup B</math> | ||
(jeśli zbiór otwarty powtarza się w pierwszym i drugim podpokryciu, | (jeśli zbiór otwarty powtarza się w pierwszym i drugim podpokryciu, | ||
to bierzemy go tylko raz w <math> | to bierzemy go tylko raz w <math>\{U_{s_i}\}_{i=1}^l</math>). | ||
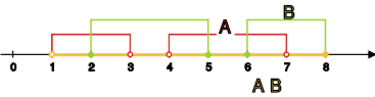
Jeśli zbiór <math> | Jeśli zbiór <math>A\cup B</math> jest zwarty, to zbiory <math>A</math> i <math>B</math> nie | ||
muszą być zwarte. Jako przykład weźmy przedziały w <math> | muszą być zwarte. Jako przykład weźmy przedziały w <math>\mathbb{R}</math>: | ||
<math> | <math>A=[1,3)</math> i <math>B=(2,4]</math>. Wówczas zbiory <math>A</math> i <math>B</math> nie są zwarte, | ||
ale zbiór <math> | ale zbiór <math>A\cup B</math> jest zwarty | ||
(patrz [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_21|twierdzenia 1.21.]]).<br> | (patrz [[Analiza matematyczna 2/Wykład 1: Przestrzenie metryczne#tw_1_21|twierdzenia 1.21.]]).<br> | ||
</div></div> | </div></div> | ||
| Linia 420: | Linia 405: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Wziąć <math> | Wziąć <math>\varepsilon=\frac{1}{2}</math> i zastosować w definicji ciągu Cauchy'ego. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>\{x_n\}</math> będzie ciągiem Cauchy'ego przestrzeni metrycznej | ||
dyskretnej. | dyskretnej. | ||
Wówczas w szczególności dla <math> | Wówczas w szczególności dla <math>\varepsilon=\frac{1}{2}</math> mamy | ||
<center> | <center> | ||
<math> | <math>\exists N\in\mathbb{N}\ \forall n,m\ge N: | ||
d(x_n,x_m)<\frac{1}{2} | d(x_n,x_m)<\frac{1}{2}</math> | ||
</math> | |||
</center> | </center> | ||
Ale metryka dyskretna przyjmuje tylko wartości <math> | Ale metryka dyskretna przyjmuje tylko wartości <math>0</math> i <math>1</math>, | ||
zatem dla dowolnych <math> | zatem dla dowolnych <math>n,m\ge N</math> mamy <math>d(x_n,x_m)=0</math>, | ||
a to z kolei oznacza, że <math> | a to z kolei oznacza, że <math>x_n=x_m</math>. | ||
Zatem pokazaliśmy, że | Zatem pokazaliśmy, że | ||
<center> | <center> | ||
<math> | <math>\forall n\ge N: | ||
x_n=x_N | x_n=x_N</math>, | ||
</math> | |||
</center> | </center> | ||
| Linia 457: | Linia 440: | ||
{{cwiczenie|2.9.|cw_2_9| | {{cwiczenie|2.9.|cw_2_9| | ||
Rozważmy płaszczyznę <math> | Rozważmy płaszczyznę <math>\mathbb{R}^2</math> z metryką kolejową z węzłem | ||
<math> | <math>O(0,0)</math>. | ||
Zbadać zbieżność dwóch ciągów: | Zbadać zbieżność dwóch ciągów: | ||
<math> | <math>\{x_n\}</math> i <math>\{y_x\}</math> w tej metryce, gdy | ||
<math> | <math>x_n=\bigg(\frac{1}{n},1\bigg)</math> oraz | ||
<math> | <math>y_n=\bigg(0,1+\frac{1}{n}\bigg)</math> dla <math>n\in\mathbb{N}</math>. | ||
}} | }} | ||
| Linia 473: | Linia 456: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
'''(1)''' Dla ciągu <math> | '''(1)''' Dla ciągu <math>\{x_n\}</math> zauważmy, że | ||
<center><math>\begin{array}{lll} | <center><math>\begin{array}{lll} | ||
d(x_n,x_{n+1})&=& | |||
d_2(x_n,\Theta)+d_2(x_{n+1},\Theta)\\ | |||
&=& | &=& | ||
\sqrt{\bigg(\frac{1}{n}\bigg)^2+1^2} | \sqrt{\bigg(\frac{1}{n}\bigg)^2+1^2} | ||
+ | + | ||
\sqrt{\bigg(\frac{1}{n+1}\bigg)^2+1^2} | \sqrt{\bigg(\frac{1}{n+1}\bigg)^2+1^2}\ge 2, | ||
\end{array}</math></center> | \end{array}</math></center> | ||
(gdzie <math> | (gdzie <math>\Theta</math> oznacza <math>((0,0)\in\mathbb{R}^2)</math>, | ||
zatem ciąg <math> | zatem ciąg <math>\{x_n\}</math> nie spełnia warunku Cauchy'ego, a zatem nie jest zbieżny.<br> | ||
<br> | <br> | ||
'''(2)''' | '''(2)''' | ||
Pokażemy, że ciąg <math> | Pokażemy, że ciąg <math>\{y_n\}</math> ma granicę | ||
<math> | <math>y_0=(0,1)</math>. Obliczmy | ||
<center><math> | <center><math>d(y_n,y_0) | ||
= | |||
d(y_n,y_0) | d(y_n,y_0) | ||
= | |||
\sqrt{0^2+\bigg(1+\frac{1}{n}-1\bigg)} | \sqrt{0^2+\bigg(1+\frac{1}{n}-1\bigg)} | ||
= | |||
\frac{1}{n} | \frac{1}{n}</math>,</center> | ||
</math></center> | |||
zatem <math> | zatem <math>d(y_n,y_0)\longrightarrow 0</math>, gdy <math>n\rightarrow +\infty</math>, | ||
a to oznacza, że <math> | a to oznacza, że <math>y_n\xrightarrow[d]{} y_0=(1,0)</math>. | ||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 21:46, 11 wrz 2023
Ciągi w przestrzeniach metrycznych
Ćwiczenie 2.1.
Niech będzie przestrzenią metryczną, niech będzie ciągiem oraz niech . Udowodnić, że jeśli oraz jest dowolnym podciągiem ciągu , to
Ćwiczenie 2.2.
Niech będzie przestrzenią metryczną, ciągiem oraz niech Udowodnić, że jeśli jest ciągiem zbieżnym oraz jest jego dowolnym podciągiem takim, że to także
Ćwiczenie 2.3.
Niech będą przestrzeniami metrycznymi dla ciągiem w
(w
szczególności
dla
oraz ).
Udowodnić, że:
(1)
,
wtedy i tylko wtedy, gdy
dla .
(2) Ciąg
spełnia warunek Cauchy'ego wtedy i tylko wtedy, gdy
ciągi spełniają warunek Cauchy'ego dla
Ćwiczenie 2.4.
Pokazać z definicji, że (z metryką euklidesową) nie jest zbiorem zwartym.
Ćwiczenie 2.5.
Jakie zbiory są zwarte w przestrzeni metrycznej dyskretnej? Odpowiedź uzasadnij.
Ćwiczenie 2.6.
Niech będzie przestrzenią metryczną
oraz . Które z implikacji są prawdziwe:
"jeśli zbiory i są spójne, to zbiór jest
spójny";
"jeśli zbiory i są spójne, to zbiór jest
spójny";
"jeśli zbiór jest spójny, to zbiory i są
spójne".
Ćwiczenie 2.7.
Niech będzie przestrzenią metryczną
oraz . Które z implikacji są prawdziwe:
"jeśli zbiory i są zwarte, to zbiór jest
zwarty";
"jeśli zbiór jest zwarty, to zbiory i są
zwarte".
Ćwiczenie 2.8.
Opisać jak wyglądają ciągi Cauchy'ego w przestrzeni metrycznej dyskretnej.
Ćwiczenie 2.9.
Rozważmy płaszczyznę z metryką kolejową z węzłem . Zbadać zbieżność dwóch ciągów: i w tej metryce, gdy oraz dla .