Programowanie funkcyjne/Procedury wyższych rzędów: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „<math> ” na „<math>” |
|||
| (Nie pokazano 24 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
==Wstęp== | ==Wstęp== | ||
<p align="justify"> | |||
Wcześniej zaznaczyliśmy, że procedury są w funkcyjnych językach programowania obywatelami pierwszej kategorii, | |||
czyli są równie dobrymi wartościami jak wszystkie inne. | |||
W szczególności procedury mogą być argumentami procedur lub ich wynikami. | |||
Argumenty proceduralne występują również w imperatywnych językach programowania (np. w standardzie Pascala). | |||
Natomiast to, że procedury mogą być wynikami procedur, jest czymś charakterystycznym dla języków funkcyjnych. | |||
W tym wykładzie zajmiemy się ''procedurami wyższych rzędów'', tzn. procedurami przetwarzającymi procedury. | |||
</p> | |||
{{uwaga||uwaga_parg| | |||
To, że w językach imperatywnych procedury mogą być przekazywane jako argumenty, a nie mogą być wynikami, wynika ze sposobu kompilacji programów imperatywnych. Czytelników, którzy znają techniki kompilacji prosimy o przypomnienie sobie, w jaki sposób przekazywane są argumenty proceduralne i porównanie tego z modelem obliczeń przedstawionym w kolejnym wykładzie.}} | |||
== | == Typy proceduralne i polimorfizm == | ||
=== | Przyjrzyjmy się kilku prostym przykładom procedur wyższych rzędów. | ||
'''let''' p f = function x -> f x + f (2 * x);; | |||
''val p : (int -> int) -> int -> int = <fun>'' | |||
<p align="justify"> | |||
Argumentem procedury <tt>p</tt> jest procedura <tt>f</tt>, | |||
natomiast jej wynikiem jest procedura będąca wartością <math>\lambda</math>-abstrakcji. | |||
Zwróćmy uwagę na typ procedury <tt>p</tt>. | |||
Możemy go przeczytać jako <tt>(int -> int) -> (int -> int)</tt>. | |||
Zarówno argument <tt>f</tt>, jak i wynik <tt>p</tt> są procedurami typu <tt>int -> int</tt>. | |||
</p> | |||
'''let''' twice f = '''function''' x -> f (f x);; | '''let''' twice f = '''function''' x -> f (f x);; | ||
'''''val''' twice : ('a -> 'a) -> 'a -> 'a = <fun>'' | '''''val''' twice : ('a -> 'a) -> 'a -> 'a = <fun>'' | ||
twice ('''function''' x -> x * (x+1)) 2;; | twice ('''function''' x -> x * (x+1)) 2;; | ||
''- : int = 42'' | ''- : int = 42'' | ||
twice (function s -> "mocium panie, " ^ s) "me wezwanie";; | |||
''- : string = "mocium panie, mocium panie, me wezwanie"'' | |||
<p align="justify"> | |||
Argumentem procedury <tt>twice</tt> jest procedura <tt>f</tt>, | |||
natomiast jej wynikiem jest złożenie <tt>f</tt> z samą sobą. | |||
Zwróćmy uwagę na typ procedury <tt>twice</tt>. | |||
Typ tej procedury czytamy jako: <tt>('a -> 'a) -> ('a -> 'a)</tt>. | |||
Kompilator jest w stanie wywnioskować, że <tt>f</tt> jest procedurą i że typ jej argumentu musi być taki sam, jak typ jej wyniku (inaczej nie możnaby jej złożyć samej ze sobą). | |||
Natomiast nie wie jaki to jest typ. | |||
Tak naprawdę, może to być dowolny typ. | |||
</p> | |||
<p align="justify"> | |||
Mamy tu do czynienia z ''polimorfizmem'' -- ta sama procedura może być '''wielu typów'''. | |||
Oznaczenie <tt>'a</tt> jest tzw. ''zmienną typową''. | |||
Jeśli w typie występują zmienne typowe, to taki typ jest schematem opisującym wiele typów. | |||
Do takiego typu-schematu pasuje każdy taki typ, który możemy z niego uzyskać, podstawiając (równocześnie) za zmienne typowe dowolne typy. | |||
Przy tym za różne zmienne typowe możemy podstawiać różne typy, ale za wszystkie wystąpienia tej samej zmiennej typowej musimy podstawiać te same typy. | |||
Na przykład, podstawiając za <tt>'a</tt> typ <tt>int</tt>, uzyskujemy z typu <tt>('a -> 'a) -> ('a -> 'a)</tt> | |||
typ <tt>(int -> int) -> (int -> int)</tt>. | |||
Natomiast podstawiając za <tt>'a</tt> typ <tt>'a -> 'a</tt>, uzyskujemy typ | |||
<tt>(('a -> 'a) -> ('a -> 'a)) -> (('a -> 'a) -> ('a -> 'a))</tt>. | |||
</p> | |||
{{uwaga||uwaga_podstawianie| | |||
Mechanizm podstawiania typów za zmienne typowe jest dokładnie taki sam, jak podstawianie termów, za zmienne w termach.}} | |||
=== | {{przyklad|[Dwakroć po dwakroć]||Spójrzmy na następujące zastosowanie <tt>twice</tt>:}} | ||
'''let''' czterokrotnie f = twice twice f;; | |||
''val czterokrotnie : ('a -> 'a) -> 'a -> 'a = <fun>'' | |||
Procedura <tt>czterokrotnie</tt> działa w następujący sposób: | |||
<center> | |||
<tt>czterokrotnie</tt> <i>f</i> = | |||
<tt>(twice twice)</tt> <i>f</i> = | |||
<tt>twice (twice</tt> <i>f</i><tt>)</tt> = | |||
<tt>twice</tt> <i>f</i> <sup>2</sup> = | |||
<i>f</i> <sup>4</sup> | |||
</center> | |||
<p align="justify"> | |||
Zwróćmy uwagę, że dwa wystąpienia <tt>twice</tt> w definicji <tt>czterokrotnie</tt> | |||
mają różne typy. | |||
Drugie wystąpienie operuje na funkcji <tt>f</tt>, | |||
a więc jest typu <tt>('a -> 'a) -> 'a -> 'a</tt>. | |||
Natomiast pierwsze wystąpienie <tt>twice</tt> przetwarza drugie, a więc jest typu | |||
<tt>(('a -> 'a) -> 'a -> 'a) -> ('a -> 'a) -> 'a -> 'a</tt>. | |||
Jest to możliwe dzięki polimorficzności procedury <tt>twice</tt>. | |||
</p> | |||
Składanie procedur możemy zdeiniować następująco: | |||
'''let''' compose f g = '''function''' x -> f (g x);; | '''let''' compose f g = '''function''' x -> f (g x);; | ||
''val compose : ('a -> 'b) -> ('c -> 'a) -> 'c -> 'b = <fun>'' | |||
<p align="justify"> | |||
Zwrócmy uwagę, że mamy tu aż trzy zmienne typowe. | |||
Mamy tu następujące zależności między typami składowych: | |||
* wynik <tt>g</tt> i argument <tt>f</tt> muszą być tego samego typu, | |||
* argument <tt>g</tt> i argument wyniku są tego samego typu, | |||
* wynik <tt>f</tt> i wynik wyniku <tt>compose</tt> są tego samego typu. | |||
Procedurę <tt>twice</tt> możemy teraz zdefiniować w następujący sposób: | |||
</p> | |||
'''let''' twice f = compose f f;; | '''let''' twice f = compose f f;; | ||
''val twice : ('a -> 'a) -> 'a -> 'a = <fun>'' | |||
= | <p align="justify"> | ||
Możemy też zdefiniować wielokrotne składanie funkcji: | |||
</p> | |||
'''let''' id x = x;; | '''let''' id x = x;; | ||
''val id : 'a -> 'a = <fun>'' | |||
'''let''' '''rec''' iterate n f = | '''let''' '''rec''' iterate n f = | ||
'''if''' n = 0 '''then''' id '''else''' compose (iterate (n-1) f) f;; | '''if''' n = 0 '''then''' id '''else''' compose (iterate (n-1) f) f;; | ||
''val iterate : int -> ('a -> 'a) -> 'a -> 'a = <fun>'' | |||
==Czy istnieją procedury wieloargumentowe?== | ==Czy istnieją procedury wieloargumentowe?== | ||
<p align="justify"> | |||
Typy proceduralne | Typy proceduralne są postaci <tt> argument -> wynik</tt>. | ||
Ponieważ zarówno argument, jak i wynik może być typu proceduralnego, więc typ może zawierać więcej "strzałek". Zastanówmy się nad typem procedur wieloargumentowych. | |||
Rozważmy następujące dwie definicje: | |||
</p> | |||
'''let''' plus (x, y) = x + y;; | '''let''' plus (x, y) = x + y;; | ||
'''''val''' plus : int * int -> int = <fun>'' | '''''val''' plus : int * int -> int = <fun>'' | ||
'''let''' plus x y = x + y;; | '''let''' plus x y = x + y;; | ||
'''''val''' plus : int -> int -> int = <fun>'' | '''''val''' plus : int -> int -> int = <fun>'' | ||
Pierwsza procedura | <p align="justify"> | ||
Pierwsza procedura ma jeden argument, który jest parą liczb całkowitych. | |||
Druga procedura ma dwa argumenty bedące liczbami całkowitymi. | |||
Jej typ można jednak zinterpretować tak: <tt>int -> (int -> int)</tt>. | |||
Można ją więc traktować jak procedurę '''jednoargumentową''', której wynikiem jest procedura jednoargumentowa, której wynikiem jest suma. | |||
Inaczej mówiąc, procedura ta bierze argumenty na raty. | |||
Przedstawiona powyżej definicja jest równoważna następującej, lepiej oddającej możliwość brania argumentów po jednym: | |||
</p> | |||
'''let''' plus = '''function''' x -> '''function''' y -> x + y;; | |||
''val plus : int -> int -> int = <fun>'' | |||
<p align="justify"> | |||
Można więc powiedzieć, że istnieją wyłącznie procedury jednoargumentowe, | |||
a procedury wieloargumentowe są tak naprawdę procedurami wyższego rzędu. | |||
Taki sposób patrzenia na procedury wieloargumentowe może być wygodny. | |||
Jeśli kolejność argumentów jest odpowiednio dobrana, to możemy czasem podawać tylko część z nich, | |||
otrzymując w wyniku potrzebną procedurę. | |||
</p> | |||
'''let''' plus x y = x + y;; | '''let''' plus x y = x + y;; | ||
'''''val''' plus : int -> int -> int = <fun>'' | |||
'''let''' inc = plus 1;; | '''let''' inc = plus 1;; | ||
''val inc : int -> int = <fun>'' | |||
Obie | |||
<p align="justify"> | |||
Obie przedstawione formy przekazywania argumentów są sobie równoważne. | |||
Dowodem na to są poniższe dwie procedury przekształcające jedną w postać w drugą i odwrotnie. | |||
Jakiego typu są te procedury? | Jakiego typu są te procedury? | ||
</p> | |||
'''let''' curry f = '''function''' x -> '''function''' y -> f (x, y);; | '''let''' curry f = '''function''' x -> '''function''' y -> f (x, y);; | ||
'''let''' uncurry f = '''function''' (x, y) -> f x y;; | '''let''' uncurry f = '''function''' (x, y) -> f x y;; | ||
<p align="justify"> | |||
Standardową postacią podawania argumentów procedury jest "curry". | |||
Tak więc przedstawione przykłady można zdefiniować i tak: | |||
</p> | |||
'''let''' twice f x = f (f x);; | '''let''' twice f x = f (f x);; | ||
| Linia 56: | Linia 171: | ||
==Przykład: Sumy częściowe szeregów== | ==Przykład: Sumy częściowe szeregów== | ||
<p align="justify"> | |||
Powiedzmy, że interesuje nas przybliżanie szeregów przez obliczanie ich sum częściowych. | |||
Możemy zdefiniować procedurę obliczającą sumę częściową dowolnego szeregu. | |||
Jej parametrem jest procedura zwracająca określony element szeregu. | |||
</p> | |||
'''let''' '''rec''' szereg f n = | |||
'''if''' n = 0 '''then''' 0.0 '''else''' f n +. szereg f (n-1);; | |||
''val szereg : (int -> float) -> int -> float = <fun>'' | |||
<p align="justify"> | |||
Powiedzmy, że chcemy przybliżać szereg <math>\sum_{i=1}^{\infty} \frac{1}{(4i-3)(4i-1)} = \frac{\pi}{8}</math>. | |||
Żeby móc liczyć sumy częściowe tego szeregu, wystarczy, że opiszemy jego elementy. | |||
</p> | |||
'''let''' szereg_pi_8 n = | '''let''' szereg_pi_8 n = | ||
szereg | |||
('''function''' i -> 1. /. ((4. *. float i -. 3.) *. (4. *. float i -. 1.))) | |||
n;; | |||
''val szereg_pi_8 : int -> float = <fun>'' | |||
'''let''' pi = 8. *. szereg_pi_8 1000;; | '''let''' pi = 8. *. szereg_pi_8 1000;; | ||
''val pi : float = 3.14109265362103818'' | |||
Procedura | |||
<p align="justify"> | |||
Procedura <tt>szereg</tt> może służyć do obliczania sumczęściowych dowolnych szeregów. | |||
Żeby jednak dokonać takiej abstrakcji, musi ona mieć parametr proceduralny. | |||
</p> | |||
==Przykład: Różniczkowanie funkcji== | ==Przykład: Różniczkowanie funkcji== | ||
| Linia 77: | Linia 204: | ||
'''let''' rozniczka f x dx = (f (x +. dx) -. f x) /. dx;; | '''let''' rozniczka f x dx = (f (x +. dx) -. f x) /. dx;; | ||
''val rozniczka : (float -> float) -> float -> float -> float = <fun>'' | |||
Wówczas pochodną możemy przybliżyć następująco: | Wówczas pochodną możemy przybliżyć następująco: | ||
'''let''' epsilon = 0.00000001;; | |||
''val epsilon : float = 1e-08'' | |||
'''let''' pochodna f x = rozniczka f x epsilon;; | '''let''' pochodna f x = rozniczka f x epsilon;; | ||
''val pochodna : (float -> float) -> float -> float = <fun>'' | |||
<p align="justify"> | |||
Zwróćmy uwagę, że <tt>pochodna</tt> jest procedurą jednoargumentową i wynikiem <tt>(pochodna f)</tt> jest funkcja będąca pochodną <tt>f</tt>. | Zwróćmy uwagę, że <tt>pochodna</tt> jest procedurą jednoargumentową i wynikiem <tt>(pochodna f)</tt> jest funkcja będąca pochodną <tt>f</tt>. | ||
Czyli na procedurę <tt>pochodna</tt> możemy patrzeć albo jak na procedurę dwuargumentową, której wynikiem jest przybliżenie pochodnej danej funkcji w punkcie, albo jak na procedurę jednoargumentową, której wynikiem jest funkcja będąca pochodną danej funkcji. | |||
</p> | |||
== | pochodna (function x -> x) 42.69;; | ||
''- : float = 1.000000082740371'' | |||
let g = pochodna (function x -> 7.0 *. x *. x +. 5.0);; | |||
''val g : float -> float = <fun>'' | |||
g 3.0;; | |||
''- : float = 41.9999992118391674'' | |||
==Przykład: Metoda Newtona== | |||
<p align="justify"> | |||
Metoda Newtona, nazywana też metodą stycznych, służy przybliżaniu zer danych funkcji. | |||
Zakładamy, że dana funkcja jest różniczkowalna. | |||
Pomijamy kwestię własności stopu przedstawionego algorytmu i ewentualnego dzielenia przez 0. | |||
Metoda Newtona działa w następujący sposób: w punkcie będącym aktualnym przybliżeniem zera funkcji | |||
rysujemy styczną do wykresu funkcji; kolejnym przybliżeniem jest punkt przecięcia stycznej z osią X. | |||
</p> | |||
[[Image:pf-rys-4-1.gif||center]] | |||
Jest to przykład algorytmu polegającego na iteracyjnym przybliżaniu wyniku. Spróbujmy sformułować | <p align="justify"> | ||
postępowania iteracyjnego: | Jest to przykład algorytmu polegającego na iteracyjnym przybliżaniu wyniku. | ||
Spróbujmy sformułować ogólny schemat takiego postępowania iteracyjnego: | |||
</p> | |||
'''let''' '''rec''' iteruj poczatek popraw czy_dobre wynik = | '''let''' '''rec''' iteruj poczatek popraw czy_dobre wynik = | ||
| Linia 100: | Linia 249: | ||
'''else''' | '''else''' | ||
iteruj (popraw poczatek) popraw czy_dobre wynik;; | iteruj (popraw poczatek) popraw czy_dobre wynik;; | ||
''val iteruj : 'a -> ('a -> 'a) -> ('a -> bool) -> ('a -> 'b) -> 'b = <fun>'' | |||
Zastosujmy teraz ten schemat do zaimplementowania metody stycznych Newtona. Zauważmy, że jeżeli naszym przybliżeniem zera jest <math> x </math>, to styczna do wykresu funkcji przecina oś X w punkcie <math> x - \frac{(f\ x)}{(f'\ x)}</math>. | |||
<p align="justify"> | |||
Zastosujmy teraz ten schemat do zaimplementowania metody stycznych Newtona. | |||
Zauważmy, że jeżeli naszym przybliżeniem zera jest <math>x</math>, to styczna do wykresu funkcji przecina oś X w punkcie <math>x - \frac{(f\ x)}{(f'\ x)}</math>. | |||
</p> | |||
'''let''' id x = x;; | '''let''' id x = x;; | ||
''val id : 'a -> 'a = <fun>'' | |||
'''let''' newton f x = | '''let''' newton f x = | ||
'''let''' p = pochodna f | '''let''' p = pochodna f | ||
'''in''' | '''in''' | ||
'''let''' czy_dobre x = | '''let''' czy_dobre x = abs_float (f x) < epsilon | ||
'''and''' popraw x = x -. (f x) /. (p x) | '''and''' popraw x = x -. (f x) /. (p x) | ||
'''in''' | '''in''' | ||
iteruj x popraw czy_dobre id;; | iteruj x popraw czy_dobre id;; | ||
''val newton : (float -> float) -> float -> float = <fun>'' | |||
Zwróćmy uwagę na to, że procedura <tt>popraw-newton</tt> jest lokalna i ma dostęp do funkcji <tt>f</tt>. | |||
<p align="justify"> | |||
Zwróćmy uwagę na to, że procedura <tt>popraw-newton</tt> jest lokalna i ma dostęp do funkcji <tt>f</tt>. | |||
Procedura <tt>pochodna</tt> pochodzi z poprzedniego przykładu. | |||
</p> | |||
<p align="justify"> | |||
Pod nazwą "metoda Newtona" znana jest też metoda liczenia pierwiastków kwadratowych. | |||
Jest to szczególny przypadek metody Newtona znajdowania zer, dla funkcji <math>f(x) = x^2 - a</math>. | |||
Funkcja ta ma zera w punktach <math>\pm \sqrt{a}</math>. | |||
Ponadto <math>f'(x) = 2x</math>, czyli nasz algorytm przekształca przybliżenie <math>x</math> w: | |||
</p> | |||
<center><math> | <center><math> | ||
| Linia 122: | Linia 288: | ||
</math></center> | </math></center> | ||
Zaczynając w punkcie 1 przybliżamy <math> \sqrt{a}</math>. | <p align="justify"> | ||
czyli dokładnie tak, jak to ma miejsce w metodzie Newtona przybliżania pierwiastków kwadratowych. | |||
Zaczynając w punkcie 1 przybliżamy <math>\sqrt{a}</math>. | |||
</p> | |||
'''let''' sqrt a = | '''let''' sqrt a = | ||
'''let''' f x = a -. | '''let''' f x = a -. x *. x | ||
'''in''' newton f 1.;; | '''in''' newton f 1.;; | ||
''val sqrt : float -> float = <fun>'' | |||
sqrt 17.64;; | |||
''- : float = 4.20000000000023643'' | |||
==Punkty stałe funkcji== | <p align="justify"> | ||
Zauważmy, że większość zdefiniowanych w tym przykładzie procedur to procedury wyższych rzędów. | |||
</p> | |||
== Przykład: Punkty stałe funkcji == | |||
<p align="justify"> | |||
Punkt stały funkcji <math>f</math> to taki <math>x</math>, że <math>f(x) = x</math>. | |||
W przypadku niektórych funkcji (i określonych <math>x</math>-ów) ciąg <math>x, f(x), f^2(x), f^3(x), \dots</math> jest zbieżny do pewnego punktu stałego <math>f</math>. | |||
Jest tak np.\ jeżeli <math>f</math> jest przekształceniem zwężającym. | |||
Możemy zaimplementować tę metodę przybliżania punktów stałych. | |||
Zastosujemy tutaj procedurę <tt>iteruj</tt> z poprzedniego przykładu: | |||
</p> | |||
'''let''' punkt_staly f x = | '''let''' punkt_staly f x = | ||
'''let''' blisko x = | '''let''' blisko x = abs_float (x -. f x) < epsilon | ||
'''in''' | '''in''' | ||
iteruj x f blisko f;; | iteruj x f blisko f;; | ||
''val punkt_staly : (float -> float) -> float -> float = <fun>'' | |||
Przykładową funkcją, której punkt stały można znaleźć tą metodą jest <math> \cos(x)</math>. | Przykładową funkcją, której punkt stały można znaleźć tą metodą jest <math>\cos(x)</math>. | ||
punkt_staly cos 1.0;; | punkt_staly cos 1.0;; | ||
''0.73908 | ''- : float = 0.73908...'' | ||
Proszę to sprawdzić na jakimś nudnym wykładzie | <p align="justify"> | ||
Proszę to sprawdzić na jakimś nudnym wykładzie -- wystarczy najpierw nacisnąć 1, a potem ciągle stukać w klawisz <math>\cos</math>. | |||
</p> | |||
Obliczanie punktów stałych moglibyśmy zastosować do obliczania pierwiastków --- punkt stały funkcji <math> y \to \frac{x}{y}</math> to <math> \sqrt{x}</math>. Jednak obliczenie: | <p align="justify"> | ||
Obliczanie punktów stałych moglibyśmy zastosować do obliczania pierwiastków --- | |||
punkt stały funkcji <math>y \to \frac{x}{y}</math> to <math>\sqrt{x}</math>. | |||
Jednak obliczenie: | |||
</p> | |||
punkt_staly (function y -> x /. y) 1.0;; | punkt_staly (function y -> x /. y) 1.0;; | ||
nie jest zbieżne: | nie jest zbieżne: | ||
<math> | <math> | ||
1 \to \frac{x}{1} = x \to \frac{x}{x} = 1 \to \dots | 1 \to \frac{x}{1} = x \to \frac{x}{x} = 1 \to \dots | ||
</math> | </math> | ||
W takich przypadkach czasami pomaga " | <p align="justify"> | ||
W takich przypadkach czasami pomaga technika nazywana "wytłumieniem przez uśrednienie". | |||
Uśrednienie funkcji <math>f</math>, to funkcja <math>x \mapsto \frac{f(x) + x}{2}</math>. | |||
Zauważmy, że dla dowolnej funkcji <math>f</math>, ma ona dokładnie takie same punkty stałe jak jej uśrednienie. | |||
Zamiast więc szukać punktów stałych <math>f</math>, możemy szukać punktów stałych uśrednienia <math>f</math>. | |||
</p> | |||
'''let''' usrednienie f = | '''let''' usrednienie f = | ||
'''function''' x -> average x (f x);; | |||
''val usrednienie : (float -> float) -> float -> float = <fun>'' | |||
'''let''' sqrt x = | '''let''' sqrt x = | ||
punkt_staly (usrednienie ('''function''' y -> x /. y)) 1.0;; | |||
''val sqrt : float -> float = <fun>'' | |||
<p align="justify"> | |||
Jeśli zanalizujemy działanie powyższej procedury <tt>sqrt</tt>, to okaże się, że | |||
znowu uzyskaliśmy metodę pierwiastkowania Newtona. | |||
</p> | |||
==Zastosowania procedur wyższych rzędów== | ==Zastosowania procedur wyższych rzędów== | ||
<p align="justify"> | |||
Procedury wyższych rzędów to jeden z tych elementów języka, który jest czysto funkcyjny. | |||
W językach imperatywnych procedury mogą być parametrami procedur, lecz nie wynikami. | |||
W przypadku języków funkcyjnych mamy pełną swobodę. | |||
Procedury mają tu te same prawa, co inne wartości. | |||
</p> | |||
<p align="justify"> | |||
Zastosowania procedur wyższych rzędów można podzielić na trzy grupy: | |||
Zastosowania procedur wyższych rzędów można podzielić na | |||
* Pewne pojęcia matematyczne, zwłaszcza te dotyczące funkcji, w naturalny sposób przekładają się na procedury wyższych rzędów, np.: sumy częściowe szeregów, składanie funkcji, różniczkowanie funkcji itp. | * Pewne pojęcia matematyczne, zwłaszcza te dotyczące funkcji, w naturalny sposób przekładają się na procedury wyższych rzędów, np.: sumy częściowe szeregów, składanie funkcji, różniczkowanie funkcji itp. | ||
* Procedury są jeszcze jednym typem danych. Przyjmując takie podejście, procedury przetwarzające | * Procedury są jeszcze jednym typem danych. Przyjmując takie podejście, procedury przetwarzające dane, jeśli te dane będą akurat procedurami, same będą procedurami wyższych rzędów. | ||
* Procedury wyższych rzędów są również narzędziem abstrakcji. Jeżeli ten sam fragment kodu pojawia się w kilku miejscach, to naturalnym jest wyłonienie go w postaci (zwykłej) procedury. | * Procedury wyższych rzędów są również narzędziem abstrakcji. Jeżeli ten sam fragment kodu pojawia się w kilku miejscach, to naturalnym jest wyłonienie go w postaci (zwykłej) procedury. Jeżeli natomiast ten sam schemat kodu pojawia się w wielu miejscach, ale różni się wypełniającymi go fragmentami, to schemat ten możemy ująć w postaci procedury wyższego rzędu, a fragmenty do wypełnienia staną się parametrami proceduralnymi. Przykładem może być tu procedura <tt>iteruj</tt>. | ||
</p> | |||
== | == Ćwiczenia == | ||
[[Programowanie funkcyjne/Procedury wyższych rzędów/Ćwiczenia | [[Programowanie funkcyjne/Procedury wyższych rzędów/Ćwiczenia |Ćwiczenia]] | ||
Aktualna wersja na dzień 22:16, 11 wrz 2023
Wstęp
Wcześniej zaznaczyliśmy, że procedury są w funkcyjnych językach programowania obywatelami pierwszej kategorii, czyli są równie dobrymi wartościami jak wszystkie inne. W szczególności procedury mogą być argumentami procedur lub ich wynikami. Argumenty proceduralne występują również w imperatywnych językach programowania (np. w standardzie Pascala). Natomiast to, że procedury mogą być wynikami procedur, jest czymś charakterystycznym dla języków funkcyjnych. W tym wykładzie zajmiemy się procedurami wyższych rzędów, tzn. procedurami przetwarzającymi procedury.
Typy proceduralne i polimorfizm
Przyjrzyjmy się kilku prostym przykładom procedur wyższych rzędów.
let p f = function x -> f x + f (2 * x);; val p : (int -> int) -> int -> int = <fun>
Argumentem procedury p jest procedura f, natomiast jej wynikiem jest procedura będąca wartością -abstrakcji. Zwróćmy uwagę na typ procedury p. Możemy go przeczytać jako (int -> int) -> (int -> int). Zarówno argument f, jak i wynik p są procedurami typu int -> int.
let twice f = function x -> f (f x);;
val twice : ('a -> 'a) -> 'a -> 'a = <fun>
twice (function x -> x * (x+1)) 2;;
- : int = 42
twice (function s -> "mocium panie, " ^ s) "me wezwanie";;
- : string = "mocium panie, mocium panie, me wezwanie"
Argumentem procedury twice jest procedura f, natomiast jej wynikiem jest złożenie f z samą sobą. Zwróćmy uwagę na typ procedury twice. Typ tej procedury czytamy jako: ('a -> 'a) -> ('a -> 'a). Kompilator jest w stanie wywnioskować, że f jest procedurą i że typ jej argumentu musi być taki sam, jak typ jej wyniku (inaczej nie możnaby jej złożyć samej ze sobą). Natomiast nie wie jaki to jest typ. Tak naprawdę, może to być dowolny typ.
Mamy tu do czynienia z polimorfizmem -- ta sama procedura może być wielu typów. Oznaczenie 'a jest tzw. zmienną typową. Jeśli w typie występują zmienne typowe, to taki typ jest schematem opisującym wiele typów. Do takiego typu-schematu pasuje każdy taki typ, który możemy z niego uzyskać, podstawiając (równocześnie) za zmienne typowe dowolne typy. Przy tym za różne zmienne typowe możemy podstawiać różne typy, ale za wszystkie wystąpienia tej samej zmiennej typowej musimy podstawiać te same typy. Na przykład, podstawiając za 'a typ int, uzyskujemy z typu ('a -> 'a) -> ('a -> 'a) typ (int -> int) -> (int -> int). Natomiast podstawiając za 'a typ 'a -> 'a, uzyskujemy typ (('a -> 'a) -> ('a -> 'a)) -> (('a -> 'a) -> ('a -> 'a)).
Przykład [Dwakroć po dwakroć]
let czterokrotnie f = twice twice f;;
val czterokrotnie : ('a -> 'a) -> 'a -> 'a = <fun>
Procedura czterokrotnie działa w następujący sposób:
czterokrotnie f = (twice twice) f = twice (twice f) = twice f 2 = f 4
Zwróćmy uwagę, że dwa wystąpienia twice w definicji czterokrotnie mają różne typy. Drugie wystąpienie operuje na funkcji f, a więc jest typu ('a -> 'a) -> 'a -> 'a. Natomiast pierwsze wystąpienie twice przetwarza drugie, a więc jest typu (('a -> 'a) -> 'a -> 'a) -> ('a -> 'a) -> 'a -> 'a. Jest to możliwe dzięki polimorficzności procedury twice.
Składanie procedur możemy zdeiniować następująco:
let compose f g = function x -> f (g x);;
val compose : ('a -> 'b) -> ('c -> 'a) -> 'c -> 'b = <fun>
Zwrócmy uwagę, że mamy tu aż trzy zmienne typowe. Mamy tu następujące zależności między typami składowych:
- wynik g i argument f muszą być tego samego typu,
- argument g i argument wyniku są tego samego typu,
- wynik f i wynik wyniku compose są tego samego typu.
Procedurę twice możemy teraz zdefiniować w następujący sposób:
let twice f = compose f f;;
val twice : ('a -> 'a) -> 'a -> 'a = <fun>
Możemy też zdefiniować wielokrotne składanie funkcji:
let id x = x;;
val id : 'a -> 'a = <fun>
let rec iterate n f =
if n = 0 then id else compose (iterate (n-1) f) f;;
val iterate : int -> ('a -> 'a) -> 'a -> 'a = <fun>
Czy istnieją procedury wieloargumentowe?
Typy proceduralne są postaci argument -> wynik. Ponieważ zarówno argument, jak i wynik może być typu proceduralnego, więc typ może zawierać więcej "strzałek". Zastanówmy się nad typem procedur wieloargumentowych. Rozważmy następujące dwie definicje:
let plus (x, y) = x + y;; val plus : int * int -> int = <fun> let plus x y = x + y;; val plus : int -> int -> int = <fun>
Pierwsza procedura ma jeden argument, który jest parą liczb całkowitych. Druga procedura ma dwa argumenty bedące liczbami całkowitymi. Jej typ można jednak zinterpretować tak: int -> (int -> int). Można ją więc traktować jak procedurę jednoargumentową, której wynikiem jest procedura jednoargumentowa, której wynikiem jest suma. Inaczej mówiąc, procedura ta bierze argumenty na raty. Przedstawiona powyżej definicja jest równoważna następującej, lepiej oddającej możliwość brania argumentów po jednym:
let plus = function x -> function y -> x + y;; val plus : int -> int -> int = <fun>
Można więc powiedzieć, że istnieją wyłącznie procedury jednoargumentowe, a procedury wieloargumentowe są tak naprawdę procedurami wyższego rzędu. Taki sposób patrzenia na procedury wieloargumentowe może być wygodny. Jeśli kolejność argumentów jest odpowiednio dobrana, to możemy czasem podawać tylko część z nich, otrzymując w wyniku potrzebną procedurę.
let plus x y = x + y;; val plus : int -> int -> int = <fun> let inc = plus 1;; val inc : int -> int = <fun>
Obie przedstawione formy przekazywania argumentów są sobie równoważne. Dowodem na to są poniższe dwie procedury przekształcające jedną w postać w drugą i odwrotnie. Jakiego typu są te procedury?
let curry f = function x -> function y -> f (x, y);; let uncurry f = function (x, y) -> f x y;;
Standardową postacią podawania argumentów procedury jest "curry". Tak więc przedstawione przykłady można zdefiniować i tak:
let twice f x = f (f x);; let compose f g x = f (g x);; let curry f x y = f (x, y);; let uncurry f (x, y) = f x y;;
Przykład: Sumy częściowe szeregów
Powiedzmy, że interesuje nas przybliżanie szeregów przez obliczanie ich sum częściowych. Możemy zdefiniować procedurę obliczającą sumę częściową dowolnego szeregu. Jej parametrem jest procedura zwracająca określony element szeregu.
let rec szereg f n = if n = 0 then 0.0 else f n +. szereg f (n-1);; val szereg : (int -> float) -> int -> float = <fun>
Powiedzmy, że chcemy przybliżać szereg . Żeby móc liczyć sumy częściowe tego szeregu, wystarczy, że opiszemy jego elementy.
let szereg_pi_8 n =
szereg
(function i -> 1. /. ((4. *. float i -. 3.) *. (4. *. float i -. 1.)))
n;;
val szereg_pi_8 : int -> float = <fun>
let pi = 8. *. szereg_pi_8 1000;;
val pi : float = 3.14109265362103818
Procedura szereg może służyć do obliczania sumczęściowych dowolnych szeregów. Żeby jednak dokonać takiej abstrakcji, musi ona mieć parametr proceduralny.
Przykład: Różniczkowanie funkcji
Zdefiniujmy najpierw różniczkę:
let rozniczka f x dx = (f (x +. dx) -. f x) /. dx;; val rozniczka : (float -> float) -> float -> float -> float = <fun>
Wówczas pochodną możemy przybliżyć następująco:
let epsilon = 0.00000001;; val epsilon : float = 1e-08 let pochodna f x = rozniczka f x epsilon;; val pochodna : (float -> float) -> float -> float = <fun>
Zwróćmy uwagę, że pochodna jest procedurą jednoargumentową i wynikiem (pochodna f) jest funkcja będąca pochodną f. Czyli na procedurę pochodna możemy patrzeć albo jak na procedurę dwuargumentową, której wynikiem jest przybliżenie pochodnej danej funkcji w punkcie, albo jak na procedurę jednoargumentową, której wynikiem jest funkcja będąca pochodną danej funkcji.
pochodna (function x -> x) 42.69;; - : float = 1.000000082740371 let g = pochodna (function x -> 7.0 *. x *. x +. 5.0);; val g : float -> float = <fun> g 3.0;; - : float = 41.9999992118391674
Przykład: Metoda Newtona
Metoda Newtona, nazywana też metodą stycznych, służy przybliżaniu zer danych funkcji. Zakładamy, że dana funkcja jest różniczkowalna. Pomijamy kwestię własności stopu przedstawionego algorytmu i ewentualnego dzielenia przez 0. Metoda Newtona działa w następujący sposób: w punkcie będącym aktualnym przybliżeniem zera funkcji rysujemy styczną do wykresu funkcji; kolejnym przybliżeniem jest punkt przecięcia stycznej z osią X.
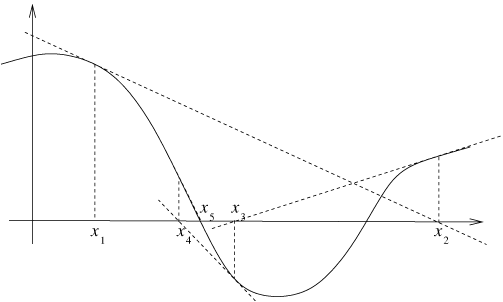
Jest to przykład algorytmu polegającego na iteracyjnym przybliżaniu wyniku. Spróbujmy sformułować ogólny schemat takiego postępowania iteracyjnego:
let rec iteruj poczatek popraw czy_dobre wynik =
if czy_dobre poczatek then
wynik poczatek
else
iteruj (popraw poczatek) popraw czy_dobre wynik;;
val iteruj : 'a -> ('a -> 'a) -> ('a -> bool) -> ('a -> 'b) -> 'b = <fun>
Zastosujmy teraz ten schemat do zaimplementowania metody stycznych Newtona. Zauważmy, że jeżeli naszym przybliżeniem zera jest , to styczna do wykresu funkcji przecina oś X w punkcie .
let id x = x;; val id : 'a -> 'a = <fun> let newton f x = let p = pochodna f in let czy_dobre x = abs_float (f x) < epsilon and popraw x = x -. (f x) /. (p x) in iteruj x popraw czy_dobre id;; val newton : (float -> float) -> float -> float = <fun>
Zwróćmy uwagę na to, że procedura popraw-newton jest lokalna i ma dostęp do funkcji f. Procedura pochodna pochodzi z poprzedniego przykładu.
Pod nazwą "metoda Newtona" znana jest też metoda liczenia pierwiastków kwadratowych. Jest to szczególny przypadek metody Newtona znajdowania zer, dla funkcji . Funkcja ta ma zera w punktach . Ponadto , czyli nasz algorytm przekształca przybliżenie w:
czyli dokładnie tak, jak to ma miejsce w metodzie Newtona przybliżania pierwiastków kwadratowych. Zaczynając w punkcie 1 przybliżamy .
let sqrt a = let f x = a -. x *. x in newton f 1.;; val sqrt : float -> float = <fun> sqrt 17.64;; - : float = 4.20000000000023643
Zauważmy, że większość zdefiniowanych w tym przykładzie procedur to procedury wyższych rzędów.
Przykład: Punkty stałe funkcji
Punkt stały funkcji to taki , że . W przypadku niektórych funkcji (i określonych -ów) ciąg jest zbieżny do pewnego punktu stałego . Jest tak np.\ jeżeli jest przekształceniem zwężającym. Możemy zaimplementować tę metodę przybliżania punktów stałych. Zastosujemy tutaj procedurę iteruj z poprzedniego przykładu:
let punkt_staly f x =
let blisko x = abs_float (x -. f x) < epsilon
in
iteruj x f blisko f;;
val punkt_staly : (float -> float) -> float -> float = <fun>
Przykładową funkcją, której punkt stały można znaleźć tą metodą jest .
punkt_staly cos 1.0;; - : float = 0.73908...
Proszę to sprawdzić na jakimś nudnym wykładzie -- wystarczy najpierw nacisnąć 1, a potem ciągle stukać w klawisz .
Obliczanie punktów stałych moglibyśmy zastosować do obliczania pierwiastków --- punkt stały funkcji to . Jednak obliczenie:
punkt_staly (function y -> x /. y) 1.0;;
nie jest zbieżne:
W takich przypadkach czasami pomaga technika nazywana "wytłumieniem przez uśrednienie". Uśrednienie funkcji , to funkcja . Zauważmy, że dla dowolnej funkcji , ma ona dokładnie takie same punkty stałe jak jej uśrednienie. Zamiast więc szukać punktów stałych , możemy szukać punktów stałych uśrednienia .
let usrednienie f = function x -> average x (f x);; val usrednienie : (float -> float) -> float -> float = <fun> let sqrt x = punkt_staly (usrednienie (function y -> x /. y)) 1.0;; val sqrt : float -> float = <fun>
Jeśli zanalizujemy działanie powyższej procedury sqrt, to okaże się, że znowu uzyskaliśmy metodę pierwiastkowania Newtona.
Zastosowania procedur wyższych rzędów
Procedury wyższych rzędów to jeden z tych elementów języka, który jest czysto funkcyjny. W językach imperatywnych procedury mogą być parametrami procedur, lecz nie wynikami. W przypadku języków funkcyjnych mamy pełną swobodę. Procedury mają tu te same prawa, co inne wartości.
Zastosowania procedur wyższych rzędów można podzielić na trzy grupy:
- Pewne pojęcia matematyczne, zwłaszcza te dotyczące funkcji, w naturalny sposób przekładają się na procedury wyższych rzędów, np.: sumy częściowe szeregów, składanie funkcji, różniczkowanie funkcji itp.
- Procedury są jeszcze jednym typem danych. Przyjmując takie podejście, procedury przetwarzające dane, jeśli te dane będą akurat procedurami, same będą procedurami wyższych rzędów.
- Procedury wyższych rzędów są również narzędziem abstrakcji. Jeżeli ten sam fragment kodu pojawia się w kilku miejscach, to naturalnym jest wyłonienie go w postaci (zwykłej) procedury. Jeżeli natomiast ten sam schemat kodu pojawia się w wielu miejscach, ale różni się wypełniającymi go fragmentami, to schemat ten możemy ująć w postaci procedury wyższego rzędu, a fragmenty do wypełnienia staną się parametrami proceduralnymi. Przykładem może być tu procedura iteruj.