Teoria kategorii dla informatyków/Ćwiczenia 11: Monady: Różnice pomiędzy wersjami
mNie podano opisu zmian |
|||
| Linia 1: | Linia 1: | ||
==Zadanie 11.1== {{kotwica|mod11:zad1|}} | ==Zadanie 11.1== {{kotwica|mod11:zad1|}} | ||
| Linia 26: | Linia 25: | ||
<center>[[Grafika:tk-11.9.png]]</center> | <center>[[Grafika:tk-11.9.png]]</center> | ||
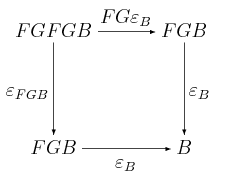
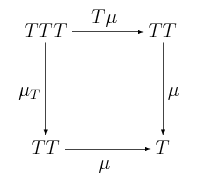
Pozbywając się nazw obiektów, podstawiając <math>\mu</math> za <math>G\varepsilon_F</math> oraz <math>T=GF</math> mamy na koniec: | Pozbywając się nazw obiektów, podstawiając <math>\mu</math> za <math>G\varepsilon_F</math> oraz <math>T=GF</math>, mamy na koniec: | ||
<center>[[Grafika:tk-11.10.png]]</center> | <center>[[Grafika:tk-11.10.png]]</center> | ||
| Linia 78: | Linia 77: | ||
<center>[[Grafika:tk-11.14.png]]</center> | <center>[[Grafika:tk-11.14.png]]</center> | ||
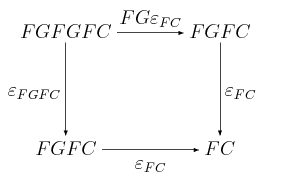
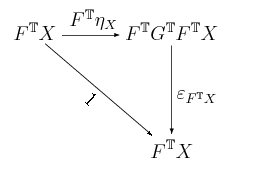
To kończy dowód, że <math>F^{\mathbb{T}}\dashv G^{\mathbb{T}}</math>. Indukowana monada to | To kończy dowód, że <math>F^{\mathbb{T}}\dashv G^{\mathbb{T}}</math>. Indukowana monada to: | ||
<center><math>(G^{\mathbb{T}}F^{\mathbb{T}}, \eta, G^{\mathbb{T}}\varepsilon_{^{\mathbb{T}}}) = (T,\eta,\mu)=\mathbb{T}.</math></center> | <center><math>(G^{\mathbb{T}}F^{\mathbb{T}}, \eta, G^{\mathbb{T}}\varepsilon_{^{\mathbb{T}}}) = (T,\eta,\mu)=\mathbb{T}.</math></center> | ||
| Linia 89: | Linia 88: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Wskazówka:''' <div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Wskazówka:''' <div class="mw-collapsible-content" style="display:none"> | ||
Wykorzystaj konstrukcję kategorii Eilenberga-Moore'a. Zauważ, że <math>P^{\mathbb{T}}</math> to poset izomorficzny z podzbiorem <math>P</math> składającym się z punktów stałych funkcji <math>T</math>. | Wykorzystaj konstrukcję kategorii Eilenberga - Moore'a. Zauważ, że <math>P^{\mathbb{T}}</math> to poset izomorficzny z podzbiorem <math>P</math> składającym się z punktów stałych funkcji <math>T</math>. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie:''' <div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie:''' <div class="mw-collapsible-content" style="display:none"> | ||
Po pierwsze, zobaczmy jak wyglądają <math>\mathbb{T}</math>-algebry. Są to pary <math>(x,Tx\leq x)</math> dla <math>x\in P</math>, czyli te spośród elementów <math>x\in P</math>, dla których prawdą jest, że <math>Tx\leq x</math>. Ale przecież własności monady implikują, że zawsze <math>x\leq Tx</math>, a zatem <math>\mathbb{T}</math>-algebry to punkty stałe funkcji <math>T</math> .Morfizm <math>\mathbb{T}</math>-algebr <math>(x,Tx\leq x)</math>, <math>(y,Ty\leq y)</math> istnieje, o ile <math>x\leq y</math>. A zatem <math>P^{\mathbb{T}}</math> jest częściowym porządkiem izomorficznym ze zbiorem <math>(\mathrm{fix}(T),\leq)</math> (punkty stałe <math>T</math> z porządkiem indukowanym z <math>P</math>). Funktor <math>G^{\mathbb{T}}</math>, który dla prostoty oznaczymy tu <math>g</math>, można zatem interpretować jako zanurzenie <math>g\colon \mathrm{fix}(T)\to P</math>. Funktor <math>F^{\mathbb{T}}</math>, oznaczany <math>f</math>, jest funkcją monotoniczną typu <math>P\to \mathrm{fix}(T)</math>, która każdemu elementowi <math>x\in P</math> przypisuje punkt stały <math>Tx\in P</math>. Wniosek: <math>f</math> jest obcięciem funkcji <math>T</math> do typu <math>P\to \mathrm{fix}(T)</math>. Oczywiście wtedy <math>fgx=x</math> dla dowolnego <math>x\in P</math>. Pokażmy, że <math>f\dashv g</math>, czyli dla dowolnych <math>a,b\in P</math>, <math>fa\leq b</math> wtedy i tylko wtedy, gdy <math>a\leq gb</math> w <math>P</math>. Załóżmy <math>fa\leq b</math>. Wówczas z monotoniczności <math>g</math> dostajemy <math>gfa\leq gb</math>. Z definicji monady wynika, że <math>a\leq Ta</math>, co czytamy też jako <math>a\leq gfa</math>, co w końcu daje: <math>a\leq gfa\leq gb</math>. Odwrotnie, załóżmy <math>a\leq gb</math>. Z monotoniczności <math>f</math> i faktu <math>fg=1_P</math>, co zauważyliśmy w poprzednim paragrafie, mamy natychmiast: <math>fa\leq fgb=1_Pb=b</math>. To kończy dowód faktu, że <math>f\dashv g</math>. </div></div> | Po pierwsze, zobaczmy jak wyglądają <math>\mathbb{T}</math>-algebry. Są to pary <math>(x,Tx\leq x)</math> dla <math>x\in P</math>, czyli te spośród elementów <math>x\in P</math>, dla których prawdą jest, że <math>Tx\leq x</math>. Ale przecież własności monady implikują, że zawsze <math>x\leq Tx</math>, a zatem <math>\mathbb{T}</math>-algebry to punkty stałe funkcji <math>T</math> .Morfizm <math>\mathbb{T}</math>-algebr <math>(x,Tx\leq x)</math>, <math>(y,Ty\leq y)</math> istnieje, o ile <math>x\leq y</math>. A zatem <math>P^{\mathbb{T}}</math> jest częściowym porządkiem izomorficznym ze zbiorem <math>(\mathrm{fix}(T),\leq)</math> (punkty stałe <math>T</math> z porządkiem indukowanym z <math>P</math>). Funktor <math>G^{\mathbb{T}}</math>, który dla prostoty oznaczymy tu <math>g</math>, można zatem interpretować jako zanurzenie <math>g\colon \mathrm{fix}(T)\to P</math>. Funktor <math>F^{\mathbb{T}}</math>, oznaczany <math>f</math>, jest funkcją monotoniczną typu <math>P\to \mathrm{fix}(T)</math>, która każdemu elementowi <math>x\in P</math> przypisuje punkt stały <math>Tx\in P</math>. Wniosek: <math>f</math> jest obcięciem funkcji <math>T</math> do typu <math>P\to \mathrm{fix}(T)</math>. Oczywiście wtedy <math>fgx=x</math> dla dowolnego <math>x\in P</math>. Pokażmy, że <math>f\dashv g</math>, czyli dla dowolnych <math>a,b\in P</math>, <math>fa\leq b</math> wtedy i tylko wtedy, gdy <math>a\leq gb</math> w <math>P</math>. Załóżmy <math>fa\leq b</math>. Wówczas z monotoniczności <math>g</math> dostajemy <math>gfa\leq gb</math>. Z definicji monady wynika, że <math>a\leq Ta</math>, co czytamy też jako <math>a\leq gfa</math>, co w końcu daje: <math>a\leq gfa\leq gb</math>. Odwrotnie, załóżmy <math>a\leq gb</math>. Z monotoniczności <math>f</math> i faktu <math>fg=1_P</math>, co zauważyliśmy w poprzednim paragrafie, mamy natychmiast: <math>fa\leq fgb=1_Pb=b</math>. To kończy dowód faktu, że: <math>f\dashv g</math>. </div></div> | ||
| Linia 130: | Linia 129: | ||
&=& \mu_X((1_M\times \eta_X)(e,x))\\ | &=& \mu_X((1_M\times \eta_X)(e,x))\\ | ||
&=& \mu_X((T\eta_X)(e,x))\\ | &=& \mu_X((T\eta_X)(e,x))\\ | ||
&=& (\mu_X\circ T\eta_X)(e,x)) | &=& (\mu_X\circ T\eta_X)(e,x)), | ||
\endaligned | \endaligned | ||
</math></center> | </math></center> | ||
co dowodzi, | co dowodzi, że <math>(\mu_X\circ \eta){TX})=1_{TX}=(\mu_X\circ T\eta_X)</math>. | ||
Po drugie | Po drugie: | ||
<center><math>\aligned | <center><math>\aligned | ||
| Linia 143: | Linia 142: | ||
&=& \mu_X(k,(m*n,x))\\ | &=& \mu_X(k,(m*n,x))\\ | ||
&=& (k*m*n,x))\\ | &=& (k*m*n,x))\\ | ||
&=& \mu_X((k*m,(n,x)))\\ &=& (\mu_X\circ\mu_{TX})(k,(m,(n,x))) | &=& \mu_X((k*m,(n,x)))\\ &=& (\mu_X\circ\mu_{TX})(k,(m,(n,x))), | ||
\endaligned</math></center> | \endaligned</math></center> | ||
| Linia 173: | Linia 172: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie:''' <div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie:''' <div class="mw-collapsible-content" style="display:none"> | ||
Algebrą dla tej monady jest każda para <math>(\mathcal{P} X,h\colon \mathcal{P} X\to X)</math>, która spełnia: <math>h(\{ x\})=x</math> oraz dla dowolnego <math>\alpha\subseteq \mathcal{P} X</math> | Algebrą dla tej monady jest każda para <math>(\mathcal{P} X,h\colon \mathcal{P} X\to X)</math>, która spełnia: <math>h(\{ x\})=x</math> oraz dla dowolnego <math>\alpha\subseteq \mathcal{P} X</math>: | ||
<center><math>h(\{h(A)\mid A\in \alpha\})= h(\bigcup\alpha).</math></center> | <center><math>h(\{h(A)\mid A\in \alpha\})= h(\bigcup\alpha).</math></center> | ||
Mając strukturę algebry na <math>X</math> możemy teraz zdefiniować częściowy porządek na <math>X</math> jako: | Mając strukturę algebry na <math>X</math>, możemy teraz zdefiniować częściowy porządek na <math>X</math> jako: | ||
<center><math>x\leq y \iff h(\{x,y\})=y.</math></center> | <center><math>x\leq y \iff h(\{x,y\})=y.</math></center> | ||
| Linia 214: | Linia 213: | ||
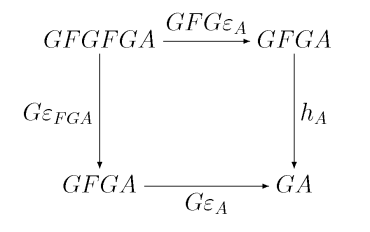
co daje <math>h_{FX} = G\varepsilon_{FX}</math>. Widzimy więc, jak strzałka <math>h</math> jest zdefiniowana na obrazie <math>F</math>. A jak jest w ogólnym przypadku? | co daje <math>h_{FX} = G\varepsilon_{FX}</math>. Widzimy więc, jak strzałka <math>h</math> jest zdefiniowana na obrazie <math>F</math>. A jak jest w ogólnym przypadku? | ||
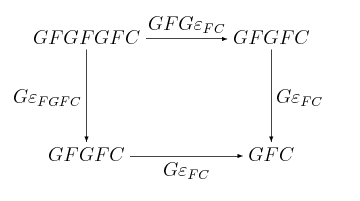
Niech <math>A\in \mathbf{D}_0</math>. Skoro <math>\varepsilon_A\colon FGA\to A</math> jest strzałką w <math>\mathbf{D}</math>, to strzałka <math>K(\varepsilon_A)\colon K(FGA)\to K(A)</math> jest z definicji funktora <math>K</math> morfizmem <math>\mathbb{T}</math>-algebr nad <math>\mathbf{C}</math>. Dokładnie mówiąc, jest to morfizm pomiędzy algebrą <math>K(FGA)=(GFGA,h_{FGA}=G\varepsilon_{FGA})</math> | Niech <math>A\in \mathbf{D}_0</math>. Skoro <math>\varepsilon_A\colon FGA\to A</math> jest strzałką w <math>\mathbf{D}</math>, to strzałka <math>K(\varepsilon_A)\colon K(FGA)\to K(A)</math> jest z definicji funktora <math>K</math> morfizmem <math>\mathbb{T}</math>-algebr nad <math>\mathbf{C}</math>. Dokładnie mówiąc, jest to morfizm pomiędzy algebrą <math>K(FGA)=(GFGA,h_{FGA}=G\varepsilon_{FGA})</math> a algebrą <math>(GA,h_A)</math>. To znaczy, że poniższy diagram komutuje: | ||
<center>[[Grafika:tk-11.16.png]]</center> | <center>[[Grafika:tk-11.16.png]]</center> | ||
Używając faktu, że <math>\varepsilon</math> jest kojednością sprzężenia, zgodnie z [[Teoria_kategorii_dla_informatyków/Wykład_9:_Sprzężenia_I#mod9:thm:adjtriangle|Twierdzeniem 9.3]] dostajemy | Używając faktu, że <math>\varepsilon</math> jest kojednością sprzężenia, zgodnie z [[Teoria_kategorii_dla_informatyków/Wykład_9:_Sprzężenia_I#mod9:thm:adjtriangle|Twierdzeniem 9.3]], dostajemy: | ||
<center><math>h_A = h_A\circ 1_{GFGA} = h_A\circ GFG\varepsilon_A\circ GF\eta_{GA} = G\varepsilon_A\circ G\varepsilon_{FGA}\circ GF\eta_{GA} = G\varepsilon_A\circ 1_{GA}= G\varepsilon_A.</math></center> | <center><math>h_A = h_A\circ 1_{GFGA} = h_A\circ GFG\varepsilon_A\circ GF\eta_{GA} = G\varepsilon_A\circ G\varepsilon_{FGA}\circ GF\eta_{GA} = G\varepsilon_A\circ 1_{GA}= G\varepsilon_A.</math></center> | ||
A zatem, jeśli <math>K</math> istnieje, to musimy mieć | A zatem, jeśli <math>K</math> istnieje, to musimy mieć: | ||
<center><math>K(f\colon A\to B)=(GA,G\varepsilon_A)\stackrel{Gf}{\to}(GB,G\varepsilon_B).</math></center> | <center><math>K(f\colon A\to B)=(GA,G\varepsilon_A)\stackrel{Gf}{\to}(GB,G\varepsilon_B).</math></center> | ||
Łatwo sprawdzić, że ten przepis rzeczywiście definiuje funktor <math>K</math>, który spełnia zarówno równość <math>KF=F^{\mathbb{T}}</math>, jak i <math>G^{\mathbb{T}}K=G</math>. Gdyby istniały dwa takie funktory <math>K_1,K_2</math>, to skoro <math>G^{\mathbb{T}}K_1 = G = G^{\mathbb{T}}K_2</math>, wierność <math>G^{\mathbb{T}}</math> implikuje <math>K_1=K_2</math>, co kończy dowód. </div></div> | Łatwo sprawdzić, że ten przepis rzeczywiście definiuje funktor <math>K</math>, który spełnia zarówno równość <math>KF=F^{\mathbb{T}}</math>, jak i <math>G^{\mathbb{T}}K=G</math>. Gdyby istniały dwa takie funktory <math>K_1,K_2</math>, to skoro <math>G^{\mathbb{T}}K_1 = G = G^{\mathbb{T}}K_2</math>, wierność <math>G^{\mathbb{T}}</math> implikuje <math>K_1=K_2</math>, co kończy dowód. </div></div> | ||
Wersja z 12:22, 27 lis 2006
==Zadanie 11.1==
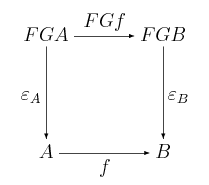
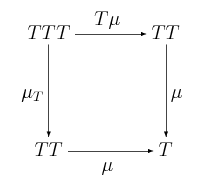
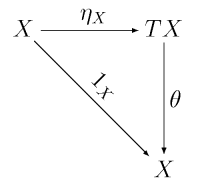
Udowodnij, że jeśli oraz , to naturalność implikuje, że poniższy diagram:
komutuje.
==Zadanie 11.2==
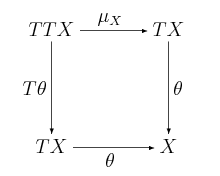
Niech będzie monadą nad . Pokaż że dla dowolnego , para jest -algebrą.
==Zadanie 11.3==
Udowodnij Twierdzenie 11.2.
==Zadanie 11.4==
Niech będzie monadą nad posetem . Pokaż, od jakiego sprzężenia pochodzi ta monada.
==Zadanie 11.5==
Udowodnij, że jest monadą nad dla kowariantnego funktora potęgowego .
==Zadanie 11.6==
Niech będzie monoidem. Udowodnij, że funktor
wraz z transformacjami naturalnymi oraz definiuje monadę , której -algebrami są -automaty.
==Zadanie 11.7==
Udowodnij, że funktor , który dodaje do posetu nowy element najmniejszy wraz z funktorem zapominania indukuje monadę nad . Jakie są algebry dla tej monady?
==Zadanie 11.8==
Wykaż, że algebrami dla monady nad indukowanej przez kowariantny funktor potęgowy są półkraty zupełne i homomorfizmy tych półkrat (tzn. funkcje zachowujące dowolne suprema).
==Zadanie 11.9==
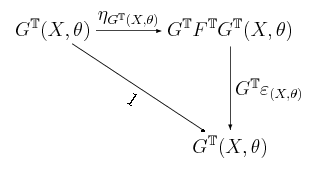
Wykaż, że sprzężenie , od którego pochodzi monada jest obiektem końcowym pewnej kategorii, w następującym sensie: jeśli dla jest sprzężeniem, które indukuje , to istnieje dokładnie jeden funktor taki, że dwa poniższe diagramy komutują:
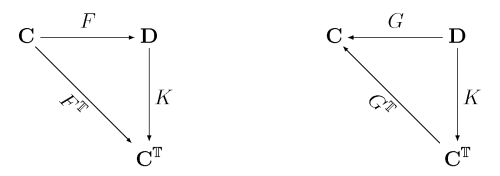
Taki funktor nazywa się funktorem porównawczym (ang. comparison functor) dla sprzężenia .