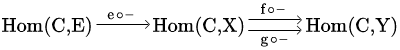Teoria kategorii dla informatyków/Ćwiczenia 8: Diagramy, granice i kogranice

Na początku zobaczmy, że istnienie granic da się w pełni wyrazić w języku funktorów reprezentowalnych.

==Zadanie 8.1==

Niech $\mathbf{𝐉}$ będzie kategorią, $\mathbf{𝐂}$ - kategorią lokalnie małą, $D:\mathbf{𝐉}\to \mathbf{𝐂}$ diagramem. Udowodnić, że $D$ ma granicę $(X,c)$ wtedy i tylko wtedy, gdy funktor $\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(-,D):{\mathbf{𝐂}}^{op}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ jest reprezentowalny.

Funktor ten definiujemy następująco:

$\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(-,D)(X):=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(X,D)$ (zbiór stożków o wierzchołku $X$), $\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(-,D)(f:X\to Y):=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(f,D):\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(Y,D)\to \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(X,D)$ $(Y,d_j)\mapsto (X,d_j\circ f)$

Rozwiązanie:

Sprawdźmy, co to znaczy, że $\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(-,D)$ jest reprezentowalny. Zgodnie z charakterystyką reprezentowalności -Lemat 7.5 - dzieje się tak, gdy istnieje stożek $(X,c)\in \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(X,D)$ taki, że dla dowolnego innego stożka $(Y,d)$ nad $D$ istnieje dokładnie jedna strzałka $f:Y\to X$ w $\mathbf{𝐂}$ taka, że:

$\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}(f,D)((X,c))=(Y,d)$

Ale przecież ten warunek jest równoważny stwierdzeniu, że $d_j=c_j\circ f$ dla każdego $j\in {\mathbf{𝐉}}_0$. Co należało wykazać.

==Zadanie 8.2==

Udowodnij następujące twierdzenie Petera Freyda: Jeśli mała kategoria jest zupełna, to jest preporządkiem.

Wskazówka:

Przypuśćmy, że tak nie jest i weźmy $A,B\in {\mathbf{𝐂}}_0$ takie, że $\mathrm{H}\mathrm{o}\mathrm{m}(A,B)\ge 2$. Rozważmy moc zbioru $\mathrm{H}\mathrm{o}\mathrm{m}(A,{\mathrm{\Pi }}_{i\in I}B)$ dla $I={\mathbf{𝐂}}_1$.

Rozwiązanie:

Postępujemy zgodnie ze Wskazówką. Z jednej strony mamy:

$|{\mathbf{𝐂}}_1|\ge |\mathrm{H}\mathrm{o}\mathrm{m}(A,{\mathrm{\Pi }}_{i\in I}B)|$

zaś z drugiej strony, ze względu na izomorfizm:

$\mathrm{H}\mathrm{o}\mathrm{m}(A,{\mathrm{\Pi }}_{i\in I}B)\cong {\mathrm{\Pi }}_{i\in I}\mathrm{H}\mathrm{o}\mathrm{m}(A,B)\cong \mathrm{H}\mathrm{o}\mathrm{m}(A,B{)}^J$

mamy:

$|\mathrm{H}\mathrm{o}\mathrm{m}(A,{\mathrm{\Pi }}_{i\in I}B)|=|\mathrm{H}\mathrm{o}\mathrm{m}(A,B){|}^{|J|}\ge |{𝒫}(J)|$

co daje sprzeczność z twierdzeniem Cantora z teorii mnogości.

==Zadanie 8.3==

Niech $\mathbf{𝐂}$ będzie kategorią, w której istnieją wszystkie granice typu $\mathbf{𝐉}$. Udowodnij, że $\underset{\leftarrow \mathbf{𝐉}}{\lim }$ jest funktorem typu $[\mathbf{𝐉},\mathbf{𝐂}]\to \mathbf{𝐂}$.

Wskazówka:

Oczywiście działanie $\underset{\leftarrow \mathbf{𝐉}}{\lim }$ na obiektach jest następujące: $D\mapsto \underset{\leftarrow \mathbf{𝐉}}{\lim }(D)$, gdzie

$\{c_j^D:\underset{\leftarrow \mathbf{𝐉}}{\lim }D\to D(j)\mid j\in {\mathbf{𝐉}}_0\}$

jest stożkiem granicznym. Dla dowolnego przekształcenia diagramów $\delta :D\to D^{\prime }$ kolekcja

$\{\underset{\mathbf{𝐉}}{\lim }D\stackrel{c_j^D}{\to }D(j)\stackrel{{\delta }_j}{\to }{D}^{\prime }(j)\mid j\in {\mathbf{𝐉}}_0\}$

jest stożkiem granicznym nad $D^{\prime }$ (tj. granicą $D^{\prime }$). Z warunku uniwersalnego istnieje więc dokładnie jedna strzałka, oznaczmy ją $\underset{\leftarrow \mathbf{𝐉}}{\lim }\delta :\underset{\leftarrow \mathbf{𝐉}}{\lim }(D)\to \underset{\leftarrow \mathbf{𝐉}}{\lim }(D^{\prime })$, która sprawia, że poniższy diagram komutuje:

Rozwiązanie:

To, że $\underset{\leftarrow \mathbf{𝐉}}{\lim }$ jest funktorem wynika wprost z własności uniwersalnej diagramu we Wskazówce. Na przykład, dla złożenia:

$D\stackrel{\delta }{\to }{D}^{\prime }\stackrel{{\delta }^{\prime }}{\to }{D}^{″}$

obie strzałki $\underset{\leftarrow \mathbf{𝐉}}{\lim }({\delta }^{\prime }\circ \delta )$ oraz $\underset{\leftarrow \mathbf{𝐉}}{\lim }{\delta }^{\prime }\circ \underset{\leftarrow \mathbf{𝐉}}{\lim }\delta$ są faktoryzacjami diagramu:

$\{\delta {\text{'}}_j\circ \delta \circ c_j^D\mid j\in {\mathbf{𝐉}}_0\}$

a co za tym idzie - są równe. Zachowywanie identyczności wynika od razu z faktu, że dla dowolnej granicy

$\{c_j^D:\underset{\leftarrow \mathbf{𝐉}}{\lim }D\to D(j)\mid j\in {\mathbf{𝐉}}_0\}$ zarówno identyczność na $\underset{\leftarrow \mathbf{𝐉}}{\lim }D$, jak i $\underset{\leftarrow \mathbf{𝐉}}{\lim }\delta$ dla $\delta =1_D:D\to D$ są faktoryzacjami diagramu $D$, a zatem muszą być równe.

Uwaga

Mówimy, że funktor $F:\mathbf{𝐂}\to \mathbf{𝐃}$ zachowuje granice typu $\mathbf{𝐉}$, jeśli z faktu, że $c_j:L\to D_j$ jest granicą diagramu $D:\mathbf{𝐉}\to \mathbf{𝐂}$ wynika, że stożek $F{c}_j:FL\to F{D}_j$ jest granicą diagramu $F\circ D:\mathbf{𝐉}\to \mathbf{𝐃}$. W skrócie można to zapisać tak: $F(\underset{\leftarrow \mathbf{𝐉}}{\lim }{D}_j)\cong \underset{\leftarrow \mathbf{𝐉}}{\lim }F(D_j)$

Funktor zachowujący wszystkie granice nazywa się ciągłym.

==Zadanie 8.4==

Udowodnić, że hom-funktory są ciągłe.

Wskazówka:

Niech $\mathbf{𝐉}$ będzie małą kategorią. Pokażemy, że hom-funktory: $\mathrm{H}\mathrm{o}\mathrm{m}(C,-):\mathbf{𝐂}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ dla $C\in {\mathbf{𝐂}}_0$ zachowują ekwalizatory i wszystkie produkty mocy mniejszej lub równej mocy $\mathbf{𝐉}$, a potem użyjemy Twierdzenia 8.3. Gwoli wyjaśnienia, produkt o mocy $0$ jest po prostu obiektem końcowym (nieprawdaż?).

Rozwiązanie:

Po pierwsze, załóżmy, że $\mathbf{𝐂}$ ma obiekt końcowy $\mathbf{𝟏}$ i zauważmy, że $\mathrm{H}\mathrm{o}\mathrm{m}(C,\mathbf{𝟏})=\{C\}\cong {\mathbf{𝟏}}_{\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}}$ (bo wszystkie singletony są izomorficzne w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$). Po drugie, wiemy już z Zadania 3.5, że hom-funktory zachowują produkty binarne. Podobnie da się pokazać, że hom-funktory zachowują produkty dowolnej mocy. Oto argument: dla dowolnego produktu ${\mathrm{\Pi }}_{i\in I}{Z}_i$ wraz z projekcjami ${\mathrm{\Pi }}_{i\in I}{Z}_i\to Z_i$ każda strzałka $f:C\to {\mathrm{\Pi }}_{i\in I}{Z}_i$ rozkłada się na strzałki $f_i:=p_i\circ f$. Odwrotnie, dla rodziny strzałek $\{f_i:C\to Z_i\mid i\in I\}$, gdzie $f_i:C\to Z_i$, z własności uniwersalnej produktu, istnieje dokładnie jedna strzałka $(f_i):C\to {\mathrm{\Pi }}_{i\in I}{Z}_i$ taka, że $f_i=p_i\circ f$. Jest więc oczywiste, że odwzorowanie:

$f:X\to {\mathrm{\Pi }}_{i\in I}{Z}_i\mapsto p_i\circ f$

jest szukanym izomorfizmem z odwrotnością:

$\{f_i:Z\to X_i\mid i\in I\}\mapsto (f_i)$

To znaczy, że:

$\mathrm{H}\mathrm{o}\mathrm{m}(C,{\mathrm{\Pi }}_i{Z}_i)\cong {\mathrm{\Pi }}_i\mathrm{H}\mathrm{o}\mathrm{m}(C,Z_i)$

W końcu, po trzecie, jeśli

jest ekwalizatorem, to rozważmy diagram:

Musimy pokazać, że jest to ekwalizator w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$. Rzeczywiście, dla dowolnej strzałki $h:C\to E$ takiej, że $(f\circ -)h=(g\circ -)h$ mamy $f\circ h=g\circ h$. Ponieważ $E$ jest ekwalizatorem, istnieje dokładnie jedna strzałka $k:C\to E$ taka, że $e\circ k=h$. Innymi słowy, to znaczy, że mamy dokładnie jedną strzałkę $k$ taką, że $(e\circ -)(k)=h$. To znaczy, że:

$(e\circ -):\mathrm{H}\mathrm{o}\mathrm{m}(C,E)\to \mathrm{H}\mathrm{o}\mathrm{m}(C,X)$ jest ekwalizatorem $(f\circ -)$ i $(g\circ -)$. Pokazaliśmy, że założenia Twierdzenia 8.3 są spełnione, a zatem hom-funktor zachowuje dowolne granice, tj. jest ciągły.

==Zadanie 8.5==

Pokażmy, że dla lokalnie małej kategorii $\mathbf{𝐂}$, funktor ewaluacji

${\mathrm{e}\mathrm{v}}_{{\mathbf{𝐂}}^{op}}:[{\mathbf{𝐂}}^{op},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]\times {\mathbf{𝐂}}^{op}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$

znany z Wykładu 7. i Zadania 7.1 jest ciągły.

Rozwiązanie:

Niech $\mathbf{𝐉}$ będzie małą kategorią. Niech $F:\mathbf{𝐉}\to [{\mathbf{𝐂}}^{op},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]$ będzie diagramem w $[{\mathbf{𝐂}}^{op},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]$. Wówczas jego granica, jeśli istnieje, jest obiektem $[{\mathbf{𝐂}}^{op},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]$, czyli funktorem $(\underset{\leftarrow j}{\lim }{F}_j)\in [{\mathbf{𝐂}}^{op},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]$ Zgodnie z lematem Yonedy, dla każdego obiektu $X\in {\mathbf{𝐂}}_0$, istnieje naturalny izomorfizm:

$(\underset{\leftarrow j}{\lim }{F}_j)(X)\cong \mathrm{H}\mathrm{o}\mathrm{m}({𝒴}(X),\underset{\leftarrow j}{\lim }{F}_j)$

Ale hom-funktory są ciągłe, Zadanie 8.4,więc używając po kolei: tego faktu i lematu Yonedy raz jeszcze, dostajemy:

$\mathrm{H}\mathrm{o}\mathrm{m}({𝒴}(X),\underset{\leftarrow j}{\lim }{F}_j)\cong \underset{\leftarrow j}{\lim }\mathrm{H}\mathrm{o}\mathrm{m}({𝒴}(X),F_j)\cong \underset{\leftarrow j}{\lim }{F}_j(X)$ Ta równość jest właśnie dowodem na to, że ewaluacja zachowuje granice.

==Zadanie 8.6==

Udowodnij, że funktor Yonedy ${𝒴}:\mathbf{𝐂}\to [{\mathbf{𝐂}}^{op},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]$ jest ciągły.

Wskazówka:

Ponieważ granice w kategoriach funktorów są liczone po współrzędnych, mając dany diagram $D:\mathbf{𝐉}\to \mathbf{𝐂}$ wraz z granicą

$L=\{c_j:L\to D(j)\mid j\in {\mathbf{𝐉}}_0\}$

wystarczy pokazać, że dla dowolnego $X\in {\mathbf{𝐂}}_0$

$\{(c_j\circ -):{\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(X,L)\to {\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(X,D(j))\}$

jest stożkiem granicznym dla diagramu

${\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(X,D(-))={𝒴}(D(-))(X):\mathbf{𝐉}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$

Rozwiązanie:

Niech zatem:

$\{d_j:S\to {\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(X,D(j))\mid j\in {\mathbf{𝐉}}_0\}$

będzie dowolnym innym stożkiem nad ${\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(X,D(-))$. Wówczas dla każdego $s\in S$

$\{d_j(s):X\to D(j))\mid j\in {\mathbf{𝐉}}_0\}$

jest stożkiem nad $D$, więc istnieje dokładnie jedna strzałka $f(s):X\to L$ taka, że $c_j\circ f(s)=d_j(s)$ dla każdego $j\in {\mathbf{𝐉}}_0$. A zatem strzałka $s\mapsto f(s)$ jest jedyną typu $S\to {\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(X,L)$ taką, że $(c_j\circ -)\circ f=d_j$, co należało pokazać.

Uwaga dla dociekliwych

Funktor Yonedy zwykle nie zachowuje kogranic. Na przykład ${𝒴}:{\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}}_{fin}\to [{\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}}_{fin}^{op},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]$ nie zachowuje obiektu początkowego $\mathrm{\varnothing }$.

==Zadanie 8.7==

Pokaż, że hom-funktor ${\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(-,X):{\mathbf{𝐂}}^{op}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ jest ciągły, tj.

${\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(\underset{\leftarrow j}{\lim }{Z}_j,X)\cong \underset{\to j}{\lim }{\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(Z_j,X)$

Wskazówka:

Zadanie można zrobić łatwo na trzy sposoby.

Rozwiązanie:

Sposób pierwszy: przez szczegółowy dowód dualny do Zadania 8.4. Sposób drugi: przez odwołanie się do zasady dualności względem Zadania 8.4 (czyli sposób pierwszy dla leniwych...). Sposób trzeci: wykorzystując Zadania 8.5, 8.6. Oto ten sposób: dowód dualny do tego w Zadaniu 8.6 pokazuje, że dualny funktor Yonedy ${{𝒴}}^{op}:{\mathbf{𝐂}}^{op}\to [\mathbf{𝐂},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]$ zmienia granice na kogranice. Dowód identyczny do tego w Zadaniu 8.5 pokazuje, że funktor ewaluacji $\mathrm{e}\mathrm{v}:[\mathbf{𝐂},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]\times \mathbf{𝐂}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ jest ciągły, a zatem złożenie:

$\mathrm{H}\mathrm{o}\mathrm{m}(-,X)=\mathbf{𝐂}\stackrel{{{𝒴}}^{op}}{\to }[{\mathbf{𝐂}}^{op},\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}]\stackrel{\mathrm{e}\mathrm{v}}{\to }\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ jest funktorem ciągłym (tzn. ze względu na kontrawariantność zamienia granice na kogranice).