Teoria kategorii dla informatyków/Ćwiczenia 2: Morfizmy specjalne

==Zadanie 2.1==

Udowodnij, że jeśli $\mathbf{𝟏}$ jest obiektem końcowym w kategorii $\mathbf{𝐂}$, to każdy morfizm, którego dziedziną jest $\mathbf{𝟏}$, jest sekcją.

Wskazówka:

Wykorzystujemy własność uniwersalną $\mathbf{𝟏}$.

Rozwiązanie:

Niech $A\in {\mathbf{𝐂}}_0$ i $\mathbf{𝟏}\stackrel{s}{\to }A$. Obiekt $\mathbf{𝟏}$ jest końcowy, więc istnieje jedyna strzałka typu $A\to \mathbf{𝟏}$, a stary zwyczaj nakazuje nazwać tę strzałkę po prostu $A$. Z faktu, że $\mathbf{𝟏}$ jest końcowy, wynika również, że złożenie $A\circ s$ jest jedną jedyną strzałką o dziedzinie i kodziedzinie $\mathbf{𝟏}$. To złożenie musi być więc równe identyczności na $\mathbf{𝟏}$. Tak jest: $A\circ s=1_{\mathbf{𝟏}}$. Pokazaliśmy w ten sposób, że $s$ jest sekcją, znaleźliśmy bowiem lewą odwrotność $A$ do $s$.

==Zadanie 2.2==

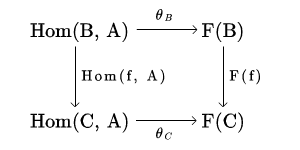
Udowodnij Fakt 2.5.

Wskazówka:

Aby efektywnie rozwiązywać zadania tego typu, warto nie podawać wielu szczegółów, które zaciemniają obraz: np. nazwy dziedzin i kodziedzin istniejących morfizmów nie grają roli w rozwiązaniu. Zakładamy więc od tej pory milcząco, że jeśli w rozwiązaniu składamy morfizmy, to jest to a priori możliwe.

Rozwiązanie:

1. Chcemy wykazać, że jeśli $g\circ f$ jest mono, to $f$ jest mono. Trzeba pokazać, że $f$ skraca się z prawej strony. Niech więc $f\circ h=f\circ k$. Wtedy $g\circ f\circ h=g\circ f\circ k$. Z założenia, $g\circ f$ jest mono, czyli da się skrócić z prawej strony, co daje $h=k$, co należało pokazać.
2. Pokażmy, że złożenie monomorfizmów jest monomorfizmem. Niech $f,g$ będą mono. Załóżmy $g\circ f\circ h=g\circ f\circ k$ dla pewnych morfizmów $h,k$. Wtedy z monomorficzności $g$ otrzymujemy $f\circ h=f\circ k$. Monomorficzność $f$ daje zatem $h=k$, co należało pokazać.
3. Dowód faktu, że jeśli $g\circ f$ jest epi, to $g$ jest epi, jest dualny do dowodu własności (1). To kończy dowód. (Niewprawnym czytelnikom należy się wyjaśnienie: jeśli $g\circ f$ jest epi w $\mathbf{𝐂}$, to $f\circ g$ jest mono w ${\mathbf{𝐂}}^{op}$. Własność (1) udowodniona powyżej implikuje, że $g$ jest mono w ${\mathbf{𝐂}}^{op}$, a Fakt 2.4 implikuje, że $g$ jest epi w $\mathbf{𝐂}$. Dualność jest szerzej omówiona na początku Wykładu 3.).
4. Pokażmy, że w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$, $f$ jest epi wtedy i tylko wtedy, gdy $f$ jest surjekcją. Załóżmy najpierw, że $f:A\to B$ jest surjekcją. Weźmy $g,h:B\to C$ takie, że $g\circ f=h\circ f$. Ale dowolny $b\in B$ jest postaci $f(a)=b$ dla $a\in A$. A zatem $h(b)=h(f(a))=g(f(a))=g(b)$. Funkcje $h$ i $g$ są równe na wszystkich elementach $b\in B$, czyli $g=h$. Wniosek: $f$ jest epi. Załóżmy teraz, że $f$ nie jest surjekcją. Wtedy istnieje $b_0\in B$, który nie jest obrazem przez funkcję $f$ żadnego elementu ze zbioru $A$. Weźmy $C:=\{0,1\}$ i funkcje $h,k:B\to C$ jak następuje: $h(b):=1$ dla każdego $b\in B$; $k(b_0):=0$ i $k(b):=1$ dla $b\ne b_0$. Przy takich definicjach mamy $h\circ f=k\circ f$, ale $h\ne k$. To dowodzi, że $f$ nie jest epimorfizmem.
5. Dowód faktu, że złożenie epimorfizmów jest epimorfizmem jest dualny do własności (2) powyżej.

==Zadanie 2.3==

Udowodnij Fakt 2.9.

Rozwiązanie:

1. Jeśli $g\circ f$ jest sekcją, to $f$ jest sekcją. Rzeczywiście, skoro $g\circ f$ jest sekcją, to ma lewą odwrotność $h$, tzn. istnieje $h$ takie, że $h\circ g\circ f=1$. Wtedy $h\circ g$ jest lewą odwrotnością $f$.
2. Złożenie sekcji jest sekcją. To prawda: niech $f,g$ będą składalnymi sekcjami z lewymi odwrotnościami odpowiednio $f^{\prime }$ i $g^{\prime }$. Rozważamy $f\circ g$. Wtedy $g^{\prime }\circ f^{\prime }$ jest poprawnie zdefiniowane i $g^{\prime }\circ f^{\prime }\circ f\circ g=g^{\prime }\circ (f^{\prime }\circ f)\circ g=g^{\prime }\circ 1\circ g=g^{\prime }\circ g=1$, co należało pokazać.
3. Pokażemy, że każdy funktor zachowuje sekcje. Niech $s$ będzie sekcją z lewą odwrotnością $s^{\prime }$, zaś $F$ funktorem. Wtedy z własności funktora wynika, że: $1_{F(\mathrm{d}\mathrm{o}\mathrm{m}(s))}=F(1_{\mathrm{d}\mathrm{o}\mathrm{m}(s)})=F(s^{\prime }\circ s)=F(s^{\prime })\circ F(s)$ a to oznacza, że $F(s)$ jest sekcją z lewą odwrotnością $F(s^{\prime })$.
4. Pokażemy, że każdy pełny i wierny funktor odzwierciedla sekcje. Niech $s:A\to B$ będzie morfizmem takim, że $F(s):F(A)\to F(B)$ jest sekcją. To znaczy (używamy tu również pełności $F$), iż istnieje $s^{\prime }:B\to A$ tak, że $F(s^{\prime })\circ F(s)=1_{F(A)}$. Ale z własności funktora wynika, że $F(s^{\prime }\circ s)=F(s^{\prime })\circ F(s)=1_{F(A)}=F(1_A)$. Wierność $F$ implikuje zatem $s^{\prime }\circ s=1_A$. To świadczy o tym, że $s$ jest sekcją.
5. Złożenie retrakcji jest retrakcją. Rzeczywiście: jeśli $f,g$ są składalnymi retrakcjami w $\mathbf{𝐂}$, to $g,f$ są składalnymi sekcjami w ${\mathbf{𝐂}}^{op}$. Dalszy ciąg dowodu wynika natychmiast z (2) powyżej i dualności sekcji i retrakcji.
6. Jeśli $g\circ f$ jest retrakcją, to $g$ jest retrakcją. Dowód dualny do (1) powyżej.
7. Każdy funktor zachowuje retrakcje. Dowód dualny do (3) powyżej: dostajemy go za darmo!
8. Każdy pełny i wierny funktor odzwierciedla retrakcje - dowód dualny do (4) powyżej - znów za darmo!
9. Morfizm $f$ jest izomorfizmem wtedy i tylko wtedy, gdy jest sekcją i retrakcją jednocześnie: jest oczywiste, że jeśli $f$ jest izomorfizmem, to ma lewą i prawą odwrotność. Jeśli zaś $f$ jest sekcją i retrakcją, to istnieją dwa morfizmy $g,h$ takie, że $g\circ f=1_{\mathrm{d}\mathrm{o}\mathrm{m}(f)}$ i $f\circ h=1_{\mathrm{c}\mathrm{o}\mathrm{d}(f)}$. Wtedy $g=g\circ 1_{\mathrm{c}\mathrm{o}\mathrm{d}(f)}=g\circ f\circ h=1_{\mathrm{d}\mathrm{o}\mathrm{m}(f)}\circ h=h$. Strzałka $h$, będąc lewą i prawą odwrotnością $f$, świadczy o tym, że $f$ jest izomorfizmem.
10. Każdy pełny i wierny funktor odzwierciedla izomorfizmy. Rzeczywiście, jak pokazaliśmy powyżej, taki funktor odzwierciedla sekcje i retrakcje, czyli odzwierciedla izomorfizm na izomorfizm.

==Zadanie 2.4==

Wykaż, że zrozumienie relacji pomiędzy sekcjami i monomorfizmami oraz retrakcjami i epimorfizmami zawsze da się jeszcze trochę utrudnić, tzn. udowodnij, że:

1. morfizm $f$ jest izomorfizmem wtedy i tylko wtedy, gdy jest retrakcją i monomorfizmem;
2. morfizm $f$ jest izomorfizmem wtedy i tylko wtedy, gdy jest sekcją i epimorfizmem;
3. każdy wierny funktor odzwierciedla monomorfizmy i epimorfizmy;
4. każdy funktor reprezentowalny zachowuje monomorfizmy.

Wskazówka:

Jedynym zadaniem nietrywialnym jest ostatnie, gdzie należy najpierw udowodnić tezę dla hom-funktora $\mathrm{H}\mathrm{o}\mathrm{m}(-,A):{\mathbf{𝐂}}^{op}\to \mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$, $A\in {\mathbf{𝐂}}_0$ - patrz Przykład 5.7.

Rozwiązanie:

(1) W świetle tego co wiemy do tej pory, wystarczy pokazać, że monomorficzna retrakcja $f$ jest izomorfizmem. Skoro $f$ jest retrakcją, to dla pewnej strzałki $g$ mamy $f\circ g=1$. Więc $f\circ g\circ f=f$. Ale z monomorficzności $f$ wynika, że możemy w ostatnim równaniu skrócić $f$ z lewej strony, czyli $g\circ f=1$. To znaczy, że $f$ jest izomorfizmem z odwrotnością $g$. (2) jest zdaniem dualnym do (1), a więc dowód mamy za darmo. (3) Niech $f$ będzie taką strzałką, że $F(f)$ jest mono. Załóżmy, że $f\circ g=f\circ h$. Funktory zachowują złożenia, co daje $F(f)\circ F(g)=F(f)\circ F(h)$. Z założenia, $F(g)=F(h)$, a z wierności: $g=h$, co należało pokazać. Dowód dla epimorfizmu jest dualny. (4) Niech $f:C\to B\in {\mathbf{𝐂}}_1$ będzie mono. Przypuśćmy, że $\mathrm{H}\mathrm{o}\mathrm{m}(f,A)\circ g=\mathrm{H}\mathrm{o}\mathrm{m}(f,A)\circ h$ dla pewnych strzałek $g,h:Z\to \mathrm{H}\mathrm{o}\mathrm{m}(B,A)$, gdzie $Z\in {\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}}_0$ (Zwróćmy uwagę, że kontrawariantność funktora implikuje, że $\mathrm{H}\mathrm{o}\mathrm{m}(f,A):\mathrm{H}\mathrm{o}\mathrm{m}(B,A)\to \mathrm{H}\mathrm{o}\mathrm{m}(C,A)$.) To znaczy, że dla dowolnego $z\in Z$ mamy $\mathrm{H}\mathrm{o}\mathrm{m}(f,A)(g(z))=\mathrm{H}\mathrm{o}\mathrm{m}(f,A)(h(z))$, czyli $f\circ g(z)=f\circ h(z)$. Ale $f$ jest mono; stąd $g(z)=h(z)$ dla każdego $z\in Z$. W $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ ta równość oznacza, że $g=h$, co pokazuje, że hom-funktory odzwierciedlają monomorfizmy. Jeśli teraz $F$ jest reprezentowalny, tzn. $\theta :F\cong \mathrm{H}\mathrm{o}\mathrm{m}(-,A)$ dla pewnego $A\in {\mathbf{𝐂}}_0$ - porównaj z Definicją 7.4 - to istnieją dwie bijekcje w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ - mianowicie ${\theta }_B$ i ${\theta }_C$ takie, że poniższy diagram komutuje:

Załóżmy zatem, że $F(f)\circ g=F(f)\circ h$ dla pewnych strzałek $g,h:Z\to F(B)$. Patrząc na diagram powyżej, widzimy, że $F(f)={\theta }_C\circ \mathrm{H}\mathrm{o}\mathrm{m}(f,A)\circ {\theta }_B^{-1}$, i każda z tych trzech strzałek jest mono (obie $\theta$-ty są bijekcjami - czyli injekcjami w szczególności). A zatem $g=h$. Wykazaliśmy, że $F(f)$ jest monomorfizmem, q.e.d.

==Zadanie 2.5==

Udowodnij, że w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ zdanie każdy epimorfizm jest retrakcją, jest równoważny pewnikowi wyboru.

Wskazówka:

Aksjomat wyboru (pewnik wyboru) w teorii mnogości to zdanie: Dla każdej rodziny $\{A_i\},i\in I$ złożonej z niepustych, parami rozłącznych zbiorów, istnieje funkcja $f:I\to \bigcup _{i\in I}{A}_i$, która ma własność $f(i)\in A_i$ dla każdego $i\in I$.

Rozwiązanie:

Załóżmy najpierw, że każdy epimorfizm jest retrakcją. Niech $\{A_i\}$ będzie dowolną rodziną niepustych, parami rozłącznych zbiorów.

Konstruujemy epimorfizm (surjekcję) $e:\bigcup _{i\in I}{A}_i\to I$ jako $A_i\ni a\mapsto i$. Skoro $e$ jest retrakcją, to ma prawą odwrotność: istnieje funkcja $f:I\to \bigcup A_i$ taka, że $e\circ f=1_I$. Ostatnie równanie oznacza, że $e(f(i))=i$, co jest równoważne informacji, że $f(i)\in A_i$. Odwrotnie, załóżmy pewnik wyboru. Niech $e:A\to B$ będzie dowolnym epimorfizmem (surjekcją). Rozważmy rodzinę $A_b:=\{e^{-1}[\{b\}]\mid b\in B\}$.

Ta rodzina jest parami rozłączna i niepusta, bo $e$ jest funkcją. Ponadto $\bigcup _{b\in B}{A}_b=A$. Pewnik wyboru mówi więc, że istnieje funkcja $f:B\to A$, która ma własność $f(b)\in A_b$. Innymi słowy, $f(b)\in e^{-1}[\{b\}]$, co oznacza $e(f(b))=b$. albo $e\circ f=1_B$. Pokazaliśmy, że $f$ jest prawą odwrotnością $e$, co świadczy o tym, że $e$ jest retrakcją.

==Zadanie 2.6==

Udowodnij Twierdzenie 2.12, tzn. pokaż, że retrakt dziedziny ciągłej jest dziedziną ciągłą.

Rozwiązanie:

Pokażemy najpierw zupełność $S$. Niech $A$ będzie skierowanym podzbiorem $S$. Ponieważ $s$ jest funkcją monotoniczną, obraz $s[A]$ jest skierowanym podzbiorem dziedziny ciągłej $T$. A zatem posiada supremum $\bigvee {}^{\uparrow }s[A]$ i jasne jest, że element $r(\bigvee {}^{\uparrow }s[A])$ jest ograniczeniem górnym zbioru $A$ w $S$. Niech $u$ będzie dowolnym innym ograniczeniem górnym $A$, tzn. $A⊑u$. Wtedy $s[A]⊑s(u)$, czyli $\bigvee {}^{\uparrow }s[A]⊑s(u)$. Funkcja $r$ jest monotoniczna, a zatem $r(\bigvee {}^{\uparrow }s[A])⊑r(s(u))=u$. To dowodzi, że $r(\bigvee {}^{\uparrow }s[A])$ jest najmniejszym ograniczeniem górnym $A$, czyli jego supremum. Pokazaliśmy, że dowolny zbiór skierowany $A$ w $S$ ma supremum, czyli że $S$ jest posetem zupełnym. Zauważmy, że w tym dowodzie ciągłość funkcji nie została wykorzystana; przyda się nam natomiast w następnym paragrafie.

Niech $c\in B$ aproksymuje $s(x)$ dla $x\in S$. Pokażemy, że $r(x)\ll x$. Niech $A$ będzie skierowanym podzbiorem $S$, który posiada supremum $\bigvee {}^{\uparrow }A⊒x$. Z ciągłości $s$ wynika, że $\bigvee {}^{\uparrow }s[A]=s(\bigvee {}^{\uparrow }A)⊒s(x)$, a zatem dla pewnego $a\in A$ musimy mieć $s(a)⊒c$. To implikuje $a=r(s(a))⊒r(c)$, co dowodzi $r(x)\ll x$. Ciągłość $r$ implikuje, że $x$ jest supremum zbioru $r[\Downarrow s(x)\cap B]$, który jest skierowanym podzbiorem $\Downarrow x\cap r[B]$. Jak łatwo się przekonać, to znaczy, że $r[B]$ jest bazą dla $S$, czyli $S$ jest ciągły.

==Zadanie 2.7==

Udowodnij Twierdzenie 2.13, tzn. pokaż, że każda dziedzina ciągłą jest retraktem dziedziny algebraicznej.

Wskazówka:

Dla prostoty rozważań jako bazę wybieramy cały poset $P$. Należy najpierw wykazać następującą charakteryzację relacji aproksymacji w ${ℐ}(P,⊑)=({ℐ}(P),\subseteq )$: $I\ll J$ wtedy i tylko wtedy, gdy $(\mathrm{\exists }x\in J)I\subseteq \downarrow x$. To pozwoli nam stwierdzić, że ${ℐ}(P)$ jest dziedziną algebraiczną. Potem sprawdzamy, że $P$ jest retraktem ${ℐ}(P)$.

Rozwiązanie:

Para $({ℐ}(P),\subseteq )$ jest oczywiście częściowym porządkiem. Dla dowolnego $I\in {ℐ}(P)$ mamy:

$I=\bigcup \{\downarrow x\mid x\in I\}$

ponieważ $I$ jest dolny (suma jest skierowana, bo $I$ jest skierowany). Pokażemy, że w ${ℐ}(P)$ mamy:

$I\ll J⟺(\mathrm{\exists }x\in J)I\subseteq \downarrow x$

Załóżmy, że $I\ll J$. Skoro $J=\bigcup \{\downarrow a\mid \in J\}$, to istnieje $a\in J$ taki, że $I\subseteq \downarrow a$. Z drugiej strony załóżmy, że dla pewnych $I,J\in {ℐ}(P)$ oraz $x\in J$ zachodzi $I\subseteq \downarrow x$. Niech ${𝒟}$ będzie skierowanym podzbiorem ${ℐ}(P)$ takim, że $J\subseteq \bigcup {𝒟}$. Skoro $x\in J$, to istnieje $K\in {𝒟}$ taki, że $x\in K$, co implikuje $I\subseteq \downarrow x\subseteq K\in {𝒟}$. To dowodzi $I\ll J$.

Zauważmy, że z równoważności

$I\ll J⟺(\mathrm{\exists }x\in J)I\subseteq \downarrow x$

wynika, iż $\downarrow y\ll \downarrow y$ w ${ℐ}(P)$ dla dowolnego $y\in P$. A zatem na podstawie równości $I=\bigcup \{\downarrow x\mid x\in I\}$ łatwo wywnioskować, że $\{\downarrow x\mid x\in P\}$ jest bazą złożoną z elementów zwartych ${ℐ}(P)$. A zatem ${ℐ}(P)$ jest posetem algebraicznym. Jest to również dcpo, ponieważ dla dowolnej skierowanej rodziny ideałów ${ℰ}$ suma $\bigcup {ℰ}$ jest zbiorem skierowanym (patrz Zadanie 12.2) oraz dolnym (jako suma zbiorów dolnych), a zatem $\bigcup {}^{\downarrow }{ℰ}$ jest supremum ${ℰ}$ w ${ℐ}(P)$.

Przypomnijmy, jak wygląda nasza para sekcja-retrakcja: $s:P\to {ℐ}(P)$ dana jest jako $s(x):=\Downarrow x$ oraz $r:{ℐ}(P)\to P$ dana jako $r(I):=\bigvee {}^{\uparrow }I$. Funkcja $s$ jest monotoniczna, więc dla dowolnego zbioru skierowanego $D\subseteq P$ mamy $\bigvee {}^{\uparrow }s(d)\subseteq s(\bigvee {}^{\uparrow }D)$. Ale odwrotna inkluzja wynika z własności aproksymacji: jeśli $x\in s[\bigvee {}^{\uparrow }D]$, tzn. $x\ll \bigvee {}^{\uparrow }D$, to istnieje $d\in D$ taki, że $x\ll d$. Tym bardziej więc $x\in \bigvee {}^{\uparrow }s(d)$. Obie inkluzje dają równość $s(\bigvee {}^{\uparrow }D)=\bigvee {}^{\uparrow }s[D]$, czyli pokazują, że $s$ jest funkcją ciągłą w sensie Scotta. Ciągłość $r$ łatwo wynika z Zadania 12.2.

W końcu sprawdzamy dla dowolnego $x\in P$:

$(r\circ s)(x)=r(\Downarrow x)=\bigvee {}^{\uparrow }\Downarrow x=x$

ponieważ ostatnia równość jest stwierdzeniem ciągłości $P$. Wniosek: $r\circ s=1_P$, a zatem obie funkcje tworzą parę sekcja-retrakcja.

==Zadanie 2.8==

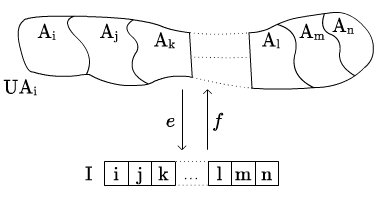
Udowodnij, że w parze e-p, funkcja $e:D\to E$ jest injekcją, zachowuje istniejące suprema i relację aproksymacji, zaś funkcja $p:E\to D$ jest surjekcją i zachowuje istniejące infima. Co więcej, pokaż, że funkcje $e$ i $p$ wzajemnie się wyznaczają, to znaczy, jeśli $e$ zanurzeniem w pewnej parze e-p, to projekcja $p$ może być wydefiniowana z $e$ jako $p(y)=\mathrm{m}\mathrm{a}\mathrm{x}{e}^{-1}[\downarrow y]$ dla $y\in E$ i vice versa: jeśli $p$ jest projekcją w parze e-p, to $e(x)=\mathrm{m}\mathrm{i}\mathrm{n}{p}^{-1}[\uparrow x]$ dla $x\in D$.

Wskazówka:

W parze e-p funkcja $e$ jest sekcją, zaś $p$ retrakcją, więc $e$ jest injekcją, zaś $p$ surjekcją.

Rozwiązanie:

Niech $S\subseteq D$ ma supremum $\bigvee S$. Oczywiście $e[S]⊑e(\bigvee S)$. Ale jeśli $e[S]⊑u$ dla pewnego $u$, to $S⊑p(u)$, więc $\bigvee S⊑p(u)$ i konsekwentnie $e(\bigvee S)⊑e(p(u))⊑u$. Wniosek: $e(\bigvee S)=\bigvee e[S]$. Dualnie, $p$ zachowuje istniejące infima.

Aby stwierdzić, że $e$ zachowuje relację aproksymacji, niech $x\ll y$ w $D$. Załóżmy, że dla pewnego zbioru skierowanego $A\subseteq E$ mamy $e(y)⊑\bigvee {}^{\uparrow }A$. Wtedy $y⊑p(\bigvee {}^{\uparrow }A)=\bigvee {}^{\uparrow }p[A]$. Ten ostatni zbiór jest skierowany, więc istnieje $a\in A$ taki, że $x⊑p(a)$ - z definicji relacji aproksymacji, oczywiście. A zatem $e(x)⊑e(p(a))⊑a$, co dowodzi, że $e(x)\ll e(y)$.

Pokażmy na koniec, że $e(c)=\mathrm{m}\mathrm{i}\mathrm{n}{p}^{-1}[\uparrow x]$ dla $x\in D$ (dowód na postać $p$ jest analogiczny, więc go pominiemy). Oczywiście $x\in \uparrow x$, tzn. $p(e(x))\in \uparrow x$. A zatem $e(x)\in p^{-1}[\uparrow x]$. Ale jeśli $z\in p^{-1}[\uparrow x]$, to $p(z)\in \uparrow x$, czyli $x⊑p(z)$. Stąd $e(x)⊑e(p(z))⊑z$. To kończy dowód.

==Zadanie 2.9==

Udowodnij, że w $\mathbf{𝐓}\mathbf{𝐨}\mathbf{𝐩}$ morfizm $r:A\to C$ jest retrakcją wtedy i tylko wtedy, gdy jest retrakcją topologiczną, tj.: Istnieje podprzestrzeń $B$ przestrzeni $A$ oraz $e:A\to B$ ciągła oraz $h:B\to C$ homeomorfizm takie, że

$\mathrm{\forall }a\in Be(a)=a$

oraz diagram

komutuje.

Rozwiązanie:

Niech $r$ będzie retrakcją w $\mathbf{𝐓}\mathbf{𝐨}\mathbf{𝐩}$. Istnieje sekcja $s:C\to A$, tzn. $rs=1_C$. Definiujemy:

$B:=\{s(c)\mid c\in C\}$

wraz z topologią indukowaną z $A$. Zauważmy, że funkcja $e(a):=s(r(a))$ ma własność $\mathrm{\forall }a\in Be(a)=a$, ponieważ: $e(s(c))=srs(c)=s(c)$. Co więcej, jest ciągła jako złożenie funkcji ciągłych. Inna funkcja $h:=r{}_{\mid }B$ spełnia: $hs(c)=rs(c)=c$ oraz $sh(s(c))=shs(c)=srs(c)=s(c)$, jest więc dobrze określoną bijekcją z odwrotnością $s$. Jest też funkcją ciągłą i otwartą, czyli homeomorfizmem.

Odwrotnie, niech $r:A\to C$ faktoryzuje się, jak na diagramie powyżej. Definiujemy $s(c):=i(h^{-1})(c)$, gdzie $i:B\to A$ jest zanurzeniem (jest to funkcja ciągła, bo $B$ ma topologię podprzestrzeni $A$). Mamy $rs(c)=ri{h}^{-1}(c)=hei{h}^{-1}(c)=h{h}^{-1}(c)=c$, a zatem $r$ jest retrakcją w $\mathbf{𝐓}\mathbf{𝐨}\mathbf{𝐩}$.

W całym dowodzie pozwoliliśmy sobie dla prostoty opuścić symbol złożenia funkcji.