Analiza matematyczna 2/Ćwiczenia 5: Szereg potęgowy. Trygonometryczny szereg Fouriera

Szeregi potęgowe. Szeregi trygonometryczne Fouriera

Ćwiczenie 5.1.

Wyznaczyć promień zbieżności oraz przedział zbieżności dla następujących szeregów potęgowych:
(1) $\sum _{n=1}^{\mathrm{\infty }}{5}^n{x}^n,$
(2) $\sum _{n=1}^{\mathrm{\infty }}\frac{(x-2{)}^n}{(n+5)3^n},$
(3) $\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n{x}^n}{n},$
(4) $\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n(x+3{)}^n}{n^2}.$

Wskazówka

(1)-(4) Wyznaczyć promień zbieżności szeregów, stosując odpowiedni wzór (patrz twierdzenie 5.7.). Osobno zbadać zbieżność szeregów na końcach przedziału zbieżności.

Rozwiązanie

(1) Liczymy

$\kappa =\lim {}_{n\to +\mathrm{\infty }}\sqrt[n]{|a_n|}=\lim {}_{n\to +\mathrm{\infty }}\sqrt[n]{5^n}=\lim {}_{n\to +\mathrm{\infty }}5=5.$

Zatem promieniem zbieżności jest $R=\frac{1}{\kappa }=\frac{1}{5}.$ Szereg jest zatem zbieżny dla $x\in (-\frac{1}{5},\frac{1}{5})$ i rozbieżny dla $x\in \mathbb{ℝ}\setminus [-\frac{1}{5},\frac{1}{5}].$ Należy sprawdzić jego zbieżność dla $x=-\frac{1}{5}$ oraz $x=\frac{1}{5}.$

Dla $x=-\frac{1}{5}$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}(-1{)}^n,$ który jest rozbieżny (gdyż nie spełnia warunku koniecznego zbieżności szeregów), natomiast dla $x=\frac{1}{5}$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}1,$ który jest rozbieżny (z tego samego powodu).
Odpowiedź: Promień zbieżności wynosi $R=\frac{1}{5},$ a przedziałem zbieżności jest $(-\frac{1}{5},\frac{1}{5}).$

(2) Liczymy

$\kappa =\lim {}_{n\to +\mathrm{\infty }}\sqrt[n]{|a_n|}=\lim {}_{n\to +\mathrm{\infty }}\sqrt[n]{\frac{1}{(n+5)3^n}}=\frac{1}{3}\lim {}_{n\to +\mathrm{\infty }}\frac{1}{\sqrt[n]{n+5}}=\frac{1}{3}.$

Zatem promieniem zbieżności jest $R=\frac{1}{\kappa }=3.$ Szereg jest zatem zbieżny dla $x\in (2-3,2+3)=(-1,5)$ (gdyż środkiem tego szeregu jest $x_0=2$) i rozbieżny dla $x\in \mathbb{ℝ}\setminus [-1,5].$ Należy sprawdzić jego zbieżność dla $x=-1$ oraz $x=5.$

Dla $x=-1$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}\frac{(-3{)}^n}{(n+5)3^n}=\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n}{n+5},$ który jest zbieżny (na mocy kryterium Leibniza; patrz Analiza matematyczna 1 wniosek 7.13.), natomiast dla $x=5$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}\frac{3^n}{(n+5)3^n}=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n+5}=\sum _{n=6}^{\mathrm{\infty }}\frac{1}{n},$ który jest rozbieżny (jako szereg harmoniczny).
Odpowiedź: Promień zbieżności wynosi $R=3,$ a przedziałem zbieżności jest $[-1,5).$

(3) Liczymy

$\kappa =\lim {}_{n\to +\mathrm{\infty }}\sqrt[n]{|a_n|}=\lim {}_{n\to +\mathrm{\infty }}\sqrt[n]{\frac{1}{n}}=\lim {}_{n\to +\mathrm{\infty }}\frac{1}{\sqrt[n]{n}}=1.$

Zatem promieniem zbieżności jest $R=\frac{1}{\kappa }=1.$ Szereg jest zatem zbieżny dla $x\in (-1,1)$ i rozbieżny dla $x\in \mathbb{ℝ}\setminus [-1,1].$ Należy sprawdzić jego zbieżność dla $x=-1$ oraz $x=1.$

Dla $x=-1$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n},$ który jest rozbieżny (jako szereg harmoniczny), natomiast dla $x=1$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n}{n},$ który jest zbieżny (jako szereg anharmoniczny).
Odpowiedź: Promień zbieżności wynosi $R=1,$ a przedziałem zbieżności jest $(-1,1].$

(4) Liczymy

$\kappa =\lim {}_{n\to +\mathrm{\infty }}\sqrt[n]{|a_n|}=\lim {}_{n\to +\mathrm{\infty }}\sqrt[n]{\frac{1}{n^2}}=\frac{1}{3}\lim {}_{n\to +\mathrm{\infty }}\frac{1}{(\sqrt[n]{n}{)}^2}=1.$

Zatem promieniem zbieżności jest $R=\frac{1}{\kappa }=1.$ Szereg jest zatem zbieżny dla $x\in (-3-1,-3+1)=(-4,-2)$ (gdyż środkiem tego szeregu jest $x_0=-3$) i rozbieżny dla $x\in \mathbb{ℝ}\setminus [-4,-2].$ Należy sprawdzić jego zbieżność dla $x=-4$ oraz $x=-2.$

Dla $x=-4$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2},$ który jest zbieżny (jako uogólniony harmoniczny z wykładnikiem $\alpha =2>1$; patrz Analiza matematyczna 1 przykład 6.15.), natomiast dla $x=-2$ mamy szereg $\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n}{n^2},$ który jest zbieżny (gdyż jest bezwzględnie zbieżny).
Odpowiedź: Promień zbieżności wynosi $R=1,$ a przedziałem zbieżności jest $[-4,-2].$

Ćwiczenie 5.2.

Rozwinąć następujące funkcje w szereg Taylora o środku w podanym punkcie $x_0,$ bez obliczania pochodnych funkcji:
(1) $f(x)=x^7+11x^6+5x^4-3x^2+2,$
(2) $f(x)=x^2{e}^x,x_0=0.$

Wskazówka

(1) Co to jest szereg Taylora? Czy rozwinięcie w szereg Taylora jest jednoznaczne?
(2) Znamy już rozwinięcie funkcji $g(x)=e^x$ w szereg Maclaurina.

Rozwiązanie

(1) Ponieważ funkcja $f$ jest wielomianem, więc z jednoznaczności przedstawienia funkcji w szereg potęgowy wynika, że jest ona swoim szeregiem Maclaurina

$S(x)=f(x)=f(x)=x^7+11x^6+5x^4-3x^2+2.$

(2) Ponieważ znamy już szereg Maclaurina dla funkcji $g(x)=e^x$:

$g(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!},$

zatem

$S(x)=x^2{e}^x=\sum _{n=0}^{\mathrm{\infty }}\frac{x^{n+2}}{n!}=\sum _{n=2}^{\mathrm{\infty }}\frac{x^n}{(n-2)!}$

jest szeregiem Maclaurina dla funkcji $f.$

Ćwiczenie 5.3.

Rozwinąć następujące funkcje w szereg Taylora o środku w podanym punkcie $x_0,$ bez obliczania pochodnych funkcji:
(1) $f(x)=\frac{1}{1-x},x_0=0,$
(2) $f(x)=\frac{1}{x^2+4x+7},x_0=-2,$
(3) $f(x)=\frac{1}{1+x^3},x_0=0.$

Wskazówka

(1) Należy zauważyć, że funkcja $f$ dla każdego $x$ (bliskiego $x_0$) jest sumą pewnego znanego nam szeregu liczbowego.
(2) Zapisać trójmian kwadratowy w mianowniku w postaci kanonicznej i zauważyć, że funkcja $f$ jest sumą pewnego znanego nam szeregu liczbowego.
(3) Zrobić podobnie jak (1).

Rozwiązanie

(1) Zauważmy, że wyrażenie $\frac{1}{1-x}$ jest sumą szeregu geometrycznego $\sum _{n=0}^{\mathrm{\infty }}{x}^n,$ gdy $|x|<1.$ Ponieważ rozwinięcie funkcji w szereg potęgowy jest jednoznaczne, więc jest to szereg Maclaurina funkcji $f$:

$S(x)=\sum _{n=0}^{\mathrm{\infty }}{x}^n.$

(2) Zauważmy, że

$f(x)=\frac{1}{x^2+4x+7}=\frac{1}{(x+2{)}^2+3}=\frac{\frac{1}{3}}{(\frac{x+2}{\sqrt{3}}{)}^2+1}.$

Zauważmy, że powyższe wyrażenie jest sumą szeregu geometrycznego o pierwszym wyrazie $\frac{1}{3}$ i ilorazie $-(\frac{x+2}{\sqrt{3}}{)}^2.$ Zatem następujący szereg $S$ jest zbieżny do funkcji $f$ (gdy $\left|\frac{x+2}{\sqrt{3}}\right|<1$)

$S(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{3}(-(\frac{x+2}{\sqrt{3}}{)}^2{)}^n=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{3^{n+1}}(x+2{)}^{2n}.$

Ale powyższy szereg jest szeregiem potęgowym o środku $x_0=-2.$ Ponieważ rozwinięcie funkcji w szereg potęgowy jest jednoznaczne, więc jest to szukany szereg Taylora funkcji $f$ o środku w punkcie $x_0=-2.$

(3) Zauważmy, że wyrażenie $\frac{1}{1+x^3}$ jest sumą szeregu geometrycznego $\sum _{n=0}^{\mathrm{\infty }}(-x^3{)}^n,$ gdy $|-x^3|<1,$ czyli dla $x\in (-1,1).$ Ponieważ rozwinięcie funkcji w szereg potęgowy jest jednoznaczne, więc szeregiem Maclaurina funkcji $f$ jest:

$S(x)=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n{x}^{3n}.$

Ćwiczenie 5.4.

Rozwinąć następującą funkcję $f(x)=\frac{1}{(1-x{)}^2}$ w szereg Maclaurina.

Wskazówka

Funkcja jest pochodną funkcji z ćwiczenia 5.3. (z dokładnością do znaku). Skorzystać z twierdzenia o różniczkowaniu szeregu potęgowego wyraz po wyrazie (patrz twierdzenie 5.10.).

Rozwiązanie

Zauważmy, że

$\frac{1}{(1-x{)}^2}=-(\frac{1}{1-x}{)}^{\prime }.$

Korzystając z rozwinięcia funkcji $\frac{1}{1-x}$ w szereg Maclaurina (patrz ćwiczenia 5.3. (1)) oraz z twierdzenia o różniczkowaniu szeregu potęgowego wyraz po wyrazie (patrz twierdzenie 5.10.), mamy

$\begin{array}{lll}\frac{1}{(1-x{)}^2}& =& -(\frac{1}{1-x}{)}^{\prime }=-(\sum _{n=0}^{\mathrm{\infty }}{x}^n{)}^{\prime }\\ & =& -\sum _{n=1}^{\mathrm{\infty }}n{x}^{n-1}=-\sum _{n=0}^{\mathrm{\infty }}(n+1)x^n.\end{array}$

Ćwiczenie 5.5.

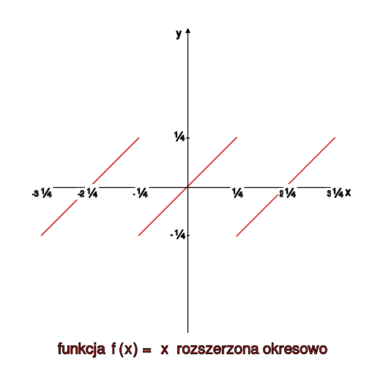
Rozwinąć w szereg Fouriera funkcję $f(x)=x$ zadaną na przedziale $(-\pi ,\pi ].$

Wskazówka

Rozszerzyć funkcję do funkcji określonej na całym $\mathbb{ℝ}$ i zastosować wzory Eulera-Fouriera. W obliczeniach należy użyć wzoru na całkowanie przez części.

Rozwiązanie

Rozszerzamy naszą funkcję do funkcji określonej na całym $\mathbb{ℝ},$ dostajemy funkcję z rysunku poniżej:

Następnie liczymy współczynniki szeregu Fouriera:

$a_0=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}xdx=\frac{1}{4\pi }{x}^2{|}_{-\pi }^{\pi }=0.$

Dla $m=1,2,\dots$ liczymy $a_m$ i $b_m$:

$a_m=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}x\cos (mx)dx=$

tu całkujemy przez części ($u(x)=x,v^{\prime }(x)=\cos (mx)$)

$=\frac{1}{\pi }x\frac{\sin (mx)}{m}{|}_{-\pi }^{\pi }-\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}\frac{\sin (mx)}{m}dx=\frac{1}{\pi }\frac{\cos (mx)}{m}{|}_{-\pi }^{\pi }=\frac{1}{\pi }(\frac{\cos (m\pi )}{m}-\frac{\cos (m(-\pi ))}{m})=0.$

Licząc analogicznie, mamy

$\begin{array}{rl}{b}_m& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}x\sin (mx)dx=-\frac{1}{\pi }x\frac{\cos (mx)}{m}{|}_{-\pi }^{\pi }+\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}\frac{\cos (mx)}{m}dx\\ & =-(\frac{1}{\pi }\pi \frac{\cos (m\pi )}{m}-\frac{1}{\pi }(-\pi )\frac{\cos (m(-\pi ))}{m})+\frac{1}{m\pi }\underset{-\pi }{\overset{\pi }{\int }}\cos (mx)=\frac{2}{m}(-1{)}^{m+1}+\frac{1}{m^2\pi }\sin (mx){|}_{-\pi }^{\pi }\\ & =\frac{2}{m}(-1{)}^{m+1}.\end{array}$

A zatem szereg Fouriera funkcji $f(x)=x$ w przedziale $(-\pi ,\pi ]$ jest dany wzorem

$\sum _{m=1}^{\mathrm{\infty }}\frac{2(-1{)}^{m+1}}{m}\sin (mx).$

Funkcja $f(x)=x$  rozszerzona okresowo

Plik:Am2.m05.c.r01.svg Kolejna przybliżenia funkcji $f(x)=x$

Uwaga: Z kryterium Dirichleta (patrz twierdzenie 5.18.) wynika, że ten szereg jest zbieżny do $f$ na całym przedziale otwartym $(-\pi ,\pi ).$ Na końcach przedziału suma szeregu wynosi (oczywiście!) zero, także zgodnie z kryterium Dirichleta (patrz twierdzenie 5.18.).

Ćwiczenie 5.6.

Wykazać, że szereg Fouriera funkcji parzystej (całkowalnej i okresowej o okresie $2\pi$) zawiera same cosinusy, a funkcji nieparzystej same sinusy.

Wskazówka

Najpierw wykazać, że jeśli $g(x)$ jest funkcją daną w przedziale $[-\pi ,\pi ],$ całkowalną i nieparzystą, to

$\underset{-\pi }{\overset{\pi }{\int }}g(x)dx=0$

Rozwiązanie

Niech $g(x)$ będzie funkcją daną w przedziale $[-\pi ,\pi ],$ całkowalną i nieparzystą. Wówczas

$\underset{-\pi }{\overset{\pi }{\int }}g(x)dx=\underset{-\pi }{\overset{0}{\int }}g(x)dx+\underset{0}{\overset{\pi }{\int }}g(x)dx=$

(stosujemy w pierwszej całce podstawienie $x=-t$)

$=\underset{\pi }{\overset{0}{\int }}g(-t)(-dt)+\underset{0}{\overset{\pi }{\int }}g(x)dx=-\underset{0}{\overset{\pi }{\int }}g(t)dt+\underset{0}{\overset{\pi }{\int }}g(x)dx=0.$

Niech teraz $f$ będzie funkcją parzystą. Wtedy $f(x)\sin (nx)$ jest funkcją nieparzystą. Zatem, stosując pierwszy udowodniony fakt, mamy

$b_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\sin (nx)dx=0,$

więc wszystkie współczynniki przy sinusach są równe zero.

Jeśli funkcja $f$ jest nieparzysta, to $f(x)\cos (nx)$ jest też funkcją nieparzystą i wtedy

$a_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\cos (nx)dx=0,$

a zatem znikają wszystkie współczynniki przy cosinusach.

Ćwiczenie 5.7.

Rozwinąć funkcję $f(x)=x,$ zadaną na przedziale $[0,\pi ]$ w szereg Fouriera zawierający same cosinusy.

Wskazówka

Takie sformułowanie zadania oznacza, że nie powinnytraktować naszej funkcji jako funkcji okresowej o okresie $\pi ,$ ale najpierw rozszerzyć ją do przedziału $[-\pi ,\pi ],$ a dopiero potem na całe $\mathbb{ℝ}.$ Oczywiście, to jak rozszerzymy funkcję do przedziału $[-\pi ,\pi ]$ zależy od tego, jaki szereg chcemy uzyskać. Z ćwiczenia 5.6. wynika, że szereg Fouriera funkcji parzystej będzie zawierał same cosinusy, a szereg Fouriera funkcji nieparzystej - same sinusy.

Rozwiązanie

Skorzystamy z ćwiczenia 5.6..

Jeśli zatem mamy rozwinąć funkcję $f(x)=x,$ zadaną na przedziale $[0,\pi ]$ w szereg Fouriera zawierający same cosinusy, to musimy najpierw przedłużyć ją na przedział $[-\pi ,\pi ]$ tak, by dostać funkcję parzystą. Funkcja przedłużona jest zatem określona wzorem

<flash>file=am2.m05.c.r02.swf|width=375|height=375</flash>

<div.thumbcaption>Aproksymacja funkcji $f(x)=|x|$  kolejnymi sumami szeregu Fouriera

$\tilde{f}(x)=\{\begin{array}{lll}x,& \text{dla}{\displaystyle }& x\in [0,\pi ]\\ -x,& \text{dla}{\displaystyle }& x\in [-\pi ,0].\end{array}$

Funkcję $\tilde{f}(x)$ rozszerzamy następnie okresowo na całe $\mathbb{ℝ}.$

Ze wzorów Eulera-Fouriera mamy:

$a_0=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}\tilde{f}(x)dx=\frac{1}{\pi }\underset{0}{\overset{\pi }{\int }}xdx=\frac{x^2}{2}{|}_0^{\pi }=\frac{\pi }{2}.$

Dla $n=1,2,\dots$

$a_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}\tilde{f}(x)\cos (nx)dx=\frac{2}{\pi }\underset{0}{\overset{\pi }{\int }}x\cos (nx)dx=$

(całkujemy przez części, $u(x)=x,v^{\prime }(x)=\cos (nx)$)

$=\frac{2}{\pi }x\frac{\sin (nx)}{n}{|}_0^{\pi }-\frac{2}{n\pi }\underset{0}{\overset{\pi }{\int }}\sin (nx)dx=\frac{2}{n^2\pi }(\cos (n\pi )-1).$

Zatem, skoro $\cos (n\pi )=(-1{)}^n,$ mamy

$a_{2k}=0,a_{2k-1}=\frac{-4}{(2k-1{)}^2\pi }.$

Oczywiście z powyższych rozważań wynika, że $b_n=0$ dla $n=1,2,\dots .$

Tak więc szukany szereg, to

$\frac{\pi }{2}+\sum _{k=1}^{\mathrm{\infty }}\frac{-4}{(2k-1{)}^2\pi }\cos ((2k-1)x).$

Ćwiczenie 5.8.

Policzyć sumę szeregu Leibniza:

$\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{2k-1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\dots$

Wskazówka

Należy wykorzystać ćwiczenie 5.5.

Rozwiązanie

Z ćwiczenie 5.5. (1) wiemy, jak wygląda szereg Fouriera funkcji $f(x)=x$ na przedziale $[-\pi ,\pi ].$ (Funkcja jest nieparzysta, więc nic dziwnego, że szereg zawiera same sinusy, porównaj z ćwiczeniem 5.6.) Z kryterium Dirichleta (patrz twierdzenie 5.18.) wynika, że dla $x\in (-\pi ,\pi )$ mamy równość:

$x=\sum _{m=1}^{\mathrm{\infty }}\frac{2(-1{)}^{m+1}}{m}\sin (mx).$

Wstawmy zatem $x=\frac{\pi }{2}.$ Dostaniemy:

$\frac{\pi }{2}=\sum _{m=1}^{\mathrm{\infty }}\frac{2(-1{)}^{m+1}}{m}\sin (m\frac{\pi }{2}).$

Zauważmy, że $\sin ((2k-2)\frac{\pi }{2})=0,\sin ((4k-3)\frac{\pi }{2})=1,\sin ((4k-1)\frac{\pi }{2})=-1,k=1,2,\dots ,$ a zatem naszą równość możemy zapisać tak:

$\frac{\pi }{2}=2\sum _{k=1}^{\mathrm{\infty }}(\frac{-1}{4k-1}+\frac{1}{4k-3})=2\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{2k-1}.$

To daje odpowiedź na nasze pytanie,

$\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{2k-1}=\frac{\pi }{4}.$

Ćwiczenie 5.9.

Rozwinąć w szereg Fouriera funkcję daną w przedziale $[-\pi ,\pi ]$ wzorem

$f(x)=\sin (2x)-3\cos (2x)+11\cos (5x)-0.1\sin (6x).$

Wskazówka

Rozwiązanie jest oczywiste.

Rozwiązanie

Plik:Am2.m05.c.r03.svg

Wykres funkcji $f$

Szereg Fouriera tej funkcji jest jej równy, bo ona już jest swoim (skończonym) szeregiem trygonometrycznym. (Należy zwrócić uwagę, że współczynniki w szeregu Fouriera są wyznaczone jednoznacznie, zatem jeśli znajdziemy jakieś przedstawienie funkcji w postaci szeregu trygonometrycznego, to mamy już rozwinięcie w szereg Fouriera).