Testy 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „<math> ” na „<math>” |
|||
| (Nie pokazano 126 wersji utworzonych przez 8 użytkowników) | |||
| Linia 4: | Linia 4: | ||
'''sdfdfsfdsdf''' | '''sdfdfsfdsdf''' | ||
[[tutaj link wewnętrzny-aaa]] | [[tutaj link wewnętrzny-aaa]] | ||
== ukrywajki zagnieżdzone == | |||
{{odpowiedz|| | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"> | |||
ukrywajka nr 1 | |||
<div class="mw-collapsible-content" style="display:none">1 ukrywajka | |||
druga ukrywajka | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"> | |||
<div class="mw-collapsible-content" style="display:none">druga...</div> | |||
</div> | |||
</div> | |||
</div> | |||
}} | |||
== cw == | |||
{{cwiczenie| 4|cw4| | |||
O pętli for można jednak myśleć jeszcze inaczej. Można wymagać, aby wszelkie zmiany wartości zmiennej sterującej <math>x</math> wewnątrz wykonania pętli nie miały wpływu na liczbę iteracji tej pętli. Przykładowo przy semantyce z poprzedniego zadania pętla: | |||
'''for''' x := 1 '''to''' 10 '''do''' | |||
x := x + 1; | |||
y := y + x; | |||
wykonuje się pięć razy, a zmienna y jest zwiększana łącznie o 2+4+6+8+10. Jeśli uznamy, że zmiany zmiennej x wewnątrz pętli nie wpływają na liczbę iteracji, to pętla wykona się 10 razy, a zmienna y zostanie zwiększona o 2+3+4+5+6+7+8+9+10+11. | |||
Zdefiniuj taką semantykę. | |||
}} | |||
<table> | |||
<tr> | |||
<td> asnas </td> <td> 2gi </td> | |||
</tr> | |||
</table> | |||
== Obrazek == | |||
[[Image:ryc1.jpg||thumbnail|45px||1.Geometryczne rozwiązanie równania ]] | |||
[[Image:wykres1.jpg|thumb|111px|Enter the name of an image from Commons on any MediaWiki installation ..]] | |||
[[Image:ryc1b.jpg||thumb|right|200px|2.Geometryczne rozwiązanie równania <math>x^2+10x=39</math>]] | |||
[[Grafika:ryc1c.jpg|thumb|right|3.Geometryczne rozwiązanie równania <math>x^2+10x=39</math>]] | |||
[[Grafika:ryc1d.gif|thumb|right|200px|4.GIFeometryczne rozwiązanie równania <math>x^2+10x=39</math>]] | |||
[[image:r_do_n.png|left|noframe||ala ma kota]] | |||
<center> | |||
la la la pod spodem flash | |||
</center> | |||
<flash>file=Klocki.swf|width=450|height=250</flash> | |||
la la la | |||
a tu prezentacja | |||
<flash>file=Wektor.swf|width=640|height=480</flash> | |||
== test == | |||
[[Grafika:narzedzia.jpg]] | |||
[[Grafika:nuty.jpg]] | |||
[[Grafika:kroki.jpg]] | |||
[[Grafika:narzedzia2.jpg]] | |||
[[Grafika:przepis.jpg]] | |||
[[Grafika:mapa.jpg]] | |||
[[Grafika:wykres1.jpg]] | |||
*1 | |||
**1.1 | |||
***1.1.1 | |||
**? | |||
***?*1 | |||
**1.1 | |||
***1.1.1 | |||
**? | |||
***?*1 | |||
**1.1 | |||
***1.1.1 | |||
**? | |||
***?*1 | |||
**1.1 | |||
***1.1.1 | |||
**? | |||
***? | |||
=Wykresy do akcptacji:= | |||
[[Image:wykres2.gif|thumb|to jest wykres nr1]] | |||
[[Image:wykres2.jpg|thumb|left|Middle East; for more detailed pdf-version see [http://www.cia.gov/cia/publications/factbook/reference_maps/pdf/middle_east.pdf]]] | |||
[[Grafika:wykres2.jpg]] | |||
[[Grafika:wykres3.jpg]] | |||
== Headline text == | == Headline text == | ||
| Linia 14: | Linia 104: | ||
[[Testy_2/Podtest1/Podtest2]] | [[Testy_2/Podtest1/Podtest2]] | ||
[[Testy_2/Podtest1]] | [[Testy_2/Podtest1]] | ||
---- | |||
*[[testy_2/Wykład01]] | |||
*[[testy_2wykład01-podejście2]] | |||
*[[testy_2/Wykład04]] | |||
==rozdz== | ==rozdz== | ||
| Linia 24: | Linia 118: | ||
***? | ***? | ||
<math> | <math> | ||
\frac{\alpha}{\beta} | \frac{\alpha}{\beta} | ||
</math> | </math> | ||
==linia== | ==linia== | ||
[[FilmFlashDemo2|Demo2]] | [[FilmFlashDemo2|Demo2]] | ||
=Podstawowe pojęcia i definicje= | |||
\label{sec:podstawy} | \label{sec:podstawy} | ||
Powyżej widzimy tytuł naszego przedmiotu, następnie jego autora oraz datę | Powyżej widzimy tytuł naszego przedmiotu, następnie jego autora oraz datę | ||
pochodzenia bieżącej wersji, generowaną automatycznie. | pochodzenia bieżącej wersji, generowaną automatycznie. | ||
Dane o przedmiocie i autorze definiujemy w pliku \lstux!dane.tex!: | Dane o przedmiocie i autorze definiujemy w pliku \lstux!dane.tex!: | ||
\begin{latex} | \begin{latex} | ||
\title{Geometria inaczej} | \title{Geometria inaczej} | ||
\author{Piotr Goras} | \author{Piotr Goras} | ||
\date{Wersja z \today} | \date{Wersja z \today} | ||
\hyperbaseurl{http://osilek.mimuw.edu.pl} % link do strony naszego przedmiotu | \hyperbaseurl{http://osilek.mimuw.edu.pl} % link do strony naszego przedmiotu | ||
\end{latex} | \end{latex} | ||
{{definicja|Trójkąt prostokątny|dfn:kat_prosty|'''Trójkątem prostokątnym''' nazywamy taki trójkąt, który ma przynajmniej jeden kątprosty. | |||
{{definicja|Trójkąt prostokątny|dfn:kat_prosty| | |||
'''Trójkątem prostokątnym''' nazywamy taki trójkąt, który ma przynajmniej jeden | |||
}} | }} | ||
{{twierdzenie|Pitagoras|thm:pitagoras| | {{twierdzenie|Pitagoras|thm:pitagoras| | ||
W trójkącie prostokątnym o przyprostokątnych <math>a</math>, <math>b</math> i przeciwprostokątnej <math>c</math> | W trójkącie prostokątnym o przyprostokątnych <math>a</math>, <math>b</math> i przeciwprostokątnej <math>c</math> | ||
zawsze zachodzi | zawsze zachodzi | ||
<math>a^2+b^2 = c^2</math>, | |||
<math> | zob. rys. \ref{rys:trojkat} | ||
a^2+b^2 = c^2 | |||
</math> | |||
zob. rys. | |||
}} | }} | ||
\rysunek{trojkat}{Ilustracja twierdzenia Pitagorasa.} | \rysunek{trojkat}{Ilustracja twierdzenia Pitagorasa.} | ||
Rysunki akceptujemy tylko w formacie PNG. Zdjęcia mogą także być w formacie JPG. | Rysunki akceptujemy tylko w formacie PNG. Zdjęcia mogą także być w formacie JPG. | ||
\begin{proof} | \begin{proof} | ||
Ble, ble. | Ble, ble. | ||
\end{proof} | \end{proof} | ||
W twierdzeniu \ref{thm:pitagoras} widać, jak można wykorzystać | |||
definicję \ref{dfn:kat_prosty} do tego, by sformułować je bez potrzeby | |||
W twierdzeniu | |||
definicję | |||
stosowania \osiref{Analiza matematyczna}{miary Kąt'a}. | stosowania \osiref{Analiza matematyczna}{miary Kąt'a}. | ||
{{stwierdzenie|||Nie każdy trójkąt jest prosty. | |||
{{stwierdzenie||| | |||
Nie każdy trójkąt jest prosty. | |||
}} | }} | ||
{{wniosek|||Są trójkąty o bokach długości <math>a</math>, <math>b</math>, <math>c</math>, dla których <math>a^2 + b^2 \neq c^2</math>. | |||
{{wniosek||| | |||
Są trójkąty o bokach długości <math>a</math>, <math>b</math>, <math>c</math>, dla których <math>a^2 + b^2 \neq c^2</math>. | |||
}} | }} | ||
{{uwaga|||To nie jest cała prawda o trójkątach! Dodatkowo, wiemy, że: | |||
{{uwaga||| | |||
To nie jest cała prawda o trójkątach! Dodatkowo, wiemy, że: | |||
#w każdym trójkącie o bokach <math>a</math>, <math>b</math>, <math>c</math> zachodzi: | #w każdym trójkącie o bokach <math>a</math>, <math>b</math>, <math>c</math> zachodzi: | ||
#;<math>a+b \geq c | |||
#;<math> | </math> | ||
#; | #; | ||
#suma kątów w trójkącie jest większa od 90 stopni | #suma kątów w trójkącie jest większa od 90 stopni | ||
#; | #; | ||
#itd. | #itd. | ||
#; | #; | ||
}} | }} | ||
==Równania== | |||
\begin{latex} | \begin{latex} | ||
<math>a + b = c | |||
<math> | |||
a + b = c | |||
</math> | </math> | ||
\end{latex} | \end{latex} | ||
daje | daje | ||
<math>a + b = c | |||
</math> | |||
<math>a + b = c, \textcolor{red}{text in blue} | |||
</math> | </math> | ||
daje | daje | ||
<math>a + b = c, | |||
</math> | |||
a + b = c | |||
\begin{latex} | \begin{latex} | ||
\begin{align} | \begin{align} | ||
a + b &= c\\ | a + b &= c\\ | ||
c + d + e &= f | c + d + e &= f | ||
\end{align} | \end{align} | ||
\end{latex} | \end{latex} | ||
daje | daje | ||
\begin{align} | \begin{align} | ||
a + b &= c\\ | a + b &= c\\ | ||
c + d + e &= f | c + d + e &= f | ||
\end{align} | \end{align} | ||
==Hiperłącza== | |||
\label{sec:hiper} | \label{sec:hiper} | ||
\url{http://www.mimuw.edu.pl} | \url{http://www.mimuw.edu.pl} | ||
\href{http://www.mimuw.edu.pl}{Wydział Matematyki} | |||
\href{wyklad1.html}{Link do podstrony w naszym przedmiocie} | |||
\ | ==Inne informacje== | ||
\label{sec:inne} | |||
{{przyklad|||ala ma kota <math>y + x = \sin(z)</math> ala ma kota yy}} | |||
ala ma kota <math>\phi + y^{k} + x = \sin(z)</math> ala ma kota yy | |||
{{cwiczenie| 4|cw4| | |||
O pętli for można jednak myśleć jeszcze inaczej. Można wymagać, aby wszelkie zmiany wartości zmiennej sterującej <math>x</math> wewnątrz wykonania pętli nie miały wpływu na liczbę iteracji tej pętli. Przykładowo przy semantyce z poprzedniego zadania pętla: | |||
'''for''' x :<nowiki>=</nowiki> 1 '''to''' 10 '''do''' | |||
x :<nowiki>=</nowiki> x + 1; | |||
y :<nowiki>=</nowiki> y + x; | |||
wykonuje się pięć razy, a zmienna y jest zwiększana łącznie o 2+4+6+8+10. Jeśli uznamy, że zmiany zmiennej x wewnątrz pętli nie wpływają na liczbę iteracji, to pętla wykona się 10 razy, a zmienna y zostanie zwiększona o 2+3+4+5+6+7+8+9+10+11. | |||
Zdefiniuj taką semantykę. | |||
}} | |||
==test== | |||
{{ | |||
twierdzenie|[Twierdzenie Pitagorasa]|pitagoras| | |||
W trójkącie prostokątnym o przyprostokątnych <math>a</math>, <math>b</math> i przeciwprostokątnej <math>c</math> | |||
<table border=1><tr><td>la la la </td></tr></table> | |||
zawsze zachodzi | |||
<math>a^2+b^2 = c^2 | |||
</math>. | |||
}} | |||
[[KolejnaStronaTestow]] | |||
Aktualna wersja na dzień 22:14, 11 wrz 2023
Strona do testów pochylony tekst?? a to jaki? gruby :) sdfdfsfdsdf tutaj link wewnętrzny-aaa
ukrywajki zagnieżdzone
Odpowiedź
{{{2}}}
cw
Ćwiczenie 4
{{{3}}}
| asnas | 2gi |
Obrazek
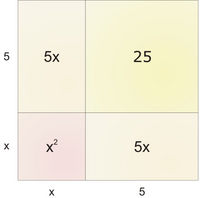
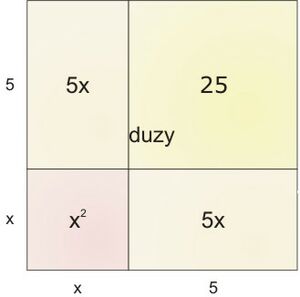
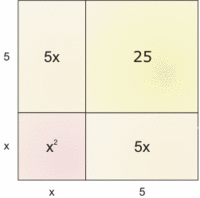
la la la pod spodem flash
<flash>file=Klocki.swf|width=450|height=250</flash>
la la la a tu prezentacja
<flash>file=Wektor.swf|width=640|height=480</flash>
test
- 1
- 1.1
- 1.1.1
- ?
- ?*1
- 1.1
- 1.1.1
- ?
- ?*1
- 1.1
- 1.1.1
- ?
- ?*1
- 1.1
- 1.1.1
- ?
- ?
- 1.1
Wykresy do akcptacji:
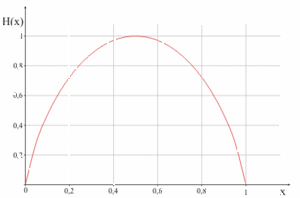
Headline text
Template:moj szablon
Testy_2/Podtest1/Podtest2 Testy_2/Podtest1
rozdz
rozdz
rozdzialik
- 1
- 1.1
- 1.1.1
- ?
- ?
- 1.1
linia
Podstawowe pojęcia i definicje
\label{sec:podstawy}
Powyżej widzimy tytuł naszego przedmiotu, następnie jego autora oraz datę pochodzenia bieżącej wersji, generowaną automatycznie.
Dane o przedmiocie i autorze definiujemy w pliku \lstux!dane.tex!:
\begin{latex} \title{Geometria inaczej} \author{Piotr Goras} \date{Wersja z \today} \hyperbaseurl{http://osilek.mimuw.edu.pl} % link do strony naszego przedmiotu \end{latex}
Definicja Trójkąt prostokątny
Trójkątem prostokątnym nazywamy taki trójkąt, który ma przynajmniej jeden kątprosty.
Twierdzenie Pitagoras
W trójkącie prostokątnym o przyprostokątnych , i przeciwprostokątnej zawsze zachodzi , zob. rys. \ref{rys:trojkat}
\rysunek{trojkat}{Ilustracja twierdzenia Pitagorasa.}
Rysunki akceptujemy tylko w formacie PNG. Zdjęcia mogą także być w formacie JPG.
\begin{proof} Ble, ble. \end{proof}
W twierdzeniu \ref{thm:pitagoras} widać, jak można wykorzystać definicję \ref{dfn:kat_prosty} do tego, by sformułować je bez potrzeby stosowania \osiref{Analiza matematyczna}{miary Kąt'a}.
Stwierdzenie
Nie każdy trójkąt jest prosty.
Wniosek
Są trójkąty o bokach długości , , , dla których .
Uwaga
To nie jest cała prawda o trójkątach! Dodatkowo, wiemy, że:
- w każdym trójkącie o bokach , , zachodzi:
- suma kątów w trójkącie jest większa od 90 stopni
- itd.
Równania
\begin{latex} \end{latex}
daje
Parser nie mógł rozpoznać (nieznana funkcja „\textcolor”): {\displaystyle a + b = c, \textcolor{red}{text in blue} }
daje
\begin{latex} \begin{align} a + b &= c\\ c + d + e &= f \end{align} \end{latex}
daje \begin{align} a + b &= c\\ c + d + e &= f \end{align}
Hiperłącza
\label{sec:hiper}
\href{http://www.mimuw.edu.pl}{Wydział Matematyki}
\href{wyklad1.html}{Link do podstrony w naszym przedmiocie}
Inne informacje
\label{sec:inne}
Przykład
ala ma kota ala ma kota yy
ala ma kota ala ma kota yy
Ćwiczenie 4
O pętli for można jednak myśleć jeszcze inaczej. Można wymagać, aby wszelkie zmiany wartości zmiennej sterującej wewnątrz wykonania pętli nie miały wpływu na liczbę iteracji tej pętli. Przykładowo przy semantyce z poprzedniego zadania pętla:
for x := 1 to 10 do x := x + 1; y := y + x;
wykonuje się pięć razy, a zmienna y jest zwiększana łącznie o 2+4+6+8+10. Jeśli uznamy, że zmiany zmiennej x wewnątrz pętli nie wpływają na liczbę iteracji, to pętla wykona się 10 razy, a zmienna y zostanie zwiększona o 2+3+4+5+6+7+8+9+10+11. Zdefiniuj taką semantykę.
test
Twierdzenie [Twierdzenie Pitagorasa]
{{{3}}}
