Teoria kategorii dla informatyków/Wykład 12: Teoria dziedzin I

Dziedziny jako częściowe porządki

Ten wykład jest wprowadzeniem w teorię dziedzin, którą zapoczątkowały badania Dany Scotta i Christophera Stracheya nad semantyką funkcyjnych języków programowania pod koniec lat 60. Dziedziny są to pewne częściowe porządki, które posiadają suprema zbiorów skierowanych i dodatkową relację binarną nazywaną relacją aproksymacji. Przeróżne kategorie dziedzin zostały wykorzystane jako matematyczne modele języków programowania, w sensie, który wyjaśnimy w Wykładzie 13. Kategorie dziedzin są znakomitym uniwersum, w którym za pomocą ścisłych matematycznych metod można opisywać rekursywne definicje procedur, struktur danych i innych mechanizmów języków programowania.

Uwaga dla dociekliwych

Klasycznym przykładem jest tu język nietypowanego $\lambda$-rachunku. Aby stworzyć semantykę tego języka, należy zaproponować pewną kategorię składającą się z obiektów typu $D$ w taki sposób, aby termy $\lambda$-rachunku były interpretowane jako elementy $D$, zaś aplikacja funkcji do argumentu była rozumiana jako aplikacja strzałki $f:D\to E$ do argumentu typu $D$. Jeśli teraz rozważymy $\lambda$-term $\lambda x.xx$, widzimy, że pierwsze wolne wystąpienie $x$ musi być typu $D\to D$, zaś drugie typu $D$. A zatem musimy wymagać, by $D\cong [D,D]$. W naszej kategorii semantycznej muszą zatem istnieć nietrywialne punkty stałe funktora $[,]$. Pokażemy, że to możliwe w Wykładzie 14.

Ten wykład wprowadza wszystkie wstępne pojęcia teorii dziedzin w języku częściowych porządków i jest niezależny od wcześniejszych wykładów.

Dziedziny jako częściowe porządki

Porządek (inaczej: częściowy porządek, zbiór częściowo uporządkowany, poset) to zbiór wyposażony w relację $⊑$, która jest zwrotna, przechodnia i antysymetryczna.

Niech

$(P,⊑)$

będzie częściowym porządkiem. Element

$a\in P$

jest ograniczeniem górnym zbioru

$X\subseteq P$

, jeśli

$x⊑a$

dla każdego

$x\in X$

(co zapisujemy również

$X⊑a$

). Podobnie, element

$b\in P$

jest ograniczeniem dolnym zbioru

$X⊑P$

, jeśli

$b⊑x$

dla każdego

$x\in X$

(czyli

$b⊑X$

). Jeśli dwa dowolne elementy

$x,y\in P$

posiadają w

$P$

ograniczenie górne, to oznaczamy to jako

$x\uparrow y$

. W przeciwnym wypadku piszemy

$x\mathrm{\#}y$

. Najmniejsze ograniczenie górne zbioru

$X\subseteq P$

(jeśli istnieje) nazywamy supremum

$X$

i oznaczamy

$\bigvee X$

. Największe ograniczenie dolne zbioru

$X\subseteq P$

(jeśli istnieje) nazywamy infimum

$X$

i oznaczamy

$\bigwedge X$

. Jeśli

$X\subseteq P$

jest dwuelementowy, np.

$X=\{x,y\}$

, i posiada supremum (infimum), to piszemy

$\bigvee X=x\vee y$

(

$\bigwedge X=x\wedge y$

) i mówimy o supremum (infimum) binarnym.

Dana S. Scott ur. 1932
Zobacz biografię

Poset jest kratą, jeśli ma wszystkie suprema i infima binarne. Poset jest kratą zupełną, jeśli dowolny jego podzbiór posiada zarówno supremum, jak i infimum.

Podzbiór $D$ porządku $P$ nazywamy skierowanym, co oznaczamy $D{\subseteq }^{\uparrow }P$, jeśli jest niepusty i każde dwa elementy z $D$ posiadają ograniczenie górne w $D$ (tzn. $D\ne \mathrm{\varnothing }$ i $x,y\in D\Rightarrow x,y⊑z$ dla pewnego $z\in D$). Łańcuchem nazywamy każdy zbiór skierowany, który jest liniowy. Supremum zbioru skierowanego $D{\subseteq }^{\uparrow }P$ oznaczamy ${\bigvee }^{\uparrow }D$, kiedykolwiek istnieje. Podzbiór $F$ porządku $P$ nazywamy filtrowanym, jeśli jest niepusty i każde dwa elementy z $F$ posiadają ograniczenie dolne w $F$ (tzn. $F\ne \mathrm{\varnothing }$ i $x,y\in F\Rightarrow z⊑x,y$ dla pewnego $z\in F$). Infimum zbioru filtrowanego $F$ (jeśli istnieje) oznaczamy $\underset{\downarrow }{\bigwedge }F$.

Poset $P$ nazywamy $bc$-zupełnym, jeśli $P$ posiada element najmniejszy $\mathrm{\perp }$ oraz każde dwa elementy $x,y\in P$ takie, że $x\uparrow y$, posiadają supremum $x\vee y\in P$.

Oznaczamy:

$\downarrow X=\{z\in P\mid \mathrm{\exists }x\in X\mid z⊑x\}$

$\uparrow X=\{w\in P\mid \mathrm{\exists }x\in X\mid x⊑w\}$

$\downarrow x=\downarrow \{x\}$

$\uparrow x=\uparrow \{x\}$

$X\subseteq P$ jest zbiorem dolnym, jeśli $X=\downarrow X$. $X\subseteq P$ jest zbiorem górnym, jeśli $X=\uparrow X$. $X\subseteq P$ jest ideałem, jeśli jest skierowany i dolny. $X\subseteq P$ jest filtrem, jeśli jest filtrowany i górny. Ideałem głównym nazywamy każdy ideał postaci $\downarrow x$ dla $x\in P$. Filtrem głównym jest każdy filtr postaci $\uparrow x$ dla pewnego $x\in P$.

Poset $P$ nazywamy dcpo) (od angielskiego określenia: directed-complete partial order), jeśli każdy zbiór skierowany posiada supremum w $P$.

W każdym zbiorze częściowo uporządkowanym $P$ możemy zdefiniować relację aproksymacji (ang. way-below relation) w następujący sposób: dla $x,y\in P$ mamy $x\ll y$ (czytamy: $x$ aproksymuje $y$ lub $x$ jest skończony względem $y$) wtedy i tylko wtedy, gdy dla każdego zbioru skierowanego $D{\subseteq }^{\uparrow }P$ takiego, że $y⊑{\bigvee }^{\uparrow }D$ mamy $x⊑d$ dla pewnego $d\in D$. W jednym zdaniu:

$x\ll y⟺\mathrm{\forall }D{\subseteq }^{\uparrow }P(y⊑\bigvee {}^{\uparrow }D\Rightarrow (\mathrm{\exists }d\in D(x⊑d)))$

Element $x\in P$ nazywamy zwartym lub skończonym, gdy $x\ll x$. Zbiór wszystkich elementów zwartych posetu $P$ oznaczamy zwykle $K(P)$. Dla relacji $\ll$ przyjmujemy podobne oznaczenia, jak dla porządku:

$\Downarrow X=\{z\in P\mid \mathrm{\exists }x\in X\mid z\ll x\}$

$\Uparrow X=\{w\in P\mid \mathrm{\exists }x\in X\mid x\ll w\}$

$\Downarrow x=\Downarrow \{x\}$

$\Uparrow x=\Uparrow \{x\}$

Relacja aproksymacji w dowolnym posecie $P$ posiada następujące własności:

• $(\mathrm{\forall }x,y\in P)(x\ll y\Rightarrow x⊑y)$,
• $(\mathrm{\forall }x,y,z,w\in P)(x⊑y\ll z⊑w\Rightarrow x\ll w)$,
• $(\mathrm{\perp }\in P\Rightarrow (\mathrm{\forall }x\in P(\mathrm{\perp }\ll x)))$.

Bazą posetu $P$ nazywamy każdy podzbiór $B$ taki, że dla każdego $x\in P$ zbiór $\Downarrow x\cap B$ jest skierowany i posiada supremum $x$.

Definicja 12.1

Poset $P$ jest ciągły jeśli posiada bazę. Jeśli $K(P)$ jest bazą, to mówimy, że $P$ jest algebraiczny.

Twierdzenie 12.2

Poset $P$ jest ciągły wtedy i tylko wtedy, gdy dla każdego $x\in P$, zbiór $\Downarrow x$ jest skierowany i mamy $x=\bigvee {}^{\downarrow }\Downarrow x$.

Dowód

Niech $P$ będzie ciągły i $B$ będzie bazą dla $P$. Niech $x\in P$ będzie dowolnym elementem $P$. Pokażemy, że $\Downarrow x$ jest zbiorem skierowanym i jego supremum to $x$. Niech $a,b\ll x$. Skoro z założenia zbiór $\Downarrow x\cap B$ jest skierowany z supremum $x$, to z definicji relacji aproksymacji istnieją dwa elementy $a^{\prime },b^{\prime }\in B$ takie, że $a⊑a^{\prime }\ll x$ oraz $b⊑b^{\prime }\ll x$. Ale ze skierowania zbioru $\Downarrow x\cap B$ wynika istnienie elementu $c\in B$ takiego, że $a^{\prime }⊑c\ll x$ oraz $b^{\prime }⊑c\ll x$. A zatem z własności (w2) mamy $a,b⊑c\ll x$, czyli wykazaliśmy, że zbiór $\Downarrow x$ jest skierowany. Zauważmy, że $x$ jest ograniczeniem górnym zbioru $\Downarrow x$. Jeśli $z\in P$ jest dowolnym innym ograniczeniem górnym, to skoro $\Downarrow x\cap B\subseteq \Downarrow x$, to $x=\bigvee {}^{\downarrow }(\Downarrow x\cap B)⊑z$. A zatem $x=\bigvee {}^{\downarrow }\Downarrow x$. Z drugiej strony, jeśli $P$ jest dowolnym posetem takim, że $x=\bigvee {}^{\downarrow }\Downarrow x$, to $P$ jest bazą, a więc $P$ jest ciągły.

Zauważmy, że drobna modyfikacja pierwszej części powyższego dowodu pozwala nam wywnioskować, że jeśli $B$ jest bazą dla $P$, to dowolny nadzbiór $B$ jest również bazą dla $P$.

Twierdzenie 12.3 [interpolatywność aproksymacji]

Jeśli poset jest ciągły, to relacja aproksymacji posiada własność interpolacji:

• $(\mathrm{\forall }M{\subseteq }_{fin}P)(\mathrm{\forall }x\in P)(M\ll x\Rightarrow (\mathrm{\exists }y\in P(M\ll y\ll x)))$.

Definicja 12.4 [dziedzina]

Poset $P$ nazywamy dziedziną lub dziedziną ciągłą, jeśli jest ciągłym dcpo.

Dziedziną algebraiczną nazywamy każdy dcpo algebraiczny $P$. Poset $P$ jest dziedziną $\omega$-ciągłą, jeśli posiada przeliczalną bazę. Dziedzina algebraiczna z przeliczalną bazą jest nazywana dziedziną $\omega$-algebraiczną lub dziedziną Scotta. (Zauważmy, że na to, by dziedzina algebraiczna $P$ była $\omega$-algebraiczna potrzeba i wystarcza, by baza $K(P)$ była przeliczalna. Dowód tego stwierdzenia jest bardzo prosty i wynika z dwóch faktów: z tego, że $K(P)\subseteq B$ dla każdej bazy $B$ dziedziny $P$ oraz z tego, że w dowolnym posecie każdy nadzbiór bazy jest również bazą).

Rozważmy następujące sztandarowe przykłady zbiorów częściowo uporządkowanych:

Przykład 12.5 [poset skończony]

Każdy poset skończony $P$ jest dcpo, ponieważ każdy jego podzbiór skierowany posiada element największy. Co więcej, każdy element $P$ jest zwarty, a więc $P$ jest dziedziną Scotta.

Przykład 12.6 [liczby naturalne]

W posecie liczb naturalnych $\omega$ z porządkiem naturalnym każdy element jest zwarty, tak więc $\omega$ jest posetem algebraicznym. Poset $\omega$ nie jest jednak dcpo, ponieważ łańcuch $\omega$ nie ma supremum.

Przykład 12.7 [odcinek]

Odcinek $[0,1]$ z naturalnym porządkiem jest ciągły, co łatwo wynika z faktu, że $x\ll y$ wtedy i tylko wtedy, gdy $x<y$ lub $x=0$. Jest to również krata zupełna, a więc w szczególności dziedzina ciągła i poset $bc$-zupełny.

Przykład 12.8 [zbiór potęgowy]

Niech $X$ będzie dowolnym zbiorem. Zbiór potęgowy ${𝒫}(X)$ jest kratą zupełną i dla każdego $Y\subseteq X$ mamy $\bigvee Y=\bigcup Y$ i $\bigwedge Y=\bigcap Y$. ${𝒫}(X)$ jest więc w szczególności dcpo i $bc$-zupełny. Najmniejszym elementem ${𝒫}(X)$ jest $\mathrm{\varnothing }$, a największym $X$.

Pokażemy, że dla $A,B\subseteq X$ mamy $A\ll B$ wtedy i tylko wtedy, gdy $A$ jest skończonym podzbiorem $B$. Rzeczywiście, załóżmy, że $A\ll B$. Ponieważ

$B=\bigcup \{F\subseteq X\mid F{\subseteq }_{fin}B\}$

i tenże zbiór jest skierowany, istnieje $F{\subseteq }_{fin}B$ taki, że $A\subseteq F$. Zbiór $A$ jest więc skończony, jako podzbiór zbioru skończonego $F$.

Załóżmy, że $A{\subseteq }_{fin}B$. Przypuśćmy, że $B\subseteq \bigcup {𝒟}$ dla pewnego zbioru skierowanego ${𝒟}$ w ${𝒫}(X)$. Mamy więc $A\subseteq \bigcup {𝒟}$, co oznacza, że dla każdego $a\in A$ istnieje $D_a\in {𝒟}$ taki, że $a\in D_a$. Ponieważ ${𝒟}$ jest skierowany, istnieje $D\in {𝒟}$, który zawiera wszystkie zbiory $D_a$. To oznacza, że $A\subseteq D\in {𝒟}$, co należało pokazać.

Przykład 12.9 [dziedzina podprzedziałów odcinka]

Niech $\mathbf{𝐈}[0,1]$ oznacza zbiór wszystkich podprzedziałów domkniętych, niepustych przedziału $[0,1]$ uporządkowany względem odwrotnej inkluzji, to znaczy: $[a,b]⊑[c,d]⟺[a,b]\supseteq [c,d]$

dla $a,b,c,d\in [0,1]$. Poset $\mathbf{𝐈}[0,1]$ jest dcpo, $bc$-zupełny, $\omega$-ciągły i nie jest algebraiczny. Elementem najmniejszym jest $[0,1]$, a element największy nie istnieje. Elementami maksymalnymi są wszystkie przedziały postaci $[a,a]$ dla $a\in [0,1]$, które utożsamiamy w sposób naturalny z liczbami rzeczywistymi z odcinka $[0,1]$. Relacja aproksymacji jest dana jako:

$[a,b]\ll [c,d]⟺[a,b]\supseteq (c,d)$

Bazą przeliczalną w $\mathbf{𝐈}[0,1]$ jest rodzina wszystkich podprzedziałów odcinka $[0,1]$ o końcach wymiernych.

Przykład 12.10 [dziedzina przedziałów]

Zbiór wszystkich domkniętych, niepustych przedziałów osi liczb rzeczywistych uporządkowany względem odwrotnej inkluzji, z dodanym elementem najmniejszym, oznaczamy $\mathbf{𝐈}\mathbb{ℝ}$. Poset $\mathbf{𝐈}\mathbb{ℝ}$ jest izomorficzny z $\mathbf{𝐈}[0,1]$, więc posiada dokładnie te same cechy co $\mathbf{𝐈}[0,1]$.

Przykład 12.11 [dziedzina kul]

Niech $(X,d)$ będzie przestrzenią metryczną. Rozważmy rodzinę wszystkich par postaci $(x,r)$, gdzie $x\in X$ i $r>0$ i zdefiniujmy relację $⊑$ w następujący sposób: $(x,r)⊑(y,s)⟺d(x,y)\le r-s$

Można pokazać, że relacja $⊑$ jest częściowym porządkiem. Poset

$\mathbf{𝐁}X=(\{(x,r)\mid x\in X,r>0\},⊑)$

jest ciągły, a relacja aproksymacji może być opisana jako:

$(x,r)\ll (y,s)⟺d(x,y)<r-s$

Poset $\mathbf{𝐁}X$ jest dziedziną (tj. jest dcpo) wtedy i tylko wtedy, gdy $X$ jest przestrzenią metryczną zupełną. Poset $\mathbf{𝐁}X$ jest $\omega$-ciągły wtedy i tylko wtedy, gdy przestrzeń metryczna $X$ jest ośrodkowa.

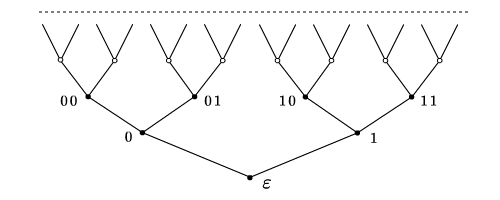
Przykład 12.12 [model zbioru Cantora]

Zbiór wszystkich skończonych i nieskończonych ciągów zerojedynkowych ${\mathrm{\Sigma }}^{\mathrm{\infty }}$ (oczywiście $\mathrm{\Sigma }=\{0,1\}$) w porządku prefiksowym jest dziedziną Scotta. Każdy zbiór skierowany jest łańcuchem. Elementem najmniejszym jest ciąg pusty $\epsilon$. Zbiór elementów maksymalnych pokrywa się ze zbiorem wszystkich ciągów nieskończonych, który z kolei, jak wiadomo, posiada strukturę zbioru Cantora. Każdy element z ${\mathrm{\Sigma }}^{\mathrm{\infty }}$, który nie jest maksymalny, jest zwarty.

Funkcje monotoniczne

Funkcję $f:P\to Q$ między posetami nazywamy monotoniczną, jeśli zachowuje porządek, tj. jeśli $x⊑y$ w $P$, to $f(x)⊑f(y)$ w $Q$. Funkcja $f$ jest ciągła, jeśli zachowuje suprema zbiorów skierowanych, to znaczy: jeśli $D\subseteq P$ jest skierowany i posiada supremum $\bigvee {}^{\downarrow }D\in P$, to $f[D]$ posiada supremum $\bigvee f[D]=f(\bigvee {}^{\downarrow }D)$. Zauważmy, że każda funkcja ciągła jest monotoniczna. Rzeczywiście, jeśli $x⊑y$ w $P$, to zbiór $\{x,y\}$ jest skierowany i ma supremum $y$. Tak więc $f(y)=f(x\vee y)=\bigvee \{f(x),f(y)\}=f(x)\vee f(y)⊒f(x)$. Z kolei, monotoniczność $f$ implikuje, że dla $D$ skierowanego, zbiór $f[D]$ jest również skierowany. Wnioskujemy więc, że funkcja $f$ jest ciągła wtedy i tylko wtedy, gdy dla dowolnego zbioru skierowanego $D$ posiadającego supremum, zbiór $f[D]$ jest skierowany oraz zachodzi $\bigvee {}^{\downarrow }f[D]=f(\bigvee {}^{\downarrow }D)$.

Uwaga

Jeśli funkcja monotoniczna $f:D\to E$ jest traktowana kategoryjnie, jako funktor między kategoriami $D$ i $E$, to pojęcie ciągłości, które tu wprowadziliśmy nie zgadza się z definicją ciągłości funktora. Przyjmijmy jednak, że w tym i dwóch następnych wykładach ciągłość funkcji między posetami będzie oznaczać tylko i wyłącznie zachowywanie supremów skierowanych.

Dziedziny jako topologie

Topologią na zbiorze $X$ nazywamy dowolną rodzinę $\tau$ podzbiorów zbioru $X$ zamkniętą zewzględu na skończone przecięcia i dowolne sumy, a parę $(X,\tau )$ nazywamy przestrzenią topologiczną.Definicję powyższą możemy wypowiedzieć na wiele równoważnych sposobów, na przykład: topologią nazywamy każdy podzbiór $\tau$ porządku $({𝒫}(X),\subseteq )$ zamknięty ze względu na dowolne suprema i skończone infima. O elementach $\tau$ mówimy, że są to zbiory otwarte. Z definicji mamy więc, że skończone przecięcie zbiorów otwartych jest zbiorem otwartym i dowolna suma zbiorów otwartych jest zbiorem otwartym. Tak więc rodzina $\mathrm{\Omega }(X)=(\tau ,\subseteq )$ jest kratą, w której istnieją wszystkie suprema. To znaczy, że $\mathrm{\Omega }(X)$ jest w rzeczywistości kratą zupełną, ponieważ infimum dowolnego podzbioru ${ℳ}$ zbioru $\tau$ jest równe supremum zbioru wszystkich ograniczeń dolnych ${ℳ}$. W szczególności, każda topologia na zbiorze $X$ zawiera zbiór pusty (który jest równy $\bigvee {ℳ}$ dla ${ℳ}=\mathrm{\varnothing }$) i całą przestrzeń $X$ ($=\bigwedge \mathrm{\varnothing }$).

Jeśli $\tau ={𝒫}(X)$, to $\tau$ nazywamy topologią dyskretną; jeśli $\tau =\{\mathrm{\varnothing },X\}$, to $\tau$ nazywamy topologią trywialną}.

Niech $(X,\tau )$ będzie przestrzenią topologiczną. Otoczeniempunktu $x\in X$ nazywamy dowolny zbiór $A$ taki, że $x\in U\subseteq A$ dla pewnego $U\in \tau$. Można łatwo pokazać, że dowolny podzbiór $B$ zbioru $X$ jest otwarty (to znaczy $B\in \tau$) wtedy i tylko wtedy, gdy $B$ jest otoczeniem każdego swojego elementu. Zbiór otoczeń $x\in X$ oznaczymy ${𝒩}(x)$. Jak łatwo zauważyć, zbiór ${𝒩}(x)$ jest filtrem w kracie $({𝒫}(X),\subseteq )$ i dlatego nazywamy go często filtrem otoczeń punktu $x$. Zauważmy też, że dla dowolnego $x\in X$, filtr otoczeń ${𝒩}(x)$ jest wyznaczony jednoznacznie, a więc w rzeczywistości odwzorowanie ${𝒩}:X\to {𝒫}({𝒫}(X))$ dane przez

$x\mapsto \{A\subseteq X\mid (\mathrm{\exists }U\in \tau )(x\in U\subseteq A)\}$

jest dobrze określoną funkcją.

Niech $(X,\tau )$ będzie przestrzenią topologiczną i niech $A\subseteq X$. Wnętrzem zbioru $A$ nazywamy największy zbiór otwarty zawarty w $A$, który będziemy oznaczać dalej jako ${\mathbf{𝐢}\mathbf{𝐧}\mathbf{𝐭}}_{\tau }(A)$ lub po prostu $\mathbf{𝐢}\mathbf{𝐧}\mathbf{𝐭}(A)$, jeśli jest jasne o jakiej topologii $\tau$ jest właśnie mowa. Zauważmy, że odwzorowanie $\mathbf{𝐢}\mathbf{𝐧}\mathbf{𝐭}:{𝒫}(X)\to {𝒫}(X)$ dane przez

$A\mapsto \bigcup \{O\mid O\subseteq A\}$

jest dobrze określoną funkcją. Ponadto, zbiór $O\subseteq X$ jest otwarty wtedy i tylko wtedy, gdy $O=\mathbf{𝐢}\mathbf{𝐧}\mathbf{𝐭}(O)$, to znaczy, gdy $O$ jest punktem stałym odwzorowania $\mathbf{𝐢}\mathbf{𝐧}\mathbf{𝐭}:{𝒫}(X)\to {𝒫}(X)$. Co więcej, $\tau =\{\mathbf{𝐢}\mathbf{𝐧}\mathbf{𝐭}(A)\mid A\subseteq X\}$.

Dopełnienia zbiorów otwartych w przestrzeni topologicznej nazywamy zbiorami domkniętymi. Rodzina zbiorów domkniętych posiada własności dualne do własności zbiorów otwartych, a więc jest zamknięta ze względu na dowolne przecięcia i skończone sumy i tworzy kratę zupełną, zarówno względem inkluzji, jak i względem odwrotnej inkluzji. Kratę zbiorów domkniętych oznaczamy dalej jako $\mathrm{\Gamma }(X)$. Ponieważ $\mathrm{\Gamma }(X)$ jest podzbiorem ${𝒫}(X)$ zamkniętym ze względu na dowolne infima, więc dla dowolnego $A\subseteq X$ istnieje najmniejszy zbiór domknięty zawierający $A$, który jest niczym innym, jak tylko infimum zbioru ograniczeń górnych $A$ w $\mathrm{\Gamma }(X)$ (czyli przecięciem wszystkich domkniętych nadzbiorów $A$). Zbiór ten oznaczamy ${\mathbf{𝐜}\mathbf{𝐥}}_{\tau }(A)$ albo po prostu $\mathbf{𝐜}\mathbf{𝐥}(A)$, jeśli $\tau$ jest ustalona. Podobnie, jak w przypadku operacji wnętrza, odwzorowanie $\mathbf{𝐜}\mathbf{𝐥}:{𝒫}(X)\to {𝒫}(X)$ jest dobrze określoną funkcją, a zbiór $C\subseteq X$ jest domknięty wtedy i tylko wtedy, gdy jest punktem stałym odwzorowania $\mathbf{𝐜}\mathbf{𝐥}$, to jest, gdy $C=\mathbf{𝐜}\mathbf{𝐥}(C)$.

Bazy w przestrzeniach topologicznych

Niech $(X,\tau )$ będzie przestrzenią topologiczną. Bazątopologii $\tau$ nazywamy każdą podrodzinę $\beta \subseteq \tau$ taką, że dla każdego otoczenia $A$ punktu $x$ istnieje $B\in \beta$ taki, że $x\in B\subseteq A$. W szczególności, cała rodzina $\tau$ jest bazą topologii $\tau$.

Przypomnijmy, że jeśli $P$ jest częściowym porządkiem, to jego podzbiory $A,B$ są współkońcowe, jeśli $\downarrow A=\downarrow B$. Ponadto, jeśli $A\subseteq B$ oraz $\downarrow A=\downarrow B$, to mówimy, że $A$ jest współkońcowy w $B$. Rozważmy więc kratę $({𝒫}(X),\supseteq )$ dla przestrzeni topologicznej $(X,\tau )$. W tej kracie rodzina ${𝒩}(x)$ dla dowolnego $x\in X$ jest zbiorem skierowanym. Zauważmy, że podrodzina $\beta$ topologii $\tau$ na $X$ jest bazą wtedy i tylko wtedy, gdy dla każdego $x\in X$, zbiór $\beta (x)$ jest współkońcowy w ${𝒩}(X)$, gdzie $\beta (x)=\{B\in \beta \mid x\in B\}$.

Zbiory zwarte

Podzbiór $K$ przestrzeni topologicznej $(X,\tau )$ nazywamy zwartym, jeśli dowolne pokrycie $K$ zbiorami otwartymi zawiera podpokrycie skończone, to jest: jeśli $K\subseteq \bigcup {ℳ}$ dla dowolnej rodziny ${ℳ}\subseteq \tau$, to istnieje podrodzina ${ℱ}{\subseteq }_{fin}{ℳ}$ taka, że $K\subseteq \bigcup {ℱ}$. W praktyce będziemy mieli bardzo często do czynienia z rodzinami indeksowanymi, więc definicja zwartości upraszcza się do następującej: $K\subseteq X$ jest zwarty wtedy i tylko wtedy, gdy $K\subseteq \bigcup _{i\in I}{A}_i$ dla $A_i\in \tau$ implikuje $K\subseteq A_{i_1}\cup ...A_{i_n}$ dla $i_1,...,i_n\in I$, gdzie $n\in \omega$.

Porządek specjalizacji i aksjomaty oddzielania

W dowolnej przestrzeni topologicznej

$(X,\tau )$

możemy zdefiniować relację przechodnią i zwrotną między elementami

$x,y\in X$

w następujący sposób:

$x{⊑}_{\tau }y⟺(\mathrm{\forall }U\in \tau )(x\in U\Rightarrow y\in U)$      ()

którą nazywamy preporządkiem specjalizacji. Mówimy, że przestrzeń topologiczna

$X$

spełnia aksjomat oddzielania

$T_0$

(lub: jest przestrzenią

$T_0$

) jeśli

${⊑}_{\tau }$

jest częściowym porządkiem, to znaczy wtedy i tylko wtedy, gdy

${⊑}_{\tau }$

jest relacją antysymetryczną. Dalej, mówimy, że przestrzeń topologiczna

$X$

spełnia aksjomat oddzielania

$T_1$

(jest przestrzenią

$T_1$

) wtedy i tylko wtedy, gdy

${⊑}_{\tau }$

redukuje się do równości. Oczywiście definicje powyższe implikują, że każda przestrzeń

$T_1$

jest

$T_0$

, ale nie jest odwrotnie, jak pokazuje przykład topologii

$\{\mathrm{\varnothing },\{1\},\{0,1\}\}$

na zbiorze dwuelementowym

$\{0,1\}$

.

Nazwy aksjomaty oddzielania pochodzą stąd, że w przestrzeniach topologicznych o własnościach $T_0$ czy $T_1$ zbiory otwarte oddzielają punkty w odpowiedni sposób. W dalszej części wykładu będziemy mówić głównie o przestrzeniach $T_0$, które nie są przestrzeniami $T_1$ (konkretnie, tak zwana topologia Scotta na nietrywialnych dziedzinach posiada te własności, co wykażemy poniżej). Z drugiej strony, niemal wszystkie przestrzenie topologiczne rozważane w analizie, geometrii itd., itp. spełniają aksjomaty silniejsze niż $T_1$. Nasz wykład będzie więc różnił się znacznie od standardowego wykładu topologii ogólnej.

Funkcje ciągłe na dziedzinach

Można śmiało powiedzieć, że struktura topologiczna na zbiorach jest wprowadzana po to, aby w sposób ścisły móc mówić o ciągłości funkcji. Przedmiot Topologia jest więc przede wszystkim nauką o funkcjach ciągłych między przestrzeniami topologicznymi.

Definicja 12.13

Niech $(X,\tau ),(Y,\alpha )$ będą przestrzeniami topologicznymi. Mówimy, że funkcja $f:X\to Y$ jest ciągła wtedy i tylko wtedy, gdy dla każdego zbioru otwartego $A$ w $Y$, przeciwobraz $f^{-1}[A]$ jest otwarty w $X$ (tj. $(\mathrm{\forall }A\subseteq Y)(A\in \alpha \Rightarrow f^{-1}[A]\in \tau$)).

Dowodzi się w prosty sposób, że funkcja jest ciągła wtedy i tylko wtedy, gdy przeciwobraz dowolnego zbioru domkniętego jest domknięty.

Topologia Scotta na porządkach

W tej części wykładu pokażemy, że każdy zbiór częściowo uporządkowany może być traktowany jako przestrzeń topologiczna. Topologia, którą w naturalny sposób można zdefiniować na każdym posecie nazywa się topologią Scotta i pochodzi od nazwiska słynnego logika Dany S. Scotta (prof. Scott wykłada i bierze udział w konferencjach matematycznych i informatycznych do dziś).

Definicja 12.14

Niech $P$ będzie częściowym porządkiem. Zbiór $U$ nazywamy otwartym w sensie Scotta, jeśli spełnia dwa warunki:

• $U=\uparrow U$ ($U$ jest zbiorem górnym),
• Jeśli dla zbioru skierowanego $D{\subseteq }^{\uparrow }P$ mamy $\bigvee {}^{\downarrow }D\in U$, to istnieje element $d\in D$ taki, że $d\in U$.

O zbiorze $U\subseteq P$ mającym własność (S2) mówimy, że jest nieosiągalny przez suprema zbiorów skierowanych. Rodzinę zbiorów otwartych w sensie Scotta oznaczamy $\sigma (P)$ lub po prostu $\sigma$.

Twierdzenie 12.15

Niech $P$ będzie częściowym porządkiem. Zbiory otwarte w sensie Scotta tworzą topologię.

Dowód

Niech $O,U\in \sigma$. Pokażemy, że $O\cap U\in \sigma$. Jest oczywiste, że $O\cap U$ jest zbiorem górnym, więc pokażemy tylko własność (S2). Niech $D$ będzie dowolnym zbiorem skierowanym w $P$, który posiada supremum $x=\bigvee {}^{\downarrow }D\in P$. Jeśli $x\in O\cap U$, to $x\in O$ i $x\in U$, a więc istnieją elementy $o\in D\cap O$ i $u\in D\cap U$. Ale $D$ jest skierowany, więc istnieje $y\in D$ taki, że $o,u⊑y$. Ponieważ $O$ i $U$ są zbiorami górnymi, $y\in D\cap (O\cap U)$, co należało pokazać. Niech $A_i$ będzie dowolną rodziną zbiorów otwartych. Jest jasne, że $\bigcup _{i\in I}{A}_i$ jest zbiorem górnym. Następnie, jeśli $\bigvee {}^{\downarrow }D=x\in \bigcup _{i\in I}{A}_i$ dla $D{\subseteq }^{\uparrow }D$, to $x\in A_i$ dla pewnego $i\in I$. A zatem istnieje $d\in D$ taki, że $d\in A_i$. Element $d$ należy więc do $\bigcup _{i\in I}{A}_i$, a więc $D\cap \bigcup _{i\in I}{A}_i$, czego należało dowieść.

Można pokazać, że zbiór $C\subseteq P$ jest domknięty w sensie Scotta, jeśli jest zbiorem dolnym i zawiera wszystkie suprema swoich podzbiorów skierowanych (o tej drugiej własności mówimy, że zbiór domknięty w sensie Scotta jest zamknięty ze względu na suprema zbiorów skierowanych). Najprostszymi przykładami zbiorów domkniętych są ideały główne $\downarrow x$ dla $x\in P$.

Okazuje się, że porządek specjalizacji dla topologii Scotta na $P$ jest zawsze porządkiem częściowym, który pokrywa się z tym na $P$.

Twierdzenie 12.16

Niech $(P,⊑)$ będzie częściowym porządkiem. Dla dowolnych elementów $x,y\in P$ następujące warunki są równoważne:

• $x⊑y$,
• $x{⊑}_{\sigma }y$,
• $x\in \mathbf{𝐜}\mathbf{𝐥}(\{y\})$.

Co więcej, topologia Scotta jest $T_0$.

Dowód

(1)$\Rightarrow$(2) wynika z tego, że zbiory otwarte są górne. (2)$\Rightarrow$(3): przypuśćmy, że $x\notin \mathbf{𝐜}\mathbf{𝐥}(\{y\})$. Wówczas istnieje $C$ domknięty w sensie Scotta, taki, że $y\in C$ i $x\notin C$. A zatem dla zbioru otwartego $U=P\setminus C$ mamy $x\in U$ i $y\notin U$. To znaczy, że Parser nie mógł rozpoznać (nieznana funkcja „\nepod”): {\displaystyle x\nepod_{\sigma} y} , co należało pokazać (3)$\Rightarrow$(1): ponieważ ideał $\downarrow y$ jest domknięty w sensie Scotta i zawiera $y$, więc $\mathbf{𝐜}\mathbf{𝐥}(\{y\})\subseteq \downarrow y$, a zatem $x\in \downarrow y$. Własność $T_0$ wynika z równoważności (1) i (2) powyżej.

Topologia Scotta na dziedzinach

Niech $P$ będzie porządkiem ciągłym. Łatwo pokazać, że w topologii Scotta na $P$ mamy $\mathbf{𝐢}\mathbf{𝐧}\mathbf{𝐭}(\uparrow x)=\Uparrow x$ dla każdego $x\in P$. Lecz o tej sytuacji możemy powiedzieć nawet więcej:

Twierdzenie 12.17

Niech $P$ będzie porządkiem ciągłym, a $B$ jego bazą. Wówczas rodzina $\beta =\{\Uparrow x\mid x\in B\}$ jest bazą dla topologii Scotta.

Dowód

Wiemy już, że elementy $\beta$ są zbiorami otwartymi w sensie Scotta. Niech $x\in U$ dla dowolnego $x\in B$ i $U\in \sigma (P)$. Skoro $\Downarrow x\cap B$ jest skierowany z supremum $x$, to z otwartości $U$ wynika, że istnieje $d\in \Downarrow x\cap B\cap U$. A zatem $x\in \Uparrow d\subseteq U$ dla pewnego $d\in B$, co należało pokazać.

Funkcje ciągłe w sensie Scotta

Na zakończenie pokażemy, że funkcje ciągłe między posetami są dokładnie funkcjami ciągłymi w sensie Scotta. Jest to jedna z przyczyn, dla których topologia Scotta odgrywa podstawową rolę w teorii dziedzin.

Twierdzenie 12.18

Niech $P,Q$ będą posetami. Dla funkcji $f:P\to Q$ następujące warunki są równoważne:

• $f$ jest ciągła,
• $f$ jest funkcją ciągłą między topologiami $(P,\sigma (P))$ i $(Q,\sigma (Q))$.

Dowód

Niech $f$ będzie ciągła i $O\in \sigma (Q)$. Ponieważ funkcje ciągłe są monotoniczne, $f^{-1}[O]$ jest zbiorem górnym. Jeśli $x=\bigvee {}^{\downarrow }D\in f^{-1}[O]$ dla pewnego zbioru skierowanego $D$, to $f(x)\in O$, to istnieje $d\in D$ taki, że $f(d)\in O$. To oznacza, że $d\in D\cap f^{-1}[O]$, co należało pokazać. Z drugiej strony, załóżmy, że $f$ jest ciągła w sensie Scotta. Niech $x⊑y$ w $P$. Wtedy $f^{-1}[\downarrow f(y)]$ jest zbiorem domkniętym w sensie Scotta zawierającym $y$, a więc zbiór ten musi zawierać również $x$. To daje $f(x)⊑f(y)$. Funkcja $f$ jest więc monotoniczna. Niech $D\subseteq P$ będzie skierowany. Rozważmy przeciwobraz zbioru domkniętego $\downarrow (\bigvee {}^{\downarrow }f[D])$. Jest on domknięty w $P$ i zawiera $D$, a więc musi też zawierać $\bigvee {}^{\downarrow }D$. Pokazaliśmy, że $f(\bigvee {}^{\downarrow }D)\in \downarrow (\bigvee {}^{\downarrow }f[D])$, czyli $f(\bigvee {}^{\downarrow }D)⊑\bigvee {}^{\downarrow }f[D]$. Ale monotoniczność $f$ implikuje, że $\bigvee {}^{\downarrow }f[D]⊑f(\bigvee {}^{\downarrow }D)$, co należało pokazać.