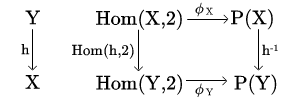Teoria kategorii dla informatyków/Ćwiczenia 5: Funktory i transformacje naturalne

==Zadanie 5.1==

Udowodnij, że transformacja naturalna $η$ funktorów typu $𝐂 \to 𝐃$ jest naturalnym izomorfizmem wtedy i tylko wtedy, gdy jest izomorfizmem w kategorii $F u n (𝐂, 𝐃)$ .

Wskazówka:

Rozwiązanie:

Niech $η$ będzie naturalnym izomorfizmem funktorów $F, G : 𝐂 \to 𝐃$ . Wtedy strzałka $η_{A} : F A \to G A$ jest z definicji izomorfizmem dla każdego $A \in 𝐂_{0}$ . Skoro tak, to każda taka strzałka posiada odwrotność $η_{A}^{- 1} : G A \to F A$ :

η_{A} \circ η_{A}^{- 1} = 1_{G A} o r a z η_{A}^{- 1} \circ η_{A} = 1_{F A}

Pokażemy, że $η_{A}^{- 1}$ jest transformacją naturalną typu $G \to F$ . Rzeczywiście, dla $f : A \to B$ , skoro $η_{A}$ jest naturalna: $G f \circ η_{A} = η_{B} \circ F f$ , a zatem $G f = η_{B} \circ F f \circ η_{A}^{- 1}$ , co z kolei pociąga: $η_{B}^{- 1} \circ G f = F f \circ η_{A}^{- 1}$ , co należało pokazać.

Odwrotnie, załóżmy że $F ≅ G$ . To znaczy, że istnieją dwie transformacje naturalne $η : F \to G$ oraz $ε : G \to F$ , takie że $η \circ ε = 1_{G}$ i $ε \circ η = 1_{F}$ . Z definicji złożenia transformacji naturalnych i definicji identyczności mamy natychmiast: $η_{A} \circ ε_{A} = 1_{G A}$ oraz $ε_{A} \circ η_{A} = 1_{F A}$ dla dowolnego $A \in 𝐂_{0}$ . To kończy dowód.

==Zadanie 5.2==

Udowodnij, że funktor inkluzji $𝐏 𝐨 𝐬 \to 𝐂 𝐚 𝐭$ zachowuje strukturę kategorii kartezjańsko zamkniętej, zaś funktor inkluzji $𝐆 𝐫 𝐩 \to 𝐂 𝐚 𝐭$ tej struktury nie zachowuje w ogólności.

Wskazówka:

Rozwiązanie:

W pierwszej części zadania funktor inkluzji $I$ działa tak, że poset $(P, \leq)$ traktuje jako kategorię, zaś funkcję monotoniczną $f : (P, \leq) \to (Q, \leq)$ jako funktor. Czy ta definicja jest dobrze postawiona? Tak, trywialnie tak, ponieważ zachowywanie identyczności przez $f$ sprowadza się do implikacji (dla $p, q, r \in P$ ): $p \leq p \Rightarrow f (p) \leq f (p)$ , zaś zachowanie złożenia do implikacji $p \leq q \leq r \Rightarrow f (p) \leq f (q) \leq f (r)$ , co jest równoważne monotoniczności $f$ . Wniosek: funktory między kategoriami $(P, \leq)$ i $(Q, \leq)$ to dokładnie funkcje monotoniczne. Wniosek drugi: $I$ jest dobrze zdefiniowany.

Czym są zatem transformacja naturalna $η : f \to g$ , gdzie $f, g : P \to Q$ są funktorami? Dla każdego $p \in P$ musimy mieć komponent: $η_{P} : f p \leq g p$ , zaś naturalność oznacza, że musimy mieć komutujący diagram, w którym $f p \leq f q$ i $g p \leq g q$ dla $p, q \in P$ , co jest zawsze spełnione. A zatem jedynym warunkiem, aby $η$ była transformacją naturalną jest to, że w posecie $Q^{P} (= F u n (P, Q))$ mamy $η : f \to q$ wtedy i tylko wtedy, gdy dla każdego $p \in P$ , $f p \leq g p$ , co oznacza, że porządek na $Q^{P}$ jest po współrzędnych. To jednak wystarcza, by powiedzieć, że $Q^{P}$ jest eksponentem $P$ i $Q$ w $𝐏 𝐨 𝐬$ , tzn. $Q^{P} = [P, Q]$ . Ostatnie zdanie mówi dokładnie tyle, że $I$ zachowuje eksponent, a to chcieliśmy wykazać. (Zachowanie obiektu końcowego i produktów w $𝐏 𝐨 𝐬$ pokazuje się tak samo.)

Zajmijmy się teraz kategorią grup $𝐆 𝐫 𝐩$ . Naszkicujemy dowód, że inkluzja $I : 𝐆 𝐫 𝐩 \to 𝐂 𝐚 𝐭$ nie zachowuje eksponentu. Dzieje się tak, ponieważ $H^{G}$ dla grup $G$ , $H$ nie jest zwykle grupą (często posiada więcej niż jeden obiekt - a przypomnijmy sobie, że grupą nazywamy kategorię, która ma dokładnie jeden obiekt i w której każdy morfizm jest izomorfizmem), tzn. może być w ogólności wiele homomorfizmów grup typu $G \to H$ .

==Zadanie 5.3==

Niech $𝐀, 𝐁, 𝐂$ będą kategoriami. Udowodnić, że operacja $F : 𝐀 \times 𝐁 \to 𝐂$ zdefiniowana na obiektach i strzałkach jest funktorem wtedy i tylko wtedy, gdy:

$F$ jest funktorem ze względu na każdy z argumentów osobno, tzn. dla każdego $A \in 𝐀_{0}$ , $F (A, -) : 𝐁 \to 𝐂$ jest funktorem i dla każdego $B \in 𝐁_{0}$ , $F (-, B) : 𝐀 \to 𝐂$ jest funktorem oraz:
$F$ spełnia następujące prawo przemienności:

dla dowolnych $f : A \to A^{'} \in 𝐀_{1}$ , $g : B \to B^{'} \in 𝐁_{1}$ .

Rozwiązanie:

Jeśli $F$ jest funktorem, to ponieważ dla każdej strzałki w $𝐀 \times 𝐁$

(f, g) : (A, B) \to (A^{'}, B^{'})

mamy

(f, 1_{B^{'}}) \circ (1_{A}, g) = (f \circ 1_{A}, 1_{B^{'}} \circ g) = (f, g) = (1_{A^{'}} \circ f, g \circ 1_{B}) = (1_{A^{'}}, g) \circ (f, 1_{B})

więc

F (f, 1_{B^{'}}) \circ F (1_{A}, g) = F (1_{A^{'}}, g) \circ F (f, 1_{B})

a zatem (1),(2) zachodzą. Odwrotnie, mając dane (1),(2), musimy pokazać, że operacja $F$ jest funktorem. Oczywiście definicje:

F ((A, B)) : = F (A, B) \in 𝐂_{0}

F ((f, g)) : = F (A^{'}, g) \circ F (f, B)

są dobrze postawione. Używając prawa przemienności, mamy dla $f : A \to A^{'}, f^{'} : A^{'} \to A^{″}, g : B \to B^{'}, g^{'} : B^{'} \to B^{″}$ :

Parser nie mógł rozpoznać (błąd składni): {\displaystyle F(f',g')\circ F(f,g) &=& (F(A'',g')\circ F(f,B'))\circ F(f,g)=(F(A'',g')\circ F(f,B'))\circ (F(A',g)\circ F(f,B))=F(A'',g')\circ (F(f,B')\circ F(A',g))\circ F(f,B)=F(A'',g')\circ (F(A'',B)\circ F(f',B))\circ F(f,B)=(F(A'',g')\circ F(A'',B))\circ (F(f',B)\circ F(f,B))\\ &=& F((f',g')\circ(f,g))}

==Zadanie 5.4==

Zdefiniować produkt dwóch funktorów.

Wskazówka:

Rozwiązanie:

Jeśli $F : 𝐀 \to 𝐁$ i $G : 𝐂 \to 𝐃$ są funktorami między małymi kategoriami, to potraktujmy je jako strzałki w $𝐂 𝐚 𝐭$ . Wiemy już, że w dowolnej kategorii z produktami, a taką przecież jest $𝐂 𝐚 𝐭$ - patrz przykłady do Podrozdziału nt. produktów., produkt dwóch strzałek da się kanonicznie zdefiniować tak, by posiadał wymaganą własność uniwersalną (tj. był jedyną strzałką taką, że odpowiedni diagram komutuje). W naszym przypadku będzie to:

F \times G = (F \circ P_{𝐀}, G \circ P_{𝐂})

gdzie $P_{𝐀} : 𝐀 \times 𝐁 \to 𝐀$ i $P_{𝐂} : 𝐂 \times 𝐃 \to 𝐂$ są odpowiednimi funktorami-projekcjami. Sprawdzenie, że $F \times G$ jest rzeczywiście funktorem wynika wprost z definicji i jest polecane jako ćwiczenie tylko w ostateczności.

Na koniec wystarczy zauważyć, że jeśli kategorie $𝐀, 𝐁, 𝐂, 𝐃$ są dowolne (niekoniecznie małe), to powyższy dowód (kropka w kropkę) również działa.

==Zadanie 5.5==

Udowodnij, że operacja $𝒫 : {𝐒 𝐞 𝐭}^{o p} \to 𝐒 𝐞 𝐭$ :

A \mapsto 𝒫 (A)

f : A \to B \mapsto f^{- 1} : 𝒫 (B) \to 𝒫 (A)

jest funktorem. Udowodnij, że funktor ten jest naturalnie izomorfizczny z hom-funktorem ${H o m}_{𝐒 𝐞 𝐭} (-, 2)$ , gdzie $2 : = {0, 1}$ jest dowolnym zbiorem dwuelementowym.

Wskazówka:

Tenże funktor $𝒫 : {𝐒 𝐞 𝐭}^{o p} \to 𝐒 𝐞 𝐭$ jest znany jako kontrawariantny funktor potęgowy.

Rozwiązanie:

Sprawdzimy najpierw, że $𝒫$ zachowuje identyczności:

𝒫 (1_{X}) (Z \subseteq X) = 1^{- 1} [Z] = Z

co oznacza, że $𝒫 (1_{X}) = 1_{𝒫 (X)}$ . Zachowanie złożenia:

𝒫 (f \circ g) (Z) = (f \circ g)^{- 1} [Z] = g^{- 1} [f^{- 1} [Z]] = 𝒫 (g) (f^{- 1} [Z]) = (𝒫 (g) \circ 𝒫 (f)) (Z)

co daje $𝒫 (f \circ g) = 𝒫 (g) \circ 𝒫 (f)$ . A zatem $𝒫$ jest funktorem.

Sprawdzimy teraz, że izomorfizm $𝒫 ≅ {H o m}_{𝐒 𝐞 𝐭} (-, 2)$ jest zadany przez parę wzajemnie do siebie odwrotnych transformacji naturalnych $ϕ : {H o m}_{𝐒 𝐞 𝐭} (-, 2) \to 𝒫$ i $ψ : 𝒫 \to {H o m}_{𝐒 𝐞 𝐭} (-, 2)$ znanych nam powszechnie jako bijekcja między podzbiorami danego zbioru i funkcjami charakterystycznymi podzbiorów: dla $X \in {𝐒 𝐞 𝐭}_{0}$

ϕ_{X} : {H o m}_{𝐒 𝐞 𝐭} (X, 2) \to 𝒫 (X)

f \mapsto {x ∣ f (x) = 1}

oraz

ψ_{X} : 𝒫 (X) \to {H o m}_{𝐒 𝐞 𝐭} (X, 2)

$S \mapsto χ_{S} : = {\begin{cases} 1 & x \in S \\ 0 & x \notin S . \end{cases}$

Sprawdzenie, że $ϕ, ψ$ są transformacjami naturalnymi jest czynnością rutynową, na przykład dla $ϕ$ musimy pokazać, że poniższy diagram komutuje (dla dowolnej funkcji $h : Y \to X$ ):

co sprowadza się do obliczenia dla $f : X \to 2$ :

ϕ_{Y} (f \circ h) = h^{- 1} [ϕ_{X} (f)]

czyli pokazania równości zbiorów:

{z ∣ f (h (z)) = 1} = h^{- 1} [{w ∣ f (w) = 1}]

co jest oczywiście prawdą.

Dowód dla $ψ$ jest równie łatwy i pomijamy go. Na zakończenie pokażemy tylko, że każda ze strzałek $ϕ_{X}$ dla $X \in {𝐒 𝐞 𝐭}_{0}$ jest izomorfizmem z odwrotnością $ψ_{X}$ . Oto uzasadnienie:

(ϕ_{X} \circ ψ_{X}) (S) = ϕ_{X} (χ_{S}) = {z ∣ χ_{S} (z) = 1} = S

co daje $ϕ_{X} \circ ψ_{X} = 1_{𝒫 (X)}$ oraz:

(ψ_{X} \circ ϕ_{X}) (f : X \to 2) = ψ_{X} ({x ∣ f (x) = 1}) = χ_{{x ∣ f (x) = 1}} = f

co pokazuje $ψ_{X} \circ ϕ_{X} = 1_{{H o m}_{𝐒 𝐞 𝐭} (X, 2)}$ .

==Zadanie 5.6==

Udowodnij, że dla zbiorów $A, B, C$ istnieje następująca bijekcja pomiędzy zbiorami potęgowymi:

𝒫 (B + C) ≅ 𝒫 (B) \times 𝒫 (C)

Wskazówka:

Pokazać najpierw naturalną bijekcję dla zbiorów:

[B + C, A] ≅ [B, A] \times [C, A]

Rozwiązanie:

Zgodnie ze wskazówką pokazujemy, że dla dowolnego zbioru $Z$ mamy:

H o m (Z, [B + C, A]) ≅ H o m (Z \times (B + C), A) ≅ H o m ((Z \times B) + (Z \times C), A) ≅ H o m ((Z \times B), A) \times H o m (Z \times C, A) ≅ H o m ((Z \times B), A) \times H o m (Z \times C, A) ≅ H o m (Z, [B, A]) \times H o m (Z, [C, A])

i korzystając z techniki używanej już w zadaniach do Wykładu 4., uwierzytelnionej w Wykładzie 7., wnioskujemy, że $[B + C, A] ≅ [B, A] \times [C, A]$ . W szczególności, dla $A = 2 : = {0, 1}$ dostajemy $H o m (B + C, 2) ≅ H o m (B, 2) \times H o m (C, 2)$ (musimy zauważyć też, że w $𝐒 𝐞 𝐭$ eksponentem $[X, Y]$ jest zbiór wszystkich funkcji z $X$ do $Y$ , czyli $H o m (X, Y)$ ). Ponieważ jednak z poprzedniego zadania (Zadanie 5.5) wynika, że funktor $H o m (-, 2)$ jest w bijekcji z funktorem potęgowym $𝒫$ , istnieją bijekcje (patrz Zadanie 5.1.)

H o m (B + C, 2) ≅ 𝒫 (B + C)

H o m (B, 2) ≅ 𝒫 (B)

H o m (C, 2) ≅ 𝒫 (C)

które wraz z pokazanym już $H o m (B + C, 2) ≅ H o m (B, 2) \times H o m (C, 2)$ pozwala nam stwierdzić, że:

𝒫 (B + C) ≅ 𝒫 (B) \times 𝒫 (C)

==Zadanie 5.7==

Na dowolnym posecie $(P, \leq)$ zadajemy tzw. topologię Aleksandrowa, deklarując zbiory górne jako otwarte. Pokaż, że ta konstrukcja da się rozszerzyć do funktora typu $𝐏 𝐨 𝐬 \to 𝐓 𝐨 𝐩$ . Czy ten funktor jest pełny? Wierny?

Wskazówka:

Rozwiązanie:

Dla częściowego porządku $(P, \leq)$ topologię Aleksandrowa będziemy oznaczać jako $α (P)$ . Jeśli więc nasza konstrukcja nazywa się $I : 𝐏 𝐨 𝐬 \to 𝐓 𝐨 𝐩$ , to możemy napisać $I ((P l e q)) : = (P, α (P))$ . Aby operacja $I$ była funktorem, musi przede wszystkim posyłać każdą funkcję monotoniczną $f : (P, \leq) \to (Q, \leq)$ w pewną funkcję ciągłą $I (f) : (P, α (P)) \to (Q, α (Q))$ . Najprostszym możliwym rozwiązaniem jest przyjęcie $I (f) : = f$ , ale aby ta definicja była poprawna, musi być tak, że każda funkcja monotoniczna jest funkcją ciągłą między topologiami Aleksandrowa. Sprawdźmy, czy tak jest w istocie. Załóżmy zatem, że $f : (P, \leq) \to (Q, \leq)$ jest funkcją monotoniczną. Wystarczy pokazać, że przeciwobraz dowolnego zbioru górnego w $Q$ jest zbiorem górnym w $P$ . Niech zatem $U \subseteq Q$ będzie górny, niech $x \in f^{- 1} [U]$ oraz niech $x \leq y$ dla $x, y \in P$ . Z monotoniczności $f$ dostajemy: $f (x) \leq f (y)$ , zaś z założeń: $f (x) \in U$ - i co za tym idzie - $f (y) \in U$ , bo $U$ górny. Dlatego też $y \in f^{- 1} [U]$ , co dowodzi, że $f^{- 1} [U]$ jest górnym podzbiorem $P$ . Możemy więc bez obaw zdefiniować operację $I$ na strzałkach jako: I(f\colon (P,\leq)\to (Q,\leq)):= f\colon (P,\alpha(P))\to(Q,\alpha(Q)).

Operacja $I$ jest oczywiście funktorem - przy tak prostej definicji $I$ dowód jest trywialny. Na zakończenie zauważmy więc, że $I$ będzie funktorem pełnym i wiernym wtedy i tylko wtedy, gdy dowolna funkcja $P : P \to Q$ jest monotoniczna dokładnie wtedy, gdy jest ciągła względem topologii Aleksandrowa (pełność jest istotna; wierność przy tak prostej definicji $I$ trywializuje się). Ponieważ dowiedliśmy tej własności w jedną stronę, pozostaje nam implikacja odwrotna: załóżmy, że $f : P \to Q$ jest ciągła. Pokażemy, że jest monotoniczna. Niech $x \leq y$ w $P$ i rozważmy zbiór $A : = f^{- 1} [↑ f (x)]$ , który - jak wynika z założenia ciągłości - jest górnym podzbiorem $P$ . Oczywiście $x \in A$ , a skoro $A$ górny, również $y \in A$ . Dlatego $f (y) \in ↑ f (x)$ , co czytamy inaczej jako $f (x) \leq f (y)$ . To kończy uzasadnienie faktu, że $f$ jest monotoniczna, jak również dowód tego, że $I$ jest funktorem pełnym i wiernym.

==Zadanie 5.8==

Zdefiniuj funktor dualny do hom-funktora zaproponowanego w Przykładzie 5.7.

Rozwiązanie:

Hom-funktorem kowariantnym w lokalnie małej kategorii $𝐂$ będzie następująca operacja dla każdego $X \in 𝐂_{0}$ :

{H o m}_{𝐂} (X, -) : 𝐂 \to 𝐒 𝐞 𝐭

𝐂_{0} ∋ Y \mapsto {H o m}_{𝐂} (X, Y)

𝐂_{1} ∋ f : A \to B \mapsto {H o m}_{𝐂} (X, f) : {H o m}_{𝐂} (X, A) \to {H o m}_{𝐂} (X, B)

p : X \to A \mapsto f \circ p : X \to B

Pokażmy, że jest to funktor:

{H o m}_{𝐂} (X, 1_{Z}) (q) = 1_{Z} \circ q = q

{H o m}_{𝐂} (X, h \circ k) (q) = h \circ k \circ q = {H o m}_{𝐂} (X, h) (k \circ q) = ({H o m}_{𝐂} (X, h) \circ {H o m}_{𝐂} (X, k)) (q)

co kończy dowód.

Teoria kategorii dla informatyków/Ćwiczenia 5: Funktory i transformacje naturalne

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia