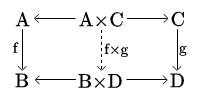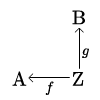Teoria kategorii dla informatyków/Ćwiczenia 3: Zasada dualności i proste konstrukcje uniwersalne

==Zadanie 3.1==

Kiedy w częściowym porządku $(P, \leq)$ istnieje produkt dwóch elementów $p, q \in P$ ?

Rozwiązanie:

Przypuśćmy, że $p \times q$ jest produktem $p$ i $q$ . Wówczas istnieją projekcje $p \times q \leq p$ i $p \times q \leq q$ , co świadczy o tym, że element $p \times q$ jest ograniczeniem dolnym zbioru ${p, q}$ . Własność uniwersalna produktu mówi, że dla dowolnego $z \in P$ , jeśli $z \leq p, q$ , to $z \leq p \times q$ , a zatem $p \times q$ jest infimum elementów $p$ i $q$ (największym ograniczeniem dolnym $p$ i $q$ ). Dualnie, koproduktem jest supremum. Jak widać, posety stanowią kategorie, gdzie produkt i koprodukt dowolnych dwóch elementów nie muszą istnieć. Poset z produktami i koproduktami dla każdej pary elementów nazywa się kratą.

==Zadanie 3.2==

Omówić koprodukt w $𝐒 𝐞 𝐭$ .

Rozwiązanie:

Na początku musimy zgadnąć, jakim zbiorem jest $A + B$ i funkcje $i_{A}, i_{B}$ . Intuicja podpowiada, że skoro koprodukt jest dualny do produktu, to $A + B$ może być sumą $A \cup B$ , zaś $i_{A}, i_{B}$ - zanurzeniami. Niestety, gdy wybierzemy $A = {a, b}$ , $B = {b, c}$ , $X = {a, b, b^{'}, c}$ oraz dwie funkcje $f : A \to X$ : $f (a) = a$ i $f (b) = b$ , $g : B \to X$ : $g (b) = b^{'}$ , $g (c) = c$ , to nie znajdziemy żadnej funkcji $h : A \cup B \to X$ takiej, że $f = h \circ i_{A}$ i $g = g \circ i_{B}$ . Widać, że to z tej przyczyny, iż iloczyn $A \cap B$ jest niepusty i element $b \in A \cap B$ jest albo posyłany w $b \in Z$ , albo w $b^{'} \in Z$ przez funkcje $f$ i $g$ . Żądajmy więc, aby suma zbiorów $A$ i $B$ była rozłączna! Po chwili zastanowienia okazuje się, że to dobry pomysł. Pokażmy zatem, że koproduktem zbiorów $A$ , $B$ jest suma rozłączna:

S : = {(a, 1) ∣ a \in A} \cup {(b, 2) ∣ b \in B}

wraz z zanurzeniami

i_{1} (a) : = (a, 1), i_{2} (b) : = (b, 2)

Jeśli dla dowolnych funkcji $f : A \to Z$ , $g : B \to Z$ zdefiniujemy:

[f, g] (x, n) : = {\begin{cases} f (x) & n = 1 \\ g (x) & n = 2, \end{cases}

to jeśli $h \circ i_{A} = f$ oraz $h \circ i_{B} = g$ dla $h : S \to Z$ , to $[f, g] (x, n) = (f (x) \lor g (x)) = (h i_{A} (x) \lor h i_{B} (x)) = h ((x, n))$ , czyli $[f, g] = h$ . To dowodzi, że $S = A + B$ , co należało pokazać.

==Zadanie 3.3==

Wykaż, że $(A \times B) \times C ≅ A \times (B \times C)$ dla $A, B, C \in 𝐂_{0}$ w dowolnej kategorii $𝐂$ , w której oba produkty istnieją. Jakie jest stwierdzenie dualne?

Rozwiązanie:

Rozważamy dwa diagramy, na których wszystkie nie nazwane strzałki są odpowiednimi projekcjami:

Wtedy funkcje $(p_{2}, p_{1}, f) : (A \times B) \times C \to A \times (B \times C)$ i $(g, p_{4} p_{3}) : A \times (B \times C) \to (A \times B) \times C$ składają się w obie strony do jedności (co łatwo sprawdzić, śledząc diagramy), a zatem są wzajemnie odwrotnymi izomorfizmami, co należało pokazać.

Zdanie dualne to oczywiście $(A + B) + C ≅ A + (B + C)$ , ponieważ $\times^{o p} = +$ oraz $≅^{o p} = ≅$ (tzn. izomorfizm jest pojęciem samodualnym).

==Zadanie 3.4==

Udowodnić, że jeśli w kategorii $𝐂$ istnieje obiekt końcowy i wszystkie pulbaki, to istnieją także produkty i ekwalizatory. Jak brzmi twierdzenie dualne?

Wskazówka:

Twierdzenie dualne brzmi: w kategorii $𝐂$ z obiektem początkowym, jeśli istnieją pushouty, to istnieją także koprodukty i koekwalizatory.

Rozwiązanie:

Niech $X, Y \in 𝐂_{0}$ . Rozważmy strzałki do obiektu końcowego:

X \overset{X}{⟶} 𝟏 \overset{Y}{⟵} Y

i niech

X \overset{p}{\leftarrow} P \overset{q}{\to} Y

będzie ich pulbakiem. Wówczas ten sam

X \overset{p}{\leftarrow} P \overset{q}{\to} Y

jest produktem $X$ i $Y$ . Rzeczywiście, złożenia $X \circ p$ i $Y \circ q$ są strzałkami, które posyłają $P$ w $𝟏$ . Ale strzałka w obiekt końcowy może być tylko jedna, więc $X \circ p = Y \circ q$ . Jeśli zaś weźmiemy dowolny inny obiekt $Q$ i strzałki $f : Q \to X$ , $g : Q \to Y$ , to mamy $X \circ f = Y \circ g$ z własności uniwersalnej $𝟏$ , a zatem z własności uniwersalnej pulbaku istnieje dokładnie jedna strzałka $h : Q \to P$ taka, że $p \circ h = q \circ h$ , co należało pokazać.

Weźmy teraz dwie równoległe strzałki $f, g : X \to Y$ . Tworzymy pulbak:

i wtedy $E \overset{e}{\to} X$ jest ekwalizatorem $f$ i $g$ . Szczegóły są tu równie łatwe jak w przypadku produktu.

==Zadanie 3.5==

Udowodnij, że w dowolnej lokalnie małej kategorii $𝐂$ hom-funktor $H o m (A, -) : 𝐂 \to 𝐒 𝐞 𝐭$ , gdzie $A \in 𝐂_{0}$ , zachowuje produkty.

Wskazówka:

Rozwiązanie:

Zdanie, które musimy wykazać, to:

H o m (A, B \times C) ≅ H o m (A, B) \times H o m (A, C)

a to w przypadku $𝐂 = 𝐒 𝐞 𝐭$ jest znany z teorii mnogości izomorfizm pomiędzy zbiorami wyznaczony przez funkcję:

A \overset{f}{\to} B \times C \mapsto (p_{B} \circ f, p_{C} \circ f)

gdzie $p_{B}, p_{C}$ są odpowiednimi projekcjami. Zwróćmy uwagę, że powyższa definicja da się wypowidzieć w przypadku dowolnej kategorii $𝐂$ . Jej postać jest uniwersalna i z definicji produktu natychmiast wynika, że strzałka ta jest szukanym izomorfizmem.

==Zadanie 3.6==

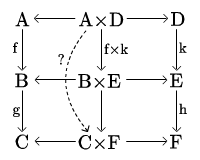
Widzieliśmy, że pulbak jest funktorem. Udowodnij, że produkt jest funktorem.

Wskazówka:

Niech $𝐂$ będzie dowolną kategorią z produktami. Musimy w pierwszej kolejności wskazać dwie operacje:

A, B \mapsto A \times B

f, g \mapsto f \times g

odpowiednio dla obiektów $A, B \in 𝐂_{0}$ i strzałek $f, g \in 𝐂_{1}$ . Tylko druga z nich wymaga zastanowienia. Proponujemy dla $f : A \to B$ , $g : C \to D$ , produkt $f \times g : A \times C \to B \times D$ jako jedyną strzałkę, dla której poniższy diagram komutuje:

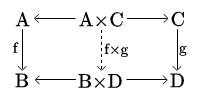
gdzie nie nazwane strzałki są projekcjami (jedyność $f \times g$ wynika z własności uniwersalnej produktu $B \times D$ ).

Rozwiązanie:

Pokażmy, że identyczności są zachowane, tzn. że $1_{A \times B} = 1_{A} \times 1_{B}$ . To proste: w poniższym komutującym diagramie w miejsce jedynej strzałki $?$ pasują zarówno $1_{A} \times 1_{B}$ , jak i $1_{A \times B}$ . A zatem muszą być równe.

Aby zakończyć dowód należy pokazać, że:

(g \circ f) \times (h \circ k) = (g \times h) \circ (f \times k)

co z kolei natychmiast wynika z komutowania poniższego diagramu (zwróćmy uwagę, że w miejsce jedynej strzałki $?$ pasuje zarówno $(g \circ f) \times (h \circ k)$ , jak i $(g \times h) \circ (f \times k)$ , co sprawia, że te strzałki muszą być równe.

==Zadanie 3.7==

Udowodnij, że produkt zachowuje izomorfizmy, tzn. jeśli $A ≅ A^{'}$ i $B ≅ B^{'}$ , to $A \times B ≅ A^{'} \times B^{'}$ .

Wskazówka:

Rozwiązanie:

Załóżmy, że mamy izomorfizmy: $g \circ f = 1_{A}$ , $f \circ g = 1_{A^{'}}$ , $h \circ k = 1_{B}$ , $k \circ h = 1_{B^{'}}$ . Wtedy

(f \times k) \circ (g \times h) = (f \circ g) \times (k \circ h) = 1_{A^{'}} \times 1_{B^{'}} = 1_{A^{'} \times B^{'}}

i analogicznie

(g \times h) \circ (f \times k) = (g \circ f) \times (h \circ k) = 1_{A} \times 1_{B} = 1_{A \times B}

Udowodniliśmy zatem, że $g \times h$ i $f \times k$ są wzajemnie odwrotnymi izomorfizmami.

==Zadanie 3.8==

Udowodnij Lemat Pulbakowy.

Rozwiązanie:

Udowodnimy tylko połowę lematu; drugą część rozwiązuje się w taki sam sposób - obserwując komutujące diagramy. Pokażemy zatem, że jeśli dwa wewnętrzne kwadraty są pulbakami, to zewnętrzny prostokąt też. Pracujemy na następującym diagramie:

Załóżmy: (1) $g y = g c x$ . Z prawego pulbaku istnieje dokładnie jedna strzałka $k$ taka, że: (2) $e k = y$ , oraz: (3) $c x = d k$ . Z lewego pulbaku, w świetle (3), istnieje dokładnie jedna strzałka $l$ taka, że: (4) $a l = k$ , oraz: (5) $b l = x$ . Z (5),(4),(2) wynika więc $e a l = e k = y$ , co kończy dowód.

==Zadanie 3.9==

Pokaż, że twierdzenie odwrotne do Faktu 3.7 nie zachodzi.

Wskazówka:

Szukamy takiej kategorii, w której istnieje monomorfizm, który nie jest ekwalizatorem żadnych dwóch równoległych strzałek tej kategorii. Poszukajmy takiego mono w monoidzie liczb naturalnych $(𝐍, +, 0)$ .

Rozwiązanie:

Wszystkie strzałki w $(𝐍, +, 0)$ są mono, w szczególności $1$ . Ale $1$ nie ekwalizuje żadnej pary $(m, n)$ . Gdyby tak było, to mielibyśmy $m + 1 = n + 1$ . Stąd $m = n$ i dalej: $m + 0 = n + 0$ . Z własności uniwersalnej, $0$ musiałoby się faktoryzować przez $1$ , czyli musiałaby istnieć taka liczba naturalna $k$ , że $1 + k = 0$ , sprzeczność.

==Zadanie 3.10==

Pokazać, że w $𝐒 𝐞 𝐭$ dowolny monomorfizm jest ekwalizatorem.

Wskazówka:

Dla funkcji $f : A \to B$ rozważamy dwie funkcje $B \to {0, 1}$ - funkcję charakterystyczną obrazu $I m (f)$ :

χ_{f} (b) : = {\begin{cases} 1, & dla b \in I m (f) \\ 0 & w przeciwnym przypadku . \end{cases}

i stałą funkcję $t t : B \to {0, 1}$ równą $1$ dla każdego $b \in B$ .

Rozwiązanie:

Pracujemy na następującym diagramie:

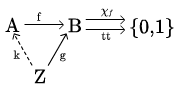
Oczywiście $(χ_{f} \circ f) (a) = χ_{f} (f (a)) = 1 = t t (f (a)) = (t t \circ f) (a)$ , czyli $χ_{f} \circ f = t t \circ f$ . Jeśli dla pewnego $g$ mamy $χ_{f} \circ g = t t \circ g$ , to $χ_{f} (g (z)) = 1$ , co oznacza, że $g (z) \in I m (f)$ , czyli istnieje $a_{z} \in A$ takie, że $g (z) = f (a_{z})$ . Wystarczy więc zdefiniować funkcję $k : Z \to A$ jako $k (z) : = a_{z}$ . Jest oczywiste, że taka funkcja jest jedyną, która spełnia $g = f \circ k$ .

Dla studentów, którzy zetknęli się z toposami, warto w tym miejscu dodać, że monomorfizmy są ekwalizatorami w dowolnym toposie.

==Zadanie 3.11==

Pokazać, że w dowolnej kategorii epi ekwalizator jest izomorfizmem.

Rozwiązanie:

Rozważmy diagram:

Skoro $e$ jest ekwalizatorem $f, g$ , mamy $f \circ e = g \circ e$ . Epimorficzność daje $f = g$ , czyli $f \circ 1_{A} = g \circ 1_{A}$ . Dla identyczności $1_{A}$ spełniony jest warunek (1) definicji ekwalizatora, a zatem istnieje dokładnie jedna strzałka $k : A \to E$ taka, że $e \circ k = 1_{A}$ . Pokażemy, że $k \circ e = 1_{E}$ , co zakończy dowód. Ale przecież $e \circ k = 1_{A}$ implikuje $e \circ k \circ e = 1_{A} \circ e = e = e \circ 1_{E}$ . Każdy ekwalizator jest mono, więc upraszcza się z lewej strony, co daje: $k \circ e = 1_{E}$ .

==Zadanie 3.12==

Wykazać, że w posecie $(P, \leq)$ ekwalizatorami są identyczności.

Rozwiązanie:

Element $e \in P$ będzie ekwalizatorem $p \leq q$ , jeśli z faktu $s \leq p \leq q$ wynika $s \leq e$ , dla każdego $s \in P$ . To jest możliwe tylko, gdy $e = p$ , czyli gdy ekwalizator jest identycznością $e \leq e$ .

==Zadanie 3.13==

Wykazać, że jeśli $f : A \to B$ jest funkcją i $C \subseteq B$ , to przeciwobraz $f^{- 1}$ jest pulbakiem $f$ i inkluzji $i : C \to B$ .

Rozwiązanie:

W $𝐒 𝐞 𝐭$ wiemy dokładnie, jak wygląda pulbak $f : A \to B$ i zanurzenia $i : C \to B$ :

A \times_{B} C = {(a, c) \in A \times C ∣ f (a) = i (c)}

czyli:

A \times_{B} C = {(a, f (a)) \in A \times C ∣ f (a) \in C}

który to zbiór jest izomorficzny z $f^{- 1} [C]$ .

==Zadanie 3.14==

W $𝐒 𝐞 𝐭$ , czym jest pulbak dla diagramu: $A \overset{f}{\to} B \overset{f}{\leftarrow} A$ ?

Rozwiązanie:

Jest to zbiór ${(a, b) \in A \times A ∣ f (a) = f (b)}$ , czyli relacja równoważności, którą wyznacza $f$ na $A \times A$ .

==Zadanie 3.15==

Udowodnij, że w pulbak monomorfizmu jest monomorfizmem.

Wskazówka:

Musimy pokazać, że w diagramie:

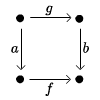
jeśli $f$ jest mono, to $g$ też.

Rozwiązanie:

Załóżmy, że $f$ mono i na diagramie:

niech $g k = g h$ . Skoro $b g h = b g k = f a k$ , to istnieje dokładnie jedna strzałka $z$ taka, że $a z = a k$ i $g h = g z$ . Oczywiście, podstawiając $k$ za $z$ , widzimy, że $z = k$ , z jedyności. Podstawiając $h$ za $z$ , wystarczy sprawdzić, że $a h = a k$ , ale to prawda, bo $f a h = b g h = b g k = f a k$ i $f$ jest mono, co daje upragnioną równość: $a h = a k$ . Pokazaliśmy, że $k = z = h$ , czyli $g$ jest mono.

==Zadanie 3.16==

Zdefiniuj pushout, posługując się Zasadą Dualności.

Rozwiązanie:

Biorąc definicję pulbaku i stosując ściśle zasadę dualności, dostajemy tekst:

Pushoutem strzałek $f, g$ takich, że $d o m (f) = d o m (g)$ w kategorii $𝐂$

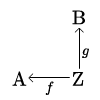
nazywamy obiekt $Q$ wraz ze strzałkami

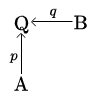
taki, że:

poniższy kwadrat pushoutowy komutuje, tzn. $p \circ f = q \circ g$ oraz
uniwersalny, tzn. dla dowolnego innego kandydata na pushout

A \overset{r}{⟵} R \overset{s}{⟶} B

istnieje dokładnie jedna strzałka $u : Q \to R$ taka, że: $r = u \circ p$ i $s = u \circ q$ , tzn. taka, że poniższy diagram komutuje:

To jest właśnie szukana definicja.

Teoria kategorii dla informatyków/Ćwiczenia 3: Zasada dualności i proste konstrukcje uniwersalne

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia