Teoria kategorii dla informatyków/Ćwiczenia 10: Sprzężenia II

==Zadanie 10.1==

Udowodnić, że $F⊣G$, $F^{\prime }⊣G^{\prime }$ oraz $G\cong G^{\prime }$ implikują $F\cong F^{\prime }$.

Wskazówka:

Użyć wniosku z lematu Yonedy.

Rozwiązanie:

Z założeń wynika istnienie następującego ciągu naturalnych izomorfizmów, dla dowolnych $A,B$:

$\mathrm{H}\mathrm{o}\mathrm{m}(FA,B)\cong \mathrm{H}\mathrm{o}\mathrm{m}(A,GB)\cong \mathrm{H}\mathrm{o}\mathrm{m}(A,G^{\prime }B)\cong \mathrm{H}\mathrm{o}\mathrm{m}(F^{\prime }A,B)$ (po kolei wykorzystaliśmy: sprzężenie $F⊣G$, zachowywanie izomorfizmu przez funktor Yonedy, sprzężenie $F^{\prime }⊣G^{\prime }$). Z wniosku z lematu Yonedy, udowodnionego w Zadaniu 7.2, wynika, że $F\cong F^{\prime }$.

==Zadanie 10.2==

Udowodnić, że jeśli $F⊣G$ oraz $H⊣K$, to $H\circ F⊣G\circ K$.

Rozwiązanie:

Następujący ciąg naturalnych izomorfizmów, prawdziwy dla dowolnych $A,B$, dowodzi tezy zadania:

$\mathrm{H}\mathrm{o}\mathrm{m}(HFA,B)\cong \mathrm{H}\mathrm{o}\mathrm{m}(FA,KB)\cong \mathrm{H}\mathrm{o}\mathrm{m}(A,GKB)$

==Zadanie 10.3==

Udowodnij Twierdzenie 10.3 bez użycia lematu Yonedy.

Rozwiązanie:

Załóżmy, że $G:\mathbf{𝐃}\to \mathbf{𝐂}$ ma lewe sprzężenie $F$. Niech $D:\mathbf{𝐉}\to \mathbf{𝐃}$ będzie diagramem, który ma granicę:

$\{c_j:Y\to D(j)\mid j\in {\mathbf{𝐉}}_0\}$

Musimy pokazać, że:

$\{G{c}_j:GY\to GD(j)\mid j\in {\mathbf{𝐉}}_0\}$

jest granicą diagramu $G\circ D:\mathbf{𝐉}\to \mathbf{𝐂}$. Dla dowolnego stożka

$\{d_j:X\to GD(j)\mid j\in {\mathbf{𝐉}}_0\}$

nad $G\circ D$, używając sprzężenia, dostajemy stożek:

$\{\widehat{d_j}:FX\to D(j)\mid j\in {\mathbf{𝐉}}_0\}$

Z definicji granicy, diagram:

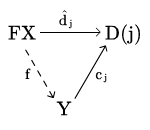
komutuje, czyli, używając sprzężenia,

komutuje. To kończy dowód.

==Zadanie 10.4==

Udowodnij, że funkcja monotoniczna pomiędzy dwoma kratami zupełnymi posiada lewe sprzężenie wtedy i tylko wtedy, gdy zachowuje wszystkie infima. Jakie jest twierdzenie dualne?

Wskazówka:

Oczywiście, twierdzenie dualne brzmi: funkcja monotoniczna $f:L\to K$ ma prawe sprzężenie wtedy i tylko wtedy, gdy zachowuje wszelkie suprema, tzn. $f(\underset{i}{\bigvee }{x}_i)=\underset{i}{\bigvee }f(x_i)$ dla dowolnej rodziny elementów $\{x_i\}\subseteq L$.

Zauważmy też, że w świetle Twierdzenia 10.3, aby rozwiązać oryginalne zadanie, wystarczy połowa pracy.

Rozwiązanie:

Niech $f:L\to K$ będzie monotoniczna i niech zachowuje wszystkie infima. Zdefiniujmy funkcję $g:K\to L$ jako:

$g(y):=\bigwedge \{z\in L\mid y\le f(z)\}$

Wtedy $g$ jest monotoniczna: załóżmy, że $x\le y$. Wtedy dla każdego $z\in L$, jeśli $y\le f(z)$, to $x\le f(z)$, co świadczy już o tym, że $g(x)\le g(y)$. Pokażmy teraz, że $g$ ma lewe sprzężenie. Z definicji $g$ wprost wynika, że jeśli $f(a)\le b$, to $g(f(a))=\bigwedge \{z\mid f(z)\le f(a)\}=f(a)\le g(B)$. Z drugiej strony, jeśli $a\le g(b)$, to $f(a)\le f(g(b))=\underset{b\le f(z)}{\bigwedge }f(z)=b$. To kończy dowód.

==Zadanie 10.5==

Udowodnić, że kategoria lokalnie mała i zupełna $\mathbf{𝐂}$ posiada obiekt początkowy wtedy i tylko wtedy, gdy spełniony jest następujący warunek itnienia zbioru rozwiązań: istnieje zbiór obiektów $C_i$ taki, że dla dowolnego obiektu $C\in {\mathbf{𝐂}}_0$ istnieje strzałka $C_i\to C$ dla pewnego $i\in I$.

Wskazówka:

Jeśli $\mathbf{𝐂}$ ma obiekt początkowy $\mathbf{𝟎}$, to singleton $\{\mathbf{𝟎}\}$ jest zbiorem rozwiązań. Odwrotnie, jeśli istnieje zbiór rozwiązań $\{C_i\mid i\in I\}$, rozważamy produkt $W:={\mathrm{\Pi }}_i{C}_i$. Tenże produkt jest słabo początkowy, w tym sensie, że dla dowolnego obiektu $C\in {\mathbf{𝐂}}_0$ istnieje (niekoniecznie jedyna!) strzałka typu $W\to C$, a mianowicie złożenie:

${\mathrm{\Pi }}_i{C}_i\stackrel{p_i}{\to }{C}_i\to C$

(dla każdego $i\in I$ mamy bowiem projekcję $p_i:{\mathrm{\Pi }}_i{C}_i\to C_i$). Ponieważ ${\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(W,W)$ jest zbiorem, bo $\mathbf{𝐂}$ jest lokalnie mała, możemy rozważać granicę diagramu

wszystkich strzałek typu $W\to W$. Ta granica, niech nazywa się $(E,e)$,

istnieje, bo $\mathbf{𝐂}$ jest kategorią zupełną. Teraz wystarczy udowodnić, że $E$ jest obiektem początkowym w $\mathbf{𝐂}$.

Rozwiązanie:

Granica $(E,e)$, jak zdefiniowana powyżej, posiada następujące własności:

• dla dowolnych endostrzałek $f,g\in {\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(W,W)$ mamy $fe=ge$;
• jeśli $h:A\to W$ jest strzałką taką, że dla każdej pary strzałek $f,g\in {\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(W,W)$ takich, że $fh=gh$, istnieje dokładnie jedna strzałka $k:A\to E$ z $ek=h$.

Innymi słowy, $E$ jest pewnym uogólnionym ekwalizatorem. Pokażemy, że $E$ jest początkowy w $\mathbf{𝐂}$. Niech $A\in {\mathbf{𝐂}}_0$ będzie dowolnym obiektem. Skoro $W$ jest obiektem słabo początkowym, istnieje strzałka

$E\stackrel{e}{\to }W\stackrel{p_i}{\to }{C}_i\to A$

Czy jest to jedyna strzałka tego typu? Tak, bo jeśli mamy dwie równoległe strzałki $f,g:E\to A$, to niech $(B,h)$ będzie ich ekwalizatorem. Ponieważ $W$ jest słabo początkowy, znów znajdziemy strzałkę $k:W\to B$. Wtedy $ehk$ jest typu $W\to W$. Skoro $E$ jest ekwalizatorem, to $1_{P}e=(ehk)e$, a zatem $e{1}_E=e(hke)$. Drugi warunek na $E$ implikuje, że $e$ jest mono, więc $1_E=hke$. I w końcu $f=f{1}_E=fhke=ghke=g{1}_E=g$. To kończy dowód.

==Zadanie 10.6==

Udowodnić Fakt 10.7.

Rozwiązanie:

Załóżmy $d⊣g$. Skoro $t\le g(s)$ wtedy i tylko wtedy, gdy $d(t)\le s$, to oczywiście $d(t)$ jest ograniczeniem dolnym $g^{-1}(\uparrow t)$. Ale $d(t)\le d(t)$ implikuje $t\le g(d(t))$, więc $d(t)\in g^{-1}(\uparrow t)$, co świadczy o tym, że $d(t)=\mathrm{m}\mathrm{i}\mathrm{n}\{g^{-1}(\uparrow t)\}$ dla każdego $t\in T$. Odwrotnie, załóżmy, że $d$ jest scharakteryzowana przez $g$ jak wyżej. Niech $t\le g(s)$. Wtedy $s\in g^{-1}(\uparrow t)$, co daje $s\ge \mathrm{m}\mathrm{i}\mathrm{n}{g}^{-1}(\uparrow t)=d(t)$. Z drugiej strony, niech $m=\mathrm{m}\mathrm{i}\mathrm{n}{g}^{-1}(\uparrow t)$, czyli $m\in g^{-1}(\uparrow t)$, a więc $g(m)\ge t$. Jeśli zatem zachodzi $s\ge d(t)=m$, to $g(s)\ge g(m)\ge t$, gdyż $g$ jest monotoniczna. To kończy dowód.

==Zadanie 10.7==

Udowodnij Fakt 10.9.

Rozwiązanie:

Niech $d⊣g$. Wówczas z $g(s)\le g(s)$ wynika $dg(s)\le s$. Dualnie $t\ge gd(t)$. Odwrotnie, załóżmy te nierówności. Niech $t\le g(s)$. Wtedy $d(t)\le dg(s)$, bo $d$ monotoniczna. Z założenia $dg(s)\le s$, więc $d(t)\le s$. Podobnie, jeśli $s\ge d(t)$, to $g(s)\ge gd(t)\ge t$.

Zauważmy teraz, że $dg\le 1$ implikuje $gdg\le g$ z monotoniczności. Ale dla $t=g(s)$ z założenia $1\le gd$, mamy że $g(s)\le gdg(s)$, czyli $g\le gdg$. Pokazaliśmy, że $g=gdg$. Podobnie dowodzi się $d=dgd$. Idempotentność: $g=gdg$ implikuje $dg=dgdg$, zaś $d=dgd$ implikuje $gd=gdgd$, co należało pokazać.

==Zadanie==

Udowodnij Fakt Fakt 10.10.

Rozwiązanie:

Udowodnimy równoważność pierwszych czterech warunków:

1. $g$ jest surjekcją;
2. $d(t)=\mathrm{m}\mathrm{i}\mathrm{n}{g}^{-1}(t)$ dla każdego $t\in T$;
3. $gd=1_T$;
4. $d$ jest injekcją.

w przypadku, gdy $d⊣g$.

Załóżmy (1). Z Zadania 10.6 wynika, że $d(t)=\mathrm{m}\mathrm{i}\mathrm{n}{g}^{-1}(\uparrow t)$. Skoro $g$ jest surjekcją, $g(g^{-1}(\uparrow t))=\uparrow t$. Z monotoniczności, $g(d(t))=\mathrm{m}\mathrm{i}\mathrm{n}g(g^{-1}(\uparrow t))=\mathrm{m}\mathrm{i}\mathrm{n}\uparrow t=t$. A zatem $d(t)\in g^{-1}(t)$, czyli $\mathrm{m}\mathrm{i}\mathrm{n}{g}^{-1}(t)=d(t)$, co jest (2). Załóżmy (2). Mamy $d(t)\in g^{-1}(t)$, tzn. $g(d(t))=t$, czyli (3). Załóżmy (3). Wtedy $d$ jest sekcją, a zatem jest injekcją. Załóżmy (4). Skoro $d=dgd$ i $d$ jest injekcją, to jest monomorfizmem, więc $1_T=gd$, a zatem $g$ jest retrakcją, czyli surjekcją. To pokazuje (1) i kończy dowód.