Teoria kategorii dla informatyków/Ćwiczenia 14: Teoria dziedzin III

==Zadanie 14.1==

Udowodnić, że w $\mathbf{𝐃}\mathbf{𝐜}\mathbf{𝐩}\mathbf{𝐨}$ są granice dowolnych diagramów.

Wskazówka:

Dowód przeprowadzimy dla szczególnego diagramu:

$D_0\stackrel{f_0}{\leftarrow }{D}_1\stackrel{f_1}{\leftarrow }{D}_2\stackrel{f_2}{\leftarrow }{D}_3\stackrel{f_3}{\leftarrow }{D}_4\stackrel{f_4}{\leftarrow }..$

(Dowód ogólny jest analogiczny lecz wymaga bardziej technicznego zapisu, więc go pominiemy.) Pokażemy, że granica powyższego diagramu jest dana jako:

$D=\{(x_0,x_1,...)\mid (\mathrm{\forall }n\in \omega )(f_n(x_{n+1})=x_n)\}$

Rozwiązanie:

Zauważmy, że zbiór $D$ jest posetem, w którym elementy są uporządkowane po współrzędnych (to znaczy, że porządek jest dziedziczony z produktu ${\mathrm{\Pi }}_{n\in \omega }{D}_n$).

Jeśli $GD$, to dla każdego $n\in \omega$ zbiór ${\pi }_n[G]=\{x_n\mid x\in G\}$ jest skierowanym podzbiorem $D_n$. Niech $y_n=\bigvee {}^{\downarrow }\{x_n\mid x\in G\}$. Z ciągłości funkcji tworzących diagram mamy:

$f_n(y_{n+1})=\bigvee {}^{\downarrow }{f}_n(\{x_{n+1}\mid x\in G\})=\bigvee {}^{\downarrow }\{x_n\mid x\in G\}=y_n$

To znaczy, że $(y_0,y_1,...)\in D$ i, jak łatwo zauważyć, element ten jest supremum skierowanym zbioru $G$. Pokazaliśmy więc, że $D\in \mathbf{𝐃}\mathbf{𝐜}\mathbf{𝐩}\mathbf{𝐨}$.

Udowodnimy teraz, że $D$ wraz z projekcjami $\{{\pi }_n:D\to D_n\mid n\in \omega \}$ jest granicą. Po pierwsze, dla $GD$ mamy:

${\pi }_n(\bigvee {}^{\downarrow }G)=y_n=\bigvee {}^{\downarrow }\{x_n\mid x\in G\}=\bigvee {}^{\downarrow }{\pi }_n[G]$

a więc projekcje są ciągłe.

Po drugie, jeśli $\{g_k:E\to D_k\mid k\in \omega \}$ jest dowolną inną granicą, to zdefiniujmy $h:E\to D$ jako:

$h(x)=(g_0(x),g_1(x),...)$ Z definicji powyższej wynika, że dla każdego $k\in \omega$ mamy ${\pi }_k\circ h=g_k$. Zauważmy, że to świadczy o jednoznaczności wyboru $h$. A zatem $D$ jest granicą omawianego diagramu. Co więcej, z jednoznaczności granicy, wnioskujemy, że $D\cong E$.

==Zadanie 14.2==

Udowodnić Lemat 14.5.

Rozwiązanie:

Skoro $D_{\mathrm{\infty }}$ jest granicą odwrotną diagramu

to

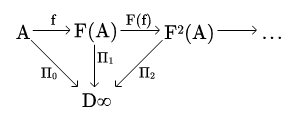
komutuje. W szczególności

komutuje i jak łatwo zauważyć $D_{\mathrm{\infty }}$ jest jego granicą. Ale z ciągłości $F$ mamy, że diagram

komutuje i $F(D_{\mathrm{\infty }})$ jest jego granicą. A zatem $D_{\mathrm{\infty }}\cong F(D_{\mathrm{\infty }})$ wynika z jednoznaczności granicy.

Poniższe zadania zawierają przykłady rozwiązań rekursywnych równań w kategorii ${\mathbf{𝐃}\mathbf{𝐜}\mathbf{𝐩}\mathbf{𝐨}}_{\mathrm{\perp }}$. Wszystkie te rozwiązania konstruujemy w następujący sposób: mając dany lokalnie ciągły funktor $F$, definiujemy rekursywnie ciąg kolejnych dcpo, poczynając od posetu jednoelementowego $\mathbf{𝟏}$ (czyli elementu końcowego w ${\mathbf{𝐃}\mathbf{𝐜}\mathbf{𝐩}\mathbf{𝐨}}_{\mathrm{\perp }}$):

$D_0:=\mathbf{𝟏},D_1:=F\mathbf{𝟏},...,D_{n+1}:=F^n\mathbf{𝟏},..$

wraz z odpowiednimi, naturalnymi parami e-p. Taki ciąg tworzy diagram. Funktor $F$, zgodnie z Lematem 14.7, rozszerza się do funktora ciągłego, a zatem Lemat 14.5 mówi, że dla granicy $D_{\mathrm{\infty }}$ diagramu mamy $F(D_{\mathrm{\infty }})\cong D_{\mathrm{\infty }}$. W poniższych zadaniach zamiast podawania szczegółowych dowodów kładziemy nacisk na intuicyjne zrozumienie konstrukcji $D_{\mathrm{\infty }}$ dla prostych funktorów.

==Zadanie 14.3==

Znaleźć punkt stały funktora $F:{\mathbf{𝐃}\mathbf{𝐜}\mathbf{𝐩}\mathbf{𝐨}}_{\mathrm{\perp }}\to {\mathbf{𝐃}\mathbf{𝐜}\mathbf{𝐩}\mathbf{𝐨}}_{\mathrm{\perp }}$, który dodaje element najmniejszy: $F(-):=(-{)}_{\mathrm{\perp }}$.

Wskazówka:

Porządna definicja mogłaby wyglądać tak: dla obiektu $D$, $F(D):=D_{\mathrm{\perp }}$. Dla morfizmu $f:P\to Q$,

$F(f):=f_{\mathrm{\perp }}:P_{\mathrm{\perp }}\to Q_{\mathrm{\perp }},f(p\in P):=p,f(\mathrm{\perp }):=\mathrm{\perp }$

Rozwiązanie:

Najpierw pokażmy, że $F$ jest lokalnie ciągły. W tym celu musimy pokazać, że operacja $f:P\to Q\mapsto f_{\mathrm{\perp }}:P_{\mathrm{\perp }}\to Q_{\mathrm{\perp }}$ typu

$\mathrm{H}\mathrm{o}\mathrm{m}(P,Q)\to \mathrm{H}\mathrm{o}\mathrm{m}(P_{\mathrm{\perp }},Q_{\mathrm{\perp }})$

jest ciągła w sensie Scotta. Niech $\{f_i\}$ będzie skierowanym podzbiorem $\mathrm{H}\mathrm{o}\mathrm{m}(P,Q)$. Ponieważ $\mathrm{H}\mathrm{o}\mathrm{m}(P,Q)$ jest dcpo, ta rodzina ma supremum $\bigvee {}_i^{\downarrow }{f}_i$. Wówczas: $F(\bigvee {}_i^{\downarrow }{f}_i)(x\in P_{\mathrm{\perp }})=\{\begin{array}{ll}\bigvee {}_i^{\downarrow }{f}_i(x),& x\ne \mathrm{\perp }\\ \mathrm{\perp },& x=\mathrm{\perp }.\end{array}$ Z drugiej strony: $\bigvee {}_i^{\downarrow }F(f_i)(x)=\bigvee {}_i^{\downarrow }{f}_{i\mathrm{\perp }}(x)=\{\begin{array}{ll}\bigvee {}_i^{\downarrow }{f}_i(x),& x\ne \mathrm{\perp }\\ \mathrm{\perp },& x=\mathrm{\perp }.\end{array}$ A to oznacza, że $F$ jest ciągły w sensie Scotta, czyli lokalnie ciągły.

Znajdźmy więc punkt stały tego funktora, tj. rozwiążmy rekursywne równanie:

$X\cong X_{\mathrm{\perp }}$

Zaczynając od posetu jednoelementowego $\mathbf{𝟏}$, mamy ${\mathbf{𝟏}}_{\mathrm{\perp }}=2$, itd. jak na rysunku (strzałkami zaznaczono projekcje, zanurzenia są oczywiste, nieprawdaż?):

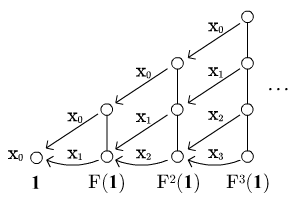
Oczywiście, granicą tego diagramu są liczby naturalne z elementem największym:

Łatwo to zobaczyć, prawda?

==Zadanie 14.4==

Znajdź rozwiązanie równania:

$X={\mathbf{𝟏}}_{\mathrm{\perp }}+X$

gdzie $+$ jest koproduktem w kategorii ${\mathbf{𝐃}\mathbf{𝐜}\mathbf{𝐩}\mathbf{𝐨}}_{\mathrm{\perp }}$.

Wskazówka:

Koprodukt w ${\mathbf{𝐃}\mathbf{𝐜}\mathbf{𝐩}\mathbf{𝐨}}_{\mathrm{\perp }}$ nie może być oczywiście tylko sumą rozłączną, tak jak w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$, ponieważ suma dwóch obiektów nie byłaby posetem z elementem najmniejszym. Ale łatwo pokazać, że koproduktem jest suma rozłączna, w którym dwa elementy najmniejsze identyfikujemy ze sobą:

Formalnie, na obiektach koprodukt jest zdefiniowany jako:

$P+Q:=\{(p,0)\mid p\in P\}\cup \{(q,1)\mid q\in Q\}$

wraz z zanurzeniami:

$i_P(x):=\{\begin{array}{ll}(x,0)& x\in P\\ \mathrm{\perp }& x=\mathrm{\perp },\end{array}$

$i_Q(x):=\{\begin{array}{ll}(x,1)& x\in Q\\ \mathrm{\perp }& x=\mathrm{\perp }.\end{array}$

Rozwiązanie:

Aby wykazać lokalną ciągłość koproduktu, trzeba pokazać, że odwzorowanie:

$(f:P\to R,g:Q\to S)\mapsto f+g:P+Q\to R+S$

jest ciągłe w sensie Scotta. To odwzorowanie ma typ:

$\mathrm{H}\mathrm{o}\mathrm{m}(P,R)\times \mathrm{H}\mathrm{o}\mathrm{m}(Q,S)\mapsto \mathrm{H}\mathrm{o}\mathrm{m}(P+Q,R+S)$

a zatem zgodnie z Lematem 13.2, wystarczy wykazać ciągłość ze względu na każdy argument z osobna. To sprowadza się do pokazania dwóch (analogicznych) równości, z których jedną z nich:

$f+\bigvee {}_i^{\downarrow }{g}_i=\bigvee {}_i^{\downarrow }(f+g_i)$

dla dowolnego zbioru skierowanego $\{g_i\}$ funkcji ciągłych, wykażemy. Jest jasne, że:

$f+g=\{\begin{array}{ll}(i_R\circ f)(x),& x\in P\\ (i_S\circ g)(x),& x\in Q\\ \mathrm{\perp },& x=\mathrm{\perp }.\end{array}$

A zatem:

$f+\bigvee {}_i^{\downarrow }{g}_i=\{\begin{array}{ll}(i_R\circ f)(x),& x\in P\\ (i_S\circ \bigvee {}_i^{\downarrow }{g}_i)(x),& x\in Q\\ \mathrm{\perp },& x=\mathrm{\perp }\end{array}=\{\begin{array}{ll}(i_R\circ f)(x),& x\in P\\ \bigvee {}_i^{\downarrow }(i_S\circ g_i)(x),& x\in Q\\ \mathrm{\perp },& x=\mathrm{\perp }\end{array}=\bigvee {}_i^{\downarrow }(f+g_i)$

Można powiedzieć, że $+$ jest lokalnie ciągły, bo wszystkie funkcje użyte w jego definicji są ciągłe w sensie Scotta.

Rozwiązaniem równania $X\cong {\mathbf{𝟏}}_{\mathrm{\perp }}+X$, jak widzimy na rysunku:

<flash>file=tk-14.21K.swf|width=400|height=200</flash>

są płaskie liczby naturalne ${\mathbb{\mathbb{N}}}_{\mathrm{\perp }}$.

==Zadanie 14.5==

Znaleźć rozwiązanie równania:

$X\cong \mathbf{𝟏}\oplus X$

gdzie $F(P,Q):=P\oplus Q$ jest sumą rozłączna $P$ i $Q$, do której dodany jest nowy element najmniejszy.

Wskazówka:

Oto przykład działania funktora sumy rozłącznej na obiektach:

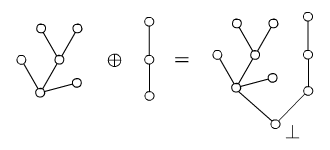
Rozwiązanie:

Rozwiązaniem są leniwe liczby naturalne:

<flash>file=tk-14.19.swf|width=350|height=350</flash>

==Zadanie 14.6==

Rozwiązać równanie:

$X\cong X\oplus X$

Rozwiązanie:

Rozwiązaniem jest nieskończone drzewo binarne (dziedzina ${\mathrm{\Sigma }}^{\mathrm{\infty }}$ znana z Przykładu 12.12). Na animacji zaznaczono część projekcji.

<flash>file=tk-14.18.swf|width=500|height=300</flash>

==Zadanie 14.7==

Rozwiązać równanie:

$X\cong {\mathbf{𝟏}}_{\mathrm{\perp }}+({\mathbb{\mathbb{N}}}_{\mathrm{\perp }}\otimes X)$

gdzie: ${\mathbb{\mathbb{N}}}_{\mathrm{\perp }}$ to znane z Zadania 14.4 płaskie liczby naturalne, zaś $F(P,Q):=P\otimes Q$ jest funktorem przypisującym dcpo $P$,$Q$ ich produkt zredukowany (ang. smash product) $P\otimes Q$. Produkt zredukowany jest ilorazem produktu $P\times Q$ przez relację równoważności $\equiv$, która identyfikuje ze sobą wszystkie elementy produktu, w których na choćby jednej współrzędnej znajduje się $\mathrm{\perp }$.

Rozwiązanie:

Nie tak trudno zobaczyć, że $P\otimes Q$ jest koekwalizatorem dwóch projekcji ${\pi }_P:\equiv \to P\times Q$ i ${\pi }_Q:\equiv \to P\times Q$. Ten koekwalizator $[\cdot ]:P\times Q\to P\otimes Q$ jest więc ciągły w sensie Scotta, a co za tym idzie, dla $f:P\to R$ i $g:Q\to S$, funkcja:

$f\otimes g:=[(f\circ {\pi }_P,g\circ {\pi }_Q)]$

jak na rysunku:

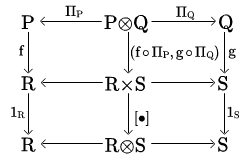
jest ciągła w sensie Scotta. Dlatego też $F$ jest funktorem lokalnie ciągłym.

Rozwiązaniem równania:

$X\cong {\mathbf{𝟏}}_{\mathrm{\perp }}+({\mathbb{\mathbb{N}}}_{\mathrm{\perp }}\otimes X)$ jest dziedzina skończonych i nieskończonych list liczb naturalnych. Elementy tej dziedziny różne od $\mathrm{\perp }$ są albo listą pustą, albo listą skończoną, albo listą nieskończoną. Powyższe równanie należy intuicyjnie czytać jako: lista jest albo pusta, albo jest parą składającą się z liczby naturalnej i listy, albo jest niezdefiniowana. Czy Czytelnik to widzi?