Teoria kategorii dla informatyków/Ćwiczenia 12: Teoria dziedzin I

==Zadanie 12.1==

Niech $(P,\le )$ będzie częściowym porządkiem i niech $A,B\subseteq P$. Pokaż, że jeśli $\downarrow A=\downarrow B$ to $\bigvee A$ istnieje wtedy i tylko wtedy, gdy $\bigvee B$ istnieje i w obu przypadkach te suprema są sobie równe.

Wskazówka:

Wystarczy pokazać, że dowolne ograniczenie górne zbioru $A$ jest ograniczeniem górnym zbioru $B$.

Rozwiązanie:

Niech $A\le u$ dla pewnego $u\in P$. Wówczas dla $x\in \downarrow A$ mamy $x\le a$ dla $a\in A<ath>icozatymidzie<math>x\le u$. Pokazaliśmy, że $\downarrow A\le u$. A zatem $B\subseteq \downarrow B=\downarrow A\le u$. Udowodniliśmy więc, że dowolne ograniczenie górne $u$ zbioru $A$ jest ograniczeniem górnym zbioru $B$. A zatem najmniejsze ograniczenie górne (jeśli istnieje) zbioru $A$ jest najmniejszym ograniczeniem górnym zbioru $B$, co kończy dowód.

==Zadanie 12.2==

Niech ${𝒟}$ będzie skierowaną przez inkluzję rodziną skierowanych podzbiorów posetu $(P,\le )$. Udowodnij, że $\bigcup {𝒟}$ jest skierowanym podzbiorem $P$.

Wskazówka:

Nie zapomnijmy o wykazaniu niepustości $\bigcup {𝒟}$.

Rozwiązanie:

Jeśli $D\in {𝒟}$, to istnieje $x\in D$, bo $D$ niepusty. A zatem $x\in \bigcup {𝒟}$, co świadczy o niepustości tego zbioru.

Niech teraz $a,b\in \bigcup {𝒟}$. Wówczas istnieją $D_a,D_b\in {𝒟}$ takie, że odpowiednio $a\in D_a$ oraz $b\in D_b$. Skoro rodzina ${𝒟}$ jest skierowana przez inkluzję, to istnieje $D\in {𝒟}$ taki, że $D_a,D_b\subseteq D$, co daje nam $a,b\in D$. Ponieważ $D$ jest skierowanym podzbiorem $P$, istnieje $z\in D\subseteq \bigcup {𝒟}$ taki, że $a,b\le z$. A to świadczy o tym, że zbiór $\bigcup {𝒟}$ jest skierowany.

==Zadanie 12.3==

Niech $(A_i{)}_{i\in I}$ będzie dowolną indeksowaną rodziną podzbiorów częściowego porządku $(P,\le )$ posiadających suprema w $P$. Pokaż, że zbiory $\{\bigvee A_i\mid i\in I\}$ oraz $\bigcup _{i\in I}{A}_i$ mają te same ograniczenia górne (a co za tym suprema, o ile chociaż jedno z nich istnieje).

Wskazówka:

Zauważmy, że dowolne ograniczenie górne pierwszego ze zbiorów jest ograniczeniem górnym dla każdego ze zbiorów $A_i$.

Rozwiązanie:

Niech $\{\bigvee A_i\mid i\in I\}\le u$ dla pewnego $u\in P$. Wówczas dla każdego $i\in I$ mamy $A_i\le u$, co daje $\bigcup A_i\le u$. Rozumowanie powyższe daje się odwrócić, więc tak naprawdę pokazaliśmy, że $\{\bigvee A_i\mid i\in I\}\le u$ wtedy i tylko wtedy, gdy $\bigcup A_i\le u$, co kończy dowód.

==Zadanie 12.4==

Niech $(P,\le )$ będzie częściowym porządkiem, $A,B\subseteq P$ oraz $\downarrow A=\downarrow B$. Udowodnij, że $A$ jest skierowany wtedy i tylko wtedy, gdy $B$ jest skierowany. Wyciągnij wniosek, że dowolny podzbiór $X$ posetu $P$ jest skierowany wtedy i tylko wtedy, gdy jego domknięcie dolne $\downarrow X$ jest skierowany.

Rozwiązanie:

Przypuśćmy, że $A$ jest skierowany. Wówczas istnieje $a\in A$. Oczywiście $a\in A\subseteq \downarrow A=\downarrow B$, co oznacza, że $a\in \downarrow B$. A zatem istnieje $b\in B$ taki, że $a\le b$. W szczególności, $B$ jest zbiorem niepustym.

Podobnie wnioskując, zauważamy, że jeśli $b_1,a_2\in A$, to istnieją $a_1,a_2\in A$ takie, że $b_1\le a_1$ oraz $b_2\le a_2$. Ponieważ $A$ jest skierowany, istnieje $a\in A$ taki, że $a_1,a_2\le a$. W szczególności $b_1,b_2\le a$ i $a\in \downarrow A=\downarrow B$. To znaczy, że istnieje $b\in B$ taki, że $a\le b$, a co za tym idzie $b_1,b_2\le b$. Zbiór $B$ jest więc skierowany. Z symetrii założeń wynika pierwsza z tez zadania.

Druga z tez wynika natychmiast z obserwacji $\downarrow X=\downarrow \downarrow X$.

==Zadanie 12.5==

Niech $(P,\le )$ będzie częściowym porządkiem. Pokaż, że jeśli $D$ jest podzbiorem skierowanym $P$, który posiada supremum, zaś $A$ pewnym podzbiorem $P$ oraz $\downarrow A=\downarrow D$, to $A$ jest skierowany i jego supremum jest równe supremum $D$.

Wskazówka:

Wykorzystaj Zadania 12.2 i 12.3.

Rozwiązanie:

Skoro $\downarrow A=\downarrow D$ i $\downarrow D$ jest skierowany, to z Zadania 12.3 wynika, że $A$ jest skierowany, a z Zadania 12.2 wynika, że supremum $A$ istnieje i jest równe $\bigvee D$.

==Zadanie 12.6==

Niech $(P,\le )$ będzie częściowym porządkiem. Udowodnij, że dwa poniższe warunki są równoważne: (i) każdy podzbiór $P$ ograniczony z góry posiada supremum; (ii) każdy niepusty podzbiór $P$ posiada infimum.

Rozwiązanie:

Załóżmy (i). Niech $\mathrm{\varnothing }\ne A\subseteq P$. Niech $B$ będzie zbiorem ograniczeń dolnych $A$. Oczywiście $B$ jest ograniczony z góry przez dowolny element zbioru $A$. Z założenia, $B$ osiada supremum, które jest największym ograniczeniem dolnym $A$, czyli jego infimum.

Podobnie, dla dowolnego zbioru $C$ ograniczonego z góry, jego supremum jest dane jako infimum zbioru ograniczeń górnych $C$.

W końcu zauważmy, że poset $P$, w którym jeden z równoważnych warunków (i) lub (ii) jest spełniony, posiada element najmniejszy $\mathrm{\perp }$, który - zgodnie z tym, co udowodniliśmy powyżej - powstaje jako supremum zbioru pustego (równoważnie: jako infimum $P$).

==Zadanie 12.7==

Wskaż taki częściowy porządek $P$, że:

1. jest dcpo, ale nie jest bc-zupełny,
2. jest ciągły, ale nie jest algebraiczny,
3. jest nieciągły i jest dcpo,
4. nie jest dcpo, ale jest ciągły,
5. jego relacja aproksymacji jest pusta.

Wskazówka:

Warto rozważać niewielkie przykłady.

Rozwiązanie:

1. Niech $P=\{\mathrm{\perp },x,y,z,w\}$ oraz niech $\le$ będzie przechodnim domknięciem relacji $\{(\mathrm{\perp },x),(\mathrm{\perp },y),(x,z),(y,z),(x,w),(y,w)\}$. Tutaj oczywiście podzbiór $\{x,y\}$ posiada ograniczenia górne, ale nie posiada supremum.

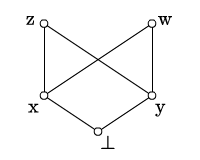
2. Niech $P=\omega \cup \{\mathrm{\top },x\}$. Porządek definiujemy tak, że $\mathrm{\top }$ jest elementem największym, liczby z $\omega$ są uporządkowane w sposób naturalny, zaś $x$ jest powyżej $0$, poniżej $\mathrm{\top }$ i nieporównywalny z żadną inną liczbą naturalną. W takim posecie nie zachodzi $x=\bigvee \ll x$, co już łatwo pokazać.

3. Poprzedni przykład wystarcza.

4. Liczby naturalne $\omega$.

5. Wystarczy wziąć dwie kopie liczb naturalnych i dołączyć element największy.

==Zadanie 12.8==

Pokazać, że w przestrzeni topologicznej $(X,\tau )$, która jest $T_0$ zachodzi $\mathbf{𝐜}\mathbf{𝐥}\{x\}={\downarrow }_{\tau }x$, gdzie ${\le }_{\tau }$ jest porządkiem specjalizacji.

Wskazówka:

Topologia Scotta na dowolnym częściowym porządku jest tutaj dobrym przykładem.

Rozwiązanie:

Wystarczy zauważyć, że $y\notin \mathbf{𝐜}\mathbf{𝐥}\{x\}$ wtedy i tylko wtedy, gdy istnieje zbiór domknięty $C$ zawierający $x$ i taki, że $y\notin C$. Ale to jest równoważne stwierdzeniu, że istnieje zbiór otwarty $U:=X\setminus C$ taki, że $y\in U$ i $x\notin U$ lub po prostu $y\notin {\downarrow }_{\tau }x$, co należało pokazać.

==Zadanie 12.9==

Niech $\sigma$ oznacza topologię Scotta na posecie ciągłym $(P,\le )$. Pokaż, że Parser nie mógł rozpoznać (nieznana funkcja „\uparrowarrow”): {\displaystyle \mathbf{int}_{\sigma}(\uparrowarrow x) = \Uparrow x} dla dowolnego $x\in P$.

Wskazówka:

Istotnym założeniem jest ciągłość posetu, która gwarantuje nam, że relacja aproksymacji jest interpolatywna (por. Twierdzenie 12.3).

Rozwiązanie:

Po pierwsze pokażmy, że $\Uparrow x$ jest zbiorem otwartym w sensie Scotta. Z własności (w2) relacji aproksymacji łatwo wynika, że $\Uparrow x$ jest zbiorem górnym. Jeśli teraz $\bigvee D=z\in \Uparrow x$ dla pewnego zbioru skierowanego Parser nie mógł rozpoznać (nieznana funkcja „\uparrowarrow”): {\displaystyle D\subseteq {}^{\uparrowarrow} P} , to z własności interpolacji (Twierdzenie 12.3) znajdujemy $x\ll w\ll z$ i dalej z definicji relacji aproksymacji dostajemy $d\in D$ taki, że $w\le d$. Mamy więc albo $x\ll w\le d$, czyli z (w2) $x\ll d$, albo $d\in \Uparrow x$, co dowodzi, że $\Uparrow x$ jest otwarty w sensie Scotta.

Jeśli teraz Parser nie mógł rozpoznać (nieznana funkcja „\uparrowarrow”): {\displaystyle \sigma\ni U\subseteq \uparrowarrow x} , to weźmy dowolny element $u\in U$. Ponieważ $P$ jest ciągły, Parser nie mógł rozpoznać (nieznana funkcja „\uparrowarrow”): {\displaystyle u = \bigvee {}^{\uparrowarrow}\ll u} . A zatem z otwartości $U$ wynika, że istnieje $z\in \ll u$ taki, że $z\in U$. Pokazaliśmy więc, że $x\le z\ll u$, czyli $u\in \Uparrow x$. Z dowolności wyboru $u$ dostajemy $U\subseteq \Uparrow x$; innymi słowy, $\Uparrow x$ jest największym zbiorem otwartym zawartym w Parser nie mógł rozpoznać (nieznana funkcja „\uparrowarrow”): {\displaystyle \uparrowarrow x} , czyli wnętrzem zbioru Parser nie mógł rozpoznać (nieznana funkcja „\uparrowarrow”): {\displaystyle \uparrowarrow x} , co należało pokazać.

==Zadanie 12.10==

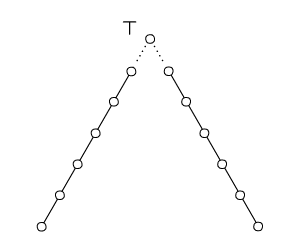
Pokazać, że topologia Scotta na dowolnym posecie ciągłym ma bazę złożoną z filtrów.

Wskazówka:

Należy pamiętać (Zadanie 12.7), że w posecie ciągłym zbiory typu $\Uparrow x$ są otwarte w topologii Scotta, ale w ogólności nie są filtrami, co pokazuje poniższy rysunek:

Rozwiązanie:

Niech $P$ będzie posetem ciągłym. Weźmy zbiór otwarty $U\subseteq P$ oraz element $x\in U$. Trzeba teraz pokazać, że istnieje filtr $F\in \sigma (P)$ taki, że $x\in F\subseteq U$. Zbiór $F$ konstruujemy, jak następuje: połóżmy $x_0=x$. Ponieważ $U$ jest otwarty, to istnieje $x_1\ll x_0$ taki, że $x_1\in U$. Podobnie dla dowolnego $x_n\in U$ znajdziemy $x_{n+1}\in U$ tak, że $x_{n+1}\ll x_n$. Wystarczy teraz położyć $F=\bigcup _{n\in \omega }\Uparrow x_n$. Jest oczywiste, że $F$ jest zarówno zbiorem otwartym, jak i to, że jest filtrem!