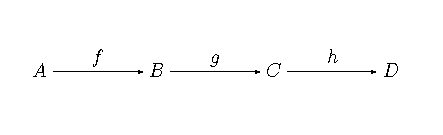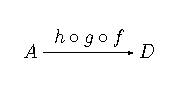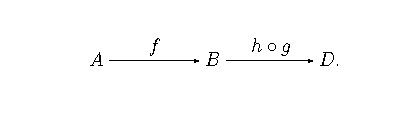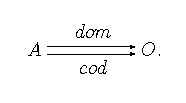TKI Moduł 1

Teoria kategorii jako ogólny dział algebry wyrosła z prac Samuela Eilenberga i Saundersa MacLane'a: pionierską pracą jest tu General theory of natural equivalences, Transactions of the American Mathematical Society 58 (1945), pp. 231-294 - autorzy wprowadzili tam pojęcie kategorii, funktora i naturalnej transformacji funktorów. Teoria kategorii szybko przekroczyła granice algebry i jej język okazał się uniwersalnym sposobem mówienia o innych teoriach matematycznych: logice, teorii zbiorów, topologii, teorii porządku, geometrii, analizie itd. Jak to możliwe? Treść tych wykładów stanowi jedną z odpowiedzi na to pytanie.

Definicja kategorii

Zacznijmy od definicji z teorii mnogości: jak pamiętamy, funkcja $f:A\to B$ jest bijekcją jeśli jest różnowartościową surjekcją, tj.

$\mathrm{\forall }x,y\in Af(x)=f(y)⟹x=y$ oraz

$\mathrm{\forall }z\in B\mathrm{\exists }x\in Af(x)=z$.

Zauważmy, że drugi warunek pozwala nam każdemu elementowi $z$ zbioru $B$ przyporządkować element $x$ zbioru $A$, zaś warunek pierwszy mówi, że to przekształcenie (nazwijmy je $g$) jest funkcją (śmiało napiszmy więc $g:B\to A$). W tym świetle z warunku drugiego wynika, że złożenie $f\circ g$ jest funkcją identycznościową na zbiorze $B$, a stąd wynika $f\circ g\circ f=f$, co w połączeniu z pierwszym warunkiem oznacza, że $g\circ f$ jest identycznością na zbiorze $A$. Idąc dalej tym tropem (patrz Zadanie 1.1.) jesteśmy w stanie bez trudu pokazać, że:

Fakt 1.1. Funkcja $f:A\to B$ jest bijekcją wtedy i tylko wtedy, 
gdy  istnieje funkcja $g:B\to A$ taka, że 
$f\circ g=1_B$ oraz $g\circ f=1_A$.

Sam wynik nie wygląda, być może, ekscytująco, ale w koniunkcji z kolejnymi przykładami pozwoli nam wyciągnąć ekscytujące wnioski.

Rozważmy zatem zbiór liczb naturalnych $N$. Teoria mnogości definiuje $N$ jako najmniejszy zbiór zawierający liczbę zero $0$ (definiowaną jako zbiór pusty) i spełniający: $n\in N⟹succ(n)\in N$, gdzie $succ:N\to N$ jest funkcją następnika (definiowaną jako $succ(n)=n\cup \{n\}$). Okazuje się, że zbiór liczb naturalnych można wyróżnić spośród innych zbiorów w ten sposób (Zadanie 1.2):

Fakt 1.2. Zbiór liczb naturalnych $N$ jest to zbiór 
zawierający liczbę zero oraz wyposażony w funkcję $s:N\to N$ taką, że:
dla dowolnego zbioru $X$ i elementu $e\in X$ 
oraz funkcji $g:X\to X$ 
istnieje dokładnie jedna funkcja $f:N\to X$
spełniająca dwa warunki: $f(0)=e$ oraz $f\circ s=g\circ f$.

Dwa powyższe przykłady wskazują na to, że definicje teorii mnogości można wyrażać operując jedynie pojęciem funkcji i złożenia funkcji (zauważmy, że elementy zbiorów można traktować jako funkcje, których dziedziną jest singleton). Postawmy więc śmiałe pytanie: czy można prezentować różnorodne teorie matematyczne badając jedynie własności przekształceń obiektów matematycznych będących przedmiotem zainteresowania danej teorii? A zatem pytamy czy: można prezentować teorię mnogości badając własności funkcji między zbiorami, teorię grup badając własności homomorfizmów grup, topologię badając własności funkcji ciągłych pomiędzy przestrzeniami topologicznymi? W ogólności zapytajmy więc jeszcze raz: czy można badać dowolne obiekty matematyczne z określoną strukturą za pomocą własności przekształceń, które tę strukturę zachowują?

Odpowiedź brzmi: tak; i ta właśnie twierdząca odpowiedź powołuje do życia teorię kategorii. Teoria kategorii składa się bowiem z twierdzeń dotyczących uniwersalnych własności przekształceń, niezależnych od cech szczególnych danych teorii matematycznych. Tak więc, teoria kategorii bada wspólne, uniwersalne własnościami zbiorów, grup, przestrzeni topologicznych, przestrzeni wektorowych, częściowych porządków, i tak dalej, wszystko w języku przekształceń danej struktury.

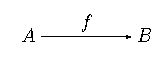
Rozpocznijmy pewien eksperyment. Dokonajmy szybko pierwszej, nieformalnej próby stworzenia aksjomatycznej teorii przekształceń. Przekształcenie nazywać będziemy również morfizmem lub po prostu strzałką. Przekształcenie działa pomiędzy obiektami, np. funkcja to przekształcenie zbiorów, homomorfizm to przekształcenie grupy w grupę, funkcja ciągła to przekształcenie przestrzeni topolgicznej w przestrzeń topologiczną, funkcja monotoniczna to przekształcenie posetu w poset, itd. (Załóżmy na początku dla prostoty, że w naszych przykładach nie bierzemy pod uwagę przekształceń obiektów pewnej klasy w inną klasę, na przykład wyznacznika, który przekształca macierz w liczbę. Takimi morfizmami zajmiemy się poźniej.) Każde przekształcenie $f$ działa na pewien jedyny obiekt, nazwijmy go dziedziną $f$ i oznaczmy $\mathrm{d}\mathrm{o}\mathrm{m}(f)$, i przekształca go w inny jedyny obiekt nazywany przeciwdziedziną $f$ i oznaczany jako $\mathrm{c}\mathrm{o}\mathrm{d}(f)$. Fakt, że morfizm $f$ ma dziedzinę $A$ i przeciwdziedzinę $B$ zapisujemy

lub po prostu $f:A\to B$. Nasza teoria nie może istnieć bez pojęcia złożenia przekształceń: zakładamy, że dwóm morfizmom $f,g$ takim, że $\mathrm{c}\mathrm{o}\mathrm{d}(g)=\mathrm{d}\mathrm{o}\mathrm{m}(f)$ (strzałki takie nazywamy składalnymi) przypisujemy morfizm $f\circ g$ zwany złożeniem, dla którego mamy $\mathrm{d}\mathrm{o}\mathrm{m}(f\circ g)=\mathrm{d}\mathrm{o}\mathrm{m}(g)$ i $\mathrm{c}\mathrm{o}\mathrm{d}(f\circ g)=\mathrm{c}\mathrm{o}\mathrm{d}(f)$. Przykłady wskazują na to, że kolejność złożenia składalnych przekształceń nie powinna grać roli, czyli dla:

morfizm:

może powstać albo z:

albo, równoważnie, z:

W końcu, w naszej nieformalnej teorii przekształceń postulujemy istnienie przekształceń, które - nieformalnie mówiąc: nic nie zmieniają, tak zwanych identyczności:

To kończy nieformalny opis języka, w którym główną rolę grają przekształcenia. Zapiszmy to teraz formalnie.

Definicja 1.3. Kategoria $\mathbf{𝐂}$ składa się z:

1. obiektów: $A,B,C,..$.,
2. morfizmów $f,g,h,..$.,
3. dwóch operacji $\mathrm{d}\mathrm{o}\mathrm{m},\mathrm{c}\mathrm{o}\mathrm{d}$ przypisującej każdemu morfizmowi $f$ obiekty $\mathrm{d}\mathrm{o}\mathrm{m}(f)$i $\mathrm{c}\mathrm{o}\mathrm{d}(f)$,
4. operacji $1$ przypisującej każdemu obiektowi $A$ morfizm $1_A$ nazywany identycznością,
5. operacji $\circ$ przypisującej każdej parze morfizmów $f,g$ takich, że $\mathrm{c}\mathrm{o}\mathrm{d}(g)=\mathrm{d}\mathrm{o}\mathrm{m}(f)$ morfizm $f\circ g$ nazywany złożeniem

spełniających następujące aksjomaty:

K1.$\mathrm{d}\mathrm{o}\mathrm{m}(1_A)=A=\mathrm{c}\mathrm{o}\mathrm{d}(1_A)$; $\mathrm{d}\mathrm{o}\mathrm{m}(f\circ g)=\mathrm{d}\mathrm{o}\mathrm{m}(g)$; $\mathrm{c}\mathrm{o}\mathrm{d}(f\circ g)=\mathrm{c}\mathrm{o}\mathrm{d}(f)$,

K2.$f\circ 1_A=f=1_B\circ f$, gdzie $A=\mathrm{d}\mathrm{o}\mathrm{m}(f)$ oraz $B=\mathrm{c}\mathrm{o}\mathrm{d}(f)$,

K3.jeśli $f,g$ są składalne oraz $g,h$ są składalne, to $(f\circ g)\circ h=f\circ (g\circ h)$.

(Dla dociekliwych: aby wypowiedzieć powyższą definicję jeszcze ściślej, należałoby powiedzieć, że kategorią nazywamy dowolną interpretację powyższych aksjomatów na gruncie teorii mnogości.)

Pokażmy, że o kategorii można też myśleć jako o specjalnym grafie skierowanym.

Definicja 1.4. Grafem skierowanym nazywamy kolekcję obiektów (wierzchołków) $O$, kolekcję strzałek (krawędzi) $A$ i dwie funkcje

W grafie, kolekcja składalnych par strzałek to zbiór

$A{\times }_{O}A=\{(g,f)\mid g,f\in A\wedge \mathrm{d}\mathrm{o}\mathrm{m}(g)=\mathrm{c}\mathrm{o}\mathrm{d}(f)\}$

nazywany produktem nad $O$. O kategorii można myśleć jako o grafie skierowanym $\mathbf{𝐂}$, który posiada dwie dodatkowe funkcje $1:O\to A$, $C\mapsto 1_C$ oraz $\circ :A{\times }_{O}A\to A$, $(g,f)\mapsto g\circ f$ takie, że spełnione są warunki K1-K3 Definicji 1.3.

Poniżej pokażemy trzecią, równoważną, algebraiczną definicję kategorii (na podstawie: Peter J. Freyd, Andre Scedrov Categories, Allegories}, North Holland, 1989.

Definicja 1.5. Kategoria $\mathbf{𝐂}$ składa się z dwóch operacji unarnych i jednej częściowej operacji binarnej. Zmienne, na które działają te operacje nazywamy morfizmami (strzałkami). Wartości tych operacji są zapisywane i czytane jako:

Operacje podlegają następującym aksjomatom:

(b1) $xy$ jest zdefiniowane wtw, gdy $x◻=◻y$,

(b2) $(◻x)◻=◻x$ oraz $◻(x◻)=x◻$,

(b3) $(◻x)x=x$ oraz $x(x◻)=x$,

(b4) $◻(xy)=◻(x(◻y))$ oraz $(xy)◻=((x◻)y)◻$

(b5) $x(yz)=(xy)z$.

W tym wypadku równoważność definicji z dwiema pozostałymi (Definicje 1.3. i 1.4) nie jest oczywista. Aby ją wykazać, rozpocznijmy od lematu, który rzuci troche światła na strukturę algebraiczną, którą przed chwilą opisaliśmy.

Lemat 1.6 Dla morfizmu $e$ następujące warunki są równoważne:

1. istnieje $x$ taki, że $e=◻x$;
2. istnieje $y$ taki, że $e=y◻$;
3. $e=◻e$;
4. $e=e◻$;
5. dla każdego $x$, $ex\approx x$ (co oznacza, że jeśli złożenie $ex$ jest zdefiniowane, to jest równe $x$),
6. dla każdego $x$, $xe\approx x$.

Dowód: (1)$\to$(2) Dla $y=◻x$ mamy $y◻=(◻x)◻=◻x=e$. (2)$\to$(3) $◻e=◻(y◻)=y◻=e$. (3)$\to$(4) $e◻=(◻e)◻)=◻e=e$. (4)$\to$(5) Załóżmy, że $ex$ jest zdefiniowane dla każdego $x$; to oznacza, że $e◻=◻x$, czyli z (4), $e=◻x$ dla każdego $x$. A zatem $ex=(◻x)x=x$. (3)$\to$(1) Oczywiste. (4)$\to$(3) $◻e=◻(e◻)=e◻=e$. (5)$\to$(4) Połóżmy $x=e◻$. Mamy $◻x=◻(e◻)=e◻$, czyli $ex$ istnieje. Z (5) wynika, że $e(e◻)=e◻$. Ale (b3) implikuje, że $e(e◻)=e$, czyli $e=e◻$. Dowód równoważności (6) z (3) jest podobny do równoważności (5) z (4).

Morfizm $e$ spełniający dowolny z powyższych warunków nazywamy identycznością.

A zatem równoważność trzeciej definicji kategorii z pierwszą uzyskujemy następująco (tak naprawdę, to pokażemy jedynie, że dane Definicji 1.5. wystarczą do zrekonstruowania Definicji 1.3.: Identyczność $1_x$ to zmienna $x$ taka, że $x=◻x=x◻$. Dziedziną $x$ jest $◻x$, przeciwdziedziną $x◻$. Złożenie $x\circ y$ to $yx$. Kolekcja obiektów Definicji 1.3. pokrywa się z kolekcją morfizmów identycznościowych Definicji 1.5.. Zauważmy, że dla dowolnego $x$, zarówno $◻x$, jak i $x◻$ są obiektami (identycznościami), bo $◻(◻x)=◻x$, $(◻x)◻=◻x$, $(x◻)◻=(◻(x◻))◻=◻(x◻)=x◻$, $◻(x◻)=x◻$.

Sprawdźmy aksjomaty: $\mathrm{d}\mathrm{o}\mathrm{m}(1_x)=◻x=x=x◻=\mathrm{c}\mathrm{o}\mathrm{d}(1_x)$. Aby pokazać, że $f$ jest morfizmem, załóżmy, że $x=\mathrm{d}\mathrm{o}\mathrm{m}(f)$(czyli $1_x=◻f$) oraz $y=\mathrm{c}\mathrm{o}\mathrm{d}(f)$ (czyli $1_y=f◻$)). Wówczas $f\circ 1_x=1_{x}f=(◻f)f=f$, $1_y\circ f=f{1}_y=f(f◻)=f$.

Załóżmy teraz, że $\mathrm{d}\mathrm{o}\mathrm{m}(f)=\mathrm{c}\mathrm{o}\mathrm{d}(g)$. Wówczas $\mathrm{d}\mathrm{o}\mathrm{m}(f\circ g)=◻(gf)=◻(g◻f)=\mathrm{d}\mathrm{o}\mathrm{m}(1_{\mathrm{d}\mathrm{o}\mathrm{m}(f)}\circ g)=\mathrm{d}\mathrm{o}\mathrm{m}(1_{\mathrm{c}\mathrm{o}\mathrm{d}(g)}\circ g)=\mathrm{d}\mathrm{o}\mathrm{m}(g)$. Ostatnia równość wynika z poprzedniego paragrafu. Podobnie, $\mathrm{c}\mathrm{o}\mathrm{d}(f\circ g)=(gf)◻=((g◻)f)◻=\mathrm{c}\mathrm{o}\mathrm{d}(f\circ 1_{\mathrm{c}\mathrm{o}\mathrm{d}(g)})=\mathrm{c}\mathrm{o}\mathrm{d}(f\circ 1_{\mathrm{d}\mathrm{o}\mathrm{m}(f)})=\mathrm{c}\mathrm{o}\mathrm{d}(f)$.

W końcu, $f\circ (g\circ h)=(hg)f=h(gf)=(f\circ g)\circ h$ przy odpowiednich założeniach.

Przykłady kategorii

• $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$. Obiektami są zbiory, morfizmami funkcje. Uwaga: W teorii mnogości funkcja jest zdefiniowana jako zbiór par uporządkowanych takich, że

$((x,y)\in f\wedge (x,y^{\prime })\in f)⟹y=y^{\prime }$.

Aby traktować funkcje jako morfizmy musimy precyzyjnie znać $\mathrm{d}\mathrm{o}\mathrm{m}(f)$ i $\mathrm{c}\mathrm{o}\mathrm{d}(f)$. Na przykład funkcje $\sin :\mathbb{ℝ}\to [-1,1]$ oraz $\sin :\mathbb{ℝ}\to \mathbb{ℝ}$, które mają takie samo działanie na argumentach, będą traktowane jako dwa różne morfizmy. Formalnie, w języku teorii mnogości morfizmem będzie trójka $(X,f,Y)$ taka, że $f\subseteq X\times Y$ spełnia powyższe równanie w ramce oraz poniższe:

$x\in X⟹(\mathrm{\exists }y\in Y(x,y)\in f)$.

Wtedy $\mathrm{d}\mathrm{o}\mathrm{m}$ jest projekcją na pierwszą współrzędną $(X,f,Y)\mapsto X$, a $\mathrm{c}\mathrm{o}\mathrm{d}$ projekcją na trzecią współrzędną.

• Kategoria zbiorów skończonych i funkcji ${\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}}_{fin}$, jak również wiele innych kategorii, w których obiektami i

morfizmami są ograniczone klasy zbiorów i funkcji, np. kategoria wszystkich zbiorów skończonych i injekcji.

• Kategorie, w których obiektami są zbiory z pewną dodatkową stukturą algebraiczną, zaś morfizmami te funkcje, które tę strukturę zachowują.
  • $\mathbf{𝐕}\mathbf{𝐞}\mathbf{𝐜}\mathbf{𝐭}$ Przestrzenie wektorowe i odwzorowania liniowe
  • $\mathbf{𝐆}\mathbf{𝐫}\mathbf{𝐩}$ Grupy i homomorfizmy grup
  • $\mathbf{𝐀}\mathbf{𝐛}$ Grupy abelowe i homomorfizmy grup
  • $\mathbf{𝐌}\mathbf{𝐨}\mathbf{𝐧}$ Monoidy i homomorfizmy monoidów
  • $\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}$ Częściowe porządki i funkcje monotoniczne
  • $\mathbf{𝐓}\mathbf{𝐨}\mathbf{𝐩}$ Przestrzenie topologiczne i funkcje ciągłe
  • $\mathbf{𝐆}\mathbf{𝐫}\mathbf{𝐚}\mathbf{𝐩}\mathbf{𝐡}$ Grafy i homomorfizmy grafów
  • liczby naturalne i wszystkie funkcje obliczalne

• Mając dowolny częściowy porządek (poset) $(P,\le )$ definiujemy kategorię o tej samej nazwie $P$ jak następuje: jako obiekty bierzemy elementy $P$, zaś dla dwóch obiektów $x,y\in P$ przyjmujemy, że istnieje morfizm z $x$ do $y$ wtedy i tylko wtedy, gdy $x\le y$.

• $\mathbf{𝐑}\mathbf{𝐞}\mathbf{𝐥}$ Obiektami tej kategorii są zbiory, zaś morfizmami relacje binarne, tzn. $f:A\to B$ wtedy i tylko wtedy, gdy $f\subseteq A\times B$. Wówczas rolę identyczności spełniają relacje identycznościowe: $1_A=\{(a,a)\mid a\in A\}$, zaś złożeniem morfizmów jest po prostu złożenie relacji znane z kursu teorii mnogości: mając dane $R\subseteq A\times B$ oraz $S\subseteq B\times C$ przyjmujemy:

$(a,c)\in S\circ R\iff \mathrm{\exists }b\in B((a,b)\in R\wedge (b,c)\in S)$

• Kategorie skończone (skończoność dotyczy ilości istniejących morfizmów, choć nazwy tych kategorii odnoszą się do ilości obiektów):
  • $\mathbf{𝟏}$ Ta kategoria ma jeden obiekt i jedą strzałkę: identyczność.
  • $\mathbf{𝟎}$ Ta kategoria nie ma obiektów i nie ma strzałek.
  • $\mathbf{𝟐}$ Kategoria ta ma dwa obiekty i jedną strzałkę pomiędzy nimi (a także oczywiście dwie wymagane identyczności).
  • $\mathbf{𝟑}$ Kategoria ma trzy obiekty, trzy identyczności, dokładnie jedną strzałkę z obiektu pierwszego do drugiego, dokładnie jedną strzałkę z obiektu drugiego do trzeciego i dokładnie jedną strzałkę z obiektu pierwszego do trzeciego (co oznacza, że ta ostatnia musi być złożeniem dwóch pozostałych nieidentycznościowych strzałek!)
  • Inne kategorie skończone możemy tworzyć biorąc skończoną ilość obiektów wraz z odpowiadającymi im identycznościami, a następnie dodając dowolną skończoną ilość morfizmów. W tym wypadku musimy jednak zadbać o to, aby - jeśli morfizmy będą tworzyły cykle - zadeklarować złożenie wszystkich morfizmów w cyklu jako równe odpowiedniej identyczności. W innym bowiem przypadku uzyskana kategoria nie będzie już skończona (będzie miała nieskończenie wiele morfizmów).

• Kategorie dyskretne są to takie kategorie, w których nie ma innych morfizmów niż identyczności. Łatwo pokazać, że kategorie dyskretne możemy utożsamiać ze zbiorami.

• Niech $(M,*,e)$ będzie monoidem z jedynką $e$. Wówczas biorąc $M$ jako jedyny obiekt, zaś elementy $M$ jako morfizmy (z dziedziną i kodziedziną $M$, zaś działanie $*$ jako złożenie morfizmów, otrzymujemy kategorię. Można łatwo pokazać również konstrukcję odwrotną, tj. przekonać się, że każda kategoria z jednym obiektem może być traktowana jako monoid. Mówiąc krótko: kategorie z jednym obiektem to monoidy. (Jak w takim razie traktować grupy? Odpowiedź znajdziemy jeszcze przed końcem wykładu...)

Inne przykłady kategorii zamieścimy w Ćwiczeniach do tego wykładu.

Izomorfizmy

Definicja izomorfizmu jest pierwszą definicją teorii kategorii, definicją abstrakcyjną, niezależną od specyficznych wymagań konkretnej teorii matematycznej, definicją wyrażoną tylko w języku strzałek.

Definicja 1.7. Niech $\mathbf{𝐂}$ będzie dowolną kategorią. Morfizm $f:A\to B$ jest izomorfizmem jeśli istnieje morfizm $g:B\to A$ taki, że $f\circ g=1_B$ oraz $g\circ f=1_A$. Morfizm $g$ nazywa się morfizmem odwrotnym do $f$. Jeśli dla obiektów $A,B$ kategorii $\mathbf{𝐂}$ istnieje izomorfizm $f:A\to B$, to obiekty $A$ i $B$ nazywamy izomorficznymi, co zapisujemy jako $A\cong B$.

Ponieważ dowolny morfizm $f$ posiada dokładnie jeden morfizm odwrotny (dowód?), będziemy go oznaczać jako $f^{-1}$. Można łatwo pokazać (dowód?), że morfizm odwrotny do izomorfizmu jest izomorfizmem.

Fakt 1.1. wyraża zatem myśl, że izomorfizmami w $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ są dokładnie bijekcje. Ale uwaga: w kategoriach, których obiektami są zbiory z pewną strukturą, a morfizmami funkcje zachowujące tę strukturę, bijekcje nie zawsze są izomorfizmami. Prosty kontrprzykład stanowi tutaj kategoria $\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}$ (Zadanie xxx).

Podstawy teoriomnogościowe

Teoria mnogości uczy nas, że nie istnieje zbiór wszystkich zbiorów. Jeśli więc rozważamy kategorię $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$, której obiektami są zbiory, to widzimy, że kolekcja wszystkich obiektów $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ nie tworzy zbioru (jest zbyt duża!). Podobnie, kolekcja wszystkich morfizmów $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ jest zbyt wielka, aby być zbiorem (zauważmy, że samych identyczności jest już tyle, ile obiektów). Kategoria $\mathbf{𝐒}\mathbf{𝐞}\mathbf{𝐭}$ nie jest taką jedyną. W związku z tym definiujemy:

Definicja 1.8 Kategorię $\mathbf{𝐂}$ nazywamy małą, jeśli kolekcja wszystkich obiektów ${\mathbf{𝐂}}_0$ i morfizmów ${\mathbf{𝐂}}_1$ kategorii $\mathbf{𝐂}$ są zbiorami. W przeciwnym wypadku $\mathbf{𝐂}$ jest duża.

A zatem $\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}$, $\mathbf{𝐆}\mathbf{𝐫}\mathbf{𝐩}$, $\mathbf{𝐕}\mathbf{𝐞}\mathbf{𝐜}$ są duże, zaś kategorie skończone są małe. Kategorie duże wyglądają na pierwszy rzut oka bardzo nieprzyjaźnie, część z nich posiada jednak bardzo często następującą cechę:

Definicja 1.9. Kategorię $\mathbf{𝐂}$ nazywamy lokalnie małą, jeśli dla każdej pary obiektów $A,B$ z $\mathbf{𝐂}$ kolekcja ${\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathbf{𝐂}}(A,B)=\{f\in {\mathbf{𝐂}}_1\mid f:A\to B\}$ jest zbiorem (o takim zbiorze mówimy w skrócie homset, podobnie jak o zbiorze częściowo uporządkowanym przyjęło się mówić: poset).

Większa część teorii kategorii, którą zaprezentujemy w dalszym toku wykładu dotyczy kategorii lokalnie małych (takich jak $\mathbf{𝐏}\mathbf{𝐨}\mathbf{𝐬}$, $\mathbf{𝐆}\mathbf{𝐫}\mathbf{𝐩}$, $\mathbf{𝐕}\mathbf{𝐞}\mathbf{𝐜}$ itd. czy wszystkie kategorie małe). Po dalsze wiadomości dotyczące podstaw teoriomnogościowych teorii kategorii odsyłamy do dyskusji tego tematu w Categories for the Working Mathematician Saundersa MacLane'a.