TC Moduł 4
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania

|
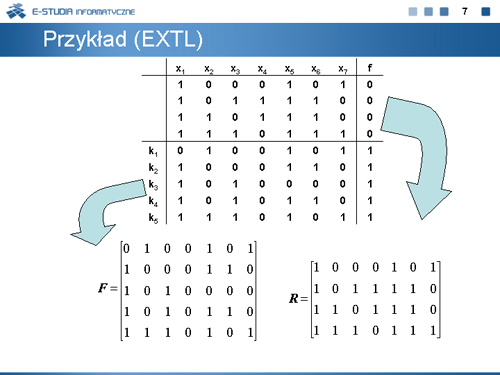
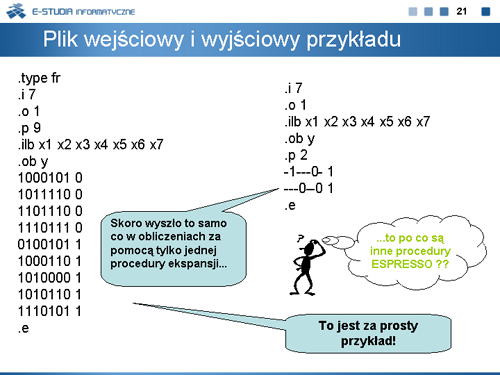
Minimalizacja funkcji boolowskich metodą ekspansji. |

|
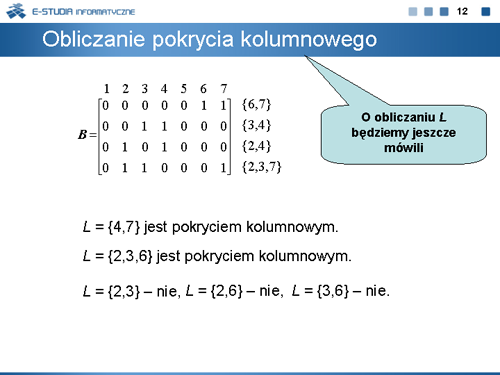
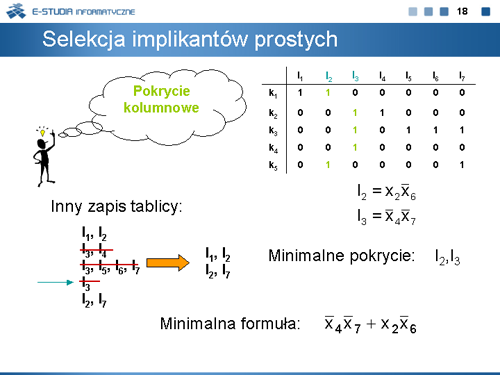
Pokryciem kolumnowym macierzy , , jest zbiór taki, że dla każdego istnieje , dla którego . Pokrycie kolumnowe nazywamy minimalnym, jeżeli nie istnieje , który jest pokryciem macierzy . |