Sw3.6-m1-1.2-Slajd14
Systemy wbudowane(10)
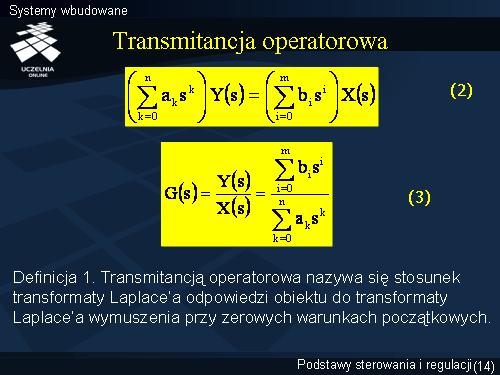
Stosując do równania różniczkowego (1) obustronne przekształcenie Laplace'a i wykorzystując twierdzenie o transformacie pochodnej otrzymujemy równanie, które po przekształceniu przyjmuje postać (2),
gdzie: Y(s ) – transformata Laplace'a wielkości wyjściowej y(t ),
X(s ) – transformata Laplace'a wielkości wejściowej x(t ).
Z równania (2) wyznaczymy stosunek Y(s ) do X(s ).
D e f i n i c j a 1. Transmitancją operatorową nazywa się stosunek transformaty Laplace'a odpowiedzi do transformaty Laplace'a wymuszenia przy zerowych warunkach początkowych.
Pojecie transmitancji operatorowej jest jednym z najważniejszych pojęć w teorii sterowania. Transmitancja operatorowa jest pewną formą opisu dynamiki obiektów, najczęściej wykorzystywaną w analizie i syntezie układów sterowania. Transmitancja pozwala uzyskać niezbędne dane o obiekcie i jego zachowaniu się w przypadku różnych wymuszeń. W celu określenia tego zachowania wyznacza się dla danego obiektu jego charakterystyki czasowe.