SW wykład 8 - Slajd9
Częściowe porządki zupełne Przykłady Funkcje ciągłe Intuicje Intuicje, c.d. Przestrzeń funkcji częściowych Twierdzenie o punkcie stałym Techniki dowodowe Semantyka while
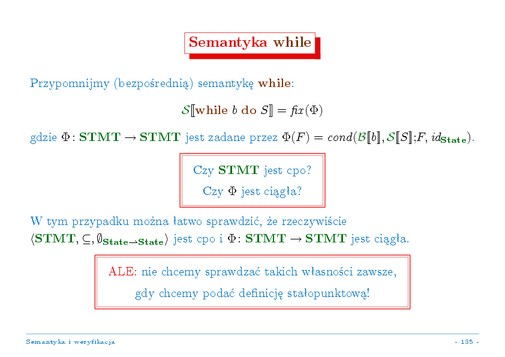
Wróćmy jeszcze na chwilę do definicji znaczenia instrukcji pętli omawianej na wykładzie 4 (pierwszy wykład o semantyce denotacyjnej). Przypomnijmy, że znaczenie to definiowaliśmy tam jako najmniejszy punkt stały pewnego operatora na dziedzinie znaczeń instrukcji. W świetle właśnie wprowadzonej teorii, trzebaby pokazać, że dziedzina znaczeń instrukcji jest zbiorem łańcuchowo zupełnym, a rozważany operator jest funkcją ciągła na tym zbiorze. W tym przypadku, pierwsza własność jest oczywista: dziedziną znaczeń instrukcji był zbiór funkcji częściowych (ze stanów w stany), który ze standardowym porządkiem jest naszym najbardziej typowym przykładem zbioru łańcuchowo zupełnego. Łatwo też można pokazać, że rozważany operator jest funkcją ciągłą na tym zbiorze.
Ale: przecież potem mieliśmy jeszcze kilkakroć do czynienia ze stałopunktowymi definicjami znaczeń pewnych fraz różnych rozszerzeń języka TINY. Czy dowody łańcuchowej zupełności odpowiednich dziedzin i ciągłości odpowiednich operatorów będą podobnie łatwe? A nawet jeśli tak, to czy naprawdę musimy je przeprowadzać dla każdego przypadku kolejno? W kolejnym wykładzie pokażemy, jak można takiej konieczności uniknąć ograniczając się do bogatego, ale ustalonego z góry zasobu metod konstruowania dziedzin semantycznych i budowania funkcji określających znaczenia fraz języka.