SW wykład 12 - Slajd18
Zadanie programistyczne Przykład Problemy z logiką Hoare'a Poprawność całkowita Poprawność całkowita, c.d. Poprawność całkowita, c.d. Reguła dla pętli Poprawność systemu dowodzenia dla Tiny Pełność systemu dowodzenia dla Tiny Przykład Uogólnienie Poprawność i pełność Relacje dobrze ufundowane Dowodzenie poprawności całkowitej Przykład Przykład Kolejny problem Binarne warunki końcowe Warunki poprawności Reguły dowodzenia Reguły dowodzenia, c.d. Przykład Logika algorytmiczna System dowodzenia
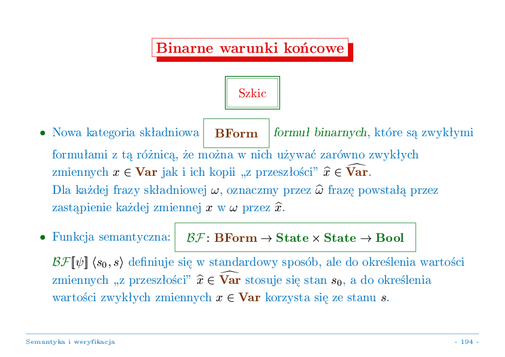
Naszkicujmy najpierw podejście do pojęcia poprawności bliskie bardzo omawianemu powyżej, ale oparte o całkowitą poprawność programów względem zwykłego warunku wstępnego i binarnego warunku końcowego. Warunki binarne mają za zadanie opisywać relacje na stanach (a nie zbiory stanów, jak zwykłe warunki). Formalnie, możemy je wprowadzić jako formuły pierwszego rzędu budowane nad dwoma kopiami zbioru zmiennych: są to zwykłe zmienne, opisujące wartości tych zmiennych w stanie "bieżącym" (gdy warunek binarny jest wykorzystywany jako warunek końcowy, chodzi tu o końcowy stan programu), oraz ich wersje ozdobione specjalnym znacznikiem --- "znacznikiem stanu początkowego" --- opisujące wartości zmiennych (w wersji bez dekoracji) w stanie początkowym. Semantyka takich formuł w naturalny zatem sposób przyporządkowuje każdej parze stanów wartość logiczną, albo równoważnie, określa relację między stanami (w której są te i tylko te pary stanów, dla których znaczeniem formuły jest prawda). Zauważmy, że każda "zwykła" formuła jest też warunkiem binarnym, który zachodzi dla każdej pary stanów takiej, że jej drugi element (stan bieżący) spełnia tę formułę w zwykłym sensie.
Aha: dla każdej frazy składni języka, budować będziemy jej wersję "w stanie początkowym" przez oznakowanie wszystkich występujących w niej zmiennych tym "znacznikiem stanu początkowego".