SW wykład 10 - Slajd9
Poprawność programów i weryfikacja Poprawność programów Dowodzenie poprawności Wyspecyfikowany program Logika Hoare'a Definicje formalne Definicje formalne, c.d. Semantyka logiki Hoare'a Reguły wnioskowania Przykład dowodu Przykład dowodu, c.d. Niezmiennik pętli Przykład dowodu, c.d. W pełni wyspecyfikowany program Teorie pierwszego rzędu
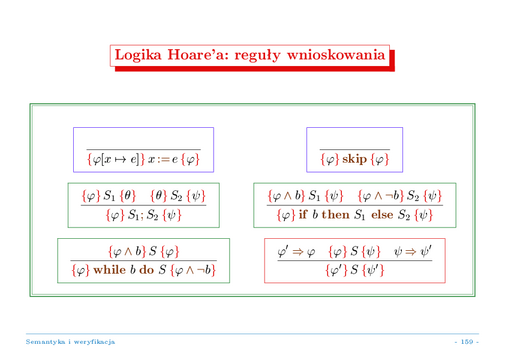
Na poprzednim slajdzie podaliśmy formalną semantyczną definicję spełniania stwierdzeń o częściowej poprawności programów. Jak wspomnieliśmy wcześniej, taka definicja wymaga uzupełnienia przez podanie metod dowodzenia wprowadzonych stwierdzeń o poprawności programów. Dla logiki Hoare'a służy temu formalny system dowodzenia stwierdzeń częściowej poprawności zadany regułami dowodzenia na powyższym slajdzie.
Po pierwsze, mamy tu reguły dla poszczególnych konstrukcji budujących instrukcje języka TINY.
Reguła dla instrukcji przypisania pozwala pokazać częściową poprawność instrukcji przypisania względem warunku wstępnego, mówiącego o wyrażeniu podstawianym na zmienna i warunku końcowego, który mówi to samo o zmiennej, na którą wykonano przypisanie.
Reguła dla instrukcji pustej pozwala pokazać częściową poprawność instrukcji pustej względem tych samych warunków wstępnego i końcowego.
Reguła dla instrukcji złożonej pozwala wyprowadzić częściową poprawność instrukcji złożonej względem danych warunków wstępnego i końcowego z częściowej poprawności składowych z warunkiem pośrednim jako warunkiem końcowym dla pierwszej składowej i warunkiem wstępnym dla składowej drugiej. Uwaga: stosowanie tej reguły dla pokazania częściowej poprawności instrukcji złożonej względem zadanych warunków wstępnego i końcowego wymaga oczywiście "wymyślenia" odpowiedniego warunku pośredniego.
Reguła dla instrukcji warunkowej pozwala wyprowadzić częściową poprawność tej instrukcji względem warunków wstępnego i końcowego z częściowej poprawności gałęzi instrukcji warunkowej względem odpowiednio wzmocnionych warunków wstępnych (o wyrażenie logiczne z warunku wyboru dla instrukcji lub jego negację, w zależności od rozważanej gałęzi) i tego samego warunku końcowego.
Reguła dla instrukcji pętli posługuje się warunkiem, zwanym "niezmiennikiem pętli", który ma zachodzić przy każdym sprawdzeniu warunku wejścia do ciała pętli, po kolejnych iteracjach tego ciała. Formalnie, przesłanka reguły wymaga, by ciało pętli było częściowo poprawne względem warunku wstępnego, który wzmacnia niezmiennik pętli o warunek wejścia do ciała pętli, i warunku końcowego, który jest po prostu niezmiennikiem ciała pętli. Reguła dla instrukcji pętli pozwala wyprowadzić z takiej przesłanki częściową poprawność całej instrukcji pętli względem niezmiennika jako warunku wstępnego i niezmiennika wzmocnionego o negację warunku wejście do ciała pętli jako warunku końcowego.
Ostatnia reguła, "reguła wynikania", nie jest związana z żadną konstrukcją językową; jest to więc niejako reguła "strukturalna", odpowiadająca podstawowej własności pojęcia poprawności: warunek wstępny zawsze można wzmocnić, a warunek końcowy zawsze można osłabić --- taka modyfikacja warunków wstępnego i końcowego zachowuje częściową poprawność instrukcji względem nich. Wykorzystanie tej reguły jest niezbędne, choćby dla "uzgodnienia" warunków na przykład w przesłankach reguły dla instrukcji złożonej, czy w przesłance dla instrukcji pętli.