PEE Moduł 9

|
Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów |
|
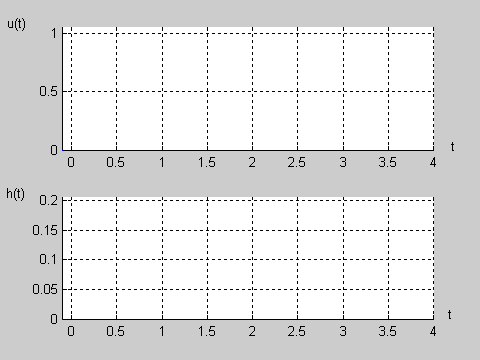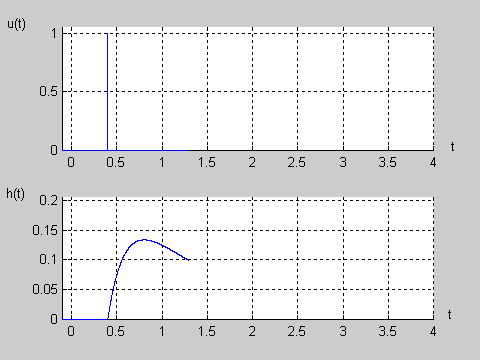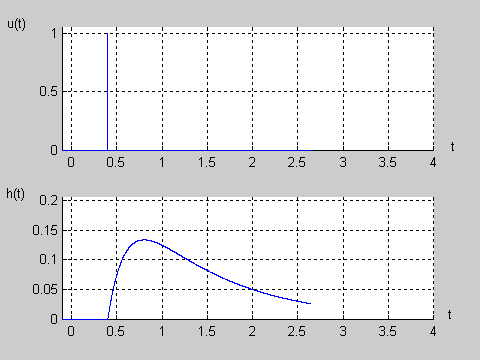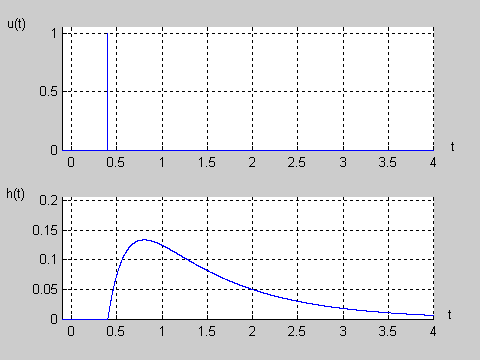
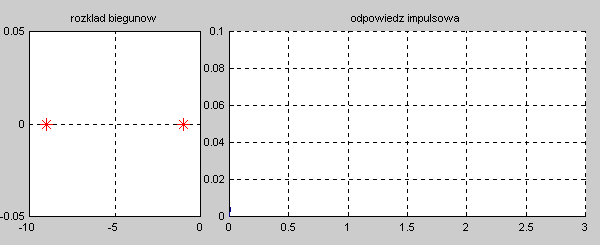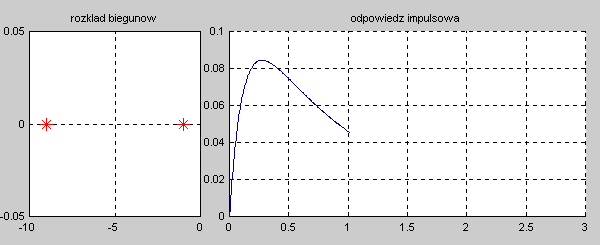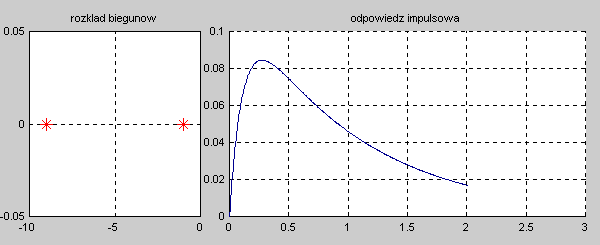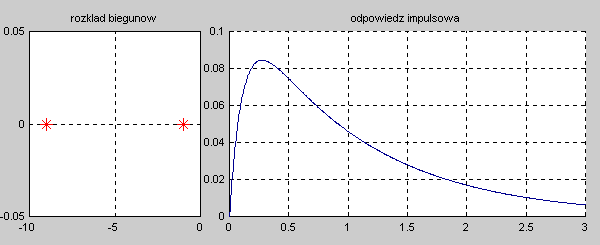
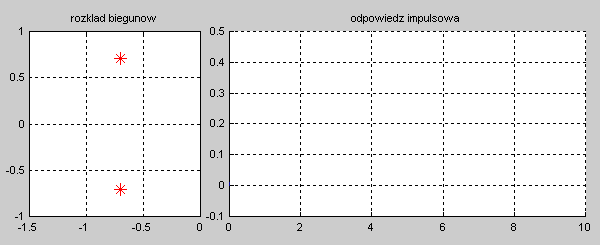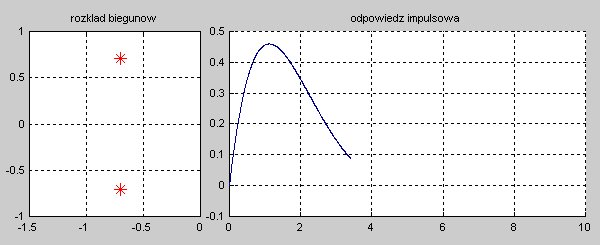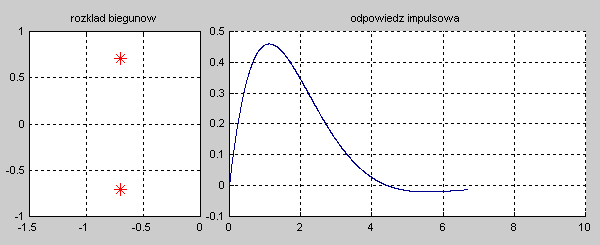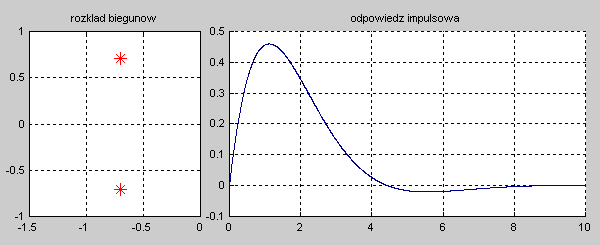
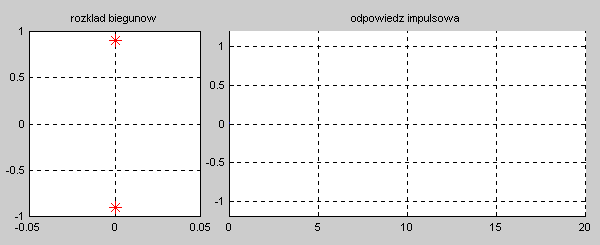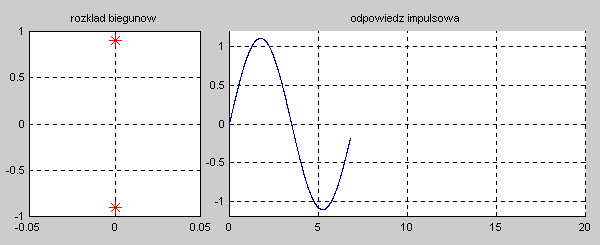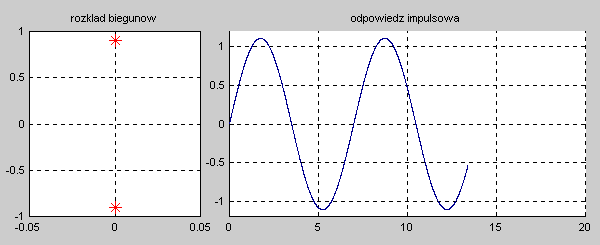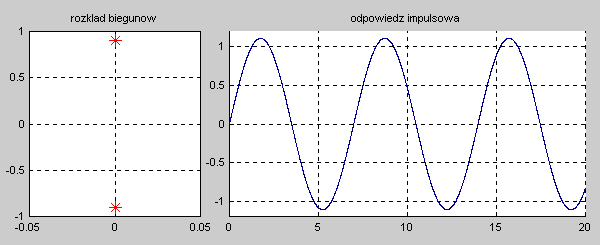
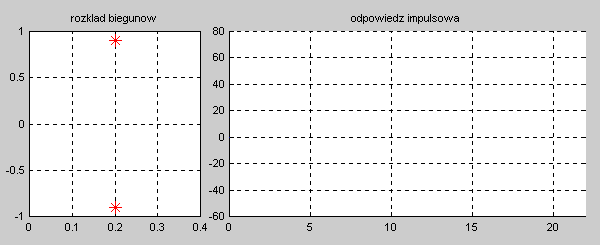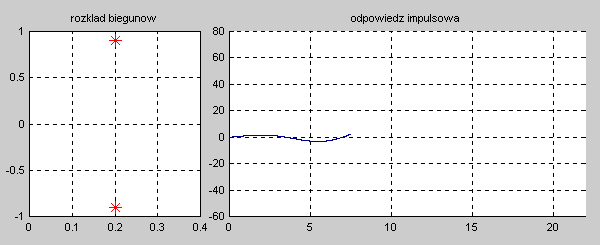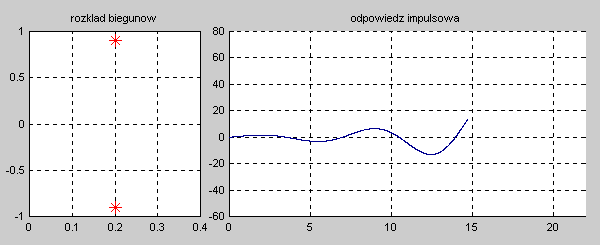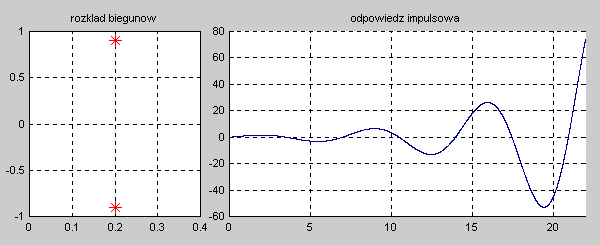
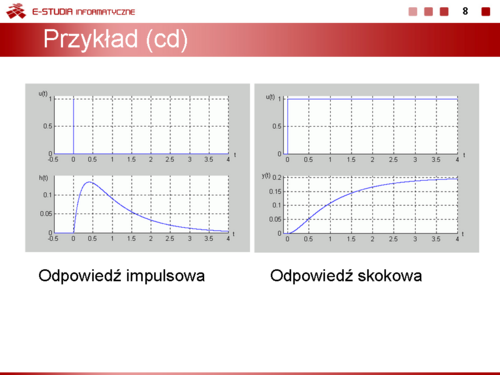
Na slajdzie obok i animacjach poniżej przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej . |

|
Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem
Załączony do podręcznika program interakcyjny CHARAKTERYSTYKI umożliwia wykreślanie charakterystyk częstotliwościowych (amplitudowych i fazowych) układów opisanych za pomocą transmitancji operatorowej o postaci określonej wzorem powyższym. Transmitancja widmowa takiego układu wyznaczana jest z transmitancji operatorowej , przez podstawienie . W wyniku otrzymuje się Transmitancja widmowa przedstawia sobą funkcję zespoloną pulsacji i może być zapisana w postaci ogólnej jako Część rzeczywista i urojona są funkcjami zarówno współczynników , licznika i mianownika transmitancji operatorowej, jak i aktualnej wartości pulsacji ,. Charakterystyka amplitudowa przedstawia sobą moduł transmitancji widmowej określony wzorem Charakterystyka fazowa jest fazą transmitancji widmowej i wyznaczana jest z zależności |
| <applet code="filtr.class" archive="images/6/6a/PEE_M9_filtr.jar" width="462" height="363">
</applet> |
Omawiane zależności zostały wykorzystane do badania charakterystyk częstotliwościowych układów opisanych transmitancją operatorową zadawaną przez użytkownika.
Użytkownik ustala stopień licznika i mianownika transmitancji, a także wartości wszystkich współczynników wielomianu licznika i mianownika. Określa również zakres pulsacji, dla którego wykreślane będą charakterystyki częstotliwościowe. W programie założono, że maksymalny rząd układu nie powinien przekroczyć wartości 9. Wykorzystując podane wcześniej zależności częstotliwościowe program wykreśla charakterystyki amplitudowe (liniową i logarytmiczną wyrażoną w decybelach) oraz charakterystykę fazową w stopniach. Charakterystyki filtru zostają wykreślone w oddzielnych oknach, pozwalających na skalowanie oraz oglądanie w powiększeniu poszczególnych odcinków krzywych. |
|
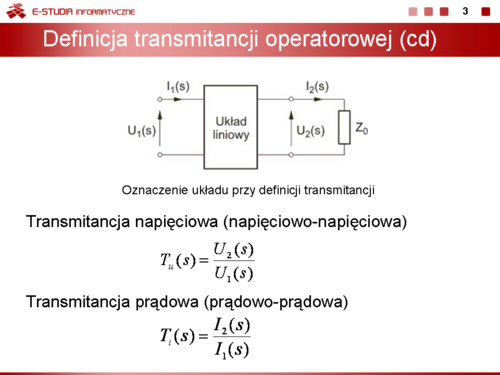
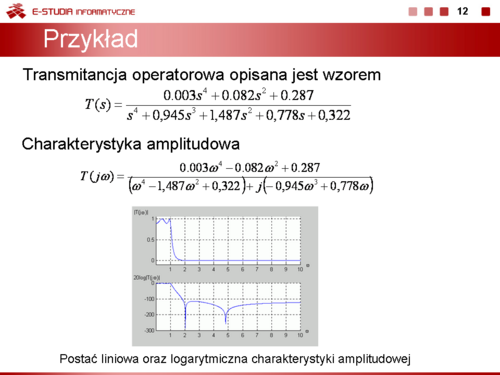
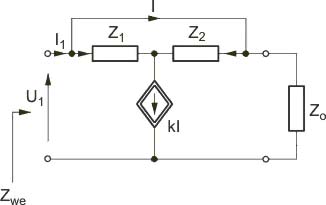
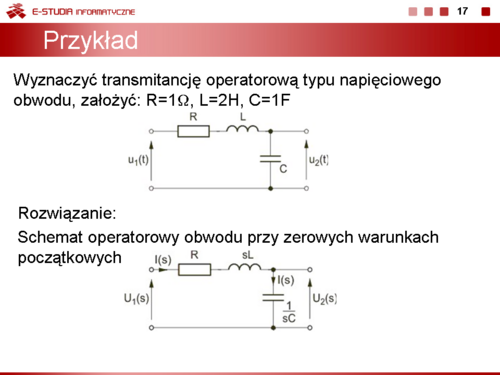
Jako przykład wyznaczymy transmitancję operatorową typu napięciowego obwodu (górny rysunek na slajdzie obok). Przyjmijmy: , ,, ,.
|

|
Kolejne etapy wyznaczania transmitancji:
Prąd I(s) Napięcie wyjściowe Transmitancja napięciowa Po podstawieniu wartości liczbowych otrzymuje się |
| Zadania sprawdzające
Wyznaczyć impedancję wejściową w postaci operatorowej dla obwodu przedstawionego na poniższym rysunku. Impedancję wejściową potraktować jako transmitancję napięciowo-prądową.
Rozwiązanie Z prawa prądowego i napięciowego Kirchhoffa napisanych dla obwodu z powyzszego rysunku otrzymuje się
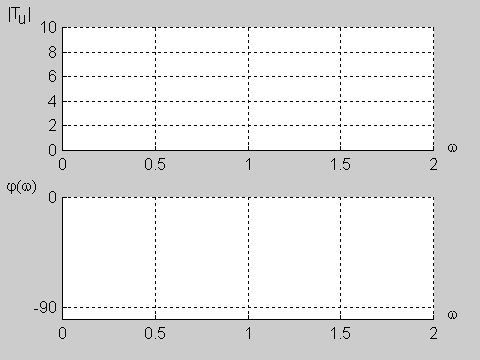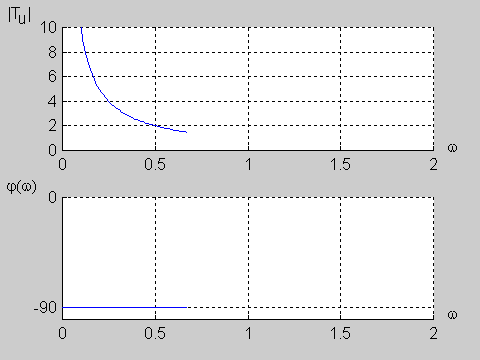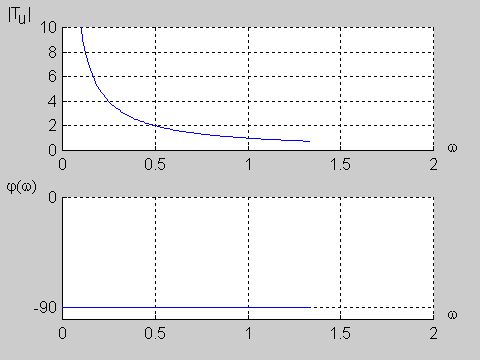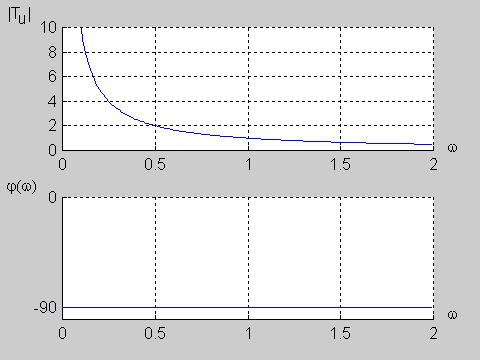
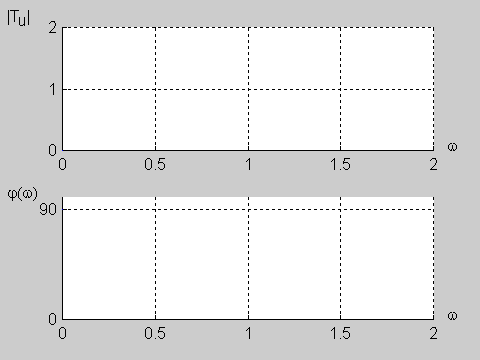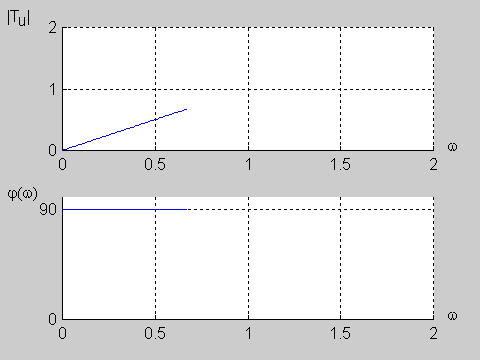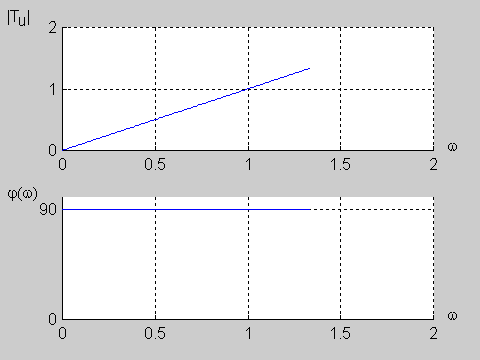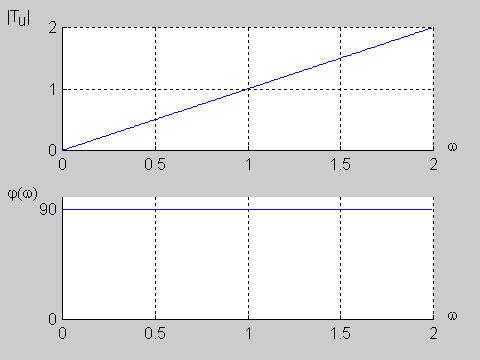
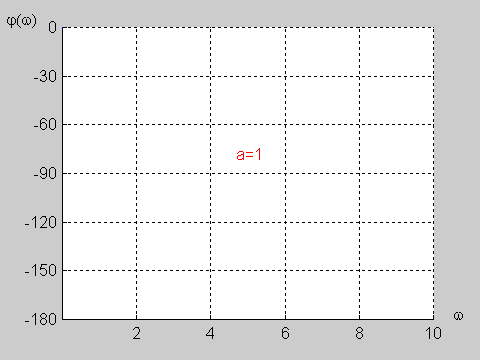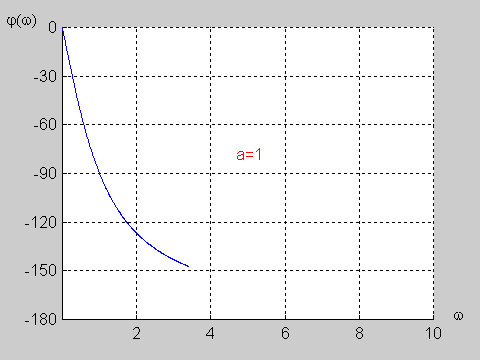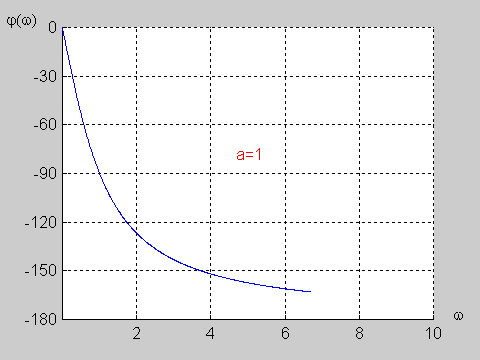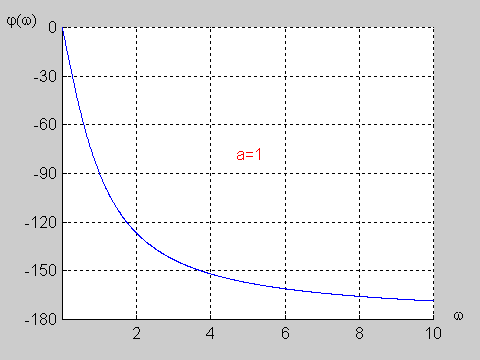
Zadanie 9.2 Wyznaczyć charakterystyki częstotliwościowe obwodu przedstawionego na poniższym rysunku biorąc pod uwagę transmitancję napięciową.
Transmitancja napięciowa obwodu określona jest wzorem
|