MO Moduł 1
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
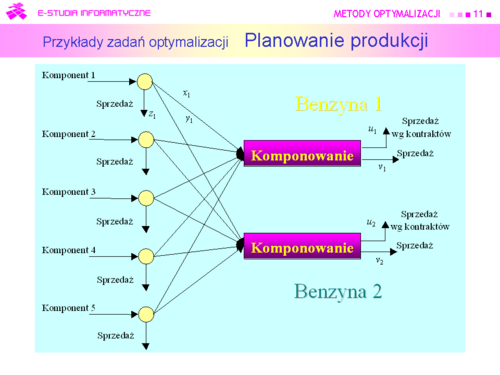
Współczynniki i można traktować dla benzyn np. jako liczbę oktanową. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
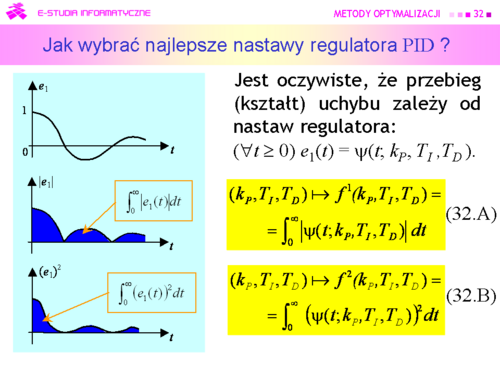 |
Zatem do oceny "odległości od zera” uchybu możemy posłużyć się całką z modułu uchybu (32.A), albo całką z kwadratu uchybu (32.B). |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Przypadku nie wykluczamy. |
 |
 |
 |
 |
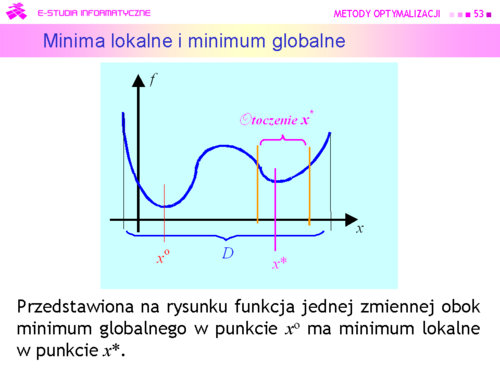 |
 |
 |
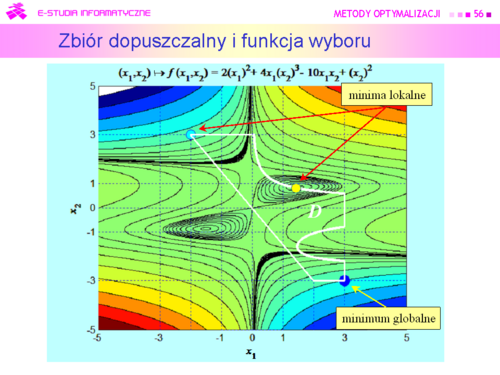 |
 |
 |
 |
 |
 |
 |
 |
 |
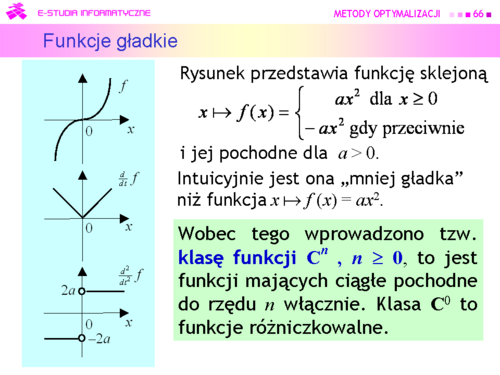 |
 |
 |
 |
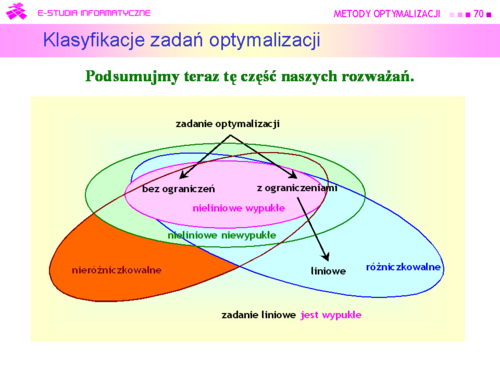 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Niepodzielny produkt to np. lodówka, lub lokówka, ale także paleta z kubeczkami jogurtu. |
 |
 |
 |
 |
Ograniczenia (85.C) mogliśmy zapisać w takiej postaci, bo jeżeli w miejscu nie zostanie wybudowana nowa fabryka to, , zatem na mocy (85.A) i (85.B), dla każdego wielkość przewozu . |
 |
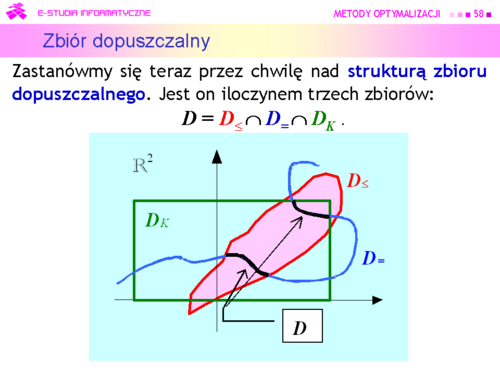
Są to związki logiczne a nie nierówności. Nie pasują zatem do przyjętego sposobu określania zbioru dopuszczalnego! |
 |
 |
 |
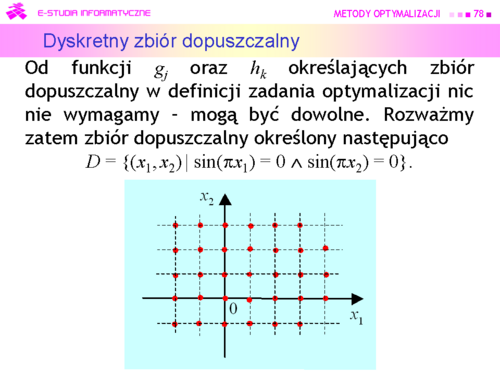
Przez oznaczono zbiór liczb całkowitych tj. zbiór . |
 |
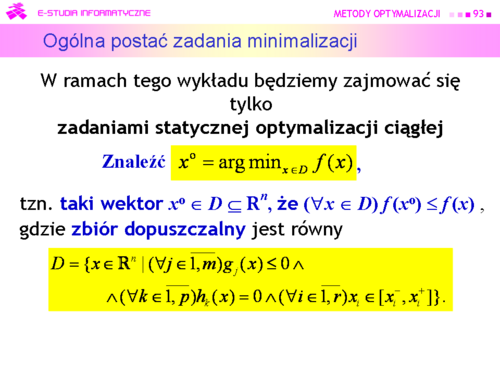 |