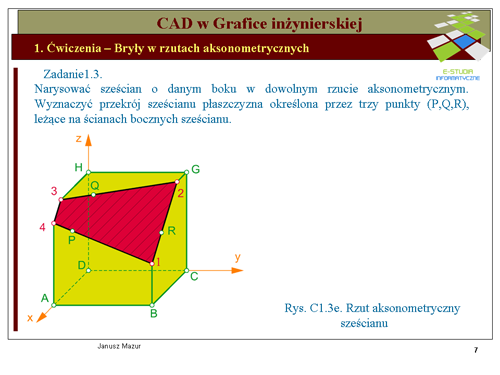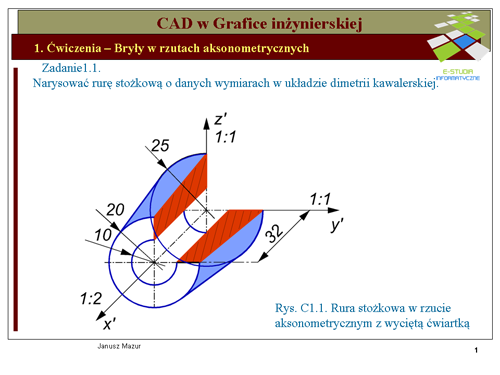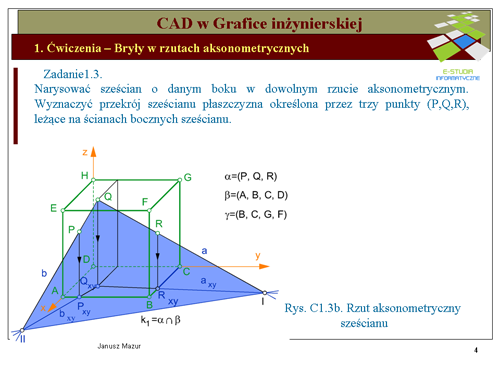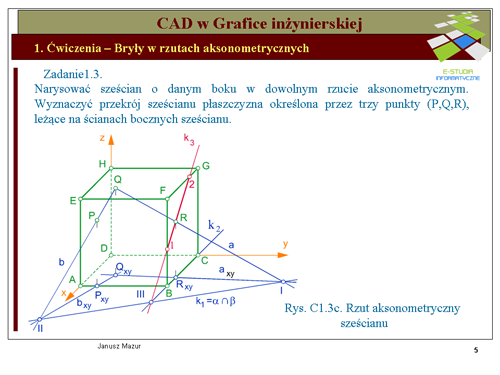
|
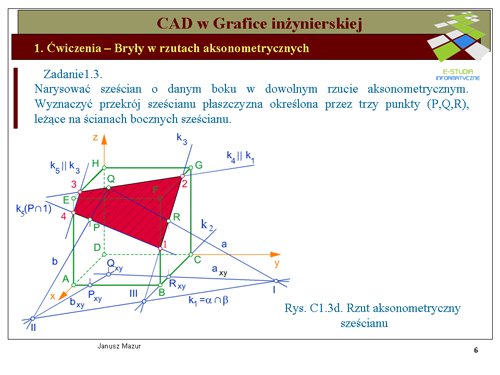
Zadanie1.2.
Narysować czworościan foremny o danym boku a, w układzie dimetrii kawalerskiej
Czworościan foremny jest bryłą, której wszystkie ściany są trójkątami równobocznymi (przyjmujemy wielkość boku a = 50 mm). Na rysunku C1.2. przedstawiono, po prawej stronie, trójkąt ABC, który jest podstawą tego czworościanu. Wyznaczając wysokości trójkąta, można wyznaczyć spodek wysokości czworościanu, a następnie budując trójkąt prostokątny w oparciu o znaną przyprostokątną (2/3 wysokości trójkąta - ,) oraz przeciwprostokątną , - krawędź , czworościanu) otrzymamy wszystkie jego wielkości geometryczne, niezbędne do budowy bryły w układzie aksonometrycznym, a w szczególności wysokość , czworościanu będącą rzeczywista wielkością odcinka ,.
Rozwiązanie zadania rozpoczynamy od wykreślenia układu aksonometrycznego - perspektywy kawalerskiej. Przypominając, w osiach , i ,, skrót aksonometryczny wynosi 1:1, natomiast w osi , wynosi 1:2. Podstawę czworościanu wykreślimy przyjmując w niezmienionej wielkości wysokość , podstawy i umieszczając ją równolegle do osi ,, przyjmując w pierwszej kolejności spodek wysokości , w dowolnym punkcie na osi ,. Bok ,, prostopadły do wysokości ,, przyjmie kierunek osi ,. Wielkość boku , będzie oczywiście o połowę mniejsza od rzeczywistej, ponieważ skrót aksonometryczny w kierunku tej osi wynosi 1:2. Ze spodka wysokości w niezmienionej wielkości wykreślamy wysokość czworościanu, wyznaczając wierzchołek , czworościanu. Łącząc wierzchołek , czworościanu z wierzchołkami , wyznaczymy zarys bryły. Na zakończenie należy uwzględnić widoczność krawędzi obserwując bryłę z kierunku prostopadłego do płaszczyzny określonej osiami ,. Krawędzie widoczne rysuje się linią grubą ciągłą, krawędzie niewidoczne linią
|