Analiza matematyczna 2/Ćwiczenia 9: Twierdzenie o funkcjach uwikłanych. Ekstrema warunkowe

Twierdzenie o funkcjach uwikłanych

Ćwiczenie 9.1.

W otoczeniu jakich punktów istnieje jednoznacznie określona funkcja

a) $x=x(y)$ rozwikłująca równanie $F(x,y)=x^2+2xy-y^2-a^2=0$ ($a\ne 0)$,

b) $y=y(x)$ rozwikłująca równanie $F(x,y)=\ln (\sqrt{x^2+y^2})-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}(\frac{y}{x})=0$,

c) $y=y(x)$ rozwikłująca równanie $F(x,y)=y^x-y+1=0$,

d) $z=z(x,y)$ rozwikłująca równanie $F(x,y,z)=xy+yz+zx=0$?

Wskazówka

Wykorzystać twierdzenie o funkcjach uwikłanych.

Rozwiązanie

a) Obliczmy pochodną cząstkową

$\frac{\partial F}{\partial x}=2x+2y$

Punkty, w których otoczeniu nie można rozwikłać równania względem zmiennej $x$, są określone przez układ równań

$\{\begin{array}{ll}& 2x+2y=0\\ & x^2+2xy-y^2-a^2=0.\\ \end{array}$

Wstawiając $x=-y$ do drugiego równania, otrzymujemy $-2x^2=a^2$. Z tego wynika, że powyższy układ nie ma rozwiązań. Tak więc nasze równanie można rozwikłać względem zmiennej $x$ w pewnym otoczeniu dowolnego punktu.

b) Rozumujemy podobnie jak w poprzednim przykładzie. Obliczmy pochodną cząstkową

$\frac{\partial F}{\partial y}=\frac{y-x}{x^2+y^2}$

Punkty, w których otoczeniu nie można rozwikłać równania względem zmiennej $y$, są określone przez układ równań

$\{\begin{array}{ll}& \frac{y-x}{x^2+y^2}=0\\ & \ln (\sqrt{x^2+y^2})-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}(\frac{y}{x})=0.\\ \end{array}$

Z pierwszego równania dostajemy $x=y$. Podstawiając tę zależność do drugiego równania, otrzymujemy $\frac{1}{2}\ln 2+\ln |x|=\frac{\pi }{4}$. Wynika stąd, że naszego równania nie można rozwikłać względem zmiennej $y$ w żadnym otoczeniu punktu $(x,y)$, tylko jeśli $(x,y)=(b,b)$ albo $(x,y)=(-b,-b)$, gdzie $b=e^{\frac{\pi }{4}-\frac{1}{2}\ln 2}$.

c) Obliczmy pochodną cząstkową

$\frac{\partial F}{\partial y}=x{y}^{x-1}-1$

Punkty, w których otoczeniu nie można rozwikłać równania względem zmiennej $y$, są określone przez układ równań

$\{\begin{array}{ll}& x{y}^{x-1}-1=0\\ & y^x+1-y=0.\\ \end{array}$

Z pierwszego równania dostajemy $y^{x-1}=\frac{1}{x}$. Podstawiając tę zależność do drugiego równania, otrzymujemy $\frac{y}{x}+1=y$, czyli $x=\frac{y}{y-1}$. Podstawiając otrzymany wzór do drugiego równania, dostajemy

$y^{\frac{y}{y-1}}+1-y=0$,

czyli

$(y-1{)}^{y-1}=y^y$

Zauważmy, że nasze wyjściowe równanie $y^x+1=y$ jest określone dla $y>1$, gdyż lewa strona tego równania jest większa od jedności. Aby rozwiązać równanie $(y-1{)}^{y-1}=y^y$, rozważmy funkcję $f(x)=x^x$. Jej pochodna wynosi $f^{\prime }(x)=x^x(1+\ln x)>0$, czyli $f$ jest silnie rosnąca. Stąd wynika, że równanie $(y-1{)}^{y-1}=y^y$ nie ma rozwiązań. Zatem równanie $y=1+y^x$ można rozwikłać względem zmiennej $y$ w pewnym otoczeniu każdego punktu.

d) Obliczmy pochodną cząstkową

$\frac{\partial F}{\partial z}=y+x$

Punkty, w których otoczeniu nie można rozwikłać równania względem zmiennej $z$, są określone przez układ równań

$\{\begin{array}{ll}& y+x=0\\ & xy+yz+zx=0.\\ \end{array}$

Z pierwszego równania dostajemy $x=-y$. Podstawiając tę zależność do drugiego równania, otrzymujemy $-x^2=0$, czyli $x=y=0$. Z tego wynika, że naszego równania nie można rozwikłać względem zmiennej $z$ w żadnym otoczeniu dowolnego punktu postaci $(0,0,z)$.

Ćwiczenie 9.2.

Zapisać poniższe równania we współrzędnych biegunowych. W otoczeniu jakich punktów istnieje jednoznacznie określona funkcja $y=y(x)$ rozwikłująca równanie

a) $F(x,y)=(x^2+y^2{)}^2-2a^2(x^2-y^2)=0(a\ne 0)$,

b) $F(x,y)=(x^2+y^2-a^2{)}^3+27a^2{x}^2{y}^2=0(a\ne 0)$,

c) $F(x,y)=x^3+y^3-3axy=0$?

Wskazówka

Wykorzystać twierdzenie o funkcjach uwikłanych.

Rozwiązanie

Rysunek do ćwiczenia 9.2.(a)

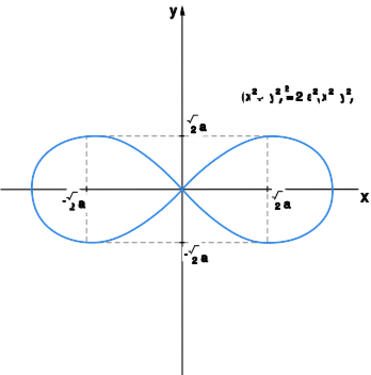
a) Równanie $F(x,y)=(x^2+y^2{)}^2-2a^2(x^2-y^2)=0$ opisuje krzywą zwaną lemniskatą Bernoullego. Obliczmy pochodną cząstkową

$\frac{\partial F}{\partial y}=4y(x^2+y^2)+4y{a}^2=4y(x^2+y^2+a^2)$

Punkty, w których otoczeniu nie można rozwikłać równania względem zmiennej $y$, są określone przez układ równań

$\{\begin{array}{ll}& y=0\\ & (x^2+y^2{)}^2-2a^2(x^2-y^2)=0.\\ \end{array}$

Podstawiając $y=0$ do drugiego równania, otrzymujemy $x^4=2a^2{x}^2$, czyli $x=0$ lub $x=\sqrt{2}a$ lub $x=-\sqrt{2}a$. Wynika z tego, że naszego równania nie można rozwikłać względem zmiennej $y$ w żadnym otoczeniu punktu $(x,y)$, tylko jeśli $x\in \{0,\sqrt{2}a,-\sqrt{2}a\}$ i $y=0$. Widać to na rysunku

Znajdziemy teraz równanie leminiskaty Bernoullego we współrzędnych biegunowych. Podstawiając do równania $(x^2+y^2{)}^2-2a^2(x^2-y^2)=0$ zmienne $x=r\cos \phi$ i $y=r\sin \phi$, dostajemy równanie

$r^4=2a^2{r}^2({\cos }^2\phi -{\sin }^2\phi )$,

czyli

$r^2=2a^2\cos (2\phi )$

Rysunek do ćwiczenia 9.2.(b)

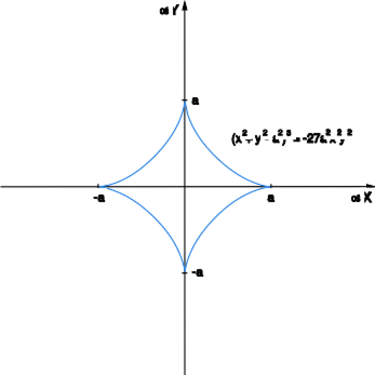
b) Równanie $F(x,y)=(x^2+y^2-a^2{)}^3+27a^2{x}^2{y}^2=0$ lub równoważne $x^2+y^2-a^2=-3a^{\frac{2}{3}}{x}^{\frac{2}{3}}{y}^{\frac{2}{3}}$ opisuje krzywą zwaną asteroidą. Zapiszemy to równanie w równoważnej, jeszcze prostszej postaci:

$\begin{array}{rl}& 0=x^2+y^2-a^2+3a^{\frac{2}{3}}{x}^{\frac{2}{3}}{y}^{\frac{2}{3}}\\ & ={(x^{\frac{2}{3}}+y^{\frac{2}{3}})}^3-{\left(a^{\frac{2}{3}}\right)}^3-3x^{\frac{4}{3}}{y}^{\frac{2}{3}}-3x^{\frac{2}{3}}{y}^{\frac{4}{3}}+3a^{\frac{2}{3}}{x}^{\frac{2}{3}}{y}^{\frac{2}{3}}\\ & =(x^{\frac{2}{3}}+y^{\frac{2}{3}}-a^{\frac{2}{3}})({(x^{\frac{2}{3}}+y^{\frac{2}{3}})}^2+a^{\frac{2}{3}}(x^{\frac{2}{3}}+y^{\frac{2}{3}})+a^{\frac{4}{3}}-3x^{\frac{2}{3}}{y}^{\frac{2}{3}})\\ & =(x^{\frac{2}{3}}+y^{\frac{2}{3}}-a^{\frac{2}{3}})({(x^{\frac{2}{3}}-y^{\frac{2}{3}})}^2+a^{\frac{2}{3}}(x^{\frac{2}{3}}+y^{\frac{2}{3}})+a^{\frac{4}{3}}+x^{\frac{2}{3}}{y}^{\frac{2}{3}}).\end{array}$

Zauważmy, że wyrażenie

${(x^{\frac{2}{3}}-y^{\frac{2}{3}})}^2+a^{\frac{2}{3}}(x^{\frac{2}{3}}+y^{\frac{2}{3}})+a^{\frac{4}{3}}+x^{\frac{2}{3}}{y}^{\frac{2}{3}}\ge a^{\frac{4}{3}}>0$,

czyli równanie asteroidy jest równoważne równaniu

$G(x,y)=x^{\frac{2}{3}}+y^{\frac{2}{3}}-a^{\frac{2}{3}}=0$

Obliczmy pochodną cząstkową

$\frac{\partial G}{\partial y}=\frac{2}{3}{y}^{-\frac{1}{3}}$

Z tego wynika, że naszego równania nie można rozwikłać względem zmiennej $y$ w żadnym otoczeniu punktu$(a,0)$ ani w żadnym otoczeniu punktu $(-a,0)$. Widać to na rysunku

Znajdziemy teraz równanie asteroidy we współrzędnych biegunowych.

Podstawiając do równania $(x^2+y^2-a^2{)}^3+27a^2{x}^2{y}^2=0$

zmienne $x=r\cos \phi$ i $y=r\sin \phi$, dostajemy równanie

$(r^2-a^2{)}^3=-27a^2{r}^4{\cos }^2\phi {\sin }^2\phi$,

czyli

$r^2=-\frac{3}{\sqrt[3]{4}}{a}^{\frac{2}{3}}{r}^{\frac{4}{3}}{\sin }^{\frac{2}{3}}(2\phi )+a^2$

Rysunek do ćwiczenia 9.2.(c)

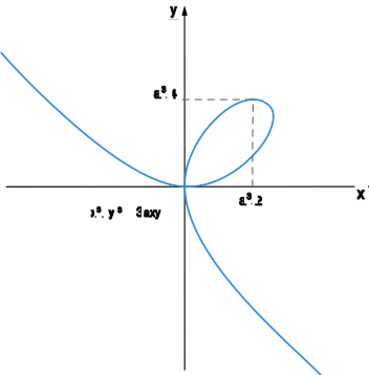
c) Równanie $F(x,y)=x^3+y^3-3axy=0$ opisuje krzywą zwaną liściem Kartezjusza. Obliczmy pochodną cząstkową

$\frac{\partial F}{\partial y}=3y^2-3ax$

Punkty, w których otoczeniu nie można rozwikłać równania względem zmiennej $y$ są określone przez układ równań

$\{\begin{array}{ll}& 3y^2-3ax=0\\ & x^3+y^3-3axy=0.\\ \end{array}$

Z pierwszego równania dostajemy $x=\frac{y^2}{a}$. Podstawiając to wyrażenie do drugiego równania, otrzymujemy $\frac{y^6}{a^3}-2y^3=0$, czyli $y=0$ lub $y=\sqrt[3]{2}a$. Wynika z tego, że naszego równania nie można rozwikłać względem zmiennej $y$ w żadnym otoczeniu punktu $(0,0)$ ani w żadnym otoczeniu punktu $(\sqrt[3]{4}a,\sqrt[3]{2}a)$. Widać to na rysunku

Znajdziemy teraz równanie liścia Kartezjusza we współrzędnych biegunowych. Podstawiając do równania $x^3+y^3-3axy=0$ zmienne $x=r\cos \phi$ i $y=r\sin \phi$, dostajemy równanie

$r^3({\cos }^3\phi +{\sin }^3\phi )=3a{r}^2\cos \phi \sin \phi$,

czyli

$r=\frac{3}{2}a\frac{\sin (2\phi )}{{\cos }^3\phi +{\sin }^3\phi }$

Ćwiczenie 9.3.

a) Obliczyć pierwszą i drugą pochodną funkcji $y=y(x)$ w punkcie $e$, jeśli $y(e)=1$ i funkcja $y=y(x)$ jest uwikłana równaniem $F(x,y)=x^{2}y-e^{2y}=0$.

b) Obliczyć pierwszą i drugą pochodną funkcji $y=y(x)$ w punkcie $-1$, jeśli $y(-1)=-1$ i funkcja $y=y(x)$ jest uwikłana równaniem $F(x,y)=y{e}^x+e^y=0$.

c) Obliczyć pochodne cząstkowe rzędu pierwszego i drugiego funkcji $z=z(x,y)$ w punkcie $(2,1)$, jeśli $z(2,1)=0$ i funkcja $z=z(x,y)$ jest uwikłana równaniem $F(x,y,z)=e^z-xyz-1=0$.

d) Obliczyć pochodne cząstkowe rzędu pierwszego i drugiego funkcji $z=z(x,y)$ w punkcie $(0,\frac{\pi }{4})$, jeśli $z(0,\frac{\pi }{4})=\frac{\pi }{4}$ i funkcja $z=z(x,y)$ jest uwikłana równaniem $F(x,y,z)=x+\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}(\frac{y}{z-x})-z=0$.

Wskazówka

Wykorzystać twierdzenie o funkcjach uwikłanych. Jaki jest związek między pochodnymi cząstkowymi funkcji $F$, a pochodną funkcji $y$ czy $z$?

Rozwiązanie

a) Ponieważ $F(e,1)=0$ oraz

$\frac{\partial F}{\partial y}=x^2-2e^{2y},\frac{\partial F}{\partial y}(e,1)=-e^2\ne 0$,

więc w otoczeniu punktu $e$ istnieje funkcja $y=y(x)$ (taka, że $y(e)=1$) rozwikłująca równanie $F(x,y)=x^{2}y-e^{2y}=0$. Obliczmy pochodną cząstkową funkcji $F$ względem zmiennej $x$. Mamy

$\frac{\partial F}{\partial x}=2xy,\frac{\partial F}{\partial x}(e,1)=2e$

Stąd pochodna funkcji $y(x)$ jest równa

$y^{\prime }(x)=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}=-\frac{2xy}{x^2-2e^{2y}}$,

czyli $y^{\prime }(e)=\frac{2}{e}$. Pamiętając, że $y=y(x)$, obliczamy drugą pochodną

$y^{″}(x)=\frac{(2y+2x{y}^{\prime })(2e^{2y}-x^2)-2xy(4e^{2y}{y}^{\prime }-2x)}{(2e^{2y}-x^2{)}^2}$,

a stąd $y^{″}(e)=-\frac{6}{e^2}$.

b) Ponieważ $F(-1,-1)=0$ oraz

$\frac{\partial F}{\partial y}=e^x+e^y,\frac{\partial F}{\partial y}(-1,-1)=2e^{-1}\ne 0$,

więc w otoczeniu punktu $-1$ istnieje funkcja $y=y(x)$ (taka, że $y(-1)=-1$) rozwikłująca równanie $F(x,y)=y{e}^x+e^y=0$. Obliczmy pochodną cząstkową funkcji $F$ względem zmiennej $x$. Mamy

$\frac{\partial F}{\partial x}=y{e}^x,\frac{\partial F}{\partial x}(-1,-1)=-e^{-1}$

Stąd pochodna funkcji $y(x)$ jest równa

$y^{\prime }(x)=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}=-\frac{y{e}^x}{e^x+e^y}$,

czyli $y^{\prime }(-1)=-\frac{1}{2}$. Pamiętając, że $y=y(x)$, obliczmy drugą pochodną

$y^{″}(x)=-\frac{(y^{\prime }{e}^x+y{e}^x)(e^x+e^y)-y{e}^x(e^x+y^{\prime }{e}^y)}{(e^x+e^y{)}^2}$,

a stąd $y^{″}(-1)=\frac{5}{8}$.

c) Ponieważ $F(2,1,0)=0$ oraz

$\frac{\partial F}{\partial z}=e^z-xy,\frac{\partial F}{\partial z}(2,1,0)=-1\ne 0$,

więc w otoczeniu punktu $(2,1)$ istnieje funkcja $z=z(x,y)$ (taka, że $z(2,1)=0$) rozwikłująca równanie $F(x,y,z)=e^z-xyz-1=0$. Obliczmy pochodne cząstkowe funkcji $F$ względem zmiennych $x$ i $y$. Mamy

$\begin{array}{rl}& \frac{\partial F}{\partial x}=-yz,\frac{\partial F}{\partial x}(2,1,0)=0,\\ & \frac{\partial F}{\partial y}=-xz,\frac{\partial F}{\partial y}(2,1,0)=0.\end{array}$

Stąd pochodne cząstkowe funkcji $z(x,y)$ są równe

$\begin{array}{rl}& \frac{\partial z}{\partial x}=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}}=\frac{yz}{e^z-xy},\frac{\partial z}{\partial x}(2,1)=0,\\ & \frac{\partial z}{\partial y}=-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}}=\frac{xz}{e^z-xy},\frac{\partial z}{\partial y}(2,1)=0.\end{array}$

Pamiętając, że $z=z(x,y)$, obliczmy pochodne cząstkowe rzędu drugiego

$\begin{array}{rl}& \frac{{\partial }^{2}z}{\partial x^2}=\frac{(y\frac{\partial z}{\partial x})(e^z-xy)-yz(\frac{\partial z}{\partial x}{e}^z-y)}{(e^z-xy{)}^2},\\ & \frac{{\partial }^{2}z}{\partial x\partial y}=\frac{(z+y\frac{\partial z}{\partial y})(e^z-xy)-yz(\frac{\partial z}{\partial y}{e}^z-x)}{(e^z-xy{)}^2},\\ & \frac{{\partial }^{2}z}{\partial y^2}=\frac{(x\frac{\partial z}{\partial y})(e^z-xy)-xz(\frac{\partial z}{\partial y}{e}^z-x)}{(e^z-xy{)}^2},\\ \end{array}$

a stąd wynika, że wszystkie pochodne rzędu drugiego funkcji $z$ w punkcie $(2,1)$ są równe zeru.

d) Ponieważ $F(0,\frac{\pi }{4},\frac{\pi }{4})=0$ oraz

$\frac{\partial F}{\partial z}=-\frac{(z-x{)}^2+y^2+y}{(z-x{)}^2+y^2},\frac{\partial F}{\partial z}(0,\frac{\pi }{4},\frac{\pi }{4})=-\frac{\pi +2}{\pi }\ne 0$,

więc w otoczeniu punktu $(0,\frac{\pi }{4})$ istnieje funkcja $z=z(x,y)$ (taka, że $z(0,\frac{\pi }{4})=\frac{\pi }{4}$) rozwikłująca równanie $F(x,y,z)=x-z+\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}(\frac{y}{z-x})=0$. Obliczmy pochodne cząstkowe funkcji $F$ względem zmiennych $x$ i $y$. Mamy

$\begin{array}{rl}& \frac{\partial F}{\partial x}=\frac{(z-x{)}^2+y^2+y}{(z-x{)}^2+y^2},\\ & \frac{\partial F}{\partial y}=\frac{z-x}{(z-x{)}^2+y^2}.\end{array}$

Stąd pochodne cząstkowe funkcji $z(x,y)$ są równe

$\begin{array}{rl}& \frac{\partial z}{\partial x}=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}}=-\frac{\frac{(z-x{)}^2+y^2+y}{(z-x{)}^2+y^2}}{-\frac{(z-x{)}^2+y^2+y}{(z-x{)}^2+y^2}}=1,\\ & \frac{\partial z}{\partial y}=-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}}=-\frac{\frac{z-x}{(z-x{)}^2+y^2}}{-\frac{(z-x{)}^2+y^2+y}{(z-x{)}^2+y^2}}=\frac{z-x}{(z-x{)}^2+y^2+y},\end{array}$

czyli

$\begin{array}{rl}& \frac{\partial z}{\partial x}(0,\frac{\pi }{4})=1\\ & \frac{\partial z}{\partial x}(0,\frac{\pi }{4})=\frac{2}{\pi +2}.\end{array}$

Pamiętając, że $z=z(x,y)$, obliczmy pochodne cząstkowe rzędu drugiego

$\begin{array}{rl}& \frac{{\partial }^{2}z}{\partial x^2}=0,\\ & \frac{{\partial }^{2}z}{\partial x\partial y}=0,\\ & \frac{{\partial }^{2}z}{\partial y^2}=\frac{\frac{\partial z}{\partial y}((z-x{)}^2+y^2+y)-(z-x)(2(z-x)\frac{\partial z}{\partial y}+2y+1)}{((z-x{)}^2+y^2+y{)}^2},\\ \end{array}$

a stąd wynika, że

$\begin{array}{rl}& \frac{{\partial }^{2}z}{\partial x^2}(0,\frac{\pi }{4})=0,\\ & \frac{{\partial }^{2}z}{\partial x\partial y}(0,\frac{\pi }{4})=0,\\ & \frac{{\partial }^{2}z}{\partial y^2}(0,\frac{\pi }{4})=-\frac{8(\pi +4)}{(\pi +2{)}^3}.\end{array}$

Ćwiczenie 9.4.

a) Rozważamy funkcje $y=y(x)$ i $z=z(x)$ określone układem równań

$\{\begin{array}{ll}& \ln y+y\ln z+xz=0\\ & x-y+z=0\\ \end{array}$

i takie, że $y(0)=z(0)=1$. Obliczyć pochodne $y^{\prime }(0)$ i $z^{\prime }(0)$.

b) Rozważamy funkcje $u=u(x,y)$ i $v=v(x,y)$ są uwikłane układem równań

$\{\begin{array}{ll}& x-e^u-u\sin v=0\\ & y-e^u-u\cos v=0\\ \end{array}$

i takie, że $u(e,e-1)=1$ i $v(e,e-1)=0$. Wyznaczyć pochodne cząstkowe rzędu pierwszego tych funkcji w punkcie $(e,e-1)$.

Wskazówka

Zróżniczkować każde równanie stronami i podstawić znane wartości w interesującym nas punkcie. Rozwiązać uzyskany układ równań, traktując szukane pochodne jako niewiadome.

Rozwiązanie

a) Różniczkujemy oba równania układu

$\{\begin{array}{ll}& \ln y+y\ln z+xz=0\\ & x-y+z=0\\ \end{array}$

stronami, pamiętając, że $y=y(x)$ i $z=z(x)$. Mamy

$\{\begin{array}{ll}& y^{\prime }\frac{1}{y}+y^{\prime }\ln z+y\frac{z^{\prime }}{z}+z+x{z}^{\prime }=0\\ & 1-y^{\prime }+z^{\prime }=0.\\ \end{array}$

W punkcie $(0,1,1)$ otrzymujemy układ równań

$\{\begin{array}{ll}& y^{\prime }(0)+z^{\prime }(0)=-1\\ & -y^{\prime }(0)+z^{\prime }(0)=-1\\ \end{array}$

Ostatecznie $y^{\prime }(0)=0$ i $z^{\prime }(0)=-1$.

b) Różniczkujemy po $x$ oba równania układu

$\{\begin{array}{ll}& x-e^u-u\sin v=0\\ & y-e^u-u\cos v=0\\ \end{array}$

stronami, pamiętając, że $u=u(x,y)$ i $v=v(x,y)$. Mamy

$\{\begin{array}{ll}& 1-\frac{\partial u}{\partial x}{e}^u-\frac{\partial u}{\partial x}\sin v-u\frac{\partial v}{\partial x}\cos v=0\\ & -\frac{\partial u}{\partial x}{e}^u-\frac{\partial u}{\partial x}\cos v+u\frac{\partial v}{\partial x}\sin v=0.\\ \end{array}$

W punkcie $(e,e-1,1,0)$ otrzymujemy układ równań

$\{\begin{array}{ll}& -e\frac{\partial u}{\partial x}(e,e-1)-\frac{\partial v}{\partial x}(e,e-1)=-1\\ & -(e+1)\frac{\partial u}{\partial x}(e,e-1)=0.\\ \end{array}$

Ostatecznie

$\begin{array}{rl}& \frac{\partial u}{\partial x}(e,e-1)=0,\\ & \frac{\partial v}{\partial x}(e,e-1)=1.\\ \end{array}$

Podobnie postępujemy, szukając pochodnych cząstkowych po $y$. Różniczkujemy po $y$ oba równania układu

$\{\begin{array}{ll}& x-e^u-u\sin v=0\\ & y-e^u-u\cos v=0\\ \end{array}$

stronami, pamiętając, że $u=u(x,y)$ i $v=v(x,y)$. Mamy

$\{\begin{array}{ll}& -\frac{\partial u}{\partial y}{e}^u-\frac{\partial u}{\partial y}\sin v-u\frac{\partial v}{\partial y}\cos v=0\\ & 1-\frac{\partial u}{\partial y}{e}^u-\frac{\partial u}{\partial y}\cos v+u\frac{\partial v}{\partial y}\sin v=0.\\ \end{array}$

W punkcie $(e,e-1,1,0)$ otrzymujemy układ równań

$\{\begin{array}{ll}& -e\frac{\partial u}{\partial y}(e,e-1)-\frac{\partial v}{\partial y}(e,e-1)=0\\ & 1-(e+1)\frac{\partial u}{\partial y}(e,e-1)=0.\\ \end{array}$

Ostatecznie

$\begin{array}{rl}& \frac{\partial u}{\partial y}(e,e-1)=\frac{1}{e+1},\\ & \frac{\partial v}{\partial y}(e,e-1)=-\frac{e}{e+1}.\\ \end{array}$

Ćwiczenie 9.5.

Rozważamy funkcję $y=y(x)$ uwikłaną równaniem $F(x,y)=xy+\ln x+\ln y-1=0$ i taką, że $y(1)=1$. Rozwinąć ją w szereg Taylora w punkcie $1$.

Wskazówka

Wykorzystać twierdzenie o funkcjach uwikłanych. Wyliczyć $y^{\prime }(1),y^{″}(1),y^{‴}(1)$, odgadnąć wzór na $y^{(n)}(1)$ i indukcyjnie wykazać, że jest prawdziwy. Zastosować wzór Taylora. Można także spróbować wyznaczyć jawny wzór na funkcję $y=y(x)$: podstawić $z=xy$ w równaniu $F(x,y)=0$ i rozwiązać to równanie z jedną niewiadomą.

Rozwiązanie

Ponieważ $F(1,1)=0$ oraz

$\frac{\partial F}{\partial y}=x+\frac{1}{y},\frac{\partial F}{\partial y}(1,1)=2\ne 0$,

a więc w otoczeniu punktu $1$ istnieje funkcja $y=y(x)$ (taka, że $y(1)=1$) rozwikłująca równanie $F(x,y)=xy+\ln x+\ln y-1=0$. Obliczmy pochodne funkcji $y(x)$ w punkcie $x=1$. Mamy

$\frac{\partial F}{\partial x}=y+\frac{1}{x}$,

czyli

$y^{\prime }(x)=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}=-\frac{y}{x}$

Udowodnimy indukcyjnie, że dla dowolnego $n$

$y^{(n)}=(-1{)}^{n}n!\frac{y}{x^n}$

Dla $n=1$ wzór jest prawdziwy. Załóżmy, że jest on prawdziwy dla liczby $n$. Wykażemy wtedy, że jest on również prawdziwy dla liczby $n+1$. Korzystając z założenia indukcyjnego i wzoru $y^{\prime }(x)=-\frac{y}{x}$, mamy

$\begin{array}{rl}& y^{(n+1)}(x)=\left(y^{(n)}\right)(x)=((-1{)}^{n}n!\frac{y}{x^n})=(-1{)}^{n}n!\frac{y^{\prime }{x}^n-n{x}^{n-1}y}{x^{2n}}\\ & =(-1{)}^{n}n!\frac{-y{x}^{n-1}-n{x}^{n-1}y}{x^{2n}}=(-1{)}^{n+1}(n+1)!\frac{y}{x^{n+1}}.\end{array}$

Stąd na mocy zasady indukcji matematycznej wzór jest prawdziwy dla każdego $n$. Obliczmy wartość pochodnych funkcji $y$ w punkcie $x=1$

$y^{(n)}(1)=(-1{)}^{n}n!\frac{y(1)}{1^n}=(-1{)}^{n}n!$

Stosując rozwinięcie Taylora, dostajemy

$y(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{y^{(n)}(1)}{n!}(x-1{)}^n=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^{n}n!}{n!}(x-1{)}^n=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n(x-1{)}^n$

Postaramy się teraz rozwiązać to zadanie inną metodą. Zauważmy, że podstawiając do równania $F(x,y)=xy+\ln x+\ln y-1=0$ nową zmienną $z=xy$, dostajemy równanie $z-1+\ln z=0$. Równanie to ma tylko jedno rozwiązanie $z=1$. Stąd wynika, że nasze wyjściowe równanie jest równoważne równaniu $xy=1$, czyli $y=\frac{1}{x}$. Szereg Taylora dla funkcji $y(x)=\frac{1}{x}$ można otrzymać, wykorzystując własności szeregu geometrycznego. Mamy w otoczeniu punktu $x=1$

$y(x)=\frac{1}{x}=\frac{1}{1+x-1}=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n(x-1{)}^n$

Ćwiczenie 9.6.

Znaleźć ekstrema funkcji uwikłanej

a) $y=y(x)$ określonej równaniem $F(x,y)=(x^2+y^2{)}^2-2a^2(x^2-y^2)=0(a\ne 0)$,

b) $y=y(x)$ określonej równaniem $F(x,y)=x^3+y^3-3axy=0(a\ne 0)$,

c) $z=z(x,y)$ określonej równaniem $F(x,y,z)=x^2+y^2+z^2-6z=0$,

d) $z=z(x,y)$ określonej równaniem $F(x,y,z)=x-z\ln (\frac{z}{y})=0$,

e) $z=z(x,y)$ określonej równaniem $F(x,y,z)=z^3-3xyz-20=0$.

Wskazówka

Wykorzystać twierdzenie o funkcjach uwikłanych. Następnie skorzystać z metod wyznaczania ekstremów dla funkcji jednej lub wielu zmiennych. Należy pamiętać o sprawdzaniu, czy otrzymane punkty krytyczne spełniają założenie.

Zwróćmy także uwagę na fakt, że często pod pojęciem funkcja uwikłana kryje się więcej niż jedna funkcja, co prowadzi do nieporozumień w sprawie ekstremów. W najprostszym przykładzie, jeśli $F(x,y)=x^2+y^2-1$, to równanie $F(x,y(x))=0$ spełniają dwie funkcje $f_1(x)=\sqrt{1-x^2}$ i $f_2(x)=-\sqrt{1-x^2}$ i obie mają dokładnie jedno ekstremum w tym samym punkcie $x=0$, mianowicie $f_1$ ma maksimum $f_1(0)=1$, a $f_2$ ma minimum $f_2(0)=-1$. Czasami szukając ekstrema funkcji uwikłanej, nie precyzuje się tego, że tam tych funkcji może być więcej i np. w tym prostym przykładzie pisze się, że funkcja uwikłana $y$ ma w $0$ maksimum równe $1$ i ma w $0$ minimum równe $-1$. Trzeba zdawać sobie sprawę, że chodzi tu o dwie funkcje.

Rozwiązanie

a) Rozważamy leminiskatę Bernoullego $F(x,y)=(x^2+y^2{)}^2-2a^2(x^2-y^2)=0$. Obliczmy pochodne cząstkowe

$\begin{array}{rl}& \frac{\partial F}{\partial x}=4x(x^2+y^2)-4x{a}^2=4x(x^2+y^2-a^2),\\ & \frac{\partial F}{\partial y}=4y(x^2+y^2)+4y{a}^2=4y(x^2+y^2+a^2).\\ \end{array}$

Rozwiązujemy układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=4x(x^2+y^2-a^2)=0\\ & F(x,y)=(x^2+y^2{)}^2-2a^2(x^2-y^2)=0.\\ \end{array}$

Z pierwszego równania wynika, że $x=0$ lub $x^2+y^2=a^2$. Podstawiając to wyrażenie do drugiego równania, dostajemy $y=0$ lub $x^2-y^2=\frac{a^2}{2}$. Punkt $(0,0)$ odrzucamy, gdyż w nim $\frac{\partial F}{\partial y}(0,0)=0$. Rozwiązując układ równań

$\{\begin{array}{ll}& x^2+y^2=a^2\\ & x^2-y^2=\frac{a^2}{2},\\ \end{array}$

dostajemy punkty $P_1=(\frac{\sqrt{3}}{2}a,\frac{a}{2})$, $P_2=(-\frac{\sqrt{3}}{2}a,\frac{a}{2})$, $P_3=(\frac{\sqrt{3}}{2}a,-\frac{a}{2})$ i $P_4=(-\frac{\sqrt{3}}{2}a,-\frac{a}{2})$.

Obliczmy drugą pochodną funkcji $y=y(x)$ w jej punktach krytycznych. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=4(x^2+y^2)+8x^2-4a^2,\frac{{\partial }^{2}F}{\partial x^2}(P_i)=8{(\pm \frac{\sqrt{3}}{2}a)}^2=6a^2>0,i=1,2,3,4,\\ & y^{″}(x)=-\frac{\frac{{\partial }^{2}F}{\partial x^2}}{\frac{\partial F}{\partial y}},\mathrm{g}\mathrm{d}\mathrm{y}{y}^{\prime }(x)=0.\end{array}$

W punktach $P_1$ i $P_2$ pochodna cząstkowa $\frac{\partial F}{\partial y}$ jest dodatnia i wtedy $y^{″}<0$. W konsekwencji, jeśli $y\left(\frac{\sqrt{3}}{2}a\right)=\frac{1}{2}a$, to $y$ ma w punkcie $\frac{\sqrt{3}}{2}a$ maksimum o wartości $\frac{1}{2}a$ oraz jeśli $y(-\frac{\sqrt{3}}{2}a)=\frac{1}{2}a$, to $y$ ma również w punkcie $-\frac{\sqrt{3}}{2}a$ maksimum o wartości $\frac{1}{2}a$. Natomiast w punktach $P_3$ i $P_4$ pochodna cząstkowa $\frac{\partial F}{\partial y}$ jest ujemna i wtedy $y^{″}>0$. Zatem jeśli $y\left(\frac{\sqrt{3}}{2}a\right)=-\frac{1}{2}a$, to $y$ ma w punkcie $\frac{\sqrt{3}}{2}a$ minimum o wartości $-\frac{1}{2}a$ oraz jeśli $y(-\frac{\sqrt{3}}{2}a)=-\frac{1}{2}a$, to $y$ ma również w punkcie $-\frac{\sqrt{3}}{2}a$ minimum o wartości $-\frac{1}{2}a$.

b) Rozważamy liść Kartezjusza $F(x,y)=x^3+y^3-3axy=0$. Obliczmy pochodne cząstkowe

$\begin{array}{rl}& \frac{\partial F}{\partial x}=3x^2-3ay,\\ & \frac{\partial F}{\partial y}=3y^2-3ax.\\ \end{array}$

Rozwiązujemy układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=3x^2-3ay=0\\ & F(x,y)=x^3+y^3-3axy=0.\\ \end{array}$

Z pierwszego równania wynika, że $y=\frac{x^2}{a}$. Podstawiając to wyrażenie do drugiego równania, dostajemy $\frac{x^6}{a^3}-2x^3=0$, czyli $x=0$ lub $x=\sqrt[3]{2}a$. Jeżeli $x=0$, to $y=0$. Punkt $(0,0)$ odrzucamy, gdyż $\frac{\partial F}{\partial y}(0,0)=0$. Dostajemy tylko jeden punkt $P=(\sqrt[3]{2}a,\sqrt[3]{4}a)$.

Obliczmy drugą pochodną funkcji $y=y(x)$ w jej punkcie krytycznym. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=6x,\frac{{\partial }^{2}F}{\partial x^2}(\sqrt[3]{2}a,\sqrt[3]{4}a)>0\\ & y^{″}(x)=-\frac{\frac{{\partial }^{2}F}{\partial x^2}}{\frac{\partial F}{\partial y}},\mathrm{g}\mathrm{d}\mathrm{y}{y}^{\prime }(x)=0.\end{array}$

Stąd wynika, że $y^{″}(\sqrt[3]{2}a)<0$, czyli w punkcie $\sqrt[3]{2}a$ funkcja $y$ ma maksimum $y(\sqrt[3]{2}a)=\sqrt[3]{4}a$.

c) Rozważamy równanie $F(x,y,z)=x^2+y^2+z^2-6z=0$. Obliczmy pochodne cząstkowe

$\begin{array}{rlrlr}& \frac{\partial F}{\partial x}=2x,& \frac{\partial F}{\partial y}=2y,& & \frac{\partial F}{\partial z}=2z-6.\end{array}$

Rozwiązujemy układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=2x=0\\ & \frac{\partial F}{\partial y}=2y=0\\ & F(x,y,z)=x^2+y^2+z^2-6z=0.\\ \end{array}$

Z pierwszego równania wynika, że $x=0$, z drugiego, że $y=0$. Podstawiając te równości do trzeciego równania, dostajemy $z^2-6z=0$, czyli otrzymujemy punkty $P_1=(0,0,0)$ i $P_2=(0,0,6)$.

Obliczmy pochodne cząstkowe rzędu drugiego $z=z(x,y)$ w jej punktach krytycznych. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=2,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=0,\\ & \frac{{\partial }^{2}F}{\partial y^2}=2,\\ & \frac{{\partial }^{2}z}{\partial x^2}=-\frac{\frac{{\partial }^{2}F}{\partial x^2}}{\frac{\partial F}{\partial z}}=-\frac{2}{2z-6},\\ & \frac{{\partial }^{2}z}{\partial x\partial y}=-\frac{\frac{{\partial }^{2}F}{\partial x\partial y}}{\frac{\partial F}{\partial z}}=0,\\ & \frac{{\partial }^{2}z}{\partial y^2}=-\frac{\frac{{\partial }^{2}F}{\partial y^2}}{\frac{\partial F}{\partial z}}=-\frac{2}{2z-6},\\ \end{array}$

przy czym ostatnie trzy równości zachodzą oczywiście w punktach zerowania się pierwszej różniczki funkcji $z$.

Jeśli $z(0,0)=0$, to macierz drugiej różniczki $d_{(0,0)}^{2}z$ ma postać

$\left[\begin{array}{cc}\frac{1}{3}& 0\\ 0& \frac{1}{3}\end{array}\right]$

jest więc dodatnio określona, czyli funkcja $z$ ma minimum $z(0,0)=0$.

Jeśli $z(0,0)=6$, to macierz drugiej różniczki $d_{(0,0)}^{2}z$ ma postać

$\left[\begin{array}{cc}-\frac{1}{3}& 0\\ 0& -\frac{1}{3}\end{array}\right]$

jest więc ujemnie określona, czyli funkcja $z$ ma maksimum $z(0,0)=6$.

d) Rozważamy równanie $F(x,y,z)=x-z\ln (\frac{z}{y})=0$. Obliczmy pochodne cząstkowe

$\begin{array}{rl}& \frac{\partial F}{\partial x}=1,\\ & \frac{\partial F}{\partial y}=\frac{z}{y},\\ & \frac{\partial F}{\partial z}=-1-\ln \frac{z}{y}.\\ \end{array}$

Z warunku koniecznego $z$ nie ma żadnego ekstremum, gdyż pochodna cząstkowa po $x$ jest niezerowa.

e) Rozważamy równanie $F(x,y,z)=z^3-3xyz-20=0$. Obliczmy pochodne cząstkowe

$\begin{array}{rl}& \frac{\partial F}{\partial x}=-3yz,\\ & \frac{\partial F}{\partial y}=-3xz,\\ & \frac{\partial F}{\partial z}=3z^2-3xy.\\ \end{array}$

Rozwiązujemy układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=-3yz=0\\ & \frac{\partial F}{\partial y}=-3xz=0\\ & F(x,y,z)=z^3-3xyz-20=0.\\ \end{array}$

Zauważmy, że $z\ne 0$ wobec trzeciego równania, czyli rozwiązaniem układu jest $P=(0,0,\sqrt[3]{20})$. Obliczmy pochodne cząstkowe rzędu drugiego funkcji $z=z(x,y)$ w jej punkcie krytycznym. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=0,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=-3z,\\ & \frac{{\partial }^{2}F}{\partial y^2}=0,\\ & \frac{{\partial }^{2}z}{\partial x^2}=-\frac{\frac{{\partial }^{2}F}{\partial x^2}}{\frac{\partial F}{\partial z}}=0,\\ & \frac{{\partial }^{2}z}{\partial x\partial y}=-\frac{\frac{{\partial }^{2}F}{\partial x\partial y}}{\frac{\partial F}{\partial z}}=-\frac{-3z}{3z^2-3xy},\\ & \frac{{\partial }^{2}z}{\partial y^2}=-\frac{\frac{{\partial }^{2}F}{\partial y^2}}{\frac{\partial F}{\partial z}}=0,\\ \end{array}$

przy czym ostatnie trzy równości zachodzą oczywiście w punktach zerowania się pierwszej różniczki funkcji $z$.

W punkcie $(0,0)$ macierz drugiej różniczki $d_{(0,0)}^{2}z$ ma postać

$\left[\begin{array}{cc}0& \frac{1}{\sqrt[3]{2}0}\\ \frac{1}{\sqrt[3]{2}0}& 0\end{array}\right]$

jest więc nieokreślona, czyli funkcja $z$ nie ma w tym punkcie ekstremum.

Ćwiczenie 9.7.

Znaleźć ekstrema warunkowe funkcji

a) $f(x,y)=x^2+y^2$ pod warunkiem $g(x,y)=x^3+y^3-16=0$,

b) $f(x,y)=\frac{1}{x^2}+\frac{1}{y^2}$ pod warunkiem $g(x,y)=x+y-3=0$,

c) $f(x,y)=2x^2{y}^2$ pod warunkiem $g(x,y)=x^4+y^4-1=0$,

d) $f(x,y)=x^4+y^4$ pod warunkiem $g(x,y)=x^2{y}^2-1=0$.

Wskazówka

Wykorzystać metodę mnożników Lagrange'a. Określoność formy kwadratowej

$h\mapsto (d_a^{2}f-\lambda d_a^{2}g)(h,h)$

wystarczy badać na podprzestrzeni $X_1=\{h\in {\mathbb{ℝ}}^2:d_{a}g(h)=0\}$.

c) Rozwiązując układ równań, rozważyć najpierw przypadek $x=0$, później $y=0$, wreszcie jeśli $x\ne 0$ i $y\ne 0$, wyliczyć $\lambda$ (wstawiając odpowiednio z pierwszego równania do drugiego $y^2$) i wstawić do pierwszego równania, uzyskując zależność między $x$ i $y$.

d) Rozwiązując układ równań, zauważyć, że dla punktów spełniających go, $x\ne 0$, $y\ne 0$ i $\lambda >0$ i skorzystać ze wskazówki do punktu c).

Rozwiązanie

a) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$F(x,y,\lambda )=f(x,y)-\lambda g(x,y)=x^2+y^2-\lambda (x^3+y^3-16)$

Rozwiązując układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=2x-3\lambda x^2=0\\ & \frac{\partial F}{\partial y}=2y-3\lambda y^2=0\\ & \frac{\partial F}{\partial \lambda }=-(x^3+y^3-16)=0,\\ \end{array}$

otrzymujemy punkty $P_1=(0,2\sqrt[3]{2})$ ($\lambda =\frac{1}{3\sqrt[3]{2}}$), $P_2=(2\sqrt[3]{2},0)$ ($\lambda =\frac{1}{3\sqrt[3]{2}}$) i $P_3=(2,2)$ ($\lambda =\frac{1}{3}$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$ w punktach krytycznych. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=2-6\lambda x,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=0,\\ & \frac{{\partial }^{2}F}{\partial y^2}=2-6\lambda y.\\ \end{array}$

W punkcie $P_1=(0,2\sqrt[3]{2})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}2& 0\\ 0& -2\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_1)+B\frac{\partial g}{\partial y}(P_1)=0\cdot A+12\sqrt[3]{4}B$,

a stąd $B=0$, $A$-dowolne. Mamy

$\left[\begin{array}{cc}A& 0\end{array}\right]\left[\begin{array}{cc}2& 0\\ 0& -2\end{array}\right]\left[\begin{array}{c}A\\ 0\end{array}\right]=2A^2>0,\mathrm{d}\mathrm{l}\mathrm{a}A\ne 0$,

czyli macierz jest dodatnio określona na wektorach postaci $(A,0)$. Dlatego funkcja $f$ ma w punkcie $P_1$ minimum warunkowe równe $f(P_1)=4\sqrt[3]{4}$.

W punkcie $P_2=(2\sqrt[3]{2},0)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}-2& 0\\ 0& 2\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_2)+B\frac{\partial g}{\partial y}(P_2)=12\sqrt[3]{4}A+0\cdot B$,

a stąd $A=0$, $B$-dowolne. Mamy

$\left[\begin{array}{cc}0& B\end{array}\right]\left[\begin{array}{cc}-2& 0\\ 0& 2\end{array}\right]\left[\begin{array}{c}0\\ B\end{array}\right]=2B^2>0,\mathrm{d}\mathrm{l}\mathrm{a}B\ne 0$,

czyli macierz jest dodatnio określona na wektorach postaci $(0,B)$. Dlatego funkcja $f$ ma w punkcie $P_2$ minimum warunkowe równe $f(P_2)=4\sqrt[3]{4}$.

W punkcie $P_3=(2,2)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}-2& 0\\ 0& -2\end{array}\right]$

jest więc ujemnie określona, czyli funkcja $f$ ma w punkcie $P_3$ maksimum warunkowe równe $f(P_3)=8$.

b) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$F(x,y,\lambda )=f(x,y)-\lambda g(x,y)=\frac{1}{x^2}+\frac{1}{y^2}-\lambda (x+y-3)$

Rozwiązaniem układu równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=-\frac{2}{x^3}-\lambda =0\\ & \frac{\partial F}{\partial y}=-\frac{2}{y^3}-\lambda =0\\ & \frac{\partial F}{\partial \lambda }=-(x+y-3)=0\\ \end{array}$

jest punkt $P=(\frac{3}{2},\frac{3}{2})$ ($\lambda =-\frac{16}{27}$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=\frac{6}{x^4},\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=0,\\ & \frac{{\partial }^{2}F}{\partial y^2}=\frac{6}{y^4}.\\ \end{array}$

W punkcie $P=(\frac{3}{2},\frac{3}{2})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}\frac{96}{81}& 0\\ 0& \frac{96}{81}\end{array}\right]$

jest więc dodatnio określona, czyli funkcja $f$ ma w punkcie $P$ minimum warunkowe równe $f(P)=\frac{8}{9}$.

c) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$F(x,y,\lambda )=f(x,y)-\lambda g(x,y)=2x^2{y}^2-\lambda (x^4+y^4-1)$

Rozwiązując układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=4x{y}^2-4\lambda x^3=0\\ & \frac{\partial F}{\partial y}=4y{x}^2-4\lambda y^3=0\\ & \frac{\partial F}{\partial \lambda }=-(x^4+y^4-1)=0,\\ \end{array}$

otrzymujemy punkty $P_1=(0,1)$ ($\lambda =0$), $P_2=(0,-1)$ ($\lambda =0$), $P_3=(1,0)$ ($\lambda =0$), $P_4=(-1,0)$ ($\lambda =0$), $P_5=(\sqrt[4]{\frac{1}{2}},\sqrt[4]{\frac{1}{2}})$ ($\lambda =1$), $P_6=(-\sqrt[4]{\frac{1}{2}},-\sqrt[4]{\frac{1}{2}})$ ($\lambda =1$), $P_7=(-\sqrt[4]{\frac{1}{2}},\sqrt[4]{\frac{1}{2}})$ ($\lambda =1$), $P_8=(\sqrt[4]{\frac{1}{2}},-\sqrt[4]{\frac{1}{2}})$ ($\lambda =1$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=4y^2-12\lambda x^2,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=8xy,\\ & \frac{{\partial }^{2}F}{\partial y^2}=4x^2-12\lambda y^2.\\ \end{array}$

W punkcie $P_1=(0,1)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}4& 0\\ 0& 0\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_1)+B\frac{\partial g}{\partial y}(P_1)=0\cdot A+4B$,

a stąd $B=0$, $A$-dowolne. Mamy

$\left[\begin{array}{cc}A& 0\end{array}\right]\left[\begin{array}{cc}4& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}A\\ 0\end{array}\right]=4A^2>0,\mathrm{d}\mathrm{l}\mathrm{a}A\ne 0$,

czyli macierz jest dodatnio określona na wektorach postaci $(A,0)$. Dlatego funkcja $f$ ma w punkcie $P_1$ minimum warunkowe równe $f(P_1)=0$. Analogicznie badamy punkt $P_2=(0,-1)$ i stwierdzamy, że funkcja $f$ ma w punkcie $P_2$ minimum warunkowe równe $f(P_2)=0$.

W punkcie $P_3=(1,0)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}0& 0\\ 0& 4\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_3)+B\frac{\partial g}{\partial y}(P_3)=4A+0\cdot B$,

a stąd $A=0$, $B$-dowolne. Mamy

$\left[\begin{array}{cc}0& B\end{array}\right]\left[\begin{array}{cc}0& 0\\ 0& 4\end{array}\right]\left[\begin{array}{c}0\\ B\end{array}\right]=4B^2>0,\mathrm{d}\mathrm{l}\mathrm{a}B\ne 0$,

czyli macierz jest dodatnio określona na wektorach postaci $(0,B)$. Dlatego funkcja $f$ ma w punkcie $P_3$ minimum warunkowe równe $f(P_3)=0$. Analogicznie badamy punkt $P_4=(-1,0)$ i stwierdzamy, że funkcja $f$ ma w punkcie $P_4$ minimum warunkowe równe $f(P_4)=0$.

W punkcie $P_5=(\sqrt[4]{\frac{1}{2}},\sqrt[4]{\frac{1}{2}})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}-8\sqrt{\frac{1}{2}}& 8\sqrt{\frac{1}{2}}\\ 8\sqrt{\frac{1}{2}}& -8\sqrt{\frac{1}{2}}\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_5)+B\frac{\partial g}{\partial y}(P_5)=4{\left(\frac{1}{2}\right)}^{\frac{3}{4}}(A+B)=0$,

a stąd $A=-B$. Mamy

$\left[\begin{array}{cc}A& -A\end{array}\right]\left[\begin{array}{cc}-8\sqrt{\frac{1}{2}}& 8\sqrt{\frac{1}{2}}\\ 8\sqrt{\frac{1}{2}}& -8\sqrt{\frac{1}{2}}\end{array}\right]\left[\begin{array}{c}A\\ -A\end{array}\right]=-32\sqrt{\frac{1}{2}}{A}^2<0,\mathrm{d}\mathrm{l}\mathrm{a}A\ne 0$,

czyli macierz jest ujemnie określona na wektorach postaci $(A,-A)$. Dlatego funkcja $f$ ma w punkcie $P_5$ maksimum warunkowe równe $f(P_5)=1$. Analogicznie badamy punkt $P_6=(-\sqrt[4]{\frac{1}{2}},-\sqrt[4]{\frac{1}{2}})$ i stwierdzamy, że funkcja $f$ ma w punkcie $P_6$ maksimum warunkowe równe $f(P_6)=1$.

W punkcie $P_7=(-\sqrt[4]{\frac{1}{2}},\sqrt[4]{\frac{1}{2}})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}-8\sqrt{\frac{1}{2}}& -8\sqrt{\frac{1}{2}}\\ -8\sqrt{\frac{1}{2}}& -8\sqrt{\frac{1}{2}}\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_5)+B\frac{\partial g}{\partial y}(P_5)=4{\left(\frac{1}{2}\right)}^{\frac{3}{4}}(-A+B)=0$,

a stąd $A=B$. Mamy

$\left[\begin{array}{cc}A& A\end{array}\right]\left[\begin{array}{cc}-8\sqrt{\frac{1}{2}}& -8\sqrt{\frac{1}{2}}\\ -8\sqrt{\frac{1}{2}}& -8\sqrt{\frac{1}{2}}\end{array}\right]\left[\begin{array}{c}A\\ A\end{array}\right]=-32\sqrt{\frac{1}{2}}{A}^2<0,\mathrm{d}\mathrm{l}\mathrm{a}A\ne 0$,

czyli macierz jest ujemnie określona na wektorach postaci $(A,A)$. Dlatego funkcja $f$ ma w punkcie $P_7$ maksimum warunkowe równe $f(P_7)=1$. Analogicznie badamy punkt $P_8=(\sqrt[4]{\frac{1}{2}},-\sqrt[4]{\frac{1}{2}})$ i stwierdzamy, że funkcja $f$ ma w punkcie $P_8$ maksimum warunkowe równe $f(P_8)=1$.

d) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$F(x,y,\lambda )=f(x,y)-\lambda g(x,y)=x^4+y^4-\lambda (x^2{y}^2-1)$

Rozwiązując układu równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=4x^3-2\lambda x{y}^2=0\\ & \frac{\partial F}{\partial y}=4y^3-2\lambda x^{2}y=0\\ & \frac{\partial F}{\partial \lambda }=-(x^2{y}^2-1)=0,\\ \end{array}$

otrzymujemy punkty $P_1=(1,1)$ ($\lambda =2$), $P_2=(-1,-1)$ ($\lambda =2$), $P_3=(1,-1)$ ($\lambda =2$) i $P_4=(-1,1)$ ($\lambda =2$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=12x^2-2\lambda y^2,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=-4\lambda xy,\\ & \frac{{\partial }^{2}F}{\partial y^2}=12y^2-2\lambda x^2.\\ \end{array}$

W punkcie $P_1=(1,1)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}8& -8\\ -8& 8\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_1)+B\frac{\partial g}{\partial y}(P_1)=2A+2B$,

a stąd $A=-B$. Mamy

$\left[\begin{array}{cc}A& -A\end{array}\right]\left[\begin{array}{cc}8& -8\\ -8& 8\end{array}\right]\left[\begin{array}{c}A\\ -A\end{array}\right]=32A^2>0,\mathrm{d}\mathrm{l}\mathrm{a}A\ne 0$,

czyli macierz jest dodatnio określona na wektorach postaci $(A,-A)$. Dlatego funkcja $f$ ma w punkcie $P_1$ minimum warunkowe równe $f(P_1)=2$. Analogicznie badamy punkt $P_2=(-1,-1)$ i stwierdzamy, że funkcja $f$ ma w punkcie $P_2$ minimum warunkowe równe $f(P_2)=2$.

W punkcie $P_3=(1,-1)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{cc}8& 8\\ 8& 8\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_3)+B\frac{\partial g}{\partial y}(P_3)=2A-2B$,

a stąd $A=B$. Mamy

$\left[\begin{array}{cc}A& A\end{array}\right]\left[\begin{array}{cc}8& 8\\ 8& 8\end{array}\right]\left[\begin{array}{c}A\\ A\end{array}\right]=32A^2>0,\mathrm{d}\mathrm{l}\mathrm{a}A\ne 0$,

czyli macierz jest dodatnio określona na wektorach postaci $(A,A)$. Dlatego funkcja $f$ ma w punkcie $P_3$ minimum warunkowe równe $f(P_3)=2$. Analogicznie badamy punkt $P_4=(-1,1)$ i stwierdzamy, że funkcja $f$ ma w punkcie $P_4$ minimum warunkowe równe $f(P_4)=2$.

Ćwiczenie 9.8.

Znaleźć ekstrema warunkowe funkcji

a) $f(x,y,z)=x^2+y^2+z^2$ pod warunkiem $g(x,y)=x+y+z-1=0$,

b) $f(x,y,z)=x+y+z$ pod warunkiem $g(x,y)=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-1=0$,

c) $f(x,y,z)=xyz$ pod warunkiem $g(x,y)=x+y+z-1=0$.

Wskazówka

Wykorzystać metodę mnożników Lagrange'a. Określoność formy kwadratowej

$h\mapsto (d_a^{2}f-\lambda d_a^{2}g)(h,h)$

wystarczy badać na podprzestrzeni $X_1=\{h\in {\mathbb{ℝ}}^3:d_{a}g(h)=0\}$.

Rozwiązanie

a) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$F(x,y,z,\lambda )=f(x,y,z)-\lambda g(x,y,z)=x^2+y^2+z^2-\lambda (x+y+z-1)$

Punkty krytyczne dostajemy rozwiązując układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=2x-\lambda =0\\ & \frac{\partial F}{\partial y}=2y-\lambda =0\\ & \frac{\partial F}{\partial z}=2z-\lambda =0\\ & \frac{\partial F}{\partial \lambda }=-(x+y+z-1)=0.\\ \end{array}$

Rozwiązaniem tego układu równań jest punkt $P=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ ($\lambda =\frac{2}{3}$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=\frac{{\partial }^{2}F}{\partial y^2}=\frac{{\partial }^{2}F}{\partial z^2}=2,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=\frac{{\partial }^{2}F}{\partial x\partial z}=\frac{{\partial }^{2}F}{\partial z\partial y}=0.\\ \end{array}$

W punkcie $P=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 2\end{array}\right]$

jest więc dodatnio określona, czyli funkcja $f$ ma w punkcie $P$ minimum warunkowe równe $f(P)=\frac{1}{3}$.

b) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$F(x,y,z,\lambda )=f(x,y,z)-\lambda g(x,y,z)=x+y+z-\lambda (\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-1)$

Rozwiązując układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=1+\frac{\lambda }{x^2}=0\\ & \frac{\partial F}{\partial y}=1+\frac{\lambda }{y^2}=0\\ & \frac{\partial F}{\partial z}=1+\frac{\lambda }{z^2}=0\\ & \frac{\partial F}{\partial \lambda }=-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-1)=0,\\ \end{array}$

otrzymujemy punkty $P_1=(3,3,3)$ ($\lambda =-9$), $P_2=(1,1,-1)$ ($\lambda =-1$), $P_3=(1,-1,1)$ ($\lambda =-1$) i $P_4=(-1,1,1)$ ($\lambda =-1$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=-\frac{2\lambda }{x^3},\\ & \frac{{\partial }^{2}F}{\partial y^2}=-\frac{2\lambda }{y^3},\\ & \frac{{\partial }^{2}F}{\partial z^2}=-\frac{2\lambda }{z^3},\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=\frac{{\partial }^{2}F}{\partial x\partial z}=\frac{{\partial }^{2}F}{\partial z\partial y}=0.\\ \end{array}$

W punkcie $P_1=(3,3,3)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}\frac{2}{3}& 0& 0\\ 0& \frac{2}{3}& 0\\ 0& 0& \frac{2}{3}\end{array}\right]$,

jest więc dodatnio określona, czyli funkcja $f$ ma w punkcie $P$ minimum warunkowe równe $f(P_1)=9$.

W punkcie $P_2=(1,1,-1)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& -2\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B,C)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_2)+B\frac{\partial g}{\partial y}(P_2)+C\frac{\partial g}{\partial z}(P_2)=-A-B-C$,

a stąd $C=-A-B$. Mamy

$\left[\begin{array}{ccc}A& B& -A-B\end{array}\right]\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& -2\end{array}\right]\left[\begin{array}{c}A\\ B\\ -A-B\end{array}\right]=-4AB$,

czyli macierz jest nieokreślona. Dlatego funkcja $f$ nie ma w punkcie $P_2$ ekstremum. Podobnie badamy punkty $P_3$ i $P_4$ i stwierdzamy, że funkcja $f$ nie ma ekstremów w tych punktach.

c) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$F(x,y,z,\lambda )=f(x,y,z)-\lambda g(x,y,z)=xyz-\lambda (x+y+z-1)$

Rozwiązując układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=yz-\lambda =0\\ & \frac{\partial F}{\partial y}=xz-\lambda =0\\ & \frac{\partial F}{\partial z}=xy-\lambda =0\\ & \frac{\partial F}{\partial \lambda }=-(x+y+z-1)=0,\\ \end{array}$

otrzymujemy punkty $P_1=(0,0,1)$ ($\lambda =0$), $P_2=(0,1,0)$ ($\lambda =0$), $P_3=(1,0,0)$ ($\lambda =0$) i $P_4=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ ($\lambda =\frac{1}{9}$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=\frac{{\partial }^{2}F}{\partial y^2}=\frac{{\partial }^{2}F}{\partial z^2}=0,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=z,\\ & \frac{{\partial }^{2}F}{\partial x\partial z}=y,\\ & \frac{{\partial }^{2}F}{\partial z\partial y}=x.\\ \end{array}$

W punkcie $P_1=(0,0,1)$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B,C)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_2)+B\frac{\partial g}{\partial y}(P_2)+C\frac{\partial g}{\partial z}(P_2)=A+B+C$,

a stąd $C=-A-B$. Mamy

$\left[\begin{array}{ccc}A& B& -A-B\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}A\\ B\\ -A-B\end{array}\right]=2AB$,

czyli macierz jest nieokreślona. Dlatego funkcja $f$ nie ma w punkcie $P_1$ ekstremum. Podobnie badamy punkty $P_2$ i $P_3$ i stwierdzamy, że funkcja $f$ nie ma ekstremów w tych punktach.

W punkcie $P_4=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}0& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& 0& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& 0\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B,C)$ spełniających warunek

$0=A\frac{\partial g}{\partial x}(P_2)+B\frac{\partial g}{\partial y}(P_2)+C\frac{\partial g}{\partial z}(P_2)=A+B+C$,

a stąd $C=-A-B$.Mamy

$\left[\begin{array}{ccc}A& B& -A-B\end{array}\right]\left[\begin{array}{ccc}0& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& 0& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& 0\end{array}\right]\left[\begin{array}{c}A\\ B\\ -A-B\end{array}\right]=-\frac{1}{3}{A}^2-\frac{1}{3}{B}^2-\frac{1}{3}(A+B{)}^2<0,\mathrm{g}\mathrm{d}\mathrm{y}A\ne 0\mathrm{l}\mathrm{u}\mathrm{b}B\ne 0$,

czyli macierz jest ujemnie określona. Dlatego funkcja $f$ ma w punkcie $P_4$ maksimum warunkowe równe $f(P_4)=\frac{1}{27}$.

Ćwiczenie 9.9.

Znaleźć ekstrema warunkowe funkcji

a) $f(x,y,z)=x+y+z$ pod warunkami $g(x,y,z)=x^2+y^2-1=0$ i $h(x,y,z)=x^2+z^2-1=0$,

b) $f(x,y,z)=xyz$ pod warunkami $g(x,y,z)=x^2+y^2+z^2-1=0$ i $h(x,y,z)=x+y+z=0$.

Wskazówka

Wykorzystać metodę mnożników Lagrange'a. Określoność formy kwadratowej

$h\mapsto (d_a^{2}f-\lambda d_a^2(g,h))(k,k)$

wystarczy badać na podprzestrzeni $X_1=\{k\in {\mathbb{ℝ}}^3:d_a(g,h)(k)=(0,0)\}$.

b) Rozwiązując układ równań, odjąć stronami pierwsze dwa równania, pogrupować wyrazy podobne i przedstawić w postaci iloczynu dwóch czynników, który równa się zero.

Rozwiązanie

a) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$\begin{array}{lll}F(x,y,z,\lambda ,\mu )& =& f(x,y,z)-\lambda g(x,y,z)-\mu h(x,y,z)\\ & =& x+y+z-\lambda (x^2+y^2-1)-\mu (x^2+z^2-1).\end{array}$

Rozwiązując układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=1-2\lambda x-2\mu x=0\\ & \frac{\partial F}{\partial y}=1-2\lambda y=0\\ & \frac{\partial F}{\partial z}=1-2\mu z=0\\ & \frac{\partial F}{\partial \lambda }=-(x^2+y^2-1)=0\\ & \frac{\partial F}{\partial \mu }=-(x^2+z^2-1)=0,\\ \end{array}$

otrzymujemy punkty $P_1=(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}},\frac{2}{\sqrt{5}})$ ($\lambda =\mu =\frac{\sqrt{5}}{4}$) i $P_2=(-\frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}},-\frac{2}{\sqrt{5}})$ ($\lambda =\mu =-\frac{\sqrt{5}}{4}$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=-2\lambda -2\mu \\ & \frac{{\partial }^{2}F}{\partial y^2}=-2\lambda \\ & \frac{{\partial }^{2}F}{\partial z^2}=-2\mu ,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=\frac{{\partial }^{2}F}{\partial x\partial z}=\frac{{\partial }^{2}F}{\partial z\partial y}=0.\\ \end{array}$

W punkcie $P_1=(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}},\frac{2}{\sqrt{5}})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}-\sqrt{5}& 0& 0\\ 0& -\frac{\sqrt{5}}{2}& 0\\ 0& 0& -\frac{\sqrt{5}}{2}\end{array}\right]$,

jest więc ujemnie określona, czyli funkcja $f$ ma w punkcie $P_1$ maksimum warunkowe równe $f(P_1)=\sqrt{5}$.

W punkcie $P_2=(-\frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}},-\frac{2}{\sqrt{5}})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}\sqrt{5}& 0& 0\\ 0& \frac{\sqrt{5}}{2}& 0\\ 0& 0& \frac{\sqrt{5}}{2}\end{array}\right]$,

jest więc dodatnio określona, czyli funkcja $f$ ma w punkcie $P_2$ minimum warunkowe równe $f(P_2)=-\sqrt{5}$.

b) Stosujemy metodę mnożników Lagrange'a. Tworzymy nową funkcję

$\begin{array}{lll}F(x,y,z,\lambda ,\mu )& =& f(x,y,z)-\lambda g(x,y,z)-\mu h(x,y,z)\\ & =& xyz-\lambda (x^2+y^2+z^2-1)-\mu (x+y+z).\end{array}$

Rozwiązując układ równań

$\{\begin{array}{ll}& \frac{\partial F}{\partial x}=yz-2\lambda x-\mu =0\\ & \frac{\partial F}{\partial y}=xz-2\lambda y-\mu =0\\ & \frac{\partial F}{\partial z}=xy-2\lambda z-\mu =0\\ & \frac{\partial F}{\partial \lambda }=-(x^2+y^2+z^2-1)=0\\ & \frac{\partial F}{\partial \mu }=-(x+y+z)=0,\\ \end{array}$

otrzymujemy punkty $P_1=(-\frac{1}{\sqrt{6}},\frac{2}{\sqrt{6}},-\frac{1}{\sqrt{6}})$ ($\lambda =\frac{1}{2\sqrt{6}},\mu =-\frac{1}{6}$), $P_2=(\frac{2}{\sqrt{6}},-\frac{1}{\sqrt{6}},-\frac{1}{\sqrt{6}})$ ($\lambda =\frac{1}{2\sqrt{6}},\mu =-\frac{1}{6}$), $P_3=(-\frac{1}{\sqrt{6}},-\frac{1}{\sqrt{6}},\frac{2}{\sqrt{6}})$ ($\lambda =\frac{1}{2\sqrt{6}},\mu =-\frac{1}{6}$), $P_4=(\frac{1}{\sqrt{6}},-\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}})$ ($\lambda =-\frac{1}{2\sqrt{6}},\mu =-\frac{1}{6}$), $P_5=(-\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}})$ ($\lambda =-\frac{1}{2\sqrt{6}},\mu =-\frac{1}{6}$), $P_6=(\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}},-\frac{2}{\sqrt{6}})$ ($\lambda =-\frac{1}{2\sqrt{6}},\mu =-\frac{1}{6}$).

Obliczmy pochodne cząstkowe rzędu drugiego funkcji $F$. Mamy

$\begin{array}{rl}& \frac{{\partial }^{2}F}{\partial x^2}=\frac{{\partial }^{2}F}{\partial y^2}=\frac{{\partial }^{2}F}{\partial z^2}=-2\lambda ,\\ & \frac{{\partial }^{2}F}{\partial x\partial y}=z,\\ & \frac{{\partial }^{2}F}{\partial x\partial z}=y,\\ & \frac{{\partial }^{2}F}{\partial z\partial y}=x.\\ \end{array}$

W punkcie $P_1=(-\frac{1}{\sqrt{6}},\frac{2}{\sqrt{6}},-\frac{1}{\sqrt{6}})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}-\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{6}}& \frac{2}{\sqrt{6}}\\ -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{6}}\\ \frac{2}{\sqrt{6}}& -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{6}}\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B,C)$ spełniających warunki

$\begin{array}{rl}& 0=A\frac{\partial g}{\partial x}(P_1)+B\frac{\partial g}{\partial y}(P_1)+C\frac{\partial g}{\partial z}(P_1)=-\frac{2}{\sqrt{6}}A+\frac{4}{\sqrt{6}}B-\frac{2}{\sqrt{6}}C,\\ & 0=A\frac{\partial h}{\partial x}(P_1)+B\frac{\partial h}{\partial y}(P_1)+C\frac{\partial h}{\partial z}(P_1)=A+B+C,\end{array}$

a stąd $C=-A$ i $B=0$. Mamy

$\left[\begin{array}{ccc}A& 0& -A\end{array}\right]\left[\begin{array}{ccc}-\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{6}}& \frac{2}{\sqrt{6}}\\ -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{6}}\\ \frac{2}{\sqrt{6}}& -\frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{6}}\end{array}\right]\left[\begin{array}{c}A\\ 0\\ -A\end{array}\right]=-\sqrt{6}{A}^2<0,\mathrm{g}\mathrm{d}\mathrm{y}A\ne 0$,

czyli macierz jest ujemnie określona. Dlatego funkcja $f$ ma w punkcie $P_1$ maksimum warunkowe równe $f(P_1)=\frac{1}{3\sqrt{6}}$. Podobnie badamy punkty $P_2$ i $P_3$ i stwierdzamy, że funkcja $f$ ma maksimum warunkowe w każdym z tych punktów równe $f(P_2)=f(P_3)=\frac{1}{3\sqrt{6}}$.

W punkcie $P_4=(\frac{1}{\sqrt{6}},-\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}})$ macierz drugiej różniczki ma postać

$\left[\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}& -\frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}\\ -\frac{2}{\sqrt{6}}& \frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}\end{array}\right]$

Badamy określoność tej macierzy dla wektorów $(A,B,C)$ spełniających warunki

$\begin{array}{rl}& 0=A\frac{\partial g}{\partial x}(P_4)+B\frac{\partial g}{\partial y}(P_4)+C\frac{\partial g}{\partial z}(P_4)=\frac{2}{\sqrt{6}}A-\frac{4}{\sqrt{6}}B+\frac{2}{\sqrt{6}}C,\\ & 0=A\frac{\partial h}{\partial x}(P_4)+B\frac{\partial h}{\partial y}(P_4)+C\frac{\partial h}{\partial z}(P_4)=A+B+C,\end{array}$

a stąd $C=-A$ i $B=0$. Mamy

$\left[\begin{array}{ccc}A& 0& -A\end{array}\right]\left[\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}& -\frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}\\ -\frac{2}{\sqrt{6}}& \frac{1}{\sqrt{6}}& \frac{1}{\sqrt{6}}\end{array}\right]\left[\begin{array}{c}A\\ 0\\ -A\end{array}\right]=\sqrt{6}{A}^2>0,\mathrm{g}\mathrm{d}\mathrm{y}A\ne 0$,

czyli macierz jest dodatnio określona. Dlatego funkcja $f$ ma w punkcie $P_4$ minimum warunkowe równe $f(P_4)=-\frac{1}{3\sqrt{6}}$. Podobnie badamy punkty $P_5$ i $P_6$ i stwierdzamy, że funkcja $f$ ma minimum warunkowe w każdym z tych punktów równe $f(P_5)=f(P_6)=-\frac{1}{3\sqrt{6}}$.