Analiza matematyczna 2/Ćwiczenia 6: Ciągłość funkcji wielu zmiennych. Pochodne cząstkowe. Gradient
Funkcje wielu zmiennych. Ciągłość. Pochodne cząstkowe
Ćwiczenie 6.1.
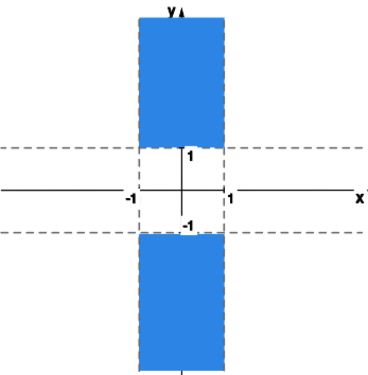
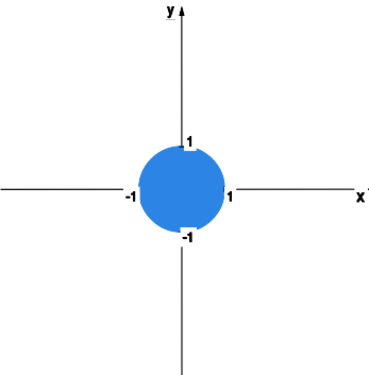
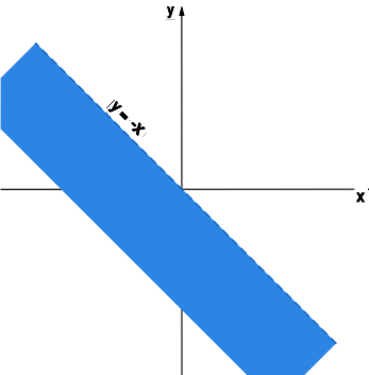
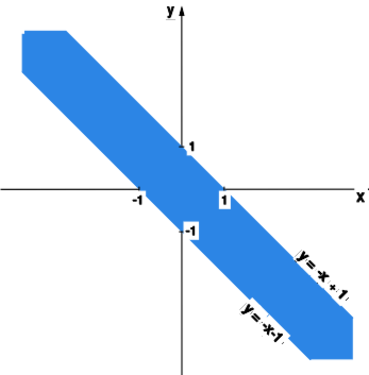
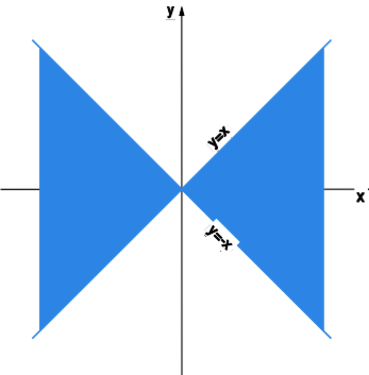
Wyznaczyć dziedzinę funkcji
a) ,
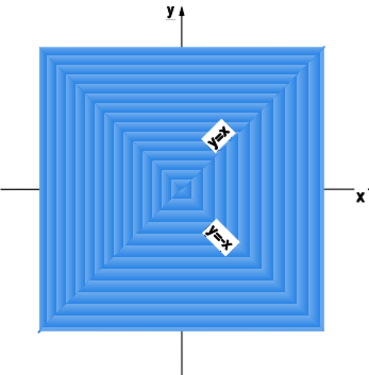
b) ,
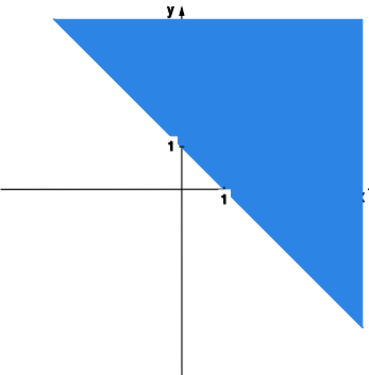
c) ,
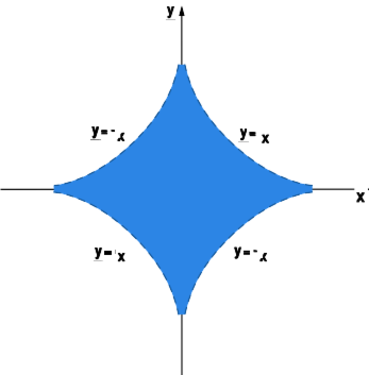
d) ,
e) ,
f) ,
g) ,
h) ,
i) .
Ćwiczenie 6.2.
Obliczyć granice iterowane i granice funkcji (o ile istnieją)
Ćwiczenie 6.3.
Zbadać ciągłość funkcji
Ćwiczenie 6.4.
Obliczyć pochodne cząstkowe rzędu pierwszego następujących funkcji
a) ,
b) ,
c) ,
d) ,
e) ,
f) ,
g) .
Ćwiczenie 6.5.
Udowodnić zależność między pochodną kierunkową a pochodnymi cząstkowymi
,
o ile one wszystkie istnieją i o ile pochodne cząstkowe są ciągłe. Obliczyć pochodne kierunkowe funkcji
w kierunku wektora w punkcie ,
b) w kierunku wektora w punkcie ,
c) w kierunku wektora w punkcie .
Ćwiczenie 6.6.
Obliczyć pochodne cząstkowe rzędu pierwszego następujących funkcji złożonych
a) , gdzie jest funkcją różniczkowalną,
b) , gdzie jest funkcją różniczkowalną,
c) , gdzie jest funkcją różniczkowalną.
Ćwiczenie 6.7.
Sprawdzić, czy funkcja
a) spełnia równanie
b) spełnia równanie
c) , gdzie jest funkcją różniczkowalną, spełnia równanie
d) , gdzie funkcja ma pochodne cząstkowe, spełnia równanie
Ćwiczenie 6.8.
Obliczyć
a) , gdzie ,
b) , gdzie ,
c) , gdzie
Ćwiczenie 6.9.
Dane równanie zapisać w nowych współrzędnych