PEE Zadania z rozwiązaniami
Zadanie 1
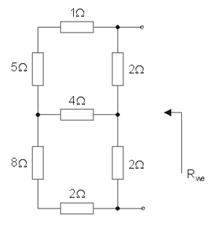
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej:
Rozwiązanie
Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się .
Zadanie 2
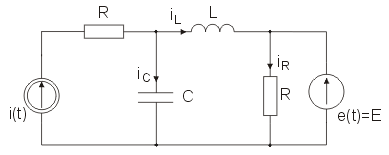
Napisać równanie węzłowe dla obwodu z rysunku poniżej. Potencjały węzłów zaznaczono na rysunku w postaci i . Rozwiązać to równanie wyznaczając potencjały węzłów oraz prądy w gałęziach (prądy rezystancji, pojemności i indukcyjności). Przyjąć: , , , , , ,
Rozwiązanie
Wartości zespolone:
Równanie admitancyjne
Z rozwiązania tego macierzowego układu równań mamy
Prądy w obwodzie:
- (prąd rezystora i źródła )
Zadanie 3
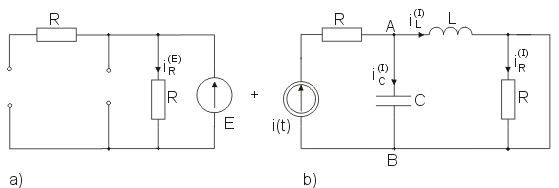
Wyznaczyć rozwiązanie obwodu z rysunku poniżej stosując zasadę superpozycji. Przyjąć , , , , , .
Rozwiązanie
A) Rozwiązanie obwodu dla składowej stałej (źródło )
Obwód dla składowej stałej przedstawiono na rysunku poniżej (a). Cewka w stanie ustalonym dla składowej stałej jest zwarciem a kondensator przerwą.
Dla prądu stałego tylko jeden prąd, , jest różny od zera. Jego wartość jest równa
B) Rozwiązanie obwodu dla składowej zmiennej (źródło )
Obwód dla składowej sinusoidalnej przedstawiono w postaci symbolicznej na (rys. b). Parametry symboliczne obwodu są następujące: , , . Impedancja zastępcza cewki i kondensatora jest równa
Napięcie i prądy w obwodzie:
Wartości prądów wyrażone w postaci czasowej:
Całkowite rozwiązanie obwodu jest sumą obu składowych:
Zadanie 4
Wyznaczyć rozpływy prądów w obwodzie przedstawionym poniżej: