PEE Moduł 13

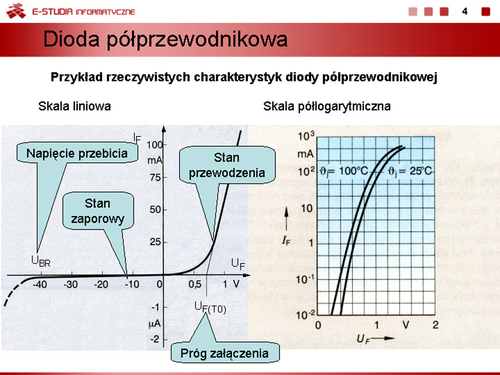
Modele elementów półprzewodnikowych

Wprowadzenie

Do analizy działania i projektowania układów elektronicznych stosuje się odpowiednie modele matematyczne oraz fizyczno-obwodowe elementów półprzewodnikowych wchodzących w skład tych układów. Modele te uwzględniają określone stany pracy, właściwości (np. wpływ temperatury na parametry) i nieliniowość charakterystyk danego elementu.

Rodzaje modeli. Modelem dowolnego urządzenia technicznego nazywamy zbiór informacji umożliwiających przewidywanie właściwości i analizowanie działania tego urządzenia w różnych stanach i warunkach pracy. W elektronice modele mają zazwyczaj postać równań matematycznych lub częściej są w postaci schematów zastępczych równoważnych przyjętym opisom matematycznym. W skład modelu mogą wchodzić dodatkowo charakterystyki prądowo-napięciowe lub inne zależności wielkości elektrycznych i nieelektrycznych poszczególnych przyrządów, elementów, większych podzespołów lub nawet całych układów.

W zależności od stopnia skomplikowania modele fizyczno-obwodowe służą do analizy i projektowania układów elektronicznych bez użycia komputera lub przy jego użyciu. Modele przyrządów półprzewodnikowych można różnie sklasyfikować.

Przyjmując za kryterium zakresy sygnałów jakie wystąpią na zaciskach przyrządu mamy modele:

nieliniowe (dla dużych sygnałów)
liniowe (małosygnałowe).

Ze względu na rodzaj sygnałów są modele:

statyczne (stałoprądowe)
dynamiczne (zmiennoprądowe), które są najczęściej przeznaczone do analizy obwodów w dziedzinie czasu lub częstotliwości.

Inne kryteria podziału mają na celu zaakcentowanie pewnych szczególnych cech przyrządu półprzewodnikowego, np. wpływu temperatury. Mamy tu modele:

izotemperaturowe
nieizotemperaturowe

Modele diod

Dla diod sygnałowych i diod mocy, kiedy pełnią one funkcje jednokierunkowych zaworów, najważniejsze jest zamodelowanie statycznej charakterystyki prądowo-napięciowej. Przykładową charakterystykę rzeczywistej diody przedstawiono na slajdzie. Zaznaczono na niej podstawowe stany pracy diody: stan przewodzenia i stan zaporowy oraz charakterystyczne napięcia: napięcie progu zadziałania i napięcie przebicia. Najczęściej w katalogach podaje się charakterystyki w skali półlogarytmicznej. Ponieważ temperatura ma zasadniczy wpływ na ich przebieg, to temperatura złącza jest tutaj parametrem. Na przykład na slajdzie przedstawiono charakterystyki dla dwóch temperatur $10 0^{\circ} C$ i $2 5^{\circ} C$ .

Do prostych obliczeń charakterystykę diody aproksymuje się trzema odcinkami prostych przyjmując, dla poszczególnych obszarów pracy: przewodzenia, zaporowego i przebicia, charakterystyczne wartości rezystancji. Odcinek charakterystyki w zakresie przebicia (rezystancja

r_{B R}

,) najczęściej nie jest brany pod uwagę, ponieważ podczas normalnej pracy urządzeń, w których zastosowano daną diodę, przebicie napięciowe jest stanem awaryjnym powodującym uszkodzenie urządzenia. Napięcie przebicia

U_{B R}

, nie jest także podawane w katalogach przez producentów elementów półprzewodnikowych.

Ponieważ rezystancja obszaru zaporowego jest bardzo duża, około 107 razy większa od rezystancji w stanie przebicia i przewodzenia to często stosuje się dwuodcinkową aproksymację charakterystyki diody, np. w celu wyznaczenia strat mocy w stanie przewodzenia.

Dla tego modelu w stanie przewodzenia można napisać:

$U_{F} = U_{F (T 0)} + I_{F} r_{F}$

gdzie:

$U_{F (T 0)}$ - napięcie progu załączenia diody,

$r_{F}$ , - rezystancja dynamiczna diody.

Definicję rezystancji dynamicznej diody przedstawiono na slajdzie.

Jeżeli trzeba uwzględnić wsteczny prąd diody modelujemy charakterystykę w sposób przedstawiony na slajdzie 7. W stanie zaporowym dioda jest reprezentowana przez liniowy rezystor

R_{R}

,, a w stanie przewodzenia przez szeregowy obwód składający się ze źródła napięcia modelującego napięcie progu załączenia diody i rezystancji dynamicznej

r_{F}

,. Zatem dla napięć Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_F < U_{F(T0)} napięcie na diodzie można wyznaczyć z zależności <math>U_R = I_R\cdot R_R} , a wstanie przewodzenia napięcie

U_{F}

, jest opisane wzorem dla modelu dwuodcinkowego.

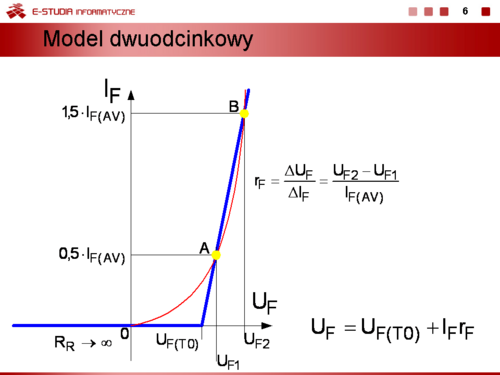
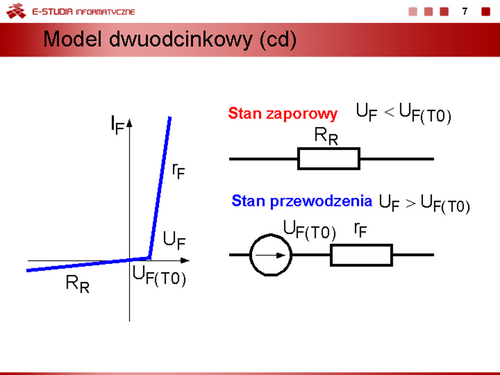
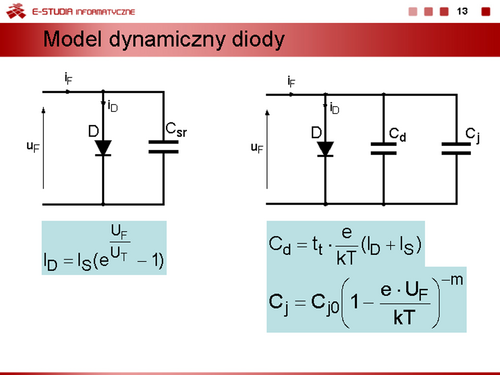
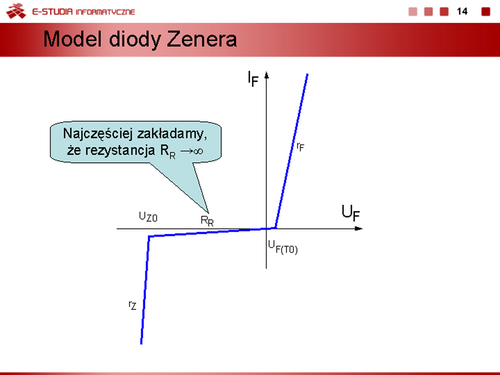
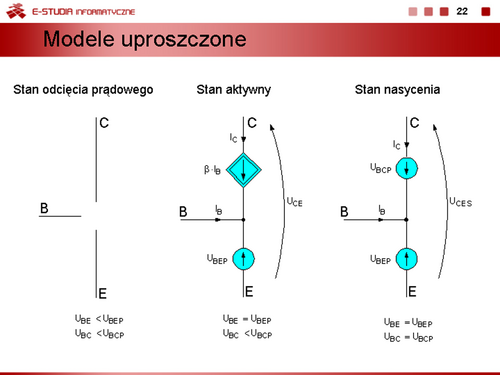
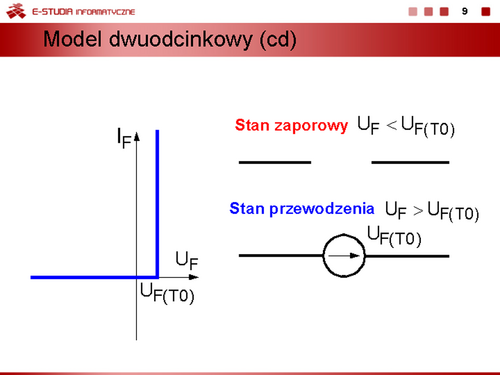
Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym

R_{R} \to \infty

. W stanie przewodzenia nadal obowiązuje wzór dla modelu dwuodcinkowego.

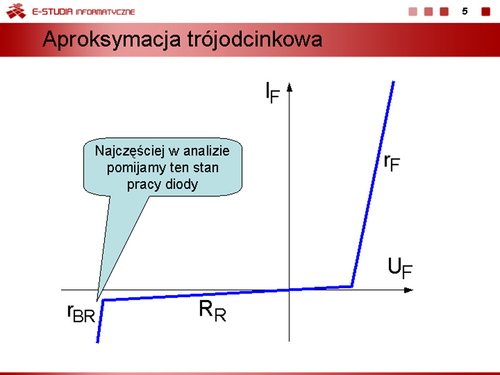
Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. Oznacza to, że rezystancja dynamiczna diody jest równa zeru.

Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony.

Do komputerowej symulacji układów elektronicznych stosuje się inne, bardziej złożone modele, oparte np. na uproszczonej teorii złącza półprzewodnikowego opracowanej przez Shockleya. Zgodnie z tą teorią prąd przewodzenia diody można obliczyć z zależności:

$I_{F} = I_{S} (e^{\frac{U_{F}}{n \cdot U_{T}}} - 1)$

gdzie:

$I_{F}, U_{F}$ , – prąd i napięcie przewodzenia,

$I_{S}$ , – prąd nasycenia płynący przy polaryzacji wstecznej złącza (prąd wsteczny),

$n$ , – współczynnik emisji,

$U_{T} = k T / e$ , - potencjał elektrokinetyczny lub potencjał termiczny elektronu (w temperaturze pokojowej około $25 m V$ ,),

$k$ , - stała Boltzmana $1, 38 \cdot 1 0^{- 23} J / K$ ,

$T$ , – temperatura bezwzględna,

$e$ , – ładunek elementarny $1, 6 \cdot 1 0^{- 19} C$ ,

W ogólnym wypadku prąd nasycenia

I_{S}

, zależy od temperatury złącza zgodnie z zależnością

$I_{S} = C \cdot T^{3} \cdot e^{\frac{- E_{G 0}}{U_{T}}}$

gdzie: $C$ , - stała, $E_{G 0}$ , - jest ekstrapolowaną (dla Parser nie mógł rozpoznać (nieznana funkcja „\diplaystyle”): {\displaystyle \diplaystyle T = 0\, K} ) szerokością przerwy energetycznej ( $1, 19 V$ , dla krzemu, $0, 78 V$ , dla germanu, $1, 56 V$ , dla arsenku galu).

Ze względu na stałą $C$ , w modelach stosowanych w programach komputerowych zależność ta jest unormowana

$I_{S} (T) = I_{S} (T_{0}) \cdot {(\frac{T}{T_{0}})}^{3} \cdot e^{[\frac{E_{G 0}}{U_{T} (T_{0})} (1 - \frac{T_{0}}{T})]}$

Jeżeli zachodzi potrzeba wyznaczenia przebiegów dynamicznych i uwzględnienia procesów bezwładnościowych związanych z gromadzeniem się i usuwaniem ze złącza ładunków, modele statyczne diody można uzupełnić przez dołączenie równolegle do bezinercyjnego modelu diody kondensatorów reprezentujących średnie pojemności dobrane odpowiednio do danego obszaru pracy.

W obliczeniach komputerowych używa się dokładniejszego modelu uwzględniającego pojemność dyfuzyjną złącza $C_{d}$ , i pojemność warstwy zaporowej ( pojemność złączową) $C_{j}$ ,.

$C_{d} = t_{t} \frac{e}{k T} (I_{D} + I_{S})$

gdzie $t_{t}$ , – czas przelotu.

$C_{j} = C_{j 0} {(1 - \frac{U_{R}}{U_{D}})}^{- m} = C_{j 0} {(1 - \frac{e \cdot U_{F}}{k T})}^{- m}$ ,

gdzie $C_{j 0}$ , pojemność złącza przy zerowym napięciu polaryzacji, $m = 0, 5$ , dla złącza skokowego, $m = 0, 333$ , dla złącza liniowego, $U_{R}$ , napięcie wsteczne diody, $U_{D}$ , potencjał dyfuzyjny złącza.

Pojemność złączową można pominąć, gdy spełniony jest warunek $I_{D} > > I_{S}$ .

Do opisu modelu bezinercyjnego stosuje się uproszczony wzór Shockleya

$I_{D} = I_{S} (e^{\frac{U_{F}}{U_{T}}} - 1)$

Przykład 1

Dioda jest w stanie przewodzenia. Prąd $I_{D} = 3 m A$ , temperatura złącza 300 K. Jaka jest konduktancja dynamiczna diody $g_{D}$ , oraz pojemność dyfuzyjna złącza $C_{d}$ ,, jeżeli czas przelotu (stała czasowa) $t_{t} = 5 n s$ .

Rozwiązanie:

Konduktancję diody można wyznaczyć z zależności:

$g_{D} = \frac{1}{r_{D}} = \frac{d I_{D}}{d U_{F}} = \frac{1}{U_{T}} (I_{D} + I_{S})$

Ponieważ w stanie przewodzenia $I_{D} > > I_{S}$ .

$g_{D} \approx \frac{I_{D}}{U_{T}}$

potencjał elektrokinetyczny $U_{T}$ , w temperaturze 300 K jest równy około 26 mV

$U_{T} = \frac{k T}{e} = \frac{1, 38 \cdot 1 0^{- 23} J / K \cdot 300 K}{1, 6 \cdot 1 0^{- 19} C} = 25, 875 m V$

Zatem szukana wartość konduktancji $g_{D}$ , jest równa

$g_{D} \approx \frac{I_{D}}{U_{T}} = \frac{3 m A}{25, 875 m V} = 0, 0116 S \approx 12 m S$

Pojemność dyfuzyjna diody Cd można obliczyć ze wzoru

$C_{d} = t_{t} \frac{e}{k T} (I_{D} + I_{S}) \approx t_{t} \frac{e I_{D}}{k T} = t_{t} \frac{I_{D}}{U_{T}} = t_{t} \cdot g_{0} = 5 n s \cdot 12 m S = 0, 6 n F$

Przykład 2

Wyznaczyć potencjał dyfuzyjny złącza i wykładnik m we wzorze Schottkyego jeżeli dla danych napięć $U_{R}$ , znamy pojemności diody C:

0,4 V – 11 pF, 0 V – 7,4 pF, – 1 V – 4,9 V, – 3 V. – 3,4 pF. W obliczeniach uwzględnić pojemność obudowy diody $C_{0} = 0, 2 p F$

Rozwiązanie:

Metoda prób dobieramy wartość wykładnika m i rysujemy wykres funkcji ${(\frac{1}{C_{j} (U_{R})})}^{- \frac{1}{m}}$ , która powinna być linią prostą. Pojemność złącza obliczamy z zależności Parser nie mógł rozpoznać (błąd składni): {\displaystyle C_j = C – C_0} .

Odp. m = 0,5, $U_{D} = 0, 73 V$ .

Diody Zenera i diody lawinowe. Stabilistory stosuje się w układach stabilizacji napięcia stałego. Dlatego modele jakie tutaj się stosuje są identyczne jak modele bezinercyjne diod sygnałowych i diod mocy. Najczęściej aproksymuje się charakterystykę stabilistora przy pomocy trzech odcinków prostych. Dla napięcia polaryzującego złącze w kierunku przewodzenia odcinek charakterystyki ma nachylenie odpowiadające rezystancji dynamicznej

r_{F}

,, w kierunku wstecznym nachylenie charakterystyki jest określone przez rezystancję dynamiczną

r_{Z}

,.

Czasami zakłada się, że pomiędzy punktami załączenia (napięcie progowe $U_{F (T 0)}$ , w kierunku przewodzenia i przebicia (napięcie przebicia $U_{Z 0}$ ,) dla kierunku polaryzacji zaporowej stabilistor ma rezystancję $R_{R}$ , o kilka rzędów większą niż rezystancje $r_{Z}$ , i $r_{F}$ ,

Najczęściej przyjmuje się, że rezystancja $R_{R} \to \infty$ .

Modele tranzystorów bipolarnych

W ogólnym przypadku napięcia $U_{B E}$ , i $U_{B C}$ , występujące na złączach mogą przyjmować wartości dodatnie i ujemne, a tranzystor może pracować w czterech stanach:

przewodzenia aktywnego, gdy złącze emiterowe przewodzi, a kolektorowe nie przewodzi ( $U_{B E} > 0 V$ , $U_{B C} < 0 V$ )
nasycenia, gdy oba złącza przewodzą ( $U_{B E} > 0 V$ , $U_{B C} > 0 V$ )
przewodzenia inwersyjnego, gdy zamieniono rolami emiter i kolektor tzn. złącze emiterowe nie przewodzi, a kolektorowe przewodzi ( $U_{B E} < 0 V$ , $U_{B C} > 0 V$ )
odcięcia, gdy oba złącza nie przewodzą ( $U_{B E} < 0 V$ , $U_{B C} < 0 V$ )

Na slajdzie przedstawiono rozpływ prądów w tranzystorze npn przy polaryzacji złącza EB w kierunku przewodzenia, a złącza BC w kierunku zaporowym. Ten stan pracy tranzystora nazywamy stanem przewodzenia aktywnego lub stanem aktywnym. Stan ten powszechnie jest wykorzystany w układach wzmacniaczy.

Dla tego stanu można zapisać:

$I_{E} = I_{B} + I_{C} = I_{E S} (e^{\frac{e \cdot U_{B E}}{k \cdot T}} - 1)$

$I_{C} = β_{0} \cdot I_{B} = α_{0} \cdot I_{E}$

$I_{E} = (β_{0} + 1) I_{B} = \frac{I_{C}}{α_{0}}$

Opisowi matematycznemu przedstawionemu na slajdzie 16 odpowiada obwodowy, statyczny, nieliniowy (dla dużych sygnałów) model tranzystora bipolarnego. Przewodzące złącze baza-emiter reprezentuje tutaj dioda opisana równaniem Shockleya, a prąd kolektora zależny wyłącznie od liczby nośników mniejszościowych (elektronów) wstrzykiwanych z obszaru bazy do kolektora jest reprezentowany przez sterowne źródło prądowe

α_{0} \cdot I_{E}

.

Jednym z najczęściej stosowanych podstawowych modeli tranzystora bipolarnego

w zakresie dużych sygnałów uwzględniający wszystkie czterech stany pracy tranzystora bipolarnego jest Model Ebersa-Molla opublikowany przez J. J. Ebersa i J. L. Molla w 1954 roku. Aby wyjaśnić ideę tego modelu załóżmy, że dla tranzystora npn pracującego w stanie nasycenia krzywa rozkładu nośników nadmiarowych $Δ n (x)$ , w bazie ma kształt jak na rysunku przedstawionym na slajdzie 17 i zawiera dwie składowe $Δ n_{N} (x)$ , i $Δ n_{I} (x)$ ,. Oznacza to, że przy pracy tranzystora w stanie nasycenia występuje jednocześnie przepływ elektronów do kolektora wstrzykiwanych przez złącze emiterowe (transmisja normalna, indeks $N$ ,), oraz przepływ elektronów do emitera wstrzykiwanych przez złącze kolektorowe (transmisja inwersyjna, indeks $I$ ,). Dla kierunku transmisji normalnej definiuje się współczynniki wzmocnienia prądowego $α_{N}$ , (lub $β_{N}$ ,), a dla transmisji inwersyjnej $α_{I}$ , (lub $β_{I}$ ,). Wartości odpowiednich współczynników nie są sobie równe, gdyż struktura tranzystora nie jest symetryczna.

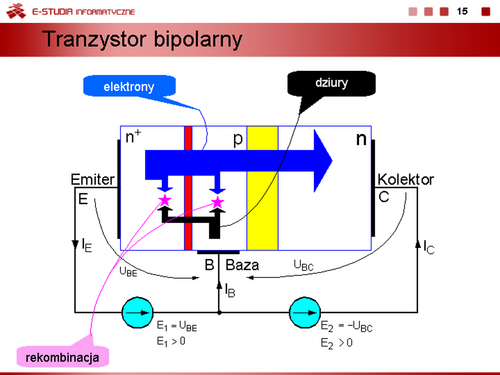
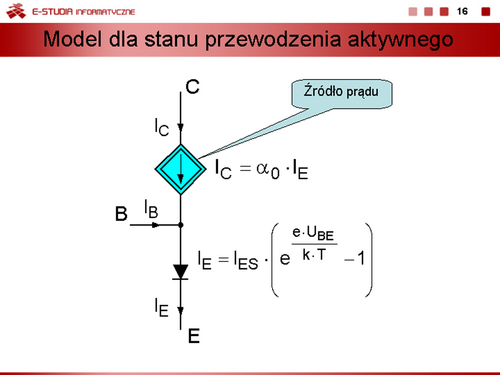
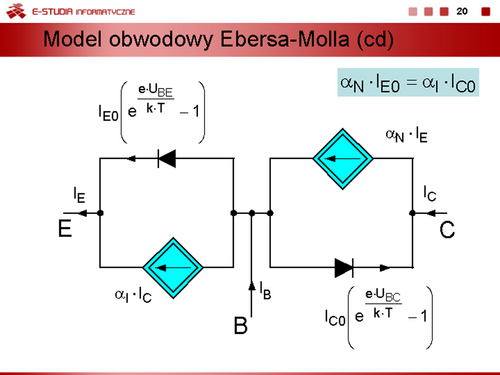
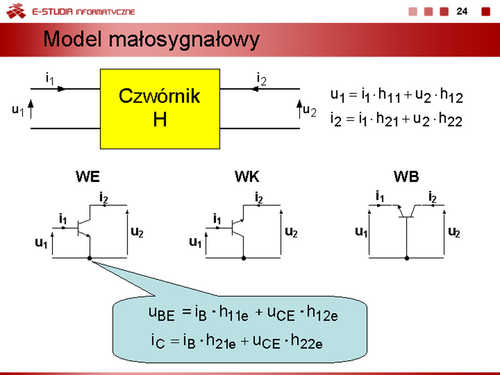
Można zatem zapisać równania, określające związki prądów

I_{C}

,,

I_{E}

, od napięć złączowych

U_{B E}

,,

U_{B C}

, w postaci

$I_{E} = I_{E N} - α_{I} \cdot I_{C I} = I_{E S} (e^{\frac{e \cdot U_{B E}}{k \cdot T}} - 1) - α_{I} \cdot I_{C S} (e^{\frac{e \cdot U_{B C}}{k \cdot T}} - 1)$

$I_{C} = α_{N} \cdot I_{E N} - I_{C I} = α_{N} \cdot I_{E S} (e^{\frac{e \cdot U_{B E}}{k \cdot T}} - 1) - I_{C S} (e^{\frac{e \cdot U_{B C}}{k \cdot T}} - 1)$

Równania te nazywamy równaniami Ebersa-Molla.

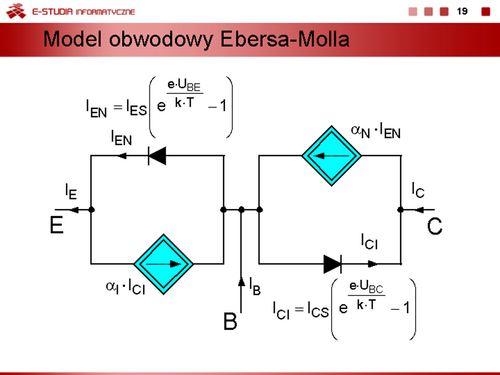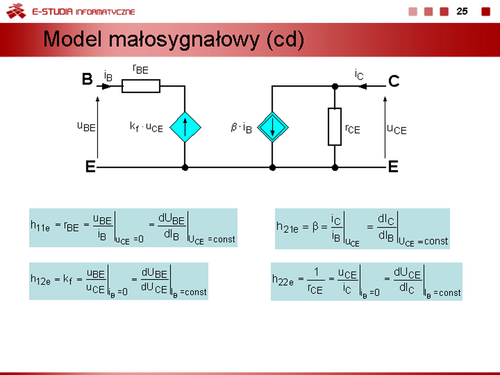
Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19.

Zwykle wygodniej jest posługiwać się modelem Ebersa-Molla, w którym sterowane źródła prądowe są uzależnione od prądów zewnętrznych tranzystora.

$I_{E} = α_{I} \cdot I_{C} + I_{E 0} (e^{\frac{e \cdot U_{B E}}{k \cdot T}} - 1)$

$I_{C} = α_{N} \cdot I_{E} - I_{C 0} (e^{\frac{e \cdot U_{B C}}{k \cdot T}} - 1)$

gdzie $I_{E 0} = (1 - α_{I} \cdot α_{N}) \cdot I_{E S}$

I_{C 0} = (1 - α_{I} \cdot α_{N}) \cdot I_{C S}

Prądy zerowe tranzystora $I_{C 0} = I_{C B 0}, I_{E 0} = I_{C E 0}$ nazywane są także rozwarciowymi prądami nasycenia złącza emiterowego i kolektorowego tranzystora. Można wykazać, że

$α_{N} \cdot I_{E 0} = α_{I} \cdot I_{C 0}$

W wypadku prostych obliczeń wystarczająco dobre jest zastąpienie charakterystyk wejściowej i wyjściowej tranzystora odcinkami prostych podobnie jak to ma miejsce przy modelowaniu diod.

Charakterystyka wejściowa jest aproksymowana trzema odcinkami odpowiednio dla stanu przebicia, zaporowego i przewodzenia. Stan przebicia złącza baza-emiter charakteryzuje napięcie przebicia $U_{B E R}$ ,. Praktycznie zawsze pomijane. Napięcie progowe, przy którym złącze zaczyna przewodzić jest równe $U_{B E P}$ ,, rezystancja odpowiadająca odcinkowi charakterystyki pomiędzy napięciami $U_{B E R}$ , i $U_{B E P}$ , ma wartość $R_{B E}$ ,. Często pomija się ją zakładając, że $R_{B E} \to \infty$ ,. Stan przewodzenia charakteryzuje dynamiczna rezystancja wejściowa tranzystora $r_{B E}$ ,.

Charakterystyki wyjściowe to zbiór prostych równoległych, dla których parametrem jest prąd bazy $I_{B}$ ,. Napięcie $U_{C E S}$ , jest szczątkowym napięciem kolektor-emiter na granicy obszaru aktywnego i obszaru nasycenia. W przybliżeniu jest ono równe różnicy napięć na przewodzących złączach emiterowym i kolektorowym.

$U_{C E S} = U_{B E P} - U_{B C P}$

Ponieważ napięcie $U_{B E P}$ , jest większe od napięcia $U_{B C P}$ , to napięcie $U_{C E S}$ , jest dodatnie. Zwykle przyjmuje się, że ma ono wartość około $0, 2 V$ ,.

Dla poszczególnych odcinków charakterystyk odpowiadających stanom nasycenia, aktywnemu i odcięcia prądowego można narysować obwodowe, linearyzowane schematy zastępcze tranzystora bipolarnego przedstawione na slajdzie 22.

Jeżeli w konkretnym zastosowaniu tranzystora wymagane jest zamodelowanie charakterystyk wyjściowych z uwzględnieniem ich nachylenia, które charakteryzuje dynamiczna rezystancja wyjściowa tranzystora

r_{C E}

, lub jej odwrotność dynamiczna (przyrostowa) konduktancja

g_{C E}

, wykorzystuje się model uwzględniający zjawisko Earlyego. Polega ono na zmianie długości bazy w warstwach zaporowych złączy wnikających w głąb bazy pod wpływem przyłożonego napięcia. W wyniku skracania się bazy przy dużych napięciach kolektor-emiter wzmocnienie prądowe tranzystora zwiększa się, a to objawia się zwiększaniem nachylenia charakterystyk wyjściowych proporcjonalnie do natężenia prądu bazy. Najprościej zjawisko Earlyego uwzględnia się dobierając eksperymentalnie tzw. potencjał Earlyego

U_{E}

,.

Uwzględniając potencjał $U_{E}$ , prąd kolektora można opisać zależnością:

$I_{C} = β_{N 0} (1 + \frac{U_{C E}}{U_{E}}) \cdot I_{B} = β_{Z} \cdot I_{B}$

przy czym $β_{Z} = β_{N 0} (1 + \frac{U_{C E}}{U_{E}})$

$β_{N 0}$ , – ekstrapolowany współczynnik wzmocnienia prądowego tranzystora dla dużych sygnałów wyznaczona przy $U_{C E} = 0 V$ ,.

Znając potencjał Erlyego można wyznaczyć dynamiczną rezystancję wyjściową tranzystora

$r_{C E} = \frac{d U_{C E}}{d I_{C}} |_{I_{B} = c o n s t} \approx \frac{U_{E}}{I_{C}}$

W zakresie małych sygnałów stosuje się modele czwórnikowe tranzystora linearyzujące charakterystyki tranzystora w stanie aktywnym. Linearyzacja polega na zastąpieniu w otoczeniu punktu pracy wybranego odcinka charakterystyk liniami prostymi. Przy takim uproszczeniu wszystkie parametry tranzystora można traktować jako stałe. Z pośród wielu typów macierzy najczęściej jest stosowana macierz hybrydowa h. Opis czwórnika przy wykorzystaniu tej macierzy ma postać

$u_{1} = i_{1} \cdot h_{11} + u_{2} \cdot h_{12}$

$i_{2} = i_{1} \cdot h_{21} + u_{2} \cdot h_{22}$

Schemat zastępczy odpowiadający przyjętemu opisowi przedstawiono na rysunku. Zmiennymi niezależnymi są tutaj prąd wejściowy $i_{1}$ , oraz napięcie wyjściowe $u_{2}$ ,. Ponieważ w przypadku tranzystorów bipolarnych wyróżnia się trzy podstawowe układy pracy: wspólny emiter WE, wspólny kolektor WK, wspólna baza WB to zmienne niezależne macierzy $h$ , przyjmują wartości odpowiedniego prądu wejściowego i napięcia wyjściowego dla przyjętej topologii układu.

Najbardziej popularnym jest układ wspólnego emitera WE, który jest opisany układem równań

$u_{B E} = i_{B} \cdot h_{11 e} + u_{C E} \cdot h_{12 e}$

$i_{C} = i_{B} \cdot h_{21 e} + u_{C E} \cdot h_{22 e}$

Parametry hybrydowe tej macierzy często nazywane parametrami uniwersalnymi są definiowane następująco

$h_{11 e} = r_{B E} = \frac{u_{B E}}{i_{B}} |_{u_{C E} = 0} = \frac{d U_{B E}}{d I_{B}} |_{U_{C E} = c o n s t}$

dynamiczna rezystancja wejściowa w stanie zwarcia na wyjściu,

$h_{12 e} = k_{f} = \frac{u_{B E}}{u_{C E}} |_{i_{B} = 0} = \frac{d U_{B E}}{d U_{C E}} |_{I_{B} = c o n s t}$

współczynnik oddziaływania wstecznego w stanie rozwarcia na wejściu,

$h_{21 e} = β = \frac{i_{C}}{i_{B}} |_{u_{C E = 0}} = \frac{d I_{C}}{d I_{B}} |_{U_{C E} = c o n s t}$

małosygnałowy współczynnik wzmocnienia prądowego w stanie zwarcia na wyjściu,

$h_{22 e} = \frac{1}{r_{C E}} = \frac{u_{C E}}{i_{C}} |_{i_{B} = 0} = \frac{d U_{C E}}{d I_{C}} |_{I_{B} = c o n s t}$

dynamiczna konduktancja (rezystancja) wyjściowa w stanie rozwarcia na wejściu. Schemat zastępczy tranzystora bipolarnego, w którym zastosowano parametry uniwersalne przedstawiono na slajdzie.

Modele tranzystora unipolarnego

Tranzystory JFET i MOSFET mają bardzo podobne charakterystyki. Zarówno dla jednych jak i drugich wyróżnia się zakres pracy liniowej i nieliniowej, które opisane są odpowiednio równaniami

$I_{D} = \frac{I_{D S S}}{U_{P}^{2}} [2 \cdot | U_{G S} - U_{P} | \cdot | U_{D S} | - U_{D S}^{2}]$ dla zakresu pracy liniowej,

$I_{D} = I_{D S S} {(1 - | \frac{U_{G S}}{U_{P}} |)}^{2}$ dla zakresu pracy nieliniowej.

W modelach dla dużych sygnałów wykorzystuje się ten opis matematyczny tranzystora unipolarnego.

W zakresie małych sygnałów, kiedy podobnie jak w wypadku tranzystorów bipolarnych, w okolicy punktu pracy tranzystora można założyć, że charakterystyki są liniowe stosuje się opis macierzowy czwórnika liniowego. Do opisu stosuje się macierz admitancyjną

y

,, dla której zmiennymi niezależnymi są napięcia wejściowe

u_{1}

, i wyjściowe

u_{2}

,.

$i_{1} = u_{1} \cdot y_{11} + u_{2} \cdot y_{12}$

$i_{2} = u_{1} \cdot y_{21} + u_{2} \cdot y_{22}$

Ponieważ tranzystory unipolarne są praktycznie sterowane napięciowo, a ponad to nie wykazują oddziaływania wstecznego (tzn. $y_{11} = y_{12} = 0$ ) w przyjętym opisie pierwsze równanie można pominąć, a w drugim równaniu, w zależności od konfiguracji pracy tranzystora unipolarnego: wspólne źródło WS, wspólny dren WD, wspólna bramka WG, przyjąć za zmienne niezależne odpowiednie napięcia wejściowe i wyjściowe.

Powszechnie przyjmuje się, że podstawą konfiguracją jest układ wspólnego źródła WS, który można opisać równaniami:

$i_{G} = u_{G S} \cdot y_{11 s} + u_{D S} \cdot y_{12 s}$

$i_{D} = u_{G S} \cdot y_{21 s} + u_{D S} \cdot y_{22 s}$

W praktyce częściej zamiast parametrów admitancyjnych stosuje się parametry uniwersalne. Definicje tych parametrów są następujące:

$y_{11 s} = \frac{1}{r_{G S}} = \frac{i_{G}}{u_{G S}} |_{u_{D S} = 0} = \frac{d I_{G}}{d U_{G S}} |_{U_{D S} = c o n s t} = 0$

dynamiczna konduktancja wejściowa przy zwarciu na wyjściu ( $r_{G S} \to \infty$ ),

$y_{12 s} = \frac{i_{G}}{u_{D S}} |_{u_{G S} = 0} = \frac{d I_{G}}{d U_{D S}} |_{U_{G S} = c o n s t} = 0$

oddziaływanie wsteczne (w tranzystorach unipolarnych nie występuje),

$y_{21 s} = S = \frac{i_{D}}{u_{G S}} |_{u_{D S} = 0} = \frac{d I_{D}}{d U_{G S}} |_{U_{D S} = c o n s t}$

transkonduktancja dynamiczna (nachylenie charakterystyki bramkowej) przy zwarciu na wyjściu,

$y_{22 s} = \frac{1}{r_{D S}} = \frac{i_{D}}{u_{D S}} |_{u_{G S} = 0} = \frac{d I_{D}}{d U_{D S}} |_{U_{G S} = c o n s t}$

dynamiczna konduktancja, (rezystancja $r_{D S}$ ,) wyjściowa przy zwarciu na wejściu. Małosygnałowy model tranzystora unipolarnego z zastosowaniem parametrów uniwersalnych przedstawiono na slajdzie.

Literatura

M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005

J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981

P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976

PEE Moduł 13

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia