Sw3.6-m2-1.2-Slajd24
Systemy wbudowane(23)
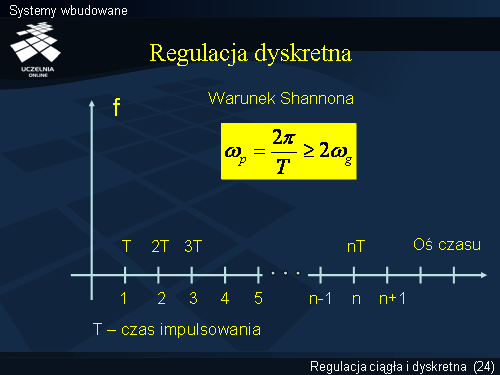
Dotychczasowe rozważania ograniczone były do układów liniowych ciągłych. Stanowią one powszechnie uznany kanon problematyki sterowania i regulacji i na tej podstawie przejdziemy do krótkiego omówienia regulacji dyskretnej. W przypadku regulacji ciągłej wielkości charakterystyczne mają postać funkcji ciągłych (niekoniecznie w całym zakresie zmienności, ale przynajmniej w określonych przedziałach), których wartości są określone w każdej chwili czasu (zmiennej niezależnej). Załóżmy, że znamy wartości funkcji tylko w ściśle określonych chwilach czasowych (najczęściej o stałej odległości) zwanych chwilami impulsowania. Na rysunku opisano oś czasu przyjmując okres impulsowania T. Dla stałej wartości T czas można wtedy wyrazić za pomocą kolejnych liczb naturalnych określających daną chwilę impulsowania.
W praktyce często mamy do czynienia z występowaniem obu rodzajów zależności: ciągłych i dyskretnych. Wówczas stosuje się rozwiązanie będące pewnym kompromisem. Zwykle nie można uzyskać wartości funkcji dyskretnej między poszczególnymi chwilami impulsowania, zatem przyjmuje się rozwiązanie odwrotne, dokonuje się dyskretyzacji funkcji ciągłej. Dyskretyzacja polega na odczytaniu wartości funkcji ciągłej w chwilach impulsowania. Proces ten jednak nie powinien spowodować utraty informacji jaką niesie funkcja ciągła. Podstawowy warunek poprawnej dyskretyzacji funkcji podaje twierdzenie Shannona- Kotielnikowa. . Mówi ono o tym, że każdą funkcję ciągłą f(t), która posiada transformatę Fouriera i której widmo jest ograniczone (tzn. powyżej pulsacji ?g widmo jest równe zeru) można przedstawić w dyskretnych chwilach odległych od siebie o czas T zachowując informację o wartości funkcji w dowolnej chwili, o ile tylko T zostało dobrane zgodnie z warunkiem: T < ?/ ?g.
Warunek ten jest równoważny stwierdzeniu, że częstość próbkowania ?p musi być nie mniejsza niż dwukrotna częstość graniczna ?g .
Taki sposób analizy sygnałów dyskretnych jest charakterystyczny dla systemów komputerowych (mikroprocesorowych) pracujących z określonym cyklem zegarowym. W aplikacjach mikroprocesorowych systemów sterowania czas impulsowania jest wielokrotnością czasu zegara podstawowego procesora.
Sprowadza się to do implementacji programów regulacyjnych dla typowego komputera (mikrokomputera) zaopatrzonego na wejściu i wyjściu odpowiednio w przetworniki A/C i C/A. Sygnałami wejściowymi i wyjściowymi są więc sygnały analogowe, a komputer wykonujący obliczenia tworzy z przetwornikami pewien układ dynamiczny, który może spełniać rolę regulatora. Równanie regulatora i jego współczynniki mogą być łatwo modyfikowane.