MN07

Uwarunkowanie układu równań liniowych

Zajmiemy się wrażliwością układu równań na zaburzenia danych: prawej strony i współczynników macierzy układu. Jak zobaczymu na poniższym przykładzie, bywają równania, które są mało podatne na zaburzenia danych (a więc: dobrze uwarunkowane) oraz równania, które są szalenie wrażliwe na zaburzenia, a więc źle uwarunkowane. Jak wkrótce się przekonamy, czułość danego układu równań na zaburzenia da się precyzyjnie scharakteryzować, a cecha ta nie tylko będzie miała wpływ na jakość rozwiązań możliwych do uzyskania w arytmetyce skończonej precyzji, ale także na efektywność metod iteracyjnych rozwiązywania układów równań liniowych, w których są tysięce (lub więcej) niewiadomych.

Przykład: Uwarunkowanie układu dwóch równań liniowych

Rozwiązanie układu dwóch równań liniowych można przedstawić w formie graficznej: jest to punkt przecięcia się dwóch prostych wyznaczonych przez dane wspólczynniki i wyrazy prawej strony.

Rozważmy pewien nieosobliwy układ dwóch równań liniowych. Ma on dokładnie jedno rozwiązanie, oznaczone kolorem czerwonym. Co się stanie, gdy trochę zaburzymy prawą stronę takiego układu?

Wykresy zaburzonych prostych mogą zająć jedną z zaznaczonych łososiowym kolorem pozycji.

Obszar, gdzie mogą znaleźć się rozwiązania zaburzonego układu, zaznaczyliśmy na czerwono. Jest on, kolokwialnie rzecz ujmując, z grubsza tak wielki jak wielkie były zaburzenia, co zgodne jest z typową intuicją "człowieka z zewnątrz".

Jednak bywają równania, wrażliwe jak mimoza na nawet delikatne zaburzenia danych. Takie równanie własnie widzimy na rysunku: jego cechą szczególną jest to, że tym razem proste, choć wciąż przecinają się dokładnie w jednym punkcie, są prawie równoległe.

Bierzemy zaburzenia takie same jak poprzednio. Wykresy zaburzonych prostych mogą zająć jedną z zaznaczonych łososiowym kolorem pozycji.

Tym razem, obszar niepewności, gdzie mogą być rozwiązania naszego zaburzonego układu, jest gigantyczny!

A więc równania liniowe mogą, choć nie muszą, być bardzo podatne na zaburzenia danych. Gdy zamiast prawej strony, zaburzymy wyrazy macierzy układu, może nawet okazać się, że dostaniemy układ równań sprzecznych (czy możesz podać przykład?)

Aby przedstawić ogólną teorię zaburzeń dla układów równań liniowych, musimy mieć narzędzia do pomiaru błędu rozwiązań, a także zaburzeń danych zadania: czyli macierzy i wektora prawej strony. Temu będą służyć normy.

Normy wektorowe i macierzowe

Aby badać odległość między rozwiązaniem dokładnym układu równań, a jego wartością przybliżoną uzyskaną np. algorytmem eliminacji Gaussa, będziemy posługiwać się normami wektorów Parser nie mógł rozpoznać (nieznana funkcja „\inR”): {\displaystyle \displaystyle x = (x_j)_{j=1}^n\inR^n} i macierzy $A=(a_{i,j}{)}_{i,j=1}^n\in R^{n\times n}$. Najczęściej używanymi normami wektorowymi będą normy $p$-te,

$\Vert x\Vert =\Vert x{\Vert }_p={(\sum _{j=1}^n|x_j{|}^p)}^{1/p},1\le p<+\mathrm{\infty },$

oraz

$\Vert x{\Vert }_{\mathrm{\infty }}=\underset{p\to +\mathrm{\infty }}{\lim }\Vert x{\Vert }_p=\underset{1\le j\le n}{\max }|x_j|.$

Kula jednostkowa w normie $||\cdot |{|}_1$ w $R^2$

Kula jednostkowa w normie $||\cdot |{|}_2$ w $R^2$

Kula jednostkowa w normie $||\cdot |{|}_{\mathrm{\infty }}$ w $R^2$

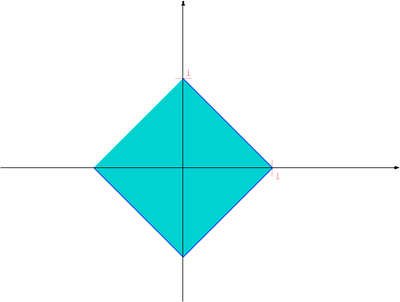
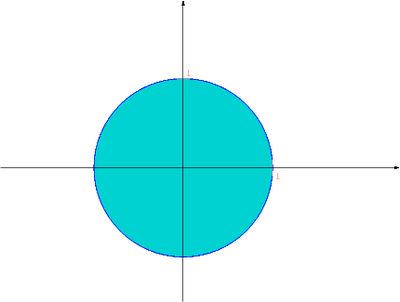
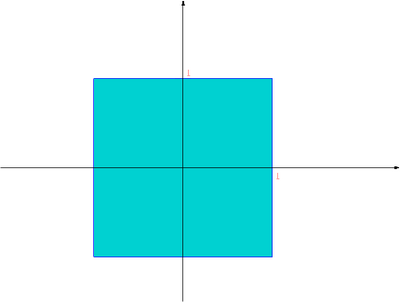
Normą macierzową jest norma euklidesowa (zwana też normą Frobeniusa)

$\Vert A{\Vert }_E=\sqrt{\sum _{i,j=1}^n|a_{i,j}{|}^2},$

a także normy indukowane przez normy wektorowe (np. przez normy $p$-te)

$\Vert A\Vert =\underset{x\ne 0}{\sup }\frac{\Vert Ax\Vert }{\Vert x\Vert }=\underset{\Vert x\Vert =1}{\sup }\Vert Ax\Vert .$

Jeśli norma macierzowa jest indukowana przez normę wektorową, to dla dowolnego wektora mamy

$\Vert Ax\Vert \le \Vert A\Vert \Vert x\Vert .$

Przypomnijmy, że w przestrzeniach liniowych skończenie wymiarowych (a więc także w $R^n$ i w przestrzeni macierzy wymiaru $n\times n$) każde dwie normy są równoważne. To znaczy, że jeśli mamy dwie normy $\Vert \cdot \Vert$ i $\Vert \cdot {\Vert }^{\prime }$ w przestrzeni skończenie wymiarowej $X$, to istnieją stałe $0<K_1\le K_2<\mathrm{\infty }$ takie, że

$K_1\Vert x\Vert \le \Vert x{\Vert }^{\prime }\le K_2\Vert x\Vert ,\mathrm{\forall }x\in X.$

W szczególności dla Parser nie mógł rozpoznać (nieznana funkcja „\inR”): {\displaystyle \displaystyle x\inR^n} mamy

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \| x\|_\infty &\le & \| x\|_1\,\le\, n\,\| x\|_\infty, \\ \| x\|_\infty &\le & \| x\|_2\,\le\, \sqrt{n}\,\| x\|_\infty,\\ \frac 1{\sqrt n}\,\| x\|_1 &\le & \| x\|_2\,\le\, \| x\|_1, \endaligned}

a dla $A=(a_{i,j}{)}_{i,j=1}^n$ mamy

$\Vert A{\Vert }_2\le \Vert |A|{\Vert }_2\le \Vert A{\Vert }_E\le \sqrt{n}\Vert A{\Vert }_2,$

gdzie $|A|=(|a_{i,j}|{)}_{i,j=1}^n$.

Dla macierzy Parser nie mógł rozpoznać (nieznana funkcja „\inR”): {\displaystyle \displaystyle A=(a_{i,j})_{i.j=1}^n\inR^{n\times n}} mamy

$\Vert A{\Vert }_{\mathrm{\infty }}=\underset{1\le i\le n}{\max }\sum _{j=1}^n|a_{i,j}|$

oraz

$\Vert A{\Vert }_1=\Vert A^T{\Vert }_{\mathrm{\infty }}=\underset{1\le j\le n}{\max }\sum _{i=1}^n|a_{i,j}|.$

Dowód tego faktu zostawiamy jako ćwiczenie.

Uwarunkowanie

Wyprowadzimy teraz wynik świadczący o tym, jak zaburzenie względne danych przenosi się na błąd względny wyniku rozwiązania $x^{*}$ układu równań liniowych $Ax=b$.

Twierdzenie O uwarunkowaniu układu równań

Niech $E$ i $e$ będą zaburzeniami odpowiednio macierzy $A$ i wektora $b$ takimi, że

$\Vert E\Vert \le ϵ\Vert A\Vert \text{i}\Vert e\Vert \le ϵ\Vert b\Vert ,$

Jeśli

$ϵ\cdot \text{cond}(A)<1$

to układ zaburzony $(A+E)x=(b+e)$ ma jednoznaczne rozwiązanie $z^{*}$ spełniające

$\frac{\Vert z^{*}-x^{*}\Vert }{\Vert x^{*}\Vert }\le 2\frac{\text{cond}(A)}{1-ϵ\text{cond}(A)}ϵ,$

gdzie definiujemy współczynnik uwarunkowania układu

$\text{cond}(A)=||A||\cdot ||A^{-1}||.$

Zauważmy najpierw, że zachodzi

John von Neumann
Zobacz biografię

Lemat von Neumanna o otwartości zbioru macierzy odwracalnych

Jeśli $F$ jest macierzą taką, że $\Vert F\Vert <1$ to macierz $(I-F)$ jest nieosobliwa oraz

$\Vert (I-F{)}^{-1}\Vert \le \frac{1}{1-\Vert F\Vert }.$

Dowód

Rzeczywiście, gdyby $(I-F)$ była osobliwa to istniałby niezerowy wektor $x$ taki, że $(I-F)x=0$, co implikuje $\Vert Fx\Vert /\Vert x\Vert =1$ i w konsekwencji $\Vert F\Vert \ge 1$. Aby pokazać oszacowanie normy macierzy $(I-F{)}^{-1}$ zauważmy, że

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned 1 &= \|I\|\,=\,\|(I-F)(I-F)^{-1}\| \\ &\ge & \|(I-F)^{-1}\|\,-\,\|F\|\,\|(I-F)^{-1}\| \\ &= (1-\|F\|)\,\|(I-F)^{-1}\|, \endaligned}

skąd już wynika dowodzona nierówność.

Dowód twierdzenia o uwarunkowaniu

Po podstawieniu $F=-A^{-1}E$ mamy teraz

$\Vert F\Vert \le \Vert A^{-1}\Vert \Vert E\Vert \le ϵ\Vert A\Vert \Vert A^{-1}\Vert <1,$

co wobec równości $A+E=A(I+A^{-1}E)$ daje, że macierz $(A+E)$ jest nieosobliwa i układ zaburzony ma jednoznaczne rozwiązanie $z^{*}$. Przedstawmy to rozwiązanie w postaci $z^{*}=x^{*}+(z^{*}-x^{*})$. Rozpisując układ zaburzony i wykorzystując równość $A{x}^{*}=b$ otrzymujemy, że $(A+E)(z^{*}-x^{*})=e-E{x}^{*}$, czyli

$z^{*}-x^{*}=(I+A^{-1}E{)}^{-1}{A}^{-1}(e-E{x}^{*}),$

a stąd

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \| z^*- x^*\| &\le & \|(I+A^{-1}E)^{-1}\|\,\|A^{-1}\| \, (\| e\|+\|E\|\,\| x^*\| \\ &\le & \frac{\|A^{-1}\|}{1-\epsilon\|A\|\,\|A^{-1}\|} \epsilon\left(\| b\|+\|A\|\,\| x^*\|\right) \\ &\le & \frac{\|A\|\,\|A^{-1}\|}{1-\epsilon\|A\|\,\|A^{-1}\|} 2\epsilon\cdot\| x^*\|, \endaligned}

co kończy dowód.

Gdy więc np. $ϵ\text{cond}(A)\le \frac{1}{2}$, powyższe oszacowanie możemy zastąpić czytelniejszym (choć mniej precyzyjnym)

$\frac{\Vert z^{*}-x^{*}\Vert }{\Vert x^{*}\Vert }\le 4\text{cond}(A)ϵ.$

Octave i MATLAB mają wbudowane funkcje wyznaczające normy wektorów i macierzy

 
N = 3;
x = [1:N]'
A = pascal(N)
norm(A,1)
norm(x,2)
norm(A,Inf)

a także funkcje wyznaczające uwarunkowanie macierzy, przy czym Octave liczy tylko uwarunkowanie w normie $||\cdot |{|}_2$:

 
cond(A)

W LAPACKu służy do tego funkcja DGECON. Zadanie wyznaczania uwarunkowania macierzy jest zadaniem bardzo intensywnym numerycznie, a problem, czy da się je wyznaczyć z dobrą dokładnością kosztem niższym niż wyznaczenie macierzy odwrotnej i jej normy, jest wciąż otwarty.

W praktyce obliczeniowej trafiają się zarówno układy dobrze uwarunkowane, jak i macierze, których uwarunkowanie może być patologicznie duże (np. takie macierze są chlebem powszednim osób rozwiązujących równania różniczkowe). Przykładem takiej macierzy o uwarunkowaniu bardzo szybko rosnącym z wymiarem jest m.in.

David Hilbert
Zobacz biografię

Przykład: Macierz Hilberta

Niech $H_N=(h_{ij}{)}_{i,j=1}^N$, gdzie

$h_{ij}=\frac{1}{i+j-1},$

Macierz Hilberta wymiaru 25. Kolor odpowiada rzędowi wielkości elementu macierzy, dokładniej, $\log (h_{ij})$

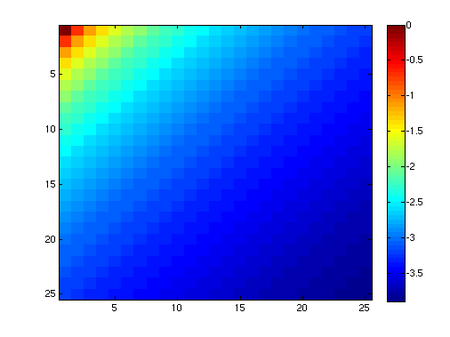
Taką macierz możemy wygenerować w Octave komendą hilb(N). Okazuje się, że uwarunkowanie macierzy Hilberta rośnie bardzo szybko z $N$, $\text{cond}(H_N)\approx O(e^{3.5N})$ , np.

 
octave:2> cond(hilb(5))
ans =  4.7661e+05
octave:3> cond(hilb(10))
ans =  1.6025e+13
octave:4> cond(hilb(15))
ans =  3.7689e+17
octave:5> cond(hilb(20))
ans =  7.1209e+19

Jest to więc bardzo wdzięczna macierz do prowadzenia testów...

Numeryczna poprawność eliminacji Gaussa

Przedstawimy bez dowodu klasyczne twierdzenie o "praktycznej numerycznej poprawności" eliminacji Gaussa z wyborem w kolumnie.

Plik:Wilkinson.jpg

Wilkinson
Zobacz biografię

Twierdzenie Wilkinsona

{{{3}}}

Jak widzimy, kluczowe dla numerycznej poprawności jest oszacowanie wskaźnika wzrostu ${\rho }_N$. Okazuje się, co wiedział już Wilkinson, że

• w najgorszym przypadku, ${\rho }_N\le 2^{N-1}$ i jest osiągane dla macierzy

$W=\left(\begin{array}{cccc}1& & & 1\\ -1& \ddots & & ⋮\\ ⋮& & \ddots & ⋮\\ -1& \cdots & -1& 1\\ \end{array}\right)$

• dla macierzy trójdiagonalnych lub diagonalnie dominujących, lub dla

macierzy symetrycznych dodatnio określonych, ${\rho }_N\le 2$

• w średnim przypadku, obserwuje się ${\rho }_N\le N^{2/3}$, to znaczy macierze

spotykane w praktyce obliczeniowej mają mały wskaźnik wzrostu.

Konkluzja jest więc taka, że algorytm eliminacji Gaussa z wyborem w kolumnie jest praktycznie numerycznie poprawny. Z drugiej strony, dla bardzo dużych $N$ i niezbyt dobrze uwarunkowanych macierzy, może okazać się, że arytmetyka pojedynczej precyzji może okazać się niewystarczająca dla uzyskania godnego wyniku.

Algorytm eliminacji Gaussa z pełnym wyborem elementu głównego jest już w pełni numerycznie poprawny, ze wskaźnikiem wzrostu ${\rho }_N\le \sqrt{n\cdot 2\cdot 3^{1/2}\cdot 4^{1/3}\cdots N^{1/(N-1)}}$, a w praktyce grubo poniżej $\sqrt{N}$.