PEE Moduł 13

Modele elementów półprzewodnikowych

---

Wprowadzenie Do analizy działania i projektowania układów elektronicznych stosuje się odpowiednie modele matematyczne oraz fizyczno-obwodowe elementów półprzewodnikowych wchodzących w skład tych układów. Modele te uwzględniają określone stany pracy, właściwości (np. wpływ temperatury na parametry) i nieliniowość charakterystyk danego elementu.

---

Rodzaje modeli. Modelem dowolnego urządzenia technicznego nazywamy zbiór informacji umożliwiających przewidywanie właściwości i analizowanie działania tego urządzenia w różnych stanach i warunkach pracy. W elektronice modele mają zazwyczaj postać równań matematycznych lub częściej są w postaci schematów zastępczych równoważnych przyjętym opisom matematycznym. W skład modelu mogą wchodzić dodatkowo charakterystyki prądowo-napięciowe lub inne zależności wielkości elektrycznych i nieelektrycznych poszczególnych przyrządów, elementów, większych podzespołów lub nawet całych układów. W zależności od stopnia skomplikowania modele fizyczno-obwodowe służą do analizy i projektowania układów elektronicznych bez użycia komputera lub przy jego użyciu. Modele przyrządów półprzewodnikowych można różnie sklasyfikować. Przyjmując za kryterium zakresy sygnałów jakie wystąpią na zaciskach przyrządu mamy modele: nieliniowe (dla dużych sygnałów) liniowe (małosygnałowe). Ze względu na rodzaj sygnałów są modele: statyczne (stałoprądowe) dynamiczne (zmiennoprądowe), które są najczęściej przeznaczone do analizy obwodów w dziedzinie czasu lub częstotliwości. Inne kryteria podziału mają na celu zaakcentowanie pewnych szczególnych cech przyrządu półprzewodnikowego, np. wpływu temperatury. Mamy tu modele: izotemperaturowe nieizotemperaturowe

---

Modele diod Dla diod sygnałowych i diod mocy, kiedy pełnią one funkcje jednokierunkowych zaworów, najważniejsze jest zamodelowanie statycznej charakterystyki prądowo-napięciowej. Przykładową charakterystykę rzeczywistej diody przedstawiono na slajdzie. Zaznaczono na niej podstawowe stany pracy diody: stan przewodzenia i stan zaporowy oraz charakterystyczne napięcia: napięcie progu zadziałania i napięcie przebicia. Najczęściej w katalogach podaje się charakterystyki w skali półlogarytmicznej. Ponieważ temperatura ma zasadniczy wpływ na ich przebieg, to temperatura złącza jest tutaj parametrem. Na przykład na slajdzie przedstawiono charakterystyki dla dwóch temperatur $100^{\circ }C$ i $25^{\circ }C$.

---

Do prostych obliczeń charakterystykę diody aproksymuje się trzema odcinkami prostych przyjmując, dla poszczególnych obszarów pracy: przewodzenia, zaporowego i przebicia, charakterystyczne wartości rezystancji. Odcinek charakterystyki w zakresie przebicia (rezystancja Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_{BR}\} ,) najczęściej nie jest brany pod uwagę, ponieważ podczas normalnej pracy urządzeń, w których zastosowano daną diodę, przebicie napięciowe jest stanem awaryjnym powodującym uszkodzenie urządzenia. Napięcie przebicia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BR}\} , nie jest także podawane w katalogach przez producentów elementów półprzewodnikowych.

---

Ponieważ rezystancja obszaru zaporowego jest bardzo duża, około 107 razy większa od rezystancji w stanie przebicia i przewodzenia to często stosuje się dwuodcinkową aproksymację charakterystyki diody, np. w celu wyznaczenia strat mocy w stanie przewodzenia. Dla tego modelu w stanie przewodzenia można napisać: $U_F=U_{F(T0)}+I_F{r}_F$ gdzie: $U_{F(T0)}$ - napięcie progu załączenia diody, Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_F\} , - rezystancja dynamiczna diody. Definicję rezystancji dynamicznej diody przedstawiono na slajdzie.

---

Jeżeli trzeba uwzględnić wsteczny prąd diody modelujemy charakterystykę w sposób przedstawiony na slajdzie 7. W stanie zaporowym dioda jest reprezentowana przez liniowy rezystor Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_R\} ,, a w stanie przewodzenia przez szeregowy obwód składający się ze źródła napięcia modelującego napięcie progu załączenia diody i rezystancji dynamicznej Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_F\} ,. Zatem dla napięć Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_F < U_{F(T0)} napięcie na diodzie można wyznaczyć z zależności <math>U_R = I_R\cdot R_R} , a wstanie przewodzenia napięcie Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_F\} , jest opisane wzorem dla modelu dwuodcinkowego.

---

Model dwuodcinkowy uwzględniający warunek, że rezystancja w stanie zaporowym $R_R\to \mathrm{\infty }$. W stanie przewodzenia nadal obowiązuje wzór dla modelu dwuodcinkowego.

---

Kolejne uproszczenie charakterystyki uwzględniające stałą wartość napięcia przewodzenia diody. Oznacza to, że rezystancja dynamiczna diody jest równa zeru.

---

Model idealnej diody. W tym wypadku dioda jest łącznikiem, który w stanie zaporowym jest wyłączony, a w stanie przewodzenia jest załączony.

---

Do komputerowej symulacji układów elektronicznych stosuje się inne, bardziej złożone modele, oparte np. na uproszczonej teorii złącza półprzewodnikowego opracowanej przez Shockleya. Zgodnie z tą teorią prąd przewodzenia diody można obliczyć z zależności: $I_F=I_S(e^{\frac{U_F}{n\cdot U_T}}-1)$ gdzie: Parser nie mógł rozpoznać (błąd składni): {\displaystyle I_F, U_F\} , – prąd i napięcie przewodzenia, Parser nie mógł rozpoznać (błąd składni): {\displaystyle I_S\} , – prąd nasycenia płynący przy polaryzacji wstecznej złącza (prąd wsteczny), Parser nie mógł rozpoznać (błąd składni): {\displaystyle n\} , – współczynnik emisji, Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_T = kT/e\} , - potencjał elektrokinetyczny lub potencjał termiczny elektronu (w temperaturze pokojowej około Parser nie mógł rozpoznać (błąd składni): {\displaystyle 25\, mV\} ,), Parser nie mógł rozpoznać (błąd składni): {\displaystyle k\} , - stała Boltzmana $1,38\cdot 10^{-23}J/K$, Parser nie mógł rozpoznać (błąd składni): {\displaystyle T\} , – temperatura bezwzględna, Parser nie mógł rozpoznać (błąd składni): {\displaystyle e\} , – ładunek elementarny Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1,6\cdot 10^{-19}\, C\} ,

---

W ogólnym wypadku prąd nasycenia Parser nie mógł rozpoznać (błąd składni): {\displaystyle I_S\} , zależy od temperatury złącza zgodnie z zależnością $I_S=C\cdot T^3\cdot e^{\frac{-E_{G0}}{U_T}}$ gdzie: Parser nie mógł rozpoznać (błąd składni): {\displaystyle C\} , - stała, Parser nie mógł rozpoznać (błąd składni): {\displaystyle E_{G0}\} , - jest ekstrapolowaną (dla Parser nie mógł rozpoznać (nieznana funkcja „\diplaystyle”): {\displaystyle \diplaystyle T = 0\, K} ) szerokością przerwy energetycznej (Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1,19\, V\} , dla krzemu, Parser nie mógł rozpoznać (błąd składni): {\displaystyle 0,78\, V\} , dla germanu, Parser nie mógł rozpoznać (błąd składni): {\displaystyle 1,56\, V\} , dla arsenku galu). Ze względu na stałą Parser nie mógł rozpoznać (błąd składni): {\displaystyle C\} , w modelach stosowanych w programach komputerowych zależność ta jest unormowana $I_S(T)=I_S(T_0)\cdot {\left(\frac{T}{T_0}\right)}^3\cdot e^{\left[\frac{E_{G0}}{U_T(T_0)}(1-\frac{T_0}{T})\right]}$

---

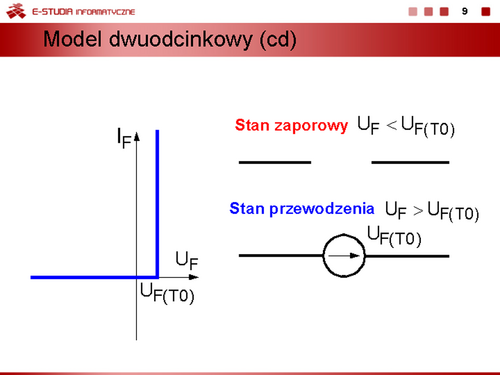
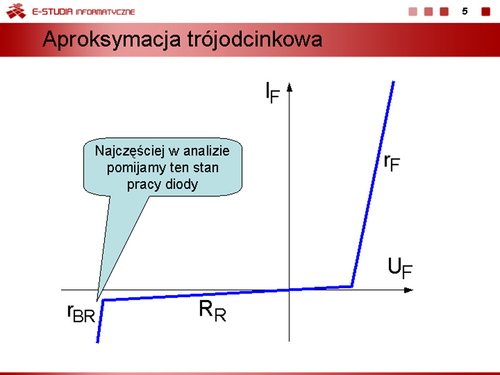
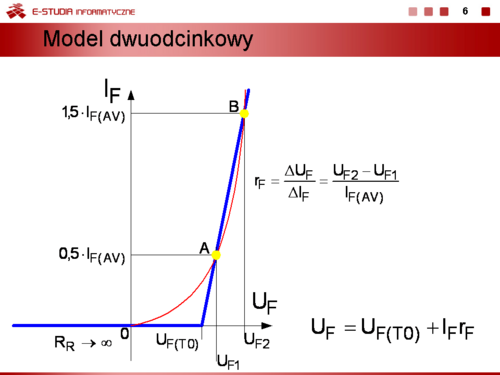
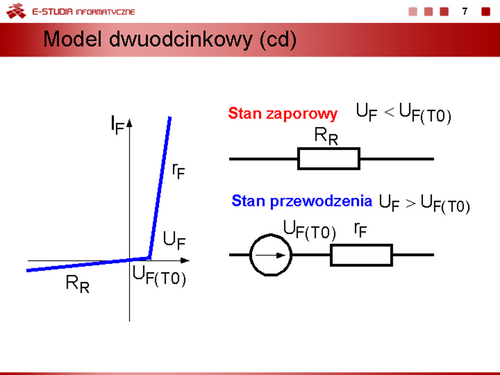
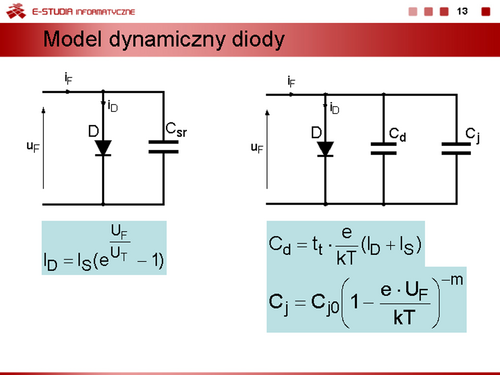
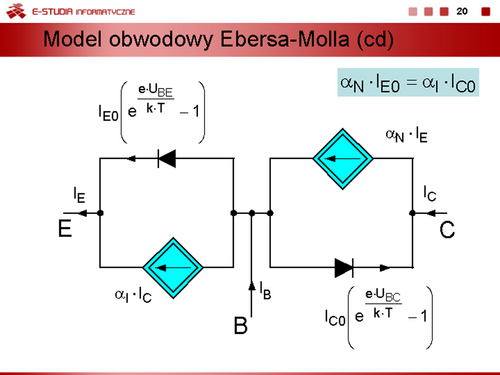
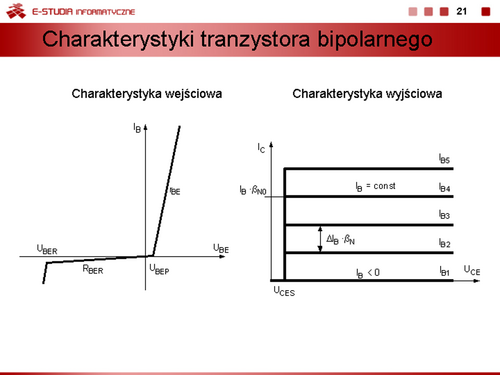
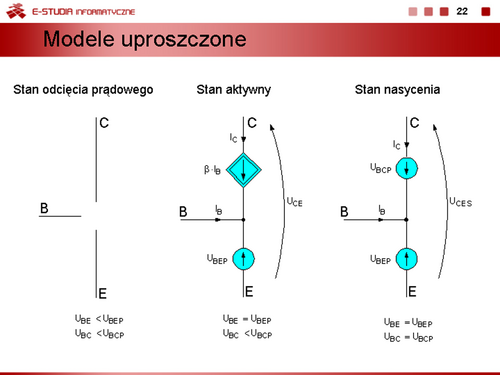
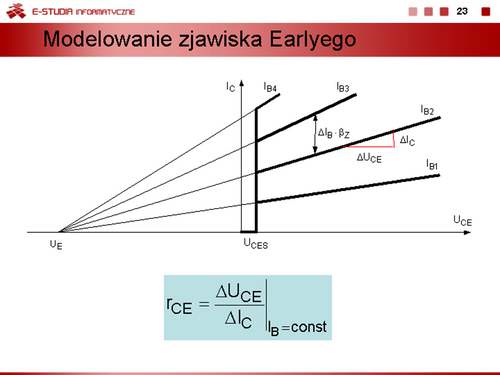
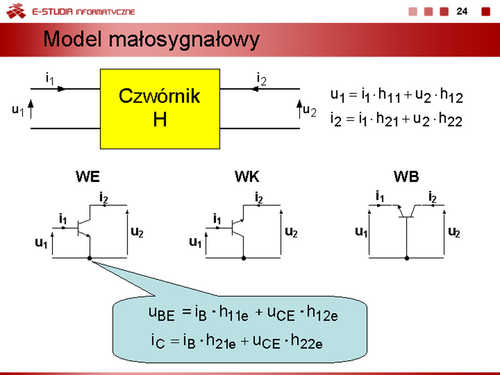
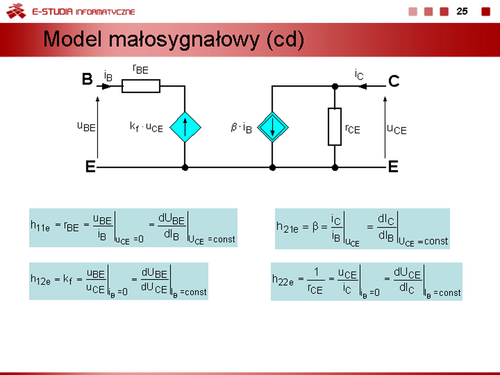
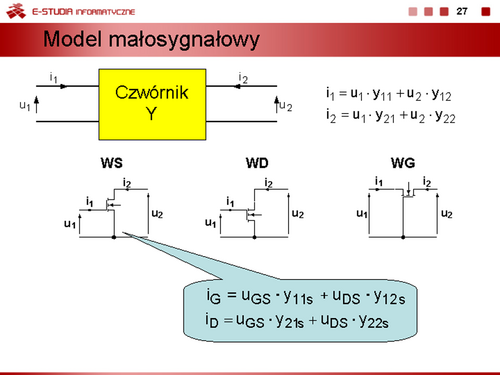
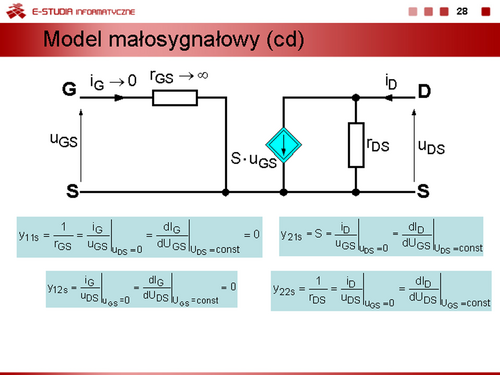
Jeżeli zachodzi potrzeba wyznaczenia przebiegów dynamicznych i uwzględnienia procesów bezwładnościowych związanych z gromadzeniem się i usuwaniem ze złącza ładunków, modele statyczne diody można uzupełnić przez dołączenie równolegle do bezinercyjnego modelu diody kondensatorów reprezentujących średnie pojemności dobrane odpowiednio do danego obszaru pracy. W obliczeniach komputerowych używa się dokładniejszego modelu uwzględniającego pojemność dyfuzyjną złącza Parser nie mógł rozpoznać (błąd składni): {\displaystyle C_d\} , i pojemność warstwy zaporowej ( pojemność złączową) Parser nie mógł rozpoznać (błąd składni): {\displaystyle C_j\} ,. $C_d=t_t\frac{e}{kT}(I_D+I_S)$ gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle t_t\} , – czas przelotu. $C_j=C_{j0}{(1-\frac{U_R}{U_D})}^{-m}=C_{j0}{(1-\frac{e\cdot U_F}{kT})}^{-m}$ , gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle C_{j0}\} , pojemność złącza przy zerowym napięciu polaryzacji, Parser nie mógł rozpoznać (błąd składni): {\displaystyle m = 0,5\} , dla złącza skokowego, Parser nie mógł rozpoznać (błąd składni): {\displaystyle m = 0,333\} , dla złącza liniowego, Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_R\} , napięcie wsteczne diody, Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_D\} , potencjał dyfuzyjny złącza. Pojemność złączową można pominąć, gdy spełniony jest warunek $I_D>>I_S$. 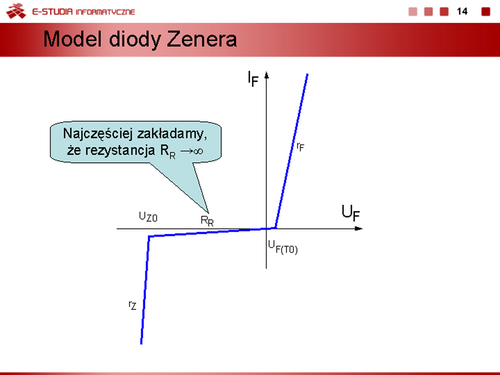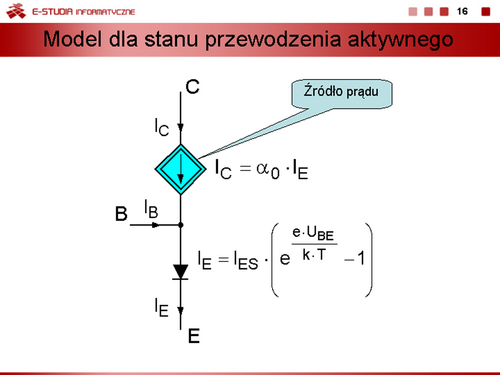Do opisu modelu bezinercyjnego stosuje się uproszczony wzór Shockleya $I_D=I_S(e^{\frac{U_F}{U_T}}-1)$ Przykład 1 Dioda jest w stanie przewodzenia. Prąd $I_D=3mA$, temperatura złącza 300 K. Jaka jest konduktancja dynamiczna diody Parser nie mógł rozpoznać (błąd składni): {\displaystyle g_D\} , oraz pojemność dyfuzyjna złącza Parser nie mógł rozpoznać (błąd składni): {\displaystyle C_d\} ,, jeżeli czas przelotu (stała czasowa) $t_t=5ns$. Rozwiązanie: Konduktancję diody można wyznaczyć z zależności: $g_D=\frac{1}{r_D}=\frac{d{I}_D}{d{U}_F}=\frac{1}{U_T}(I_D+I_S)$ Ponieważ w stanie przewodzenia $I_D>>I_S$. $g_D\approx \frac{I_D}{U_T}$ potencjał elektrokinetyczny Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_T\} , w temperaturze 300 K jest równy około 26 mV $U_T=\frac{kT}{e}=\frac{1,38\cdot 10^{-23}J/K\cdot 300K}{1,6\cdot 10^{-19}C}=25,875mV$ Zatem szukana wartość konduktancji Parser nie mógł rozpoznać (błąd składni): {\displaystyle g_D\} , jest równa $g_D\approx \frac{I_D}{U_T}=\frac{3mA}{25,875mV}=0,0116S\approx 12mS$ Pojemność dyfuzyjna diody Cd można obliczyć ze wzoru $C_d=t_t\frac{e}{kT}(I_D+I_S)\approx t_t\frac{e{I}_D}{kT}=t_t\frac{I_D}{U_T}=t_t\cdot g_0=5ns\cdot 12mS=0,6nF$ Przykład 2 Wyznaczyć potencjał dyfuzyjny złącza i wykładnik m we wzorze Schottkyego jeżeli dla danych napięć Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_R\} , znamy pojemności diody C: 0,4 V – 11 pF, 0 V – 7,4 pF, – 1 V – 4,9 V, – 3 V. – 3,4 pF. W obliczeniach uwzględnić pojemność obudowy diody $C_0=0,2pF$ Rozwiązanie: Metoda prób dobieramy wartość wykładnika m i rysujemy wykres funkcji ${\left(\frac{1}{C_j(U_R)}\right)}^{-\frac{1}{m}}$, która powinna być linią prostą. Pojemność złącza obliczamy z zależności Parser nie mógł rozpoznać (błąd składni): {\displaystyle C_j = C – C_0} . 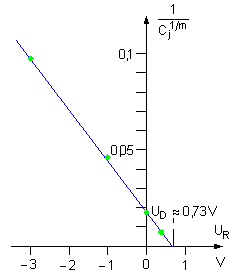Odp. m = 0,5, $U_D=0,73V$.

---

Diody Zenera i diody lawinowe. Stabilistory stosuje się w układach stabilizacji napięcia stałego. Dlatego modele jakie tutaj się stosuje są identyczne jak modele bezinercyjne diod sygnałowych i diod mocy. Najczęściej aproksymuje się charakterystykę stabilistora przy pomocy trzech odcinków prostych. Dla napięcia polaryzującego złącze w kierunku przewodzenia odcinek charakterystyki ma nachylenie odpowiadające rezystancji dynamicznej Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_F\} ,, w kierunku wstecznym nachylenie charakterystyki jest określone przez rezystancję dynamiczną Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_Z\} ,. Czasami zakłada się, że pomiędzy punktami załączenia (napięcie progowe Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{F(T0)}\} , w kierunku przewodzenia i przebicia (napięcie przebicia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{Z0}\} ,) dla kierunku polaryzacji zaporowej stabilistor ma rezystancję Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_R\} , o kilka rzędów większą niż rezystancje Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_Z\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_F\} , Najczęściej przyjmuje się, że rezystancja $R_R\to \mathrm{\infty }$.

---

Modele tranzystorów bipolarnych W ogólnym przypadku napięcia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BE}\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BC}\} , występujące na złączach mogą przyjmować wartości dodatnie i ujemne, a tranzystor może pracować w czterech stanach: przewodzenia aktywnego, gdy złącze emiterowe przewodzi, a kolektorowe nie przewodzi ($U_{BE}>0V$, $U_{BC}<0V$) nasycenia, gdy oba złącza przewodzą ($U_{BE}>0V$, $U_{BC}>0V$) przewodzenia inwersyjnego, gdy zamieniono rolami emiter i kolektor tzn. złącze emiterowe nie przewodzi, a kolektorowe przewodzi ($U_{BE}<0V$, $U_{BC}>0V$) odcięcia, gdy oba złącza nie przewodzą ($U_{BE}<0V$, $U_{BC}<0V$) Na slajdzie przedstawiono rozpływ prądów w tranzystorze npn przy polaryzacji złącza EB w kierunku przewodzenia, a złącza BC w kierunku zaporowym. Ten stan pracy tranzystora nazywamy stanem przewodzenia aktywnego lub stanem aktywnym. Stan ten powszechnie jest wykorzystany w układach wzmacniaczy. Dla tego stanu można zapisać: $I_E=I_B+I_C=I_{ES}(e^{\frac{e\cdot U_{BE}}{k\cdot T}}-1)$ $I_C={\beta }_0\cdot I_B={\alpha }_0\cdot I_E$ $I_E=({\beta }_0+1)I_B=\frac{I_C}{{\alpha }_0}$

---

Opisowi matematycznemu przedstawionemu na slajdzie 16 odpowiada obwodowy, statyczny, nieliniowy (dla dużych sygnałów) model tranzystora bipolarnego. Przewodzące złącze baza-emiter reprezentuje tutaj dioda opisana równaniem Shockleya, a prąd kolektora zależny wyłącznie od liczby nośników mniejszościowych (elektronów) wstrzykiwanych z obszaru bazy do kolektora jest reprezentowany przez sterowne źródło prądowe ${\alpha }_0\cdot I_E$.

---

Jednym z najczęściej stosowanych podstawowych modeli tranzystora bipolarnego w zakresie dużych sygnałów uwzględniający wszystkie czterech stany pracy tranzystora bipolarnego jest Model Ebersa-Molla opublikowany przez J. J. Ebersa i J. L. Molla w 1954 roku. Aby wyjaśnić ideę tego modelu załóżmy, że dla tranzystora npn pracującego w stanie nasycenia krzywa rozkładu nośników nadmiarowych Parser nie mógł rozpoznać (błąd składni): {\displaystyle \Delta n(x)\} , w bazie ma kształt jak na rysunku przedstawionym na slajdzie 17 i zawiera dwie składowe Parser nie mógł rozpoznać (błąd składni): {\displaystyle \Delta n_N(x)\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle \Delta n_I(x)\} ,. Oznacza to, że przy pracy tranzystora w stanie nasycenia występuje jednocześnie przepływ elektronów do kolektora wstrzykiwanych przez złącze emiterowe (transmisja normalna, indeks Parser nie mógł rozpoznać (błąd składni): {\displaystyle N\} ,), oraz przepływ elektronów do emitera wstrzykiwanych przez złącze kolektorowe (transmisja inwersyjna, indeks Parser nie mógł rozpoznać (błąd składni): {\displaystyle I\} ,). Dla kierunku transmisji normalnej definiuje się współczynniki wzmocnienia prądowego Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha_N\} , (lub Parser nie mógł rozpoznać (błąd składni): {\displaystyle \beta_N\} ,), a dla transmisji inwersyjnej Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha_I\} , (lub Parser nie mógł rozpoznać (błąd składni): {\displaystyle \beta_I\} ,). Wartości odpowiednich współczynników nie są sobie równe, gdyż struktura tranzystora nie jest symetryczna.

---

Można zatem zapisać równania, określające związki prądów Parser nie mógł rozpoznać (błąd składni): {\displaystyle I_C\} ,, Parser nie mógł rozpoznać (błąd składni): {\displaystyle I_E\} , od napięć złączowych Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BE}\} ,, Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BC}\} , w postaci $I_E=I_{EN}-{\alpha }_I\cdot I_{CI}=I_{ES}(e^{\frac{e\cdot U_{BE}}{k\cdot T}}-1)-{\alpha }_I\cdot I_{CS}(e^{\frac{e\cdot U_{BC}}{k\cdot T}}-1)$ $I_C={\alpha }_N\cdot I_{EN}-I_{CI}={\alpha }_N\cdot I_{ES}(e^{\frac{e\cdot U_{BE}}{k\cdot T}}-1)-I_{CS}(e^{\frac{e\cdot U_{BC}}{k\cdot T}}-1)$ Równania te nazywamy równaniami Ebersa-Molla.

---

Bezpośrednią interpretacją obwodową równań ze slajdu 18 jest model przedstawiony na slajdzie 19.

---

Zwykle wygodniej jest posługiwać się modelem Ebersa-Molla, w którym sterowane źródła prądowe są uzależnione od prądów zewnętrznych tranzystora. $I_E={\alpha }_I\cdot I_C+I_{E0}(e^{\frac{e\cdot U_{BE}}{k\cdot T}}-1)$ $I_C={\alpha }_N\cdot I_E-I_{C0}(e^{\frac{e\cdot U_{BC}}{k\cdot T}}-1)$ gdzie $I_{E0}=(1-{\alpha }_I\cdot {\alpha }_N)\cdot I_{ES}$ $I_{C0}=(1-{\alpha }_I\cdot {\alpha }_N)\cdot I_{CS}$ Prądy zerowe tranzystora $I_{C0}=I_{CB0},I_{E0}=I_{CE0}$ nazywane są także rozwarciowymi prądami nasycenia złącza emiterowego i kolektorowego tranzystora. Można wykazać, że ${\alpha }_N\cdot I_{E0}={\alpha }_I\cdot I_{C0}$

---

W wypadku prostych obliczeń wystarczająco dobre jest zastąpienie charakterystyk wejściowej i wyjściowej tranzystora odcinkami prostych podobnie jak to ma miejsce przy modelowaniu diod. Charakterystyka wejściowa jest aproksymowana trzema odcinkami odpowiednio dla stanu przebicia, zaporowego i przewodzenia. Stan przebicia złącza baza-emiter charakteryzuje napięcie przebicia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BER}\} ,. Praktycznie zawsze pomijane. Napięcie progowe, przy którym złącze zaczyna przewodzić jest równe Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BEP}\} ,, rezystancja odpowiadająca odcinkowi charakterystyki pomiędzy napięciami Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BER}\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BEP}\} , ma wartość Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_{BE}\} ,. Często pomija się ją zakładając, że Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_{BE} \to \infty\} ,. Stan przewodzenia charakteryzuje dynamiczna rezystancja wejściowa tranzystora Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_{BE}\} ,. Charakterystyki wyjściowe to zbiór prostych równoległych, dla których parametrem jest prąd bazy Parser nie mógł rozpoznać (błąd składni): {\displaystyle I_B\} ,. Napięcie Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{CES}\} , jest szczątkowym napięciem kolektor-emiter na granicy obszaru aktywnego i obszaru nasycenia. W przybliżeniu jest ono równe różnicy napięć na przewodzących złączach emiterowym i kolektorowym. $U_{CES}=U_{BEP}-U_{BCP}$ Ponieważ napięcie Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BEP}\} , jest większe od napięcia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{BCP}\} , to napięcie Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{CES}\} , jest dodatnie. Zwykle przyjmuje się, że ma ono wartość około Parser nie mógł rozpoznać (błąd składni): {\displaystyle 0,2\, V\} ,.

---

Dla poszczególnych odcinków charakterystyk odpowiadających stanom nasycenia, aktywnemu i odcięcia prądowego można narysować obwodowe, linearyzowane schematy zastępcze tranzystora bipolarnego przedstawione na slajdzie 22.

---

Jeżeli w konkretnym zastosowaniu tranzystora wymagane jest zamodelowanie charakterystyk wyjściowych z uwzględnieniem ich nachylenia, które charakteryzuje dynamiczna rezystancja wyjściowa tranzystora Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_{CE}\} , lub jej odwrotność dynamiczna (przyrostowa) konduktancja Parser nie mógł rozpoznać (błąd składni): {\displaystyle g_{CE}\} , wykorzystuje się model uwzględniający zjawisko Earlyego. Polega ono na zmianie długości bazy w warstwach zaporowych złączy wnikających w głąb bazy pod wpływem przyłożonego napięcia. W wyniku skracania się bazy przy dużych napięciach kolektor-emiter wzmocnienie prądowe tranzystora zwiększa się, a to objawia się zwiększaniem nachylenia charakterystyk wyjściowych proporcjonalnie do natężenia prądu bazy. Najprościej zjawisko Earlyego uwzględnia się dobierając eksperymentalnie tzw. potencjał Earlyego Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_E\} ,. Uwzględniając potencjał Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_E\} , prąd kolektora można opisać zależnością: $I_C={\beta }_{N0}(1+\frac{U_{CE}}{U_E})\cdot I_B={\beta }_Z\cdot I_B$ przy czym ${\beta }_Z={\beta }_{N0}(1+\frac{U_{CE}}{U_E})$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle \beta_{N0}\} , – ekstrapolowany współczynnik wzmocnienia prądowego tranzystora dla dużych sygnałów wyznaczona przy Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_{CE} = 0\, V\} ,. Znając potencjał Erlyego można wyznaczyć dynamiczną rezystancję wyjściową tranzystora $r_{CE}=\frac{d{U}_{CE}}{d{I}_C}{|}_{I_B=const}\approx \frac{U_E}{I_C}$

---

W zakresie małych sygnałów stosuje się modele czwórnikowe tranzystora linearyzujące charakterystyki tranzystora w stanie aktywnym. Linearyzacja polega na zastąpieniu w otoczeniu punktu pracy wybranego odcinka charakterystyk liniami prostymi. Przy takim uproszczeniu wszystkie parametry tranzystora można traktować jako stałe. Z pośród wielu typów macierzy najczęściej jest stosowana macierz hybrydowa h. Opis czwórnika przy wykorzystaniu tej macierzy ma postać $u_1=i_1\cdot h_{11}+u_2\cdot h_{12}$ $i_2=i_1\cdot h_{21}+u_2\cdot h_{22}$ Schemat zastępczy odpowiadający przyjętemu opisowi przedstawiono na rysunku. Zmiennymi niezależnymi są tutaj prąd wejściowy Parser nie mógł rozpoznać (błąd składni): {\displaystyle i_1\} , oraz napięcie wyjściowe Parser nie mógł rozpoznać (błąd składni): {\displaystyle u_2\} ,. Ponieważ w przypadku tranzystorów bipolarnych wyróżnia się trzy podstawowe układy pracy: wspólny emiter WE, wspólny kolektor WK, wspólna baza WB to zmienne niezależne macierzy Parser nie mógł rozpoznać (błąd składni): {\displaystyle h\} , przyjmują wartości odpowiedniego prądu wejściowego i napięcia wyjściowego dla przyjętej topologii układu. Najbardziej popularnym jest układ wspólnego emitera WE, który jest opisany układem równań $u_{BE}=i_B\cdot h_{11e}+u_{CE}\cdot h_{12e}$ $i_C=i_B\cdot h_{21e}+u_{CE}\cdot h_{22e}$

---

Parametry hybrydowe tej macierzy często nazywane parametrami uniwersalnymi są definiowane następująco $h_{11e}=r_{BE}=\frac{u_{BE}}{i_B}{|}_{u_{CE}=0}=\frac{d{U}_{BE}}{d{I}_B}{|}_{U_{CE}=const}$ dynamiczna rezystancja wejściowa w stanie zwarcia na wyjściu, $h_{12e}=k_f=\frac{u_{BE}}{u_{CE}}{|}_{i_B=0}=\frac{d{U}_{BE}}{d{U}_{CE}}{|}_{I_B=const}$ współczynnik oddziaływania wstecznego w stanie rozwarcia na wejściu, $h_{21e}=\beta =\frac{i_C}{i_B}{|}_{u_{CE=0}}=\frac{d{I}_C}{d{I}_B}{|}_{U_{CE}=const}$ małosygnałowy współczynnik wzmocnienia prądowego w stanie zwarcia na wyjściu, $h_{22e}=\frac{1}{r_{CE}}=\frac{u_{CE}}{i_C}{|}_{i_B=0}=\frac{d{U}_{CE}}{d{I}_C}{|}_{I_B=const}$ dynamiczna konduktancja (rezystancja) wyjściowa w stanie rozwarcia na wejściu. Schemat zastępczy tranzystora bipolarnego, w którym zastosowano parametry uniwersalne przedstawiono na slajdzie.

---

Modele tranzystora unipolarnego Tranzystory JFET i MOSFET mają bardzo podobne charakterystyki. Zarówno dla jednych jak i drugich wyróżnia się zakres pracy liniowej i nieliniowej, które opisane są odpowiednio równaniami $I_D=\frac{I_{DSS}}{U_P^2}[2\cdot |U_{GS}-U_P|\cdot |U_{DS}|-U_{DS}^2]$ dla zakresu pracy liniowej, $I_D=I_{DSS}{(1-|\frac{U_{GS}}{U_P}\left|\right)}^2$ dla zakresu pracy nieliniowej. W modelach dla dużych sygnałów wykorzystuje się ten opis matematyczny tranzystora unipolarnego.

---

W zakresie małych sygnałów, kiedy podobnie jak w wypadku tranzystorów bipolarnych, w okolicy punktu pracy tranzystora można założyć, że charakterystyki są liniowe stosuje się opis macierzowy czwórnika liniowego. Do opisu stosuje się macierz admitancyjną Parser nie mógł rozpoznać (błąd składni): {\displaystyle y\} ,, dla której zmiennymi niezależnymi są napięcia wejściowe Parser nie mógł rozpoznać (błąd składni): {\displaystyle u_1\} , i wyjściowe Parser nie mógł rozpoznać (błąd składni): {\displaystyle u_2\} ,. $i_1=u_1\cdot y_{11}+u_2\cdot y_{12}$ $i_2=u_1\cdot y_{21}+u_2\cdot y_{22}$ Ponieważ tranzystory unipolarne są praktycznie sterowane napięciowo, a ponad to nie wykazują oddziaływania wstecznego (tzn. $y_{11}=y_{12}=0$) w przyjętym opisie pierwsze równanie można pominąć, a w drugim równaniu, w zależności od konfiguracji pracy tranzystora unipolarnego: wspólne źródło WS, wspólny dren WD, wspólna bramka WG, przyjąć za zmienne niezależne odpowiednie napięcia wejściowe i wyjściowe. Powszechnie przyjmuje się, że podstawą konfiguracją jest układ wspólnego źródła WS, który można opisać równaniami: $i_G=u_{GS}\cdot y_{11s}+u_{DS}\cdot y_{12s}$ $i_D=u_{GS}\cdot y_{21s}+u_{DS}\cdot y_{22s}$

---

W praktyce częściej zamiast parametrów admitancyjnych stosuje się parametry uniwersalne. Definicje tych parametrów są następujące: $y_{11s}=\frac{1}{r_{GS}}=\frac{i_G}{u_{GS}}{|}_{u_{DS}=0}=\frac{d{I}_G}{d{U}_{GS}}{|}_{U_{DS}=const}=0$ dynamiczna konduktancja wejściowa przy zwarciu na wyjściu ($r_{GS}\to \mathrm{\infty }$), $y_{12s}=\frac{i_G}{u_{DS}}{|}_{u_{GS}=0}=\frac{d{I}_G}{d{U}_{DS}}{|}_{U_{GS}=const}=0$ oddziaływanie wsteczne (w tranzystorach unipolarnych nie występuje), $y_{21s}=S=\frac{i_D}{u_{GS}}{|}_{u_{DS}=0}=\frac{d{I}_D}{d{U}_{GS}}{|}_{U_{DS}=const}$ transkonduktancja dynamiczna (nachylenie charakterystyki bramkowej) przy zwarciu na wyjściu, $y_{22s}=\frac{1}{r_{DS}}=\frac{i_D}{u_{DS}}{|}_{u_{GS}=0}=\frac{d{I}_D}{d{U}_{DS}}{|}_{U_{GS}=const}$ dynamiczna konduktancja, (rezystancja Parser nie mógł rozpoznać (błąd składni): {\displaystyle r_{DS}\} ,) wyjściowa przy zwarciu na wejściu. Małosygnałowy model tranzystora unipolarnego z zastosowaniem parametrów uniwersalnych przedstawiono na slajdzie.

---

Literatura

M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005

J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981

P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976