PEE Moduł 9

Wykład 9. Transmitancja operatorowa i charakterystyki częstotliwościowe obwodów

---

Definicja transmitancji operatorowej Weźmy pod uwagę obwód złożony z dowolnych elementów pasywnych RLCM i źródeł sterowanych nie zawierających wewnątrz żadnych źródeł niezależnych. Wyróżnijmy w tym obwodzie jedną parę zacisków uważanych za wejściowe, do których przykładamy źródło wymuszające oraz drugą parę zacisków wyjściowych, z których zbieramy prąd (zaciski zwarte) lub napięcie (zaciski rozwarte). Transmitancja operatorowa określa związek między transformatą operatorową sygnału wyjściowego (odpowiedzi), którą tutaj oznaczymy w ogólności przez Y(s) oraz transformatą operatorową wymuszenia (sygnału wejściowego), oznaczoną ogólnie przez X(s). Transmitancją operatorową nazywać będziemy stosunek transformaty sygnału wyjściowego (prądu lub napięcia) do transformaty sygnału wejściowego układu (źródła napięciowego lub prądowego) przy zerowych warunkach początkowych $T(s)=\frac{Y(s)}{X(s)}$ W zależności od sygnału wejściowego i wyjściowego układu wyróżnić można cztery rodzaje transmitancji operatorowych: transmitancja napięciowa, prądowa, napięciowo-prądowa i prądowo-napięciowa.

---

Przyjmijmy oznaczenie bramy wejściowej cyfrą 1 a bramy wyjściowej cyfrą 2 jak to pokazano na slajdzie 3. Transmitancja napięciowa (napięciowo-napięciowa) Transmitancja napięciowa dotyczy stosunku dwu napięć zewnętrznych układu. Sygnałem wejściowym jest źródło napięciowe, a sygnałem wyjściowym napięcie na dowolnym elemencie uznane za napięcie wyjściowe. Jest ona definiowana w postaci $T_u(s)=\frac{U_2(s)}{U_1(s)}$ W definicji transmitancji napięciowej zakłada się, że napięcie wyjściowe układu mierzone jest w stanie jałowym tzn. przy $Z_0=\mathrm{\infty }$ (bez obciążenia zacisków wyjściowych, $I_2=0$). Transmitancja prądowa (prądowo-prądowa) Transmitancja prądowa dotyczy stosunku dwu prądów zewnętrznych układu, z których jeden jest prądem wymuszającym a drugi prądem gałęzi uznanym za prąd wyjściowy i jest definiowana w postaci $T_i(s)=\frac{I_2(s)}{I_1(s)}$

---

Transmitancja napięciowo-prądowa Transmitancja napięciowo-prądowa przyjmuje napięcie na dowolnym elemencie obwodu jako sygnał wyjściowy Y(s). Sygnałem wejściowym X(s) jest wymuszenie prądowe. Jest zatem zdefiniowana w postaci $T_{ui}(s)=\frac{U_2(s)}{I_1(s)}$ Napięcie $U_2$ mierzone jest w stanie jałowym $(Z_0=\mathrm{\infty })$ obwodu. Transmitancja prądowo-napięciowa Transmitancję prądowo-napięciową definiuje się jako stosunek prądu wyjściowego do napięcia wejściowego (sygnałem wejściowym X(s) jest napięcie wymuszające a sygnałem wyjściowym Y(s) prąd dowolnego elementu w obwodzie) $T_{iu}(s)=\frac{I_2(s)}{U_1(s)}$ Szczególnym przypadkiem transmitancji napięciowo-prądowej jest impedancja wejściowa układu, w definicji której przyjmuje się, że prąd i napięcie dotyczą tej samej bramy wejściowej. Jej definicja jest przyjmowana w postaci $Z_{we}(s)=\frac{U_1(s)}{I_1(s)}$ Definicja impedancji wejściowej układu zakłada dowolny stan obciążenia $Z_0$. Należy jednak zwrócić uwagę, że każda zmiana impedancji obciążenia zmienia impedancję wejściową. Stąd definiując impedancję wejściową należy sprecyzować, przy jakim obciążeniu jest ona wyznaczana. W identyczny sposób można zdefiniować impedancję wyjściową, w której prąd i napięcie dotyczą bramy wyjściowej układu Odwrotność impedancji wejściowej (lub wyjściowej) nazywana jest admitancją wejściową (wyjściową), która może być zinterpretowana jako szczególny przypadek transmitancji prądowo-napięciowej.

---

Transmitancja operatorowa obwodów RLC Przy wyznaczaniu transmitancji operatorowej obwodu zawierającego rezystancje, indukcyjności, indukcyjności sprzężone i pojemności wykorzystuje się model operatorowy poszczególnych elementów R, L, C i M wprowadzony w lekcji poprzedniej. Przy założeniu zerowych warunków początkowych dla indukcyjności i pojemności modele tych elementów nie zawierają źródeł a jedynie impedancje operatorowe Z(s). Zestaw impedancji operatorowych dla elementów pasywnych przedstawiono na slajdzie 5. Dla obwodów pasywnych zawierających elementy R, L, C i M obliczenie transmitancji operatorowej polega na zastąpieniu elementu rzeczywistego poprzez ich impedancje operatorowe a następnie wykorzystując dowolną metodę analizy (metoda praw Kirchhoffa, węzłowa, oczkowa, Thevenina, Nortona) należy wyznaczyć odpowiedź operatorową w funkcji wymuszenia. Wobec liniowości obwodu każda jego odpowiedź (dowolny prąd i dowolne napięcie) jest liniową funkcją wymuszenia. Obliczając transmitancję dzieli się odpowiedź przez wymuszenie, w wyniku czego zmienna będąca wymuszeniem ulega redukcji i w efekcie transmitancja zależy wyłącznie od parametrów RLC obwodu oraz źródeł sterowanych, będąc jednocześnie funkcją zmiennej zespolonej s. Metodę wyznaczania transmitancji operatorowej zilustrujemy na przykładzie obwodu LC przedstawionego na slajdzie 8. W ogólnym przypadku obwodu elektrycznego liniowego zawierającego rezystory, cewki i kondensatory oraz źródła sterowane dowolna transmitancja operatorowa ma postać funkcji wymiernej o stopniu licznika równym m i stopniu mianownika równym n $T(s)=\frac{L(s)}{M(s)}=\frac{b_m{s}^m+b_{m-1}{s}^{m-1}+\cdots +b_{1}s+b_0}{s^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0}$ Współczynniki $a_i$ mianownika oraz $b_i$ licznika są funkcjami parametrów elementów obwodu i dla ich konkretnych wartości przyjmują wartości rzeczywiste. Najwyższy stopień wielomianu jest równy (w szczególnych przypadkach mniejszy) liczbie elementów reaktancyjnych (cewek i kondensatorów) obwodu. Najczęściej w obwodach występujących w praktyce stopień mianownika jest nie mniejszy niż stopień licznika. Pojęcie impedancji operatorowej jest uogólnieniem impedancji zespolonej elementów stosowanej w metodzie symbolicznej przy analizie stanów ustalonych w obwodzie zawierającym wymuszenia sinusoidalne. Łatwo pokazać to zakładając $s=j\omega$ we wzorach określających odpowiednie impedancje operatorowe. Dla elementów indukcyjnych i pojemnościowych przy założeniu $s=j\omega$ otrzymuje się następujące zależności $Z_L(s){|}_{s=j\omega }=j\omega L=Z_L(j\omega )$ $Z_M(s){|}_{s=j\omega }=\pm j\omega M=Z_M(j\omega )$ $Z_C(s){|}_{s=j\omega }=\frac{1}{j\omega C}=Z_C(j\omega )$ Impedancje $Z(j\omega )$ reprezentują impedancje symboliczne elementów RLC, obowiązujące w analizie stanów ustalonych przy wymuszeniach sinusoidalnych. Założenie $s=j\omega$ upraszcza zatem opis obwodu w stanie nieustalonym do opisu obwodu w stanie ustalonym przy założeniu wymuszenia sinusoidalnego.

---

Odpowiedź impulsowa i skokowa układu Opis obwodu w dziedzinie zmiennej zespolonej s pozwala badać jego zachowanie przy pobudzeniu dowolnym wymuszeniem. Szczególnie ważne są właściwości dynamiczne obwodów (stan nieustalony) przy pobudzeniu za pomocą pewnych wymuszeń standardowych. Do takich wymuszeń należy impuls Diraca $\delta (t)$ oraz funkcja skoku jednostkowego $1(t)$. Odpowiedź impulsowa Odpowiedzią impulsową układu nazywamy jego odpowiedź czasową na wymuszenie w postaci impulsu Diraca przy zerowych warunkach początkowych obwodu. Dla wyznaczenia odpowiedzi impulsowej wykorzystuje się pojęcie transmitancji operatorowej T(s). Transformata funkcji impulsowej Diraca jest równa 1, zatem obliczając odpowiedź obwodu przyjmiemy wymuszenie X(s)=1. Bezpośrednio z definicji transmitancji wynika $T(s)=\frac{Y(s)}{X(s)}=\frac{Y(s)}{1}\to Y(s)=T(s)$ Odpowiedź impulsowa układu jest transformatą odwrotną Laplace’a sygnału Y(s). Stąd $y(t)=L^{-1}[Y(s)]=L^{-1}[T(s)]$ Z powyższej zależności wynika, że odpowiedź impulsowa jest transformatą odwrotną Laplace’a transmitancji operatorowej T(s) układu. Odpowiedź skokowa Odpowiedzią skokową układu nazywamy odpowiedź czasową tego układu na wymuszenie w postaci skoku jednostkowego $1(t)$ przy zerowych warunkach początkowych obwodu. Biorąc pod uwagę, że transformata Laplace’a funkcji jednostkowej $1(t)$ jest równa $1/s$ otrzymuje się $T(s)=\frac{Y(s)}{X(s)}=\frac{Y(s)}{1/s}\to Y(s)=\frac{1}{s}T(s)$ Odpowiedź skokowa jest transformatą odwrotną Laplace’a sygnału Y(s). Stąd $y(t)=L^{-1}[Y(s)]=L^{-1}[\frac{1}{s}T(s)]$ Odpowiedź skokowa układu jest więc transformatą odwrotną Laplace’a transmitancji operatorowej T(s) tego układu, podzielonej przez zmienną zespoloną s. Podobnie jak odpowiedź impulsowa odpowiedź skokowa jest określona w pełni przez transmitancję operatorową T(s) układu.

---

Przykład Dla zilustrowania rozważań teoretycznych obliczmy odpowiedź impulsową i skokową układu o zadanej transmitancji operatorowej $T(s)=\frac{1}{(s+1)(s+5)}$ Rozwiązanie Stosując metodę residuów dla zadanej postaci transmitancji T(s) otrzymujemy: odpowiedź impulsową $h(t)=L^{-1}\left[\frac{1}{(s+1)(s+5)}\right]=$ $=li{m}_{s\to -1}\frac{1}{s+5}{e}^{st}+li{m}_{s\to -5}\frac{1}{s+1}{e}^{st}=$ $=\frac{1}{4}{e}^{-t}-\frac{1}{4}{e}^{-5t}$ odpowiedź skokową $y(t)=L^{-1}\left[\frac{1}{s(s+1)(s+5)}\right]=$ $=li{m}_{s\to 0}\frac{1}{(s+1)(s+5)}{e}^{st}+li{m}_{s\to -1}\frac{1}{s(s+5)}{e}^{st}+$ $+li{m}_{s\to -5}\frac{1}{s(s+1)}{e}^{st}=$ $=0,2-0,25e^{-t}+0,05e^{-5t}$

---

Na slajdzie 9 przedstawiono wykres czasowy odpowiedzi impulsowej i skokowej układu o zadanej postaci transmitancji operatorowej T(s).

---

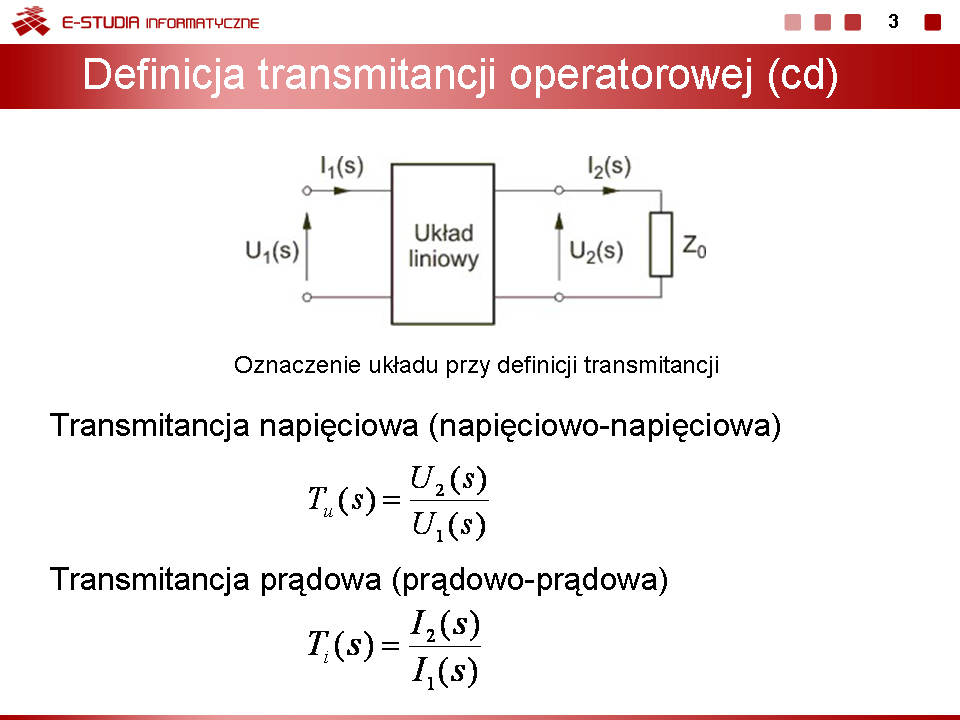
Stabilność układów liniowych Opis układów liniowych za pomocą transmitancji operatorowej bądź równoważny mu opis równaniami stanu pozwala badać cechy jakościowe układu na podstawie analizy położenia jego biegunów (wartości własnych macierzy stanu). Do najważniejszych cech układu należą pojęcie stabilności oraz charakter odpowiedzi układu w stanie przejściowym na skutek przyłożenia wymuszenia zewnętrznego. 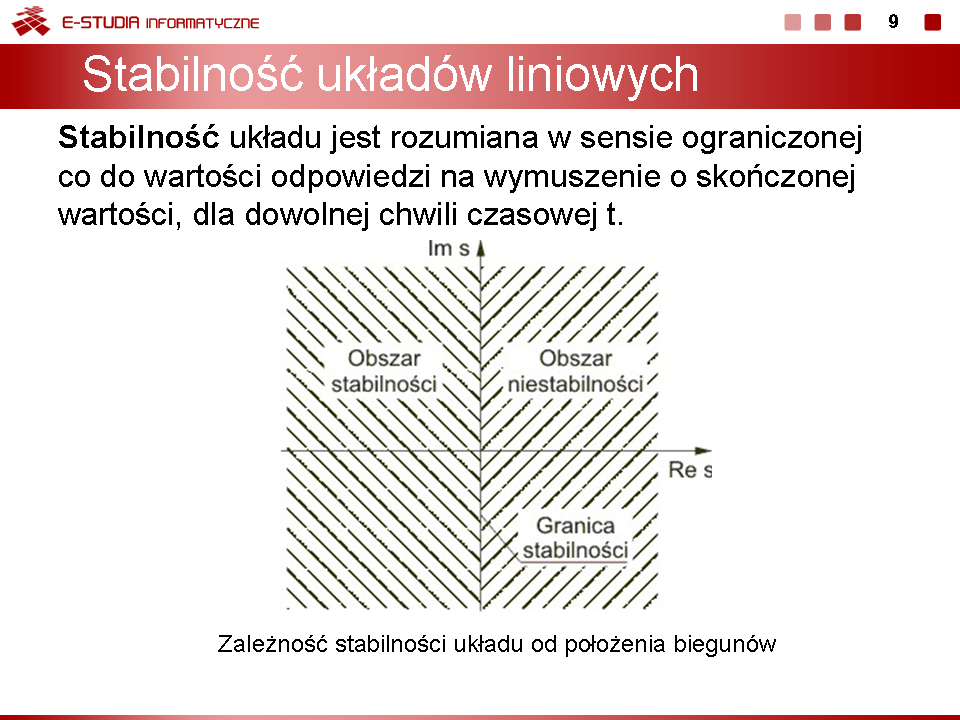Stabilność układu jest rozumiana w sensie ograniczonej co do wartości odpowiedzi na wymuszenie o skończonej wartości, dla dowolnej chwili czasowej t. Układ nazywać będziemy stabilnym, jeśli jego odpowiedź czasowa na skończoną wartość pobudzenia będzie ograniczona co do wartości w dowolnej chwili czasowej t. Stabilność wymaga, aby przy zaniku pobudzenia odpowiedź układu w stanie ustalonym przy $t\to \mathrm{\infty }$ była ograniczona co do wartości (stabilność w sensie zwykłym) lub zerowa (stabilność w sensie asymptotycznym). Oznacza to, że dla układów stabilnych odpowiedź w stanie przejściowym powinna zanikać do zera lub co najmniej nie narastać, pozostając na ustalonym poziomie. Stabilność układu może więc być oceniana na podstawie odpowiedzi impulsowej. Jeśli odpowiedź ta zanika do zera lub pozostaje na stałym poziomie przy $t\to \mathrm{\infty }$ układ jest stabilny. Jeśli natomiast odpowiedź impulsowa ma charakter narastający w czasie – układ jest niestabilny. Zauważmy, że odpowiedź impulsowa jest transformatą odwrotną Laplace’a transmitancji operatorowej $h(t)=L^{-1}[T(s)]$ Jeśli bieguny układu oznaczymy przez $s_i$ gdzie i = 1, 2, ..., n, wówczas w przypadku biegunów jednokrotnych na podstawie metody residuów odpowiedź impulsowa może być wyrażona wzorem $h(t)=\sum _{i=1}^n{A}_i{e}^{s_{i}t}$ Wzór ten dowodzi, że jeśli wszystkie bieguny układu są położone wyłącznie w lewej półpłaszczyźnie zmiennej zespolonej s, $R(s_i)\le 0$, wówczas odpowiedź impulsowa zanika z czasem do zera lub pozostaje ograniczona co do amplitudy (gdy część biegunów lub wszystkie znajdą się na osi urojonej). Sytuacja jest nieco bardziej złożona, gdy część biegunów jest wielokrotna. Dla uproszczenia ograniczymy się tylko do biegunów dwukrotnych. Załóżmy, że liczba takich dwukrotnych biegunów jest równa m. W takim przypadku zastosowanie wzorów na residuum przy obliczaniu transformaty odwrotnej prowadzi do wyniku $y(t)=\sum _{i=1}^n{A}_i{e}^{s_{i}t}+\sum _{k=1}^m{B}_{k}t{e}^{s_{k}t}$ Przy niezerowej wartości części rzeczywistej biegunów położonych w lewej półpłaszczyźnie odpowiedź przejściowa układu przy $t\to \mathrm{\infty }$ będzie zanikać do zera (układ stabilny asymptotycznie). Przy położeniu biegunów na osi urojonej $R(s_i)=0$ układ może być stabilny (choć nie asymptotycznie), jeśli są to bieguny pojedyncze lub niestabilny, jeśli bieguny są wielokrotne. Utrata stabilności na skutek położenia bieguna wielokrotnego na osi urojonej wynika z pojawienia się we wzorze na odpowiedź impulsową czynnika proporcjonalnego do czasu. Zauważmy, że przy spełnieniu warunku $Re(s_k)=0$ i założeniu bieguna zespolonego $s_k=j\omega$ wyrażenie $B_{k}t{e}^{s_{k}t}$ może być rozwinięte do postaci $B_{k}t{e}^{s_{k}t}=B_{k}t(cos\omega t+jsin\omega t)$. Wobec ograniczonych wartości funkcji sinus i cosinus czynnik ten przy $t\to \mathrm{\infty }$ narasta nieograniczenie, co prowadzi do utraty stabilności. W konsekwencji warunkiem stabilności układu jest położenie biegunów w lewej półpłaszczyźnie, a w przypadku biegunów wielokrotnych wyłączenie ich z osi urojonej.

---

Na slajdzie 9 zilustrowano wpływ położenia biegunów na stabilność układu. Oś urojona rozgraniczająca obszar stabilny od niestabilnego jest obszarem warunkowo stabilnym (stabilny w sensie zwykłym przy biegunach jednokrotnych i niestabilny przy biegunach wielokrotnych). Interesujący jest również wpływ położenia biegunów na charakter odpowiedzi impulsowej układu liniowego. Slajd 10 przedstawia odpowiedzi impulsowe układu drugiego rzędu przy różnych położeniach biegunów. W zależności od wartości biegunów mamy do czynienia ze stanem aperiodycznym (bieguny położone na osi rzeczywistej) oraz oscylacyjnym (bieguny zespolone). Zanikanie odpowiedzi impulsowej do zera świadczy o stabilności asymptotycznej układu. Odpowiedź o ograniczonej amplitudzie nie zanikająca z czasem świadczy o stabilności zwykłej układu. Odpowiedź narastająca z czasem jest cechą układu niestabilnego.

---

Charakterystyki częstotliwościowe układów Charakterystyką częstotliwościową układu nazywać będziemy zależność wartości sygnału wyjściowego tego układu od częstotliwości przy jednostkowym wymuszeniu sinusoidalnym przyłożonym na wejście układu. Charakterystykę tę można wyznaczyć bezpośrednio na podstawie transmitancji operatorowej T(s). Nosi ona nazwę transmitancji widmowej układu. Oznaczmy transmitancję widmową w postaci $T(j\omega )$. Jest ona zdefiniowana jako transmitancja operatorowa dla $s=j\omega$, to znaczy $T(j\omega )=T(s){|}_{s=j\omega }$ Transmitancja widmowa reprezentuje sobą liczbę zespoloną będącą funkcją pulsacji $\omega$. Przedstawiając ją w postaci wykładniczej, to jest $T(j\omega )=|T(j\omega )|e^{j\phi (\omega )}$ można zdefiniować dwa rodzaje charakterystyk częstotliwościowych: charakterystyka amplitudowa przedstawia sobą zależność modułu transmitancji widmowej $T(j\omega )$ od pulsacji $\omega$ (częstotliwości f), to jest $|T(j\omega )|$ charakterystyka fazowa określa zależność argumentu transmitancji widmowej $T(j\omega )$ od pulsacji (częstotliwości) to jest $\phi (\omega )$. Charakterystyka fazowa reprezentuje sobą przesunięcie fazowe między sygnałem wejściowym a wyjściowym dla danej pulsacji $\omega$. Charakterystyki częstotliwościowe przedstawia się zwykle na wykresie modułu lub fazy w zależności od pulsacji (częstotliwości). Jeśli wielkości podlegające wykreślaniu różnią się znacznie pod względem wartości (np. zmieniają się w zakresie od $1$ do $10^6$) wygodnie jest wprowadzić skalę logarytmiczną zwykle o podstawie 10. Dotyczy to określonego zakresu częstotliwości. W przypadku charakterystyki amplitudowej skalę logarytmiczną przelicza się na decybele (dB) definiując logarytmiczną charakterystykę amplitudową $20lo{g}_{10}(|T(j\omega )|)$

---

Przykład Jako przykład rozpatrzmy transmitancję operatorową opisaną wzorem $T(s)=\frac{0,003s^4+0,082s^2+0,287}{s^4+0,945s^3+1,487s^2+0,778s+0,322}$ Charakterystyka amplitudowa jest określona wzorem $T(s)=\frac{0,003{\omega }^4-0,082{\omega }^2+0,287}{({\omega }^4-1,487{\omega }^2+0,322)+j(-0,945{\omega }^3+0,778\omega )}$ Na slajdzie 12 przedstawiono przykładowo charakterystykę amplitudową oraz logarytmiczną charakterystykę amplitudową odpowiadającą transmitancji danej wzorem Każdy rodzaj przedstawienia charakterystyki amplitudowej podkreśla inne szczegóły w jej przebiegu. Charakterystyka logarytmiczna podkreśla stosunkowo niewielkie w skali globalnej zmiany dynamiczne w tak zwanym paśmie zaporowym, gdzie amplituda sygnału jest bardzo mała w stosunku do pasma przepustowego, podczas gdy skala liniowa uwypukla globalny charakter przebiegu tracąc drobne szczegóły w zakresie częstotliwości gdzie wartości sygnałów są małe. Charakterystyka amplitudowa wskazuje na dobre (nie tłumione) przenoszenie częstotliwości małych. W miarę wzrostu wartości częstotliwości charakterystyka amplitudowa maleje, co oznacza, że sygnał wyjściowy ma coraz mniejszą amplitudę. Taki obwód ma więc charakter układu dolnoprzepustowego (szeregowo włączona cewka w miarę wzrostu częstotliwości ma coraz większą impedancję tłumiącą przebieg prądu przepływającego przez rezystor wyjściowy).

---

Przykłady transmitancji operatorowych pierwszego rzędu W praktyce inżynierskiej zdefiniowano wiele użytecznych postaci transmitancji operatorowych. Tutaj ograniczymy się jedynie do trzech najprostszych transmitancji pierwszego rzędu: układu całkującego, różniczkującego oraz przesuwnika fazowego. Układ całkujący Transmitancja idealnego układu całkującego definiowana jest w postaci $T(s)=\frac{k}{s}$ Układ nosi nazwę całkującego, gdyż operator 1/s w dziedzinie częstotliwości zespolonej Laplace’a oznacza całkowanie funkcji w dziedzinie czasu. Charakterystykę częstotliwościową układu całkującego opisuje zależność $T(j\omega )=\frac{k}{j\omega }=\frac{k}{\omega }{e}^{-j90^{\circ }}$ Wykres charakterystyki amplitudowej $|T(j\omega )|=\frac{k}{\omega }$ oraz fazowej $\phi (\omega )=-90^{\circ }$ dla układu całkującego przy k>0 przedstawiono na slajdzie 13. Charakterystyka amplitudowa jest typu hiperbolicznego, a charakterystyka fazowa stała (przesunięcie fazowe stałe i równe $-90^{\circ }$ niezależnie od częstotliwości).

---

Układ różniczkujący Transmitancja układu różniczkującego dana jest w postaci $T(s)=ks$ Układ nosi nazwę różniczkującego, gdyż operator s w dziedzinie częstotliwości zespolonej oznacza różniczkowanie funkcji w dziedzinie czasu. Charakterystyka częstotliwościowa opisana jest zależnością $T(j\omega )=kj\omega =k\omega e^{j90^{\circ }}$ Charakterystyka amplitudowa jest funkcją liniową $|T(j\omega )|=k\omega$ a charakterystyka fazowa stała, niezależnie od częstotliwości $\phi (\omega )=90^{\circ }$ Wykres obu charakterystyk układu różniczkującego przy k>0 przedstawiono na slajdzie 14.

---

Przesuwnik fazowy Przesuwnik fazowy jest układem przesuwającym fazę napięcia wyjściowego względem wejściowego bez zmiany amplitudy sygnału. Transmitancję przesuwnika fazowego określa zależność $T(s)=\frac{-s+a}{s+a}$ Charakterystyka częstotliwościowa przesuwnika określona jest następującą relacją $T(j\omega )=\frac{-j\omega +a}{j\omega +a}=\frac{\sqrt{{\omega }^2+a^2}}{\sqrt{{\omega }^2+a^2}}\cdot \frac{e^{-j\varphi (\omega )}}{e^{j\varphi (\omega )}}=$ $=1e^{-j2\varphi (\omega )}$ gdzie kąt $\varphi (\omega )$ określony jest wzorem $\varphi (\omega )=arctg(\frac{\omega }{a})$. Powyższa zależność potwierdza, że przesuwnik fazowy nie zmienia amplitudy sygnału wejściowego $(|T(j\omega )|=1)$ a wpływa jedynie na przesunięcie fazowe między sygnałem wejściowym i wyjściowym. Charakterystyka fazowa przesuwnika określona jest zależnością $\phi (\omega )=-2arctg(\frac{\omega }{a})$ Na slajdzie 15 przedstawiono wykres charakterystyki fazowej przesuwnika o transmitancji ze slajdu 6 w funkcji pulsacji dla wartości a=1. Przesunięcie fazowe układu jest funkcją częstotliwości i zmienia się od zera do wartości . Wartość przesunięcia fazowego dla konkretnej wartości częstotliwości można regulować poprzez zmianę współczynnika a transmitancji. Na rys. poniższym przedstawiono wykres przedstawiający zmianę kąta przesunięcia fazowego układu dla pulsacji jednostkowej przy zmianie wartości współczynnika a.

---

Charakterystyki częstotliwościowe układu n-tego rzędu Najbardziej ogólnym przypadkiem jest układ opisany transmitancją operatorową T(s) n-tego rzędu o postaci ogólnej zadanej wzorem